坦克炮塔转动惯量测量方案设计
徐 静,门义双
(中国北方车辆研究所,北京 100072)
炮塔是一种固定在坦克、装甲车上的射击武器装置,炮塔性能的高低对于常规武器及高射炮的射击效率和精度有重要影响[1].在炮控系统的总体设计中,炮塔转动惯量是火炮随动系统的一个基本参数,其值的变化会改变速度控制的模型,降低炮控系统的速度响应特性从而影响整个系统的机械特性[2-3].在设计炮塔电动机参数时,需要考虑到电动机的最大输出功率、输出扭矩能否满足高速调炮与低速瞄准的要求.而炮塔转动惯量及转动时的角加速度决定了电机输出扭矩的大小.因此快速精确地测量自行火炮及坦克炮塔绕其回转中心的转动惯量是设计高性能炮控系统的重要前提条件.
传统测量坦克炮塔转动惯量的方法主要有两种.一是对炮塔及其各部件进行建模和有限元仿真计算.这需要十分准确、完善的炮塔及其上安装部件的模型,转动惯量计算值的准确度受模型准确性的影响.二是建立炮塔转动惯量试验测试平台.根据刚体摆动周期与惯量之间的关系计算,如扭振法、滚摆法和落体法.文献[4]给出了一种由炮塔、身管、弹簧、加速度传感器和记录仪器组成的炮塔转动惯量试验测试装置.通过测量炮口振动周期,来计算炮塔转动惯量[4].这种方法需要特殊试验平台,测量精度低,不能利用炮控系统自身部件快速反映炮塔转动惯量的变化.
基于电机驱动炮控系统的坦克炮塔转动惯量测量方案,从刚体的定轴转动定律和电机电流扭矩特性出发,推导炮塔转动惯量的理论计算公式.在测定炮塔电机特性基础上,利用炮控系统中的陀螺仪传感器和数据采集系统同步采集炮塔的角速度与电机电流数据,经数据处理得到炮塔转动的扭矩和角加速度,进而计算出炮塔转动惯量.
1 坦克炮塔转动惯量测量原理
炮塔电动机驱动坦克炮塔运动结构框图如图1所示,其中工作机构代表炮塔体和火炮,炮塔电动机的减速装置为方向机.实时测量得到的炮塔转动惯量为方向机、炮塔体和火炮相对转轴的转动惯量.
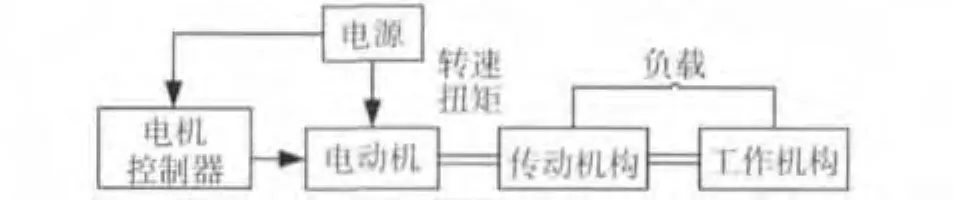
图1 电机驱动炮塔结构框图
考虑电动机的外特性,以直流电机为例,输出扭矩与电枢电流之间关系为[5]
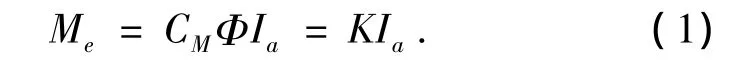
式中:CM为扭矩系数;Φ为主磁通;Ia为电枢电流;K是电流扭矩系数.
炮塔运动系统示意图如图2所示.它包含水平向电机驱动炮塔体在水平向的旋转运动如图2(a)所示,和垂直向电机驱动火炮在垂直向的运动如图 2(b)所示[6].
图2中炮塔水平向旋转运动的中心为O1,火炮垂直向旋转中心为O2,且O1O2=d;炮塔体质量为m1,火炮质量为m2,长度为L.当炮塔水平旋转时,火炮垂直向的运动对系统将产生负载惯量扰动.假设炮塔体形状相当规则,其等效半径为r,火炮密度均匀,火炮炮管轴线与水平面夹角为β.那么炮塔体和火炮对于旋转中心O1的转动惯量为
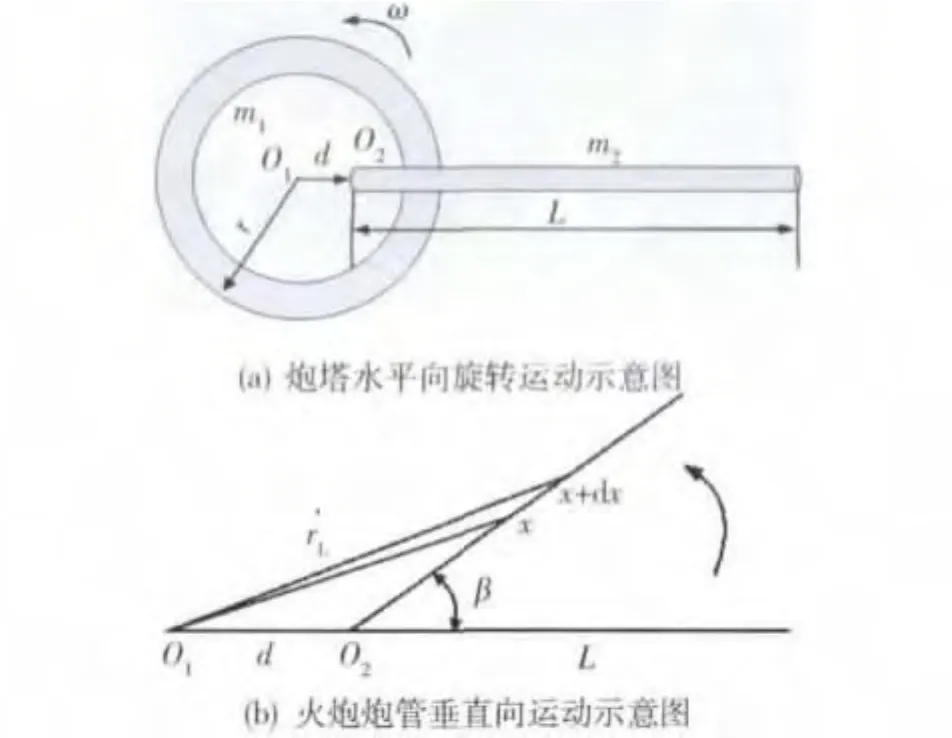
图2 炮塔运动系统示意图
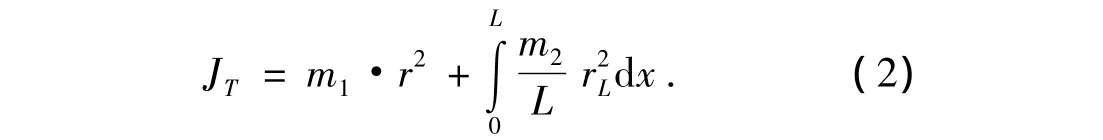
据图2(b)有
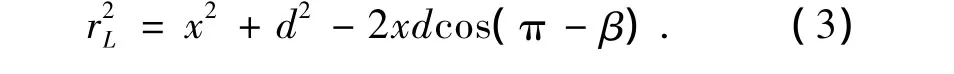
将式(3)代入式(2)得
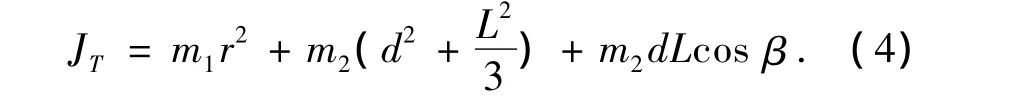
实际炮塔在运动过程中,炮塔座圈并非绝对水平,存在一定的倾斜角度,设为θ,且规定炮塔顺时针旋转时θ取值为正.因此炮塔在转动过程中存在偏心矩,偏心矩的数值与炮塔质心位置有关,假设方位向旋转中心O1与炮塔质心O3之间距离为dθ. 则偏心矩为
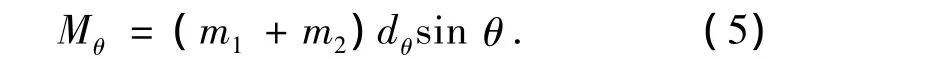
炮塔在旋转过程中同时存在摩擦力矩.设旋转时的摩擦系数为f,炮塔水平向旋转角速度为ω.则摩擦力矩Mf为

根据动力学原理得炮塔运动微分方程
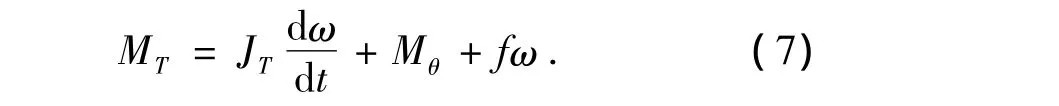
式中:MT为炮塔的扭矩;JT为炮塔的转动惯量.

图3 电机驱动炮塔系统扭矩关系图
炮塔电动机驱动炮塔运动时的扭矩关系如图3所示,Me为电机扭矩,M0为等效电机摩擦力矩,ZT和Z分别表示炮塔和电机的等效齿轮齿数,JL为炮塔等效到电机一侧的转动惯量.
忽略传动机构的齿侧隙因素,根据式(7)和图3得到系统的扭矩微分方程
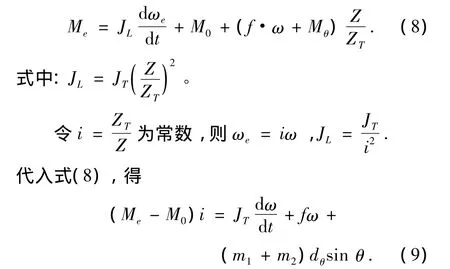
将炮塔台架调至近似水平状态,操纵炮塔电机驱动炮塔顺时针及逆时针方向各旋转一定的角度.电机扭矩分别为Me1和Me2,炮塔角速度分别为ω1和ω2,则式(9)可写成
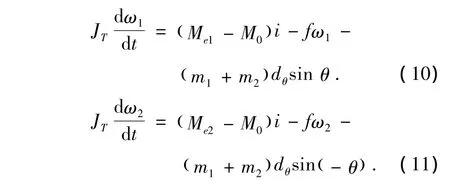
将式(10)与式(11)求和,得到炮塔转动惯量的理论计算公式
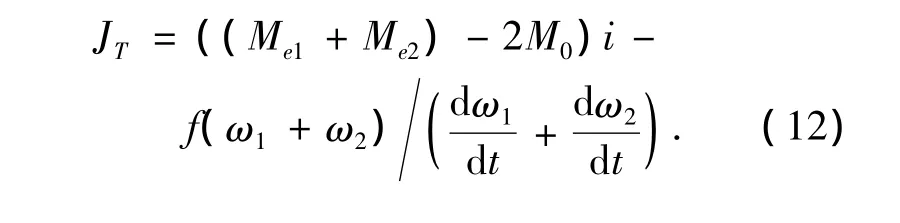
2 炮塔转动惯量试验测定方案
炮塔转动惯量的测量装置包含两套检测台架与数据采集分析系统.一是电机转速扭矩检测系统;二是炮塔转动角速度和电机电流的动态同步测量系统.
2.1 炮塔电机特性测定方案
炮塔电动机是炮控系统的核心驱动部件.要准确获取炮塔的相关参数,需要精确测量驱动炮塔的电机自身的特性.电机的输出扭矩与电流特性通过电机转速扭矩检测台架 (如图4所示)试验获得.
电机检测台架是一种机电混合台架即混合惯量模拟台架[7].通过电机码盘与转速扭矩传感器及外围数据采集电路,测定电机的输出扭矩与电流之间的特性关系.图4中机电混合检测台架的动力学模型为
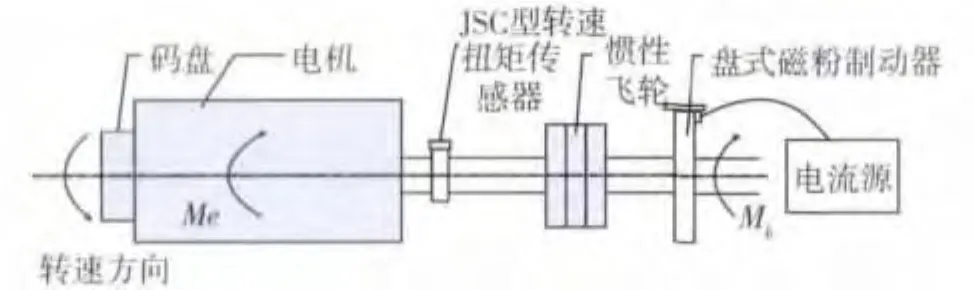
图4 电机检测台架结构框图

式中:J0为检测台架的转动惯量和;ε为电流源提供制动力矩时台架角加速度;Mb为制动力矩.
为使传感器正常工作且能实时采集出电机电流及码盘和传感器的输出信号,设计了与之配套的供电电源与数据采集电路板,以便精确拟合电机的输出扭矩和电流特性曲线.数据采集电路以TMS320F2808芯片为主控CPU,硬件系统由DSP及其外围电路、电源转换电路、电流采集及A/D转换电路、输入信号电平转换电路、串口和CAN口电路组成.其组成原理框图如图5所示.
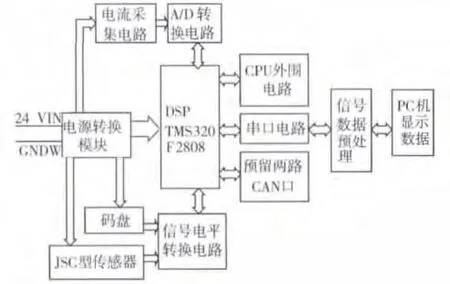
图5 硬件实现原理框图
2.2 炮塔角速度和电机电流的动态同步测量方案
对于中空大回转体转动角速度的测量,工业上主要的方法有:机械测角方法、电磁测角方法、光学测角方法以及光电测角方法,等等.通过采集数据再经后处理得到系统的角速度[8].
炮塔转动角速度和电机电流的动态同步测量系统是利用炮控系统中的陀螺仪、电机驱动器等部件和与之配套的数据采集系统采集炮塔的角速度和电机电流数据,从而获得炮塔电机的输出扭矩和炮塔转动角加速度的同步信息.炮塔转动角速度和电机电流的动态同步测量方案为:在坦克炮塔上安装一个惯性角速度敏感器件——高精度光纤陀螺仪传感器,利用炮塔电机驱动器中的LEM块,以DSP为核心处理器件,同时采集炮塔角速度和电机电流的离散数据并储存.通过适当的数据处理,选择合适的滤波算法、差分计算求出对应的角加速度及电机输出扭矩.光纤陀螺仪传感器与LEM块采集到的数据通过数字通讯接口与上位机连接并显示,系统设计中采用CAN总线方式传输数据,通过软件设定数据采集周期.
炮塔转动角速度及电枢电流同步采集系统原理框图如图6所示.该系统设计采用的测角速度方案,能够克服炮塔齿圈加工等因素导致的误差,实现炮塔转动角速度的高精度测量.
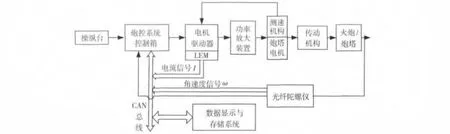
图6 炮塔角速度及电机电流采集系统原理框图
3 炮塔转动惯量试验测量结果
利用电机转速扭矩检测系统试验测得某一炮塔电机的输出扭矩与电流特性.其关系如式(14)所示.
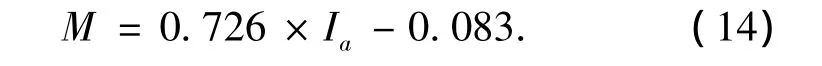
式中:M=Me-M0.
利用炮塔角速度和电机电流动态同步测量系统,采集ω与I数据.其采样间隔ΔT=2.1 ms,角速度的单位为0.002(o)/s,电枢电流的单位为0.01 A.炮塔与电机齿轮传动比i=550.取θ=0,忽略炮塔摩擦力矩.以输入正弦激励信号为例,其响应水平角速度和水平电流曲线如图7所示.
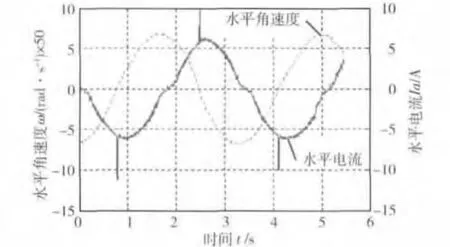
图7 正弦激励下炮塔水平角速度和电流曲线
由于光纤陀螺自身特性,采集到的炮塔角速度与电流数据量庞大且存在噪声,因此需要进行一定的数据分析与剔除野值、滤波等处理.滤波后得到曲线如图8所示,差分后得到炮塔角加速度与电机输出扭矩曲线如图9所示.
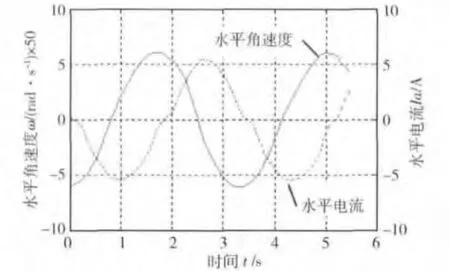
图8 滤波后炮塔水平角速度和电流曲线
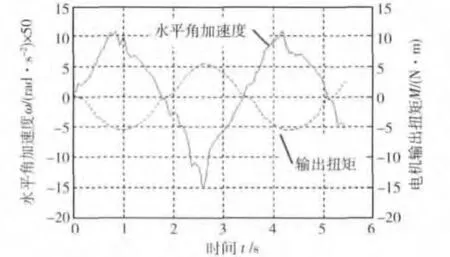
图9 炮塔水平角加速度和电机扭矩曲线
从图9中,取对应时刻下炮塔角加速度和电机输出扭矩值,根据式(15)计算炮塔转动惯量.
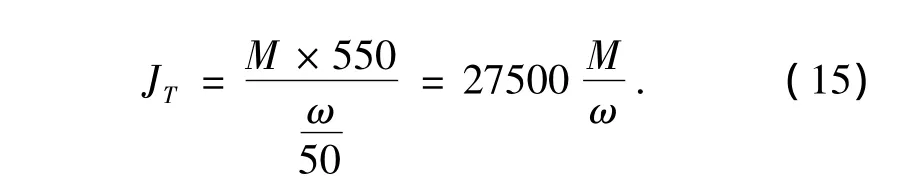
每间隔10 ms取值计算,得到转动惯量取值范围为16216~20473 kg·m2.设
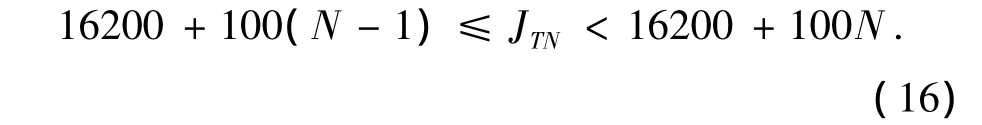
式中:N=1,2,…,n.XN为JTN的取值个数,全部取值点数为X,令xN=,则xN~N的关系作为炮塔转动惯量的概率密度函数,其曲线为近似正态分布曲线,如图10所示.
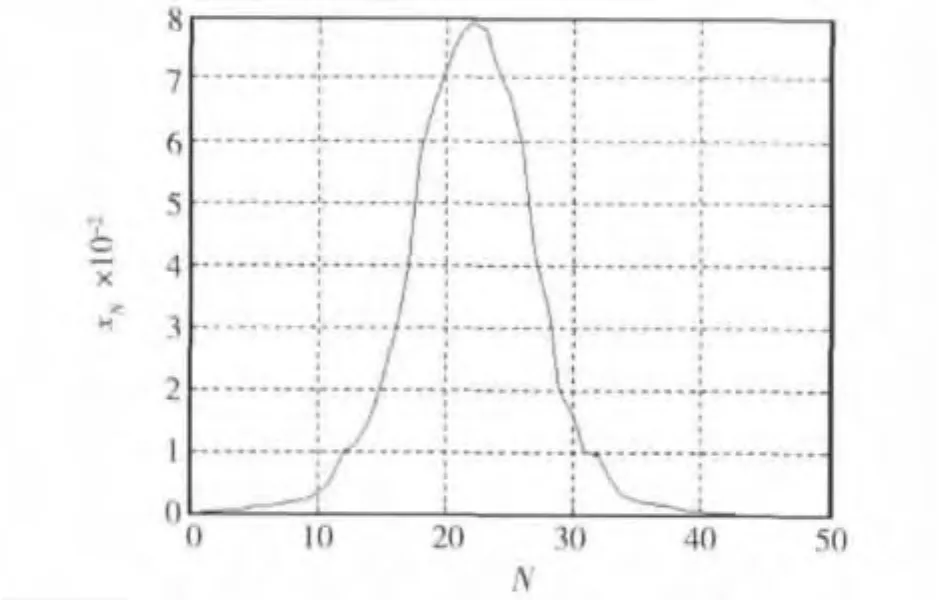
图10 炮塔转动惯量计算值概率密度分布曲线
根据图10,得xN~N(23,5.2132).故炮塔转动惯量为JT23.根据式(17),取N=23时计算的平均值为试验得到的炮塔转动惯量.
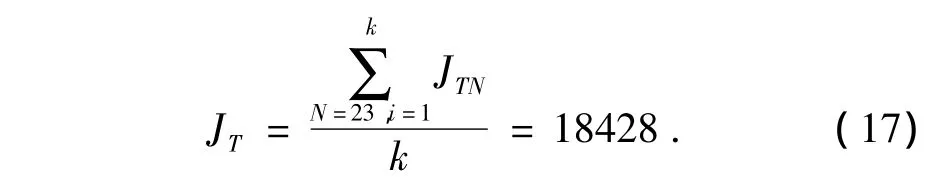
炮塔转动惯量的最大相对误差为
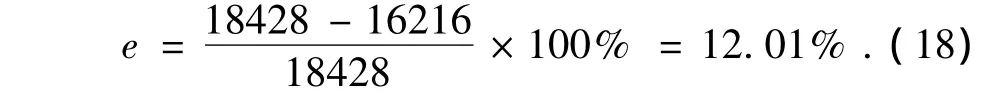
试验测量计算得到炮塔的转动惯量为18428 kg·m2,相对误差为12.01%,精度较高.可以作为炮控系统总体设计时的炮塔转动惯量参考值.
4 结论
针对炮控系统总体设计时对炮塔转动惯量的定量需求,设计出一套测定坦克炮塔转动惯量的方案.该方案较传统方法提高了测量精度,并且能快速地反映炮塔转动惯量的变化,有利于对火炮随动系统的速度响应环进行精确的控制.
由于试验中采集的数据量庞大,因此为了更加准确地计算出炮塔转动惯量,不仅需要对传感器采集的数据做进一步的分析与处理,还要考虑炮塔旋转过程中的摩擦力矩.由于实际炮塔转动惯量的真实值无法确知,所以在之后的试验中,通过对炮塔在不同旋转工况下的转动惯量的测量值进行比较,进一步证明利用此方案测得的炮塔转动惯量数值是准确的.
[1]杜春江,钱林方,徐亚栋,等.炮塔体结构分析与优化 [J].系统仿真学报,2009,(15):4899-4902.
[2]JunggiLee,Jinseok Hong,Kwanghee Nam,et al.Sensorless control of surface-mount permanent magnet synchronous motors based on a nonlinear observer [J].IEEE Transactions on Power Electronics,2010,25(2):290-297.
[3]Piippo A,Hink kanen M,Luomi J,et al.Analysis of an adaptive observer for sensorless control of interior permanent magnet synchronous motors[J].IEEE Transactions on Industrial Electronics,2008,55(2):570-576.
[4]王宝元.炮塔转动惯量实验测试装置 .中国,00262463.X [P],2002-07-03.
[5]杨 耕,罗应立.电机与运动控制系统 [M].北京:清华大学出版社,2006.
[6]汪正军,王军政,马立玲.大惯量随动系统解析模型预测控制 [J].北京理工大学学报,2011,31(11):1307-1312.
[7]林巨广,苏晓峰,丁苏赤.混合惯量模拟试验台架设计方法的研究 [J].设计与研究,2009,(11):35-36.
[8]徐建华.低成本高精度角位移测量系统研究与设计[D].太原:中北大学,2008.

