基于市场机制的多项目分散式调度问题

王 磊，战德臣，聂兰顺

（1.哈尔滨工业大学 计算机科学与技术学院，黑龙江 哈尔滨 150001；2.中国科学院 苏州生物医学工程技术研究所，江苏 苏州 215163）

0 引言

多项目环境下并行的多个项目通过共享资源形成竞争合作关系，多个局部决策问题（项目调度）互相耦合、互相约束。传统的“基于掌控全局信息集中优化”的多项目调度方法一般通过超网络图的方式建模，基于事先已知的项目优先级对多项目资源的争用冲突进行协调。一方面，多个项目的局部决策问题已是难解的组合优化问题，且局部决策问题在决策目标、决策内容、决策模型等方面可能具有较大的异构性；另一方面，局部决策之间的依赖关系多样，具有时间、数量、价格等多维性，对于事先无法判断项目优先级或者预判优先级的准确性和合理性有待商榷的问题，集中式解法难以进行合理有效地协调。

Confessore等［1］建立了一种基于多智能体系统（Multi-Agent System，MAS）的分散式资源受限多项目调度问题模型，通过封装的多个调度Agent对每个项目进行计划和调度，并采用迭代组合拍卖机制解决多项目之间争用共享资源的冲突问题。经过计算分析，该模型能够解决包含最多5个项目、每个项目包含最多8 个任务的多项目调度问题。Homberger［2］研究了包含多种共享资源的分散式多项目调度问题，通过统一协调的分散式解法对问题进行求解，在迭代过程中采用重启进化策略（Restart Evolution Strategy，RES）解决单一项目的调度问题。构造了80个大规模多项目调度问题实例，其中每个实例可以最多包含20个项目，每个项目可以包含120个任务。通过比较集中式解法与分散式解法，证明MAS模型和分散式解法更适用于解决多项目调度问题，同时RES能够较好地解决单一项目的资源受限项目调度问题（Resource Constrained Project Scheduling Problem，RCPSP）。Lau 等［3］建立的用于求解分散式项目调度问题的MAS模型中，包含一组调度Agent和一组针对不同局部优化目标的承包商或资源Agent，并提出基于讨论协商的协调机制。通过多个Agent之间交换附加信息的手段提高算法的收敛速度和求解质量，并验证了这种协商机制能够有效解决项目数量较少的多项目调度问题。Lee等［4］采用基于市场机制的组合拍卖求解分散式项目调度问题，比较了集中式和分散式两种决策方式的求解效果，并验证了拍卖机制能够有效地解决项目数量较少的问题。应瑛等［5］采用组合拍卖机制对资源受限多项目调度问题进行研究，通过逐步调节不同资源在不同时段的价格，引导各个项目更加合理地利用不同时段的资源，实现资源受限多项目调度问题的整体优化。Arauzo等［6］提出基于拉格朗日分解的组合拍卖机制，用以解决多项目环境下的资源分配问题。

本文在考虑工期弹性的项目工期优化方法前序工作的基础上［7］，进一步探讨在最短工期和交货期之间寻找成本最小的最佳工期的合理性与现实意义，并推广到多项目工期优化与协调问题领域，针对集中式方法难以求解的优先级未知多项目调度问题，采用项目各自分散式调整弹性任务来优化项目工期、多个项目通过对共享资源竞价与拍卖品价格迭代调整的方式，借助市场机制和竞争判优实现多项目资源的竞争冲突消解，以及多项目距离理论最佳工期的平均差距减小的协调优化效果。最后通过一系列实验与结果分析，对项目计划工期的寻优效果、多项目平均工期差距、多项目平均相对差距、弹性工期对结果的影响，以及市场竞争判优方式对多项目的协调效果等方面的性能进行评价，探讨分散式解法相比集中式解法的优势与适用性。

1 分散式决策的多项目调度问题

多项目调度问题主要解决多个项目针对各自任务的排序与局部资源分配问题，以及多项目对共享资源争用的协调与分配问题。图1所示为基于分散式调度与市场竞争协调的多项目调度协调方法，该方法将项目调度与协调决策有机结合，在充分发挥多项目分散式独立决策、利用任务弹性寻找各自项目最佳工期的基础上，借助市场机制协调多项目对共享资源的争用冲突。

多项目计划中，一味压缩工期并非是最好的，由于受上级计划（订单接受决策）确定的工期底限约束，提前完工可能会导致出现以下情况：①继续占用空间资源产生成本；②移出空间资源产生库存成本或者提前交货的惩罚；③压缩工期可能需要使用更多的协作厂资源而产生更多的租用成本。因此需要寻找满足工期底限的、以项目成本最小为目标的最佳工期。某些大型装备制造企业（如造船企业）的任务存在工期刚性／弹性，可以通过调整弹性任务工期确定刚性任务时间。项目总成本包括固定资源（空间资源+可更新资源）和租用资源（协作厂的可更新资源）产生的成本，而且计算方式不同：①空间资源成本随占用时间线性单调递增，在工期底限之前将中间产品移出空间资源，一般不会减小成本（空间资源空置同样产生成本）；②总装企业的可更新资源单位时间成本相对较低，协作厂的租用资源成本相对较高，而且会根据竞争情况出现波动。由此得出资源使用策略：充分利用工期底限确定的空间资源占用时长和因租用资源，尽量少用存在冲突而价格提高的竞争资源。

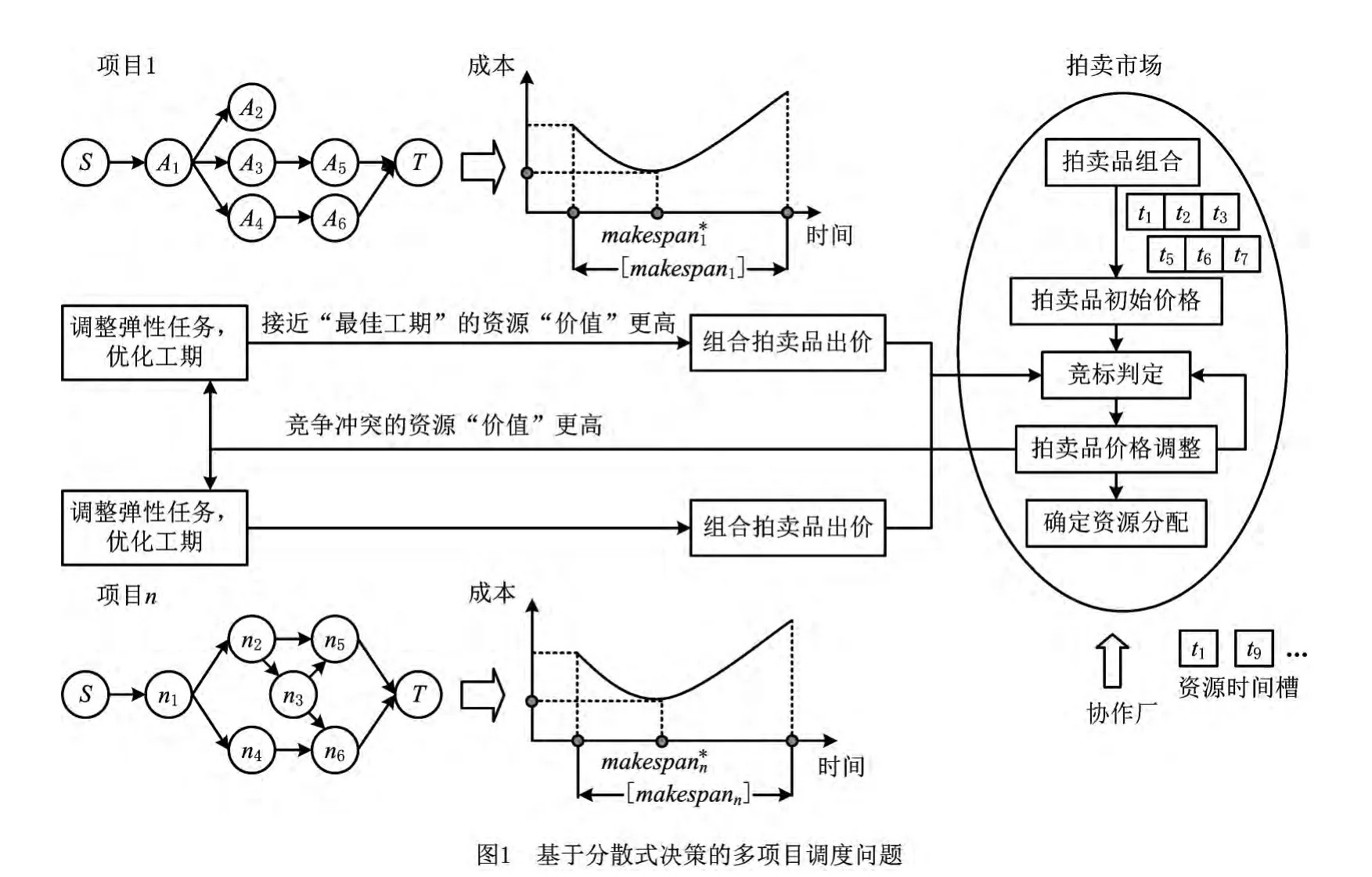
首先以满足工期底限为约束条件，随机选择一种弹性任务工期设置和任务时间安排方案进行初始调度。然后在弹性任务的邻域结构中搜索其他可行解，寻找项目成本最小的工期确定为最佳工期，采用禁忌搜索策略避免搜索过程陷入局部最优解。再次进入多项目协调过程，每个项目根据最佳工期和相应的任务安排提出共享资源需求的初始竞价（保留价格），即需要哪个时段、哪种类型的资源和数量。因为任务的资源需求具有互补性和替代性，所以采用组合拍卖品模型。汇总多项目提出的资源竞价，通过竞争判优进行协调与分配：如果提出的共享资源竞价不存在时间、种类或数量冲突，则认为多项目都实现了（接近）各自的最佳工期，调度结束并分配资源；当某个时段的资源竞争存在冲突时，本轮不分配该资源，而是以保留价格为基础调整（提高）该时段资源（拍卖品）的价格，并将调整信息反馈给相应的项目。多项目根据调整的资源价格重新优化工期与任务安排，迭代竞标：以最佳工期确定的弹性任务工期与任务安排为搜索原点进行基于禁忌搜索的寻优，按照最佳工期寻优过程中对空间资源、总装企业和协作厂的可更新资源及成本的分析，寻找接近最佳工期的项目成本较小的另一种弹性任务工期调整和任务安排方案。根据新的弹性工期调整方案和项目任务安排方案，对需要的资源种类、数量、时段提出新的资源竞价。如此迭代，实现以平均项目工期优化差距最小为目标的分散式多项目调度协调过程。

2 基于MAS的多项目调度模型

基于分散式决策方式求解的多项目调度模型包括多个项目的局部决策模型以及相互之间的协调决策模型，经过迭代式调整最终实现多项目调度协调优化，得到每个项目的任务时间安排以及局部资源和共享资源的分配方案。如图2所示为基于MAS的分散式多项目调度模型框架，包括每个项目调度的局部决策以及解决共享资源争用协调的协调决策。

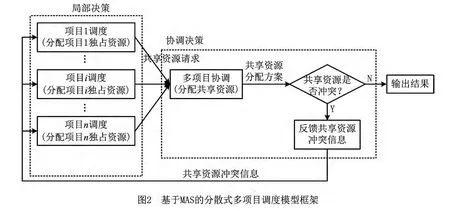
定义1 局部决策。各个项目经理掌握自身的项目信息，决定项目所有任务的开始／完成时间，分配项目的独占资源，从而达到某项决策目标的决策过程，称为局部决策。

假设：项目i的交货期为，拖期惩罚因子为εi，包含ni项任务，任务执行阶段不可中断，项目i中所有任务的时序关系已确定并记为Ai；项目i占用si种项目独占资源Ri，资源hi∈Ri在每个时段的可用量均为ρhi；任务ji需要rjihi单位的项目独占资源hi，所需数量0≤rjihi≤ρhi；项目i的项目经理负责决定本项目所有任务ji∈Ji的计划开始时间sji、计划完成时间fji以及项目独占资源Ri的分配方案；任务ji的执行时间dji=fji-sji，项目计划时段上限为T，所有在时段t=｛1，2，…，T｝执行的任务集合记为It；参数dji，ρhi和rjihi均为非负实数。项目局部决策的决策目标为满足任务时序约束和项目独占资源约束下完成项目的所有任务并实现某项性能的优化，如项目工期最短、项目成本最小等。项目i的局部决策结果为项目i的调度Si，Si=｛sj1，sj2，…，sjni｝。

定义2 协调决策。协调机制掌握共享资源信息并决定共享资源的分配方案，协调多个项目，从而达到某项决策目标的决策过程，称为协调决策。

假设：z个项目需要调度，表示为集合P=｛1，2，…，z｝；所有项目共享种共享资源，资源在每个时段的可用量为ρk；项目i的任务ji需要rjik单位的共享资源k，所需数量0≤rjik≤ρk；参数ρk和rjik均为非负实数；协调者或者某种机制确定共享资源的分配方案，消解可能存在的多项目争用共享资源的冲突；多项目全局决策的目标为共享资源约束下完成所有项目的任务并实现某项性能的优化，如所有项目总工期最短、所有项目总成本最小等；多项目全局决策的结果为多项目调度S，S=｛S1，S2，…，Sz｝。

在以上对项目局部决策和多项目协调决策定义的基础上，多项目分散式调度问题可以描述为：如果多个项目通过共享资源发生联系，并且多项目调度的决策结构是分散的，即每个项目通过项目经理进行局部决策确定本项目所有任务的开始／完成时间并分配项目独占资源，多个项目通过协调者或者某种机制进行协调决策分配共享资源，从而对多个项目分散的局部决策结果进行协调。本文封装以下Agent并建立调度决策模型。

（1）项目Agent

项目Agent负责管理一个项目的所有任务，完成该项目的局部决策。项目经理掌握本项目的任务工期估计值、任务所需要的资源种类和数量，以及反映任务时序关系的任务网络图等信息，在任务时序关系约束和项目独占资源可用量等约束条件下，安排本项目所有任务的开始／结束时间，确定独占资源的分配方案。如果以项目成本最小为决策目标，则项目Agent进行局部决策的概念性数学模型如下：

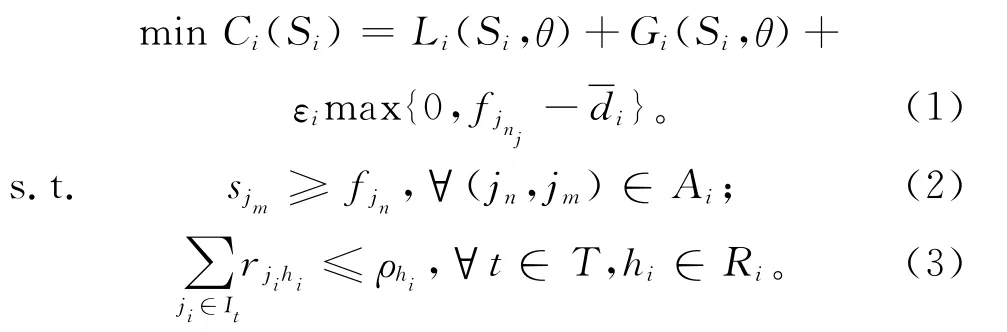
式（1）表示项目i的成本最小，其中Li（Si，θ）=表示项目i的局部资源使用成本，θhit表示资源hi∈Ri在时段t的使用成本，Gi（Si，θ）表示项目i的共享资源使用成本，εimax｛0，fjnj-di｝表示项目i的拖期惩罚，εi表示项目i的拖期惩罚因子；式（2）表示项目i的所有任务均满足时序关系约束；式（3）表示项目i在任意时段执行任务的独占资源使用量总和不多于该项目的独占资源可用量。

（2）协调Agent

协调Agent负责多项目协调决策，协调多个项目分散的局部决策结果，确定共享资源的分派方案。如果以所有项目总成本最小为决策目标，则协调Agent的概念性数学模型如下：

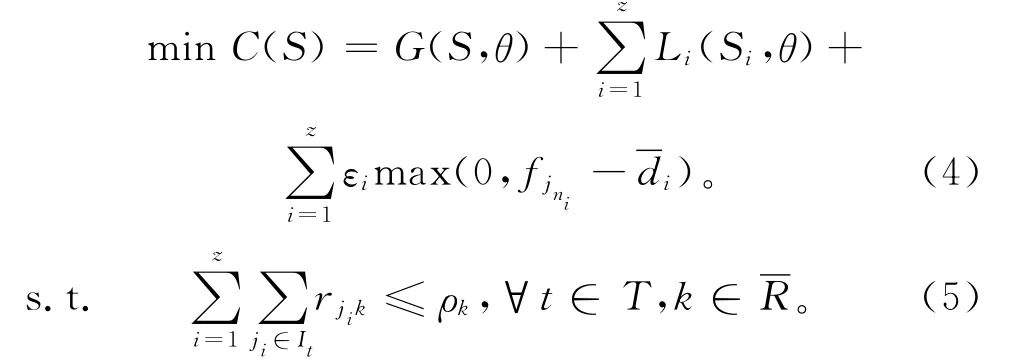
式（4）表示所有项目的总成本最小，其中G（S，θ）表示共享资源使用成本，表示所有项目的项目独占资源使用成本之和，表示所有项目的拖期惩罚之和；式（5）表示所有项目在任意时段执行任务的共享资源使用量总和不多于共享资源可用量。

3 基于市场机制的分散式项目调度方法

3.1 基于组合拍卖的市场竞争机制

在基于市场机制的分散式项目调度求解过程中，将项目Agent视为竞买者，协调Agent视为拍卖者，资源使用权视为拍卖品。每一个竞买者和拍卖者都有各自的利益目标，竞买者在文献［7］提出的项目工期优化方法指导下希望实现自身的最佳工期，因此对相应的共享资源提出需求和竞价；拍卖者希望共享资源得到有效分配，以减少多个项目的总成本。因为任务可能需要获得多种资源之后才能执行，所以采用组合拍卖的方式，在每轮拍卖中竞买者对需要的拍卖品组合提出竞价，拍卖者确定获胜者并调整拍卖品价格，没有完成拍卖的竞买者和拍卖品进行下一轮拍卖，通过这种迭代组合拍卖逐步寻找最优的资源配置方案，最终达到多个项目分散的局部决策的协调，使得所有项目均接近各自的最佳工期。

将一个单位的共享资源k在时段t的使用权μkt看作一项独立的拍卖品，即资源时间槽（resource time slot），共存在项单项拍卖品，组成拍卖品集合，其中：为共享资源种类，T为计划时段上限。如果项目i的任务ji执行期间需要rjik1单位的共享资源k1和rjik2单位的共享资源k2，则该任务需要得到拍卖品组合Gji=｛μkut｜rjiku＞0，sji≤t≤fji｝才能得以执行，并且ku=｛k1，k2｝。项目i需要得到拍卖品组合Gji才能保证所有任务ji∈Ji执行，所有项目都得到需要的拍卖品组合才能执行。

组合拍卖过程包括竞买者竞价和拍卖者调整价格两个主要过程，该方法通过拍卖品价格的迭代调整来最终获得全局优化效果。首先，竞买者竞价解决各个项目的局部决策问题，为自身项目的所有任务安排开始／结束时间、分配项目独占资源，并提出共享资源请求；然后，进行多项目全局决策（即拍卖者调整价格过程），汇总本轮多项目分散决策产生的共享资源，请求判断是否存在共享资源冲突，针对存在冲突的资源时间槽调整价格，在下一轮拍卖中要求相应的竞买者继续竞价，如此迭代，直到多项目不存在共享资源争用冲突。组合拍卖过程如图3所示。

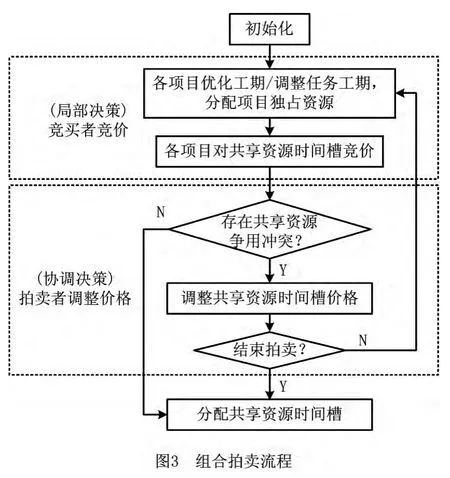
从组合拍卖流程可以看出，竞买者竞价与拍卖者调整价格两个阶段分别对应多项目分散式局部优化和协调过程，在本文研究中前者采用文献［7］提出的面向项目成本的工期优化方法，对不同时段的资源时间槽提出竞价，后者采用本文提出的价格调整方法和竞争判优方式，协调多项目对相同资源时间槽的争用冲突。

3.2 分散式优化与竞买者竞价

组合拍卖过程中竞买者i表示项目经理i∈｛1，2，…，z｝，在拍卖过程中对拍卖品（资源时间槽）组合提出竞价。在第v轮拍卖中，竞买者i出价，用二元组表示。其中：表示提出的竞价；表示竞标的拍卖品组合且≥0，表示需要共享资源k的数量。

θkt表示拍卖品μkt的当前价格，即资源k在时段t的价格，项目i在当前给定资源价格下的总成本为Ci（Si）=Li（Si，θ）+Gi（Si，θ）+εimax｛0，表示项目i的独占资源使用成本，表示项目i的共享资源使用成本，εimax（0，fji-di）表示项目i的拖期惩罚。

本文采用基于弹性工期调整的禁忌搜索算法进行项目工期优化，根据各个项目更为需要的资源时间槽确定竞价。禁忌搜索算法是基于扩展局部邻域搜索的一种元启发式算法，通过人工智能的方法进行全局逐步寻优，可以较好地模拟计划人员在任务时序约束、资源约束等条件下逐步寻求最优计划的过程。禁忌搜索算法通过引入一个灵活的存储结构和相应的禁忌准则来避免迂回搜索，并通过藐视准则赦免一些被禁忌的优良状态，进而保证多样化的有效搜索，最终实现全局优化。

禁忌搜索算法的几项要素设计如下：

（1）初始解 在不考虑资源约束的条件下，采用关键路径法计算项目i的调度si，如果任务jni的完成时间不晚于项目交货期，则si为初始解。

（2）邻域映射结构 选择独占资源使用率最高的时段，将该时段任意一项任务的开始时间提前或者推后一个时间单位。

（3）藐视规则 如果某个状态的性能优于当前的最优状态，即某种调度方案下的项目成本比当前解对应的项目成本更小，则无视其禁忌属性，直接选取它作为当前状态。

（4）终止条件 任务jni的完成时间大于或等于项目交货期，或者迭代次数等于100。

3.3 拍卖者调整价格

所有竞买者提出的竞价汇集到拍卖者处，拍卖者判断该轮拍卖的获胜者，并根据竞买者提出的竞价对拍卖品价格进行调整，使得能够以更高的价格卖出所有的拍卖品。获胜者确定问题（Winner Determination Problem，WDP）是组合拍卖的核心问题，属于NP-complete 问题。白鉴聪等［8］对基于OR 与XOR 标集的WDP 问题建立了0-1 规划模型，并提出免疫算子与单亲算子相结合的启发式算法；金涬等［9］提出物品分配方案的k-UNT 条件，并给出了一种基于1-UNT 检查的求边际效用递减组合拍卖的近似算法。本文主要对拍卖者价格调整策略进行研究与设计。

假设所有拍卖品都有保留价格，即拍卖品不能低于此价格出卖，记为，第一轮拍卖时所有的拍卖品组合价格为p1（μkt）=。pv（μkt）为拍卖品组合μkt在第v轮拍卖时的价格。在第v轮拍卖结束后拍卖者根据所有竞买者的竞价判断是否存在资源冲突，即是否存在某个时段竞买者对某种资源的需求量超出了资源可用量，如果存在资源冲突需要进行下一轮拍卖，则拍卖者需要确定v+1轮拍卖中拍卖品μkt的价格pv+1（μkt）。拍卖者一般采用提高拍卖品价格的方式要求竞买者重新竞价，迫使相应的竞买者调整自身的局部决策方案，从而放弃该项拍卖品而竞标其他拍卖品，最终达到多项目共享资源冲突消解的目标。可以采用式（6）进行价格调整：

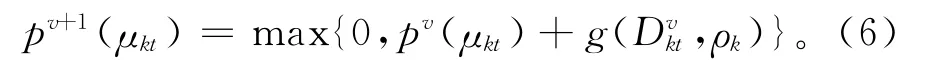
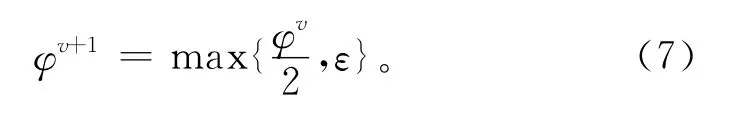
这种价格调整方式可以保证在拍卖过程的初期能够根据资源的需求情况进行较大幅度的价格调整，在拍卖后期对资源价格进行微调，以实现资源的最优配置。因为拍卖品组合μkt的价格不能低于其子集μ′kt，μ′kt⊆μkt的价格，所以确定pv+1（μkt）还需要满足

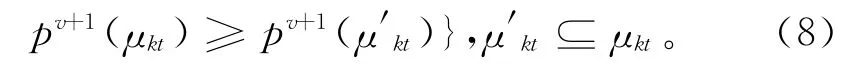
4 数值实例实验与分析

为了验证本文提出的分散式项目调度协调方法对求解考虑工期弹性的多项目调度问题的性能，设计了数值实例并进行仿真实验，通过与集中解法进行比较，从解法对项目最佳工期的寻优效果、多项目平均工期差距、多项目平均相对差距、弹性工期对结果的影响，以及市场竞争判优方式对多项目的协调效果等方面进行分析，探讨分散式方法相比集中式解法的优势与局限性。

4.1 测试算例参数设置

采用Kolisch等［10］设计的项目调度问题测试集生成工具ProGen构造问题测试集，测试集的主要参数及含义如表1所示。

根据前文的分析探讨，每个项目存在最佳工期与计划工期，而在并行多项目争用资源环境的情况下，不能达到所有项目的计划工期均为最佳工期，因此通过考察多个项目计划工期相对于最佳工期的平均差距，可以体现方法的协调优化效果。

为了比较分散式解法与集中式解法对本文所研究的多项目调度协调问题的优化效果，采用Pro-Gen，分别设置项目数为3和5，每个项目的最大任务数分别为10和18，其中弹性工期任务占总任务数的40%，共享资源种类分别为1，2和3，对每个问题随机生成测试实例，对这12组实例分别采用本文算法以及Peteghem 等［11］提出的求解多模式项目调度问题的双种群遗传算法（集中解法）进行比较，采用禁忌搜索算法分别计算每个项目不考虑其他项目争用共享资源的项目最佳工期，采用不同方法分别计算每个项目的计划工期，采用平均工期差距=（计划工期i-最佳工期i））／z计算结果与项目最佳工期的平均相差天数，采用平均相对差距=（计划工期i-最佳工期i）／最佳工期i）／z）×100%计算不同方法求解的平均相对差距，从而表征计算结果与单项目最佳工期的平均差距。计算过程均采用MATLAB 7.0编程实现，运行环境为Pentium（R）4，CPU 主频为3.00GHz，1.00GB内存的PC，操作系统为Windows XP，仿真结果如表2所示。

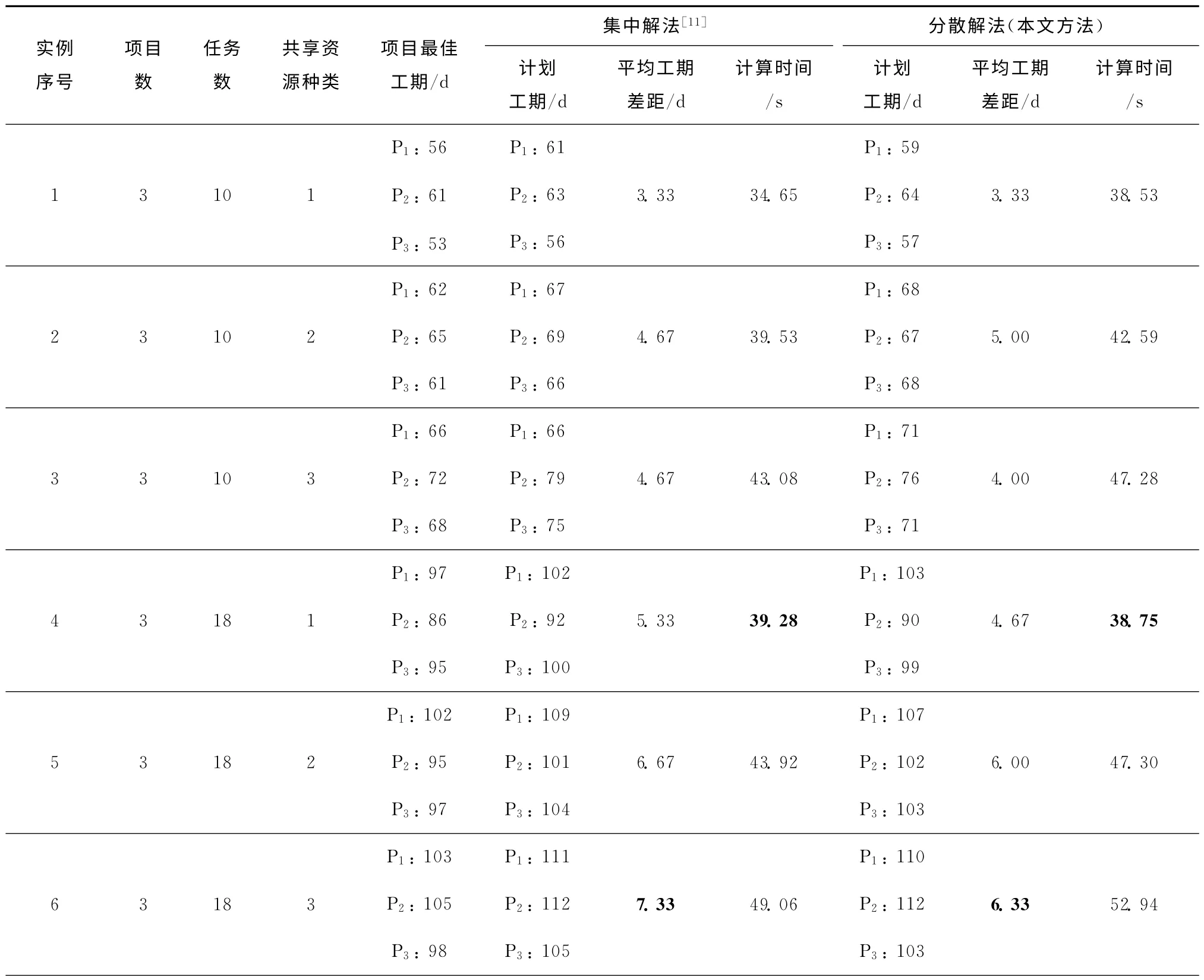
表2 分散式解法与集中式解法的仿真结果比较

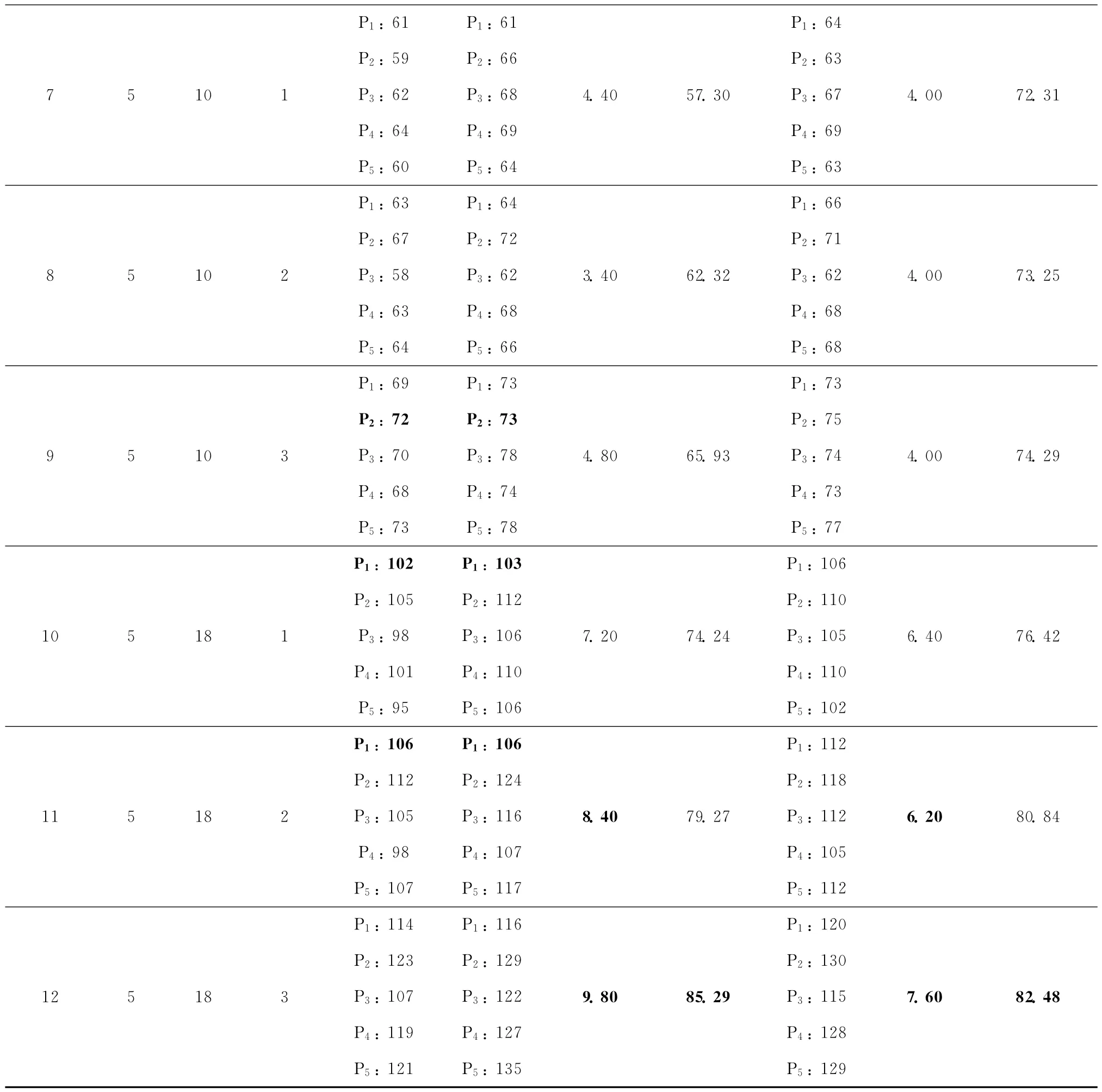
续表2

4.2 仿真结果分析

根据以上仿真计算结果，从单项目最佳工期寻优效果、多项目平均工期差距、弹性任务数规模对结果的影响、基于市场竞争判优的资源分配方式和算法时间性能等方面，对分散解法的求解性能进行比较分析。

（1）单项目最佳工期寻优效果

仿真结果中集中／分散解法的“计划工期”与“最佳工期”的差值反映了不同解法对单一项目最佳工期的寻优效果，即能否使某个（些）项目的工期更加接近理论最优值。从表2中的结果可以发现，集中解法能够针对第3，7和9组实例获得其中一个项目的最佳工期，并对第9和10组实例获得相差仅为1 d的近似最优解，相比而言，分散解法没有获得任何项目的最佳工期。这是因为集中解法在多项目资源冲突判优时采用的是优先级判优方法，在求解过程中对认定为优先级更高的项目分配了更急需的资源，从而可能达到使该项目获得更接近单项目最佳工期的结果；另一方面，由于强制保证了优先级高的项目获得资源，导致优先级偏低的项目难以获得急需资源而不得不推迟工期，在结果中也可以看到，虽然集中解法保证了某些高优先级项目的最佳工期，但是同组的其他项目工期往往都有较大的优化差距。而分散解法虽然难以实现某个项目的最佳工期，但是由于引入了市场竞争判优机制，能够更好地获得大多数项目的近似最优工期。

（2）多项目平均工期差距

在分析了单一项目的最佳工期寻优效果的基础上，进一步分析并行多项目的平均工期差距，此项结果能够反映多项目对理论最优值的平均寻优效果。从表2中的结果可以看出，在工期跨度为［56，135］d范围内的所有项目中，计划工期与最佳工期的差值一般在［3，10］d之间，在此基础上，本文解法（分散解法）对第6，11和12组实例比集中解法缩短1d以上的差距，这对于工期跨度不是很大的项目具有一定的价值。结合上文对“单项目最佳工期寻优效果”的分析，分散解法之所以能够在这些实例上获得更小的多项目平均工期差距，是因为舍弃了对某一个项目最优值的寻优，而通过分散式的局部优化与竞争判优获得多项目整体的寻优效果。

（3）弹性工期任务规模对结果的影响

在以上对多项目平均工期差距进行比较分析的基础上，进一步分析弹性工期任务规模对结果的影响。算例中假定弹性工期任务占项目所有任务的比例在40%，而对于12组测试算例中，本文方法（分散解法）对任务数为18的6组算例计算结果优于任务数为10的6组算例。分析可知，由于分散解法通过多个项目分散式的局部优化决策，更好地利用了“工期弹性”这一特征，能够实现项目工期更加趋近于理论最佳工期，而任务数多的算例由于弹性工期的任务数更多，给分散式局部寻优和协调提供了更大的空间。因此可以认为，分散式解法对于项目规模更大、弹性工期任务数量更多的多项目调度问题具有相对更好的表现。

（4）基于市场竞争判优的资源分配方式

不同于集中式方法事先依据项目优先级判优实现多项目资源分配协调的方式，分散式求解方法采用基于分散式独立决策的思想，事先没有界定各个项目优先级，而是采用基于市场竞争判优的方式实现对多项目资源争用冲突的消解和资源分配。为了进一步检验这种判优方式对多项目资源协调分配的效果，在上述实验的基础上进一步分析第12 组案例。

表2中的第12组案例包含5个项目，这些项目分散式地优化各自的项目计划，对共享资源提出争用请求，依据前文描述的组合拍卖品价格竞标与价格调整方法，对存在争用冲突的资源提高价格，各个项目再次出价，直到“价高者得”最终实现资源的分配与协调，因此竞争成本是项目为了获得共享资源所必须付出的代价，能够付出的竞争成本越高，表明该项目拥有的资源竞争能力更强，应该得到更加接近最佳工期的优化调度结果。第12组案例中的5个项目通过迭代组合拍卖竞争共享资源，最终形成的竞争判优对多项目协调的区分效果，如图4所示。

从结果可以看出，第一次迭代时因为所有共享资源的拍卖价格都取保留价格，所以5个项目的竞争成本都为0；随着迭代次数的增加，某些时间段的共享资源由于争用冲突而进行价格调整，每个项目对共享资源的使用引起项目竞争成本的增加；经过大约30步后，5个项目的竞争成本有了明显的区别并保持稳定。结果表明，5个项目的竞争成本降序排列为项目1＞项目2＞项目5＞项目3＞项目4，将此结果与表2中第12组案例的结果进行比较，可以看出“单项目最佳工期寻优效果”也符合该排序，因此证明通过市场竞争判优的方式实现了对资源的分配协调，达到了越具有竞争能力的项目所获得的调度结果，越接近理论最优的最佳工期。

（5）算法时间性能分析

从算法时间复杂度的角度分别对典型的集中式多项目调度算法以及本文提出的分散式算法进行分析。假设：m表示项目个数，n表示每个项目包含任务数量的上限表示在分散式决策过程中为资源时间槽（拍卖品）设定的保留价格。分散式多项目调度与协调优化方法的计算过程主要包括求解单项目最佳工期的禁忌搜索和基于市场机制的多项目协调两部分。禁忌搜索算法的邻域结构是通过改变当前解中一项弹性任务的工期构造的，假设：项目包括n项任务，单项目工期优化过程的时间复杂度为Ο（n）；同时段并行计划与调度m个项目，在基于市场机制的多项目协调过程中，资源时间槽（拍卖品）价格调整的上限为保留价格，于是分散式多项目调度与协调优化方法的整体时间复杂度为Ο（m×n×。另一方面，集中式解法的求解过程与项目个数以及任务上限有关，在不考虑种群规模等常数因素的情况下算法的时间复杂度为Ο（m×n）。

对照数值仿真实验结果进行分析，从表2中的仿真结果可以看出，12组测试算例中有10 组结果在计算时间方面的集中式方法短于分散式方法，进一步证明了在时间性能方面分散式解法存在差距，但是能够满足对求解速度要求不是非常严格的多项目调度场景的实际应用需要。

基于以上仿真实验和分析，得出集中解法与分散解法的定性比较结果，如表3所示。

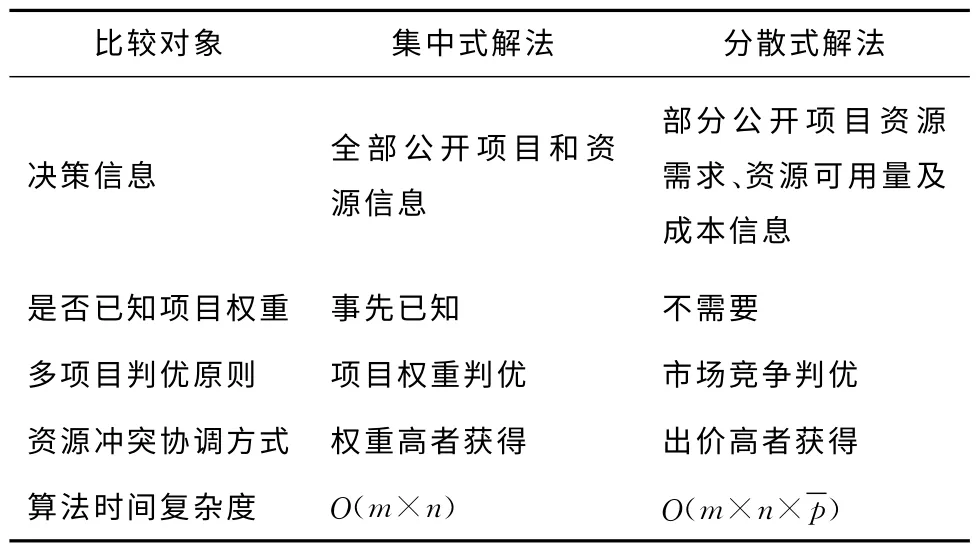
表3 集中式解法与分散式解法的定性比较

由比较分析可见，首先，对于能够获得项目和资源所有信息的多项目调度问题，可以采用集中式解法，而对于跨组织协同等环境下由于私有信息保留难以获得所有信息的问题，需要采用分散式解法，在多个决策主体局部优化的前提下，各自公开部分信息进行协同决策；其次，对于事先已知项目权重的多项目调度问题可以采用集中式解法，在资源冲突时通过项目权重判优协调资源分配，而如果事先难以获知项目权重或者项目权重信息不可靠、变化等情况，则采用不需要权重的分散式解法相对更好，可以通过市场竞争判优的方式，借助拍卖方式协调多项目对共享资源的争用。

综上所述，通过仿真实验与结果的讨论分析，从单项目最佳工期寻优效果、多项目平均工期差距、弹性工期任务规模对结果的影响、基于市场竞争判优的资源分配方式以及算法时间性能等不同角度，对本文提出的考虑工期弹性的分散式项目调度协调优化方法进行了递进式分析，验证了分散式方法在获得多项目平均优化效果、未知优先级的情况下，对多项目资源竞争分配的判优方面有优于集中方法的性能，而在事先已知项目优先级情况下的偏重项目最佳工期优化效果劣于集中式方法。两者间的优势与不足可以在实际求解和工程应用中取长补短，针对不同的问题和求解重点进行选择。

5 结束语

本文提出融合多项目、以项目成本最小为目标的局部优化与共享资源竞标出价、资源组合拍卖与价格迭代调整的分散式多项目调度协调优化方法，通过分散式优化与市场竞争判优协调方式解决了集中式方法难以求解的项目优先级未知环境下的平均项目工期优化问题；针对其中的单项目工期优化过程，采用嵌入工期弹性调整的禁忌搜索算法，该方法根据分散式多项目调度问题的特点，实现了在满足工期底限的约束下寻找项目成本最小的最佳工期，更具有实用价值。实验表明：所提出的分散式项目调度协调优化方法能够获得比集中式解法更短的平均项目工期优化差距，且验证了通过分散式优化与竞争判优能够较好地解决难以事先预判优先级的多项目调度问题。

［1］CONFESSORE G，GIORDANI S，RISMONDO S.A marketbased multi-agent system model for decentralized multi-project scheduling［J］.Annals of Operations Research，2007，150（1）：115-135.

［2］HOMBERGER J.A（μ，λ）-coordination mechanism for agentbased multi-project scheduling［J］.OR Spectrum，2009，34（1）：107-132.

［3］LAU J S K，HUANG G Q，MAK K L，et al.Distributed project scheduling with information sharing in supply chains：part I-an agent-based negotiation model［J］.International Journal of Production Research，2005，43（22）：4813-4838.

［4］LEE Y，KUMARA S R T，CHATTERJEE K.Multiagent based dynamic resource scheduling for distributed multiple projects using a market mechanism［J］.Journal of Intelligent Manufacturing，2003，14（5）：471-484.

［5］YING Ying，SHOU Yongyi.Resource-constrained multi-project scheduling based on combinatorial auction method［J］.Computer Integrated Manufacturing Systems，2009，15（11）：2160-2165（in Chinese）.［应 瑛，寿涌毅.基于组合拍卖方法的资源受限多项目调度［J］.计算机集成制造系统，2009，15（11）：2160-2165.］

［6］ARAUZO J A，GALAN J M，PAJARES J，et al.Multi-agent technology for scheduling and control projects in multi-project environments.an auction based approach［J］.Inteligencia Artificial，2009，13（42）：12-20.

［7］WANG Lei，ZHAN Dechen，NIE Lanshun，et al.Optimization method for block erection scheduling with activity duration elasticity［J］.Computer Integrated Manufacturing Systems，2011，17（7）：1478-1485（in Chinese）.［王 磊，战德臣，聂兰顺，等.考虑任务工期弹性的船台吊装计划优化方法［J］.计算机集成制造系统，2011，17（7）：1478-1485.］

［8］BAI Jiancong，CHANG Huiyou，YI Yang.Modeling and heuristic for winner determination in combinatorial auctions［J］.Journal of Computer Research and Development，2005，42（11）：1856-1861（in Chinese）.［白鉴聪，常会有，衣 杨.获胜者确定问题的建模与启发式算法［J］.计算机研究与发展，2005，42（11）：1856-1861.］

［9］JIN Xing，SHI Chunyi.A winner determine algorithm for combinatorial auctions with decreasing［J］.Journal of Computer Research and Development，2006，43（7）：1142-1148（in Chinese）.［金 涬，石纯一.一种边际效用递减组合拍卖的胜者决定算法［J］.计算机研究与发展，2006，43（7）：1142-1148.］

［10］KOLISCH R，HARTMANN S.Experimental investigation of heuristics for resource-constrained project scheduling：an update［J］.European Journal of Operational Research，2006，174（1）：23-37.

［11］PETEGHEM V V，VANHOUCKE M.A genetic algorithm for the preemptive and non-preemptive multi-mode resourceconstrained project scheduling problem［J］.European Journal of Operational Research，2010，201（2）：409-418.