作业车间调度的空闲时间邻域搜索遗传算法

赵诗奎，方水良，顾新建

（浙江大学 机械工程学系工业工程中心，浙江 杭州 310027）

0 引言

作业车间调度问题（Job shop Scheduling Problem，JSP）是典型的组合优化问题之一，自20 世纪50年代以来，一直是学术界研究的热点和难点。先进的车间调度方法对提高车间生产效率和降低能耗具有重要的实际应用价值。JSP的求解方法主要分为精确法和近似法，精确法的时间复杂度较高，随着问题规模的增大，将变得不可行；近似法虽然不能保证求得最优解，但通常能够在可行的时间内求得近优解，在合理计算时间内提高近似法解的质量，是所要研究的重要问题。

目前，近似方法中以遗传算法、禁忌算法、粒子群算法、模拟退火算法和文化算法等为代表的智能算法在求解JSP 中得到了成功应用。为提高智能算法求解JSP的能力，国内外学者开展了一系列研究。文献［1］将人工免疫系统与禁忌算法混合求解JSP，提出AIS-TS算法；文献［2］在文化算法中融入局部搜索，对求解JSP进行了研究；文献［3］将瓶颈移动与动态自适应邻域搜索过程混合对JSP 进行求解，提出F&F 算法；文献［4］将粒子群算法与人工免疫系统混合求解JSP，提出PSO-AIS算法；文献［5］将局部搜索与遗传算法混合求解JSP；文献［6］采用块结构的交换邻域和插入邻域，嵌入离散差分进化算法中求解JSP；文献［7］将邻域结构引入细菌觅食优化算法趋化操作中，提出求解作业车间调度的变邻域细菌觅食优化算法；文献［8］提出一种基于动态调整能力全局邻域交换策略的调度算法；文献［9-10］采用基于邻域结构的禁忌算法求解JSP，取得了显著成效。已有研究表明，针对单一算法局部搜索或全局搜索能力差的问题，将不同算法进行混合，可以实现不同算法全局和局部搜索能力的优势互补，是改善算法搜索能力的重要途径；此外，研究JSP本身的特征领域知识，将其融入智能算法的求解过程，对于指导算法的搜索方向，进而提高搜索效率和改善求解结果，具有重要的意义。

本文将基于空闲时间的邻域搜索融入到遗传算法求解JSP。邻域结构的设计是JSP特征领域知识的重要体现，本文通过对不同解码方式进行分析，基于利用机器空闲时间减小最大完工时间的想法，设计了一种基于空闲时间的邻域结构，典型算例的测试结果验证了所提方法的有效性。

1 问题模型

JSP可以描述为n个工件｛Ji｜（i=1，2，…，n）｝在m台机器｛Mj｜（j=1，2，…，m）｝上加工，工件加工过程需满足的约束条件包括：Ji在同一时刻只能在一台机器上加工；Ji的工序加工过程需满足Ji工艺路线的要求；Mj在同一时刻只能加工一个工件；工序在机器上一旦开始加工就不能中断，直至完成。表1所示为一个3×3的JSP实例。本文以最大完工时间Cmax（或makespan）最小为目标函数，以Ci为工件Ji的完工时间，目标函数为

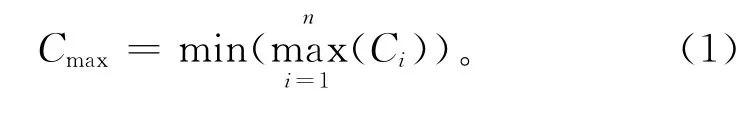
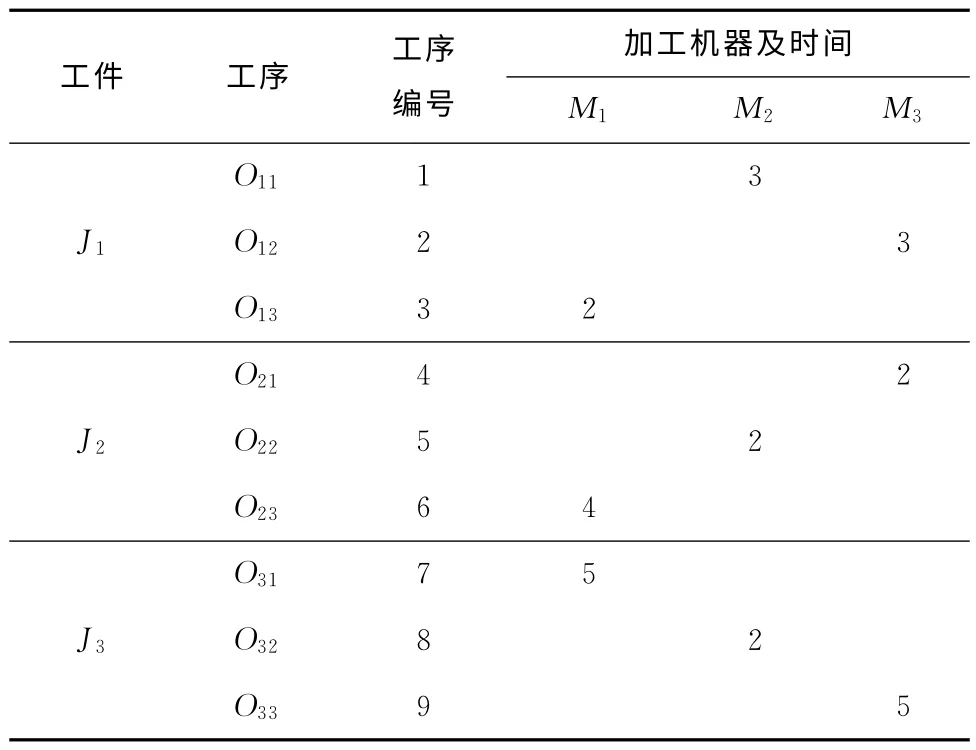
表1 3×3JSP实例

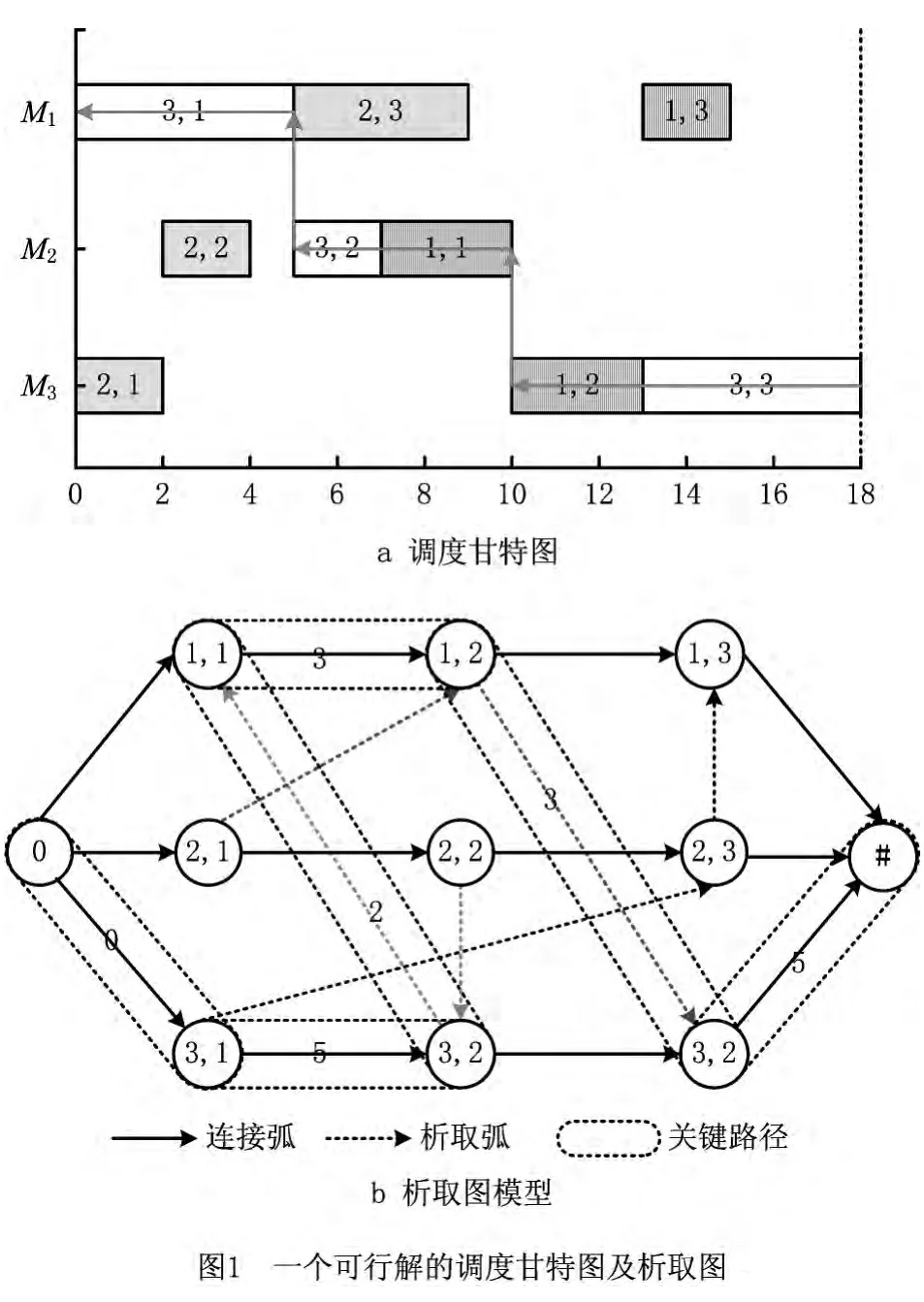
析取图模型是描述JSP 和对其进行理论分析的有力工具，JSP 的析取图模型［11］定义为G=（N，A，E）。其中：N为所有工件的工序节点以及2个虚节点（开始节点和结束节点，分别用0和＃表示）组成的集合；A为同一工件相邻两道工序间的连接弧集合，对应于工件的工艺路线约束；E为同一机器两道工序间的析取弧集合。确定所有机器上工序的加工顺序后，得到最终的析取图G′，当G′中不包含有向回路时对应一个可行解。L（u，v）表示G′中从工序u的节点到工序v的节点最长路径的长度，调度的最大完工时间makespan=L（0，＃）。图1a所示为表1实例的一个可行解所对应的调度甘特图，图1b为其对应的析取图模型。调度甘特图中，工序间无时间间隔的最长路径称为关键路径，在对应的析取图模型中，关键路径为从开始节点0到结束节点＃的最长路径，组成关键路径的工序定义为关键工序。采用文献［12］中的关键路径查找方法，得到的关键路径如图1a箭头和图1b虚线框所示，在关键路径上的工序为关键工序，否则为非关键工序。

2 基于空闲时间的邻域结构

2.1 解码方式分析

目前，针对JSP，一般都要先确定一个工序顺序码，通过解码得到一个调度及其甘特图。其解码方式主要有半主动、主动和全主动方式［13］。对于某JSP问题的工序顺序码［2 2 1 1］，图2a所示为半主动解码得到的调度甘特图，工序的开工时间等于其工件前道工序和机器前道工序完工时间的最大值。主动解码是在半主动解码的基础上，通过对工序左移的方式获得，解码时查找工序前面的可用机器空闲时间，在不推迟其他已安排工序开工时间的条件下，将其插入对应机器上最早可行的加工时刻。图2b所示为对图2a中工序O1，1左移后的调度结果，最大完工时间由8 减小到5。在主动解码的基础上，全主动解码增加了对工序的右移操作，通过查找工序后面的可用机器空闲时间来实现。如图3a所示，对于编码［1 1 2 2］，主动解码所得到的调度结果，在不推迟其他工序开工时间的条件下，每道工序后面依然有可能存在可用空闲时间段。将图3a中的工序O1，2左移后得到图3b，最大完工时间由8减小到5。

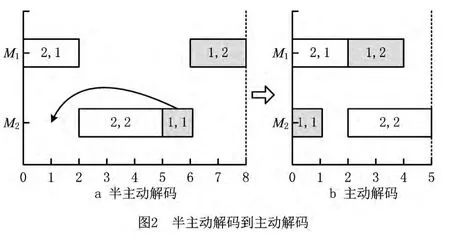
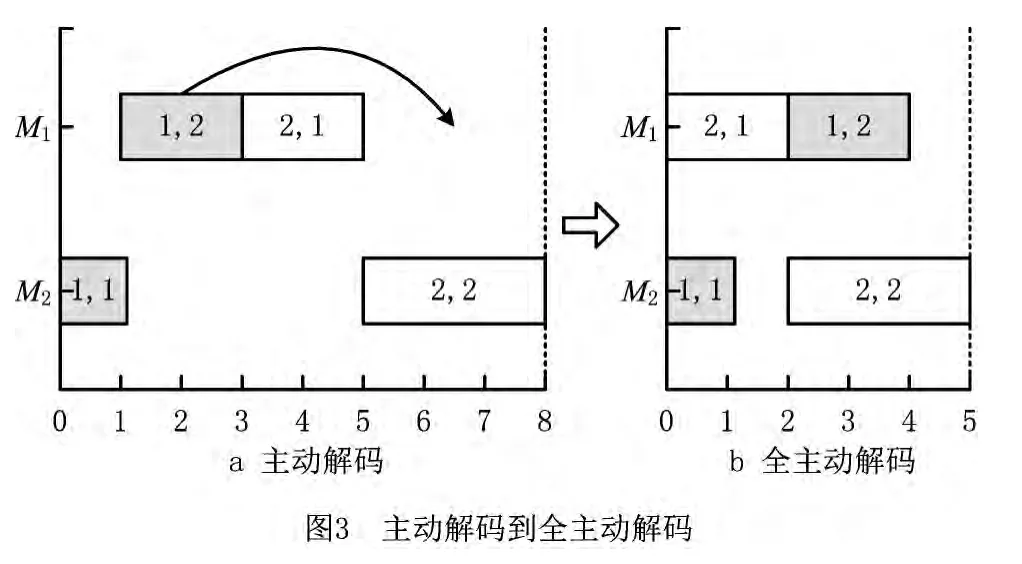
可见，主动解码和全主动解码的基本思想都是通过查找工序的可用空闲时间，进而利用该空闲时间来减小调度目标的最大完工时间。主动解码在半主动解码的基础上，通过左移工序实现；全主动解码在主动解码的基础上，通过右移工序实现。主动解码和全主动解码都是在不延迟其他任何工序开工时间的情况下移动工序，即当空闲时间段足以加工该工序时才对工序进行移动，当空闲时间段不足以加工该工序时，不对工序进行移动。两种解码方式仅利用机器空闲时间段中足够大的可用空闲时间段，没有考虑不足以使用的小的空闲时间段。

然而，通过延迟其他工序，利用不足以加工工序的小的空闲时间段，依然可能减小最大完工时间。图4所示为表1实例的一种调度，对工序O1，1的空闲时间进行分析，图4a为一个主动解码调度甘特图，在不延迟其他工序开工时间的条件下，每道工序前面不存在足以加工该工序的空闲时间段。图4a的工序O1，1前面存在2个空闲时间段，在图中分别标记为①②，它们都不足以加工O1，1。但将O1，1移动到2 个空闲时间段位置后，分别得到图4b 和图4c，最大完工时间由18 分别减小到12 和15，可见通过利用不足以加工工序O1，1的小的空闲时间段，虽然延迟了部分其他工序，但是仍然能够减小最大完工时间。

基于利用机器空闲时间减小最大完工时间的想法，本文构造了一种基于空闲时间的邻域结构。因为最大完工时间取决于关键路径的长度，所以对关键工序查找机器空闲时间进行邻域移动搜索。对关键工序进行邻域移动时面临的问题是：什么条件下移动关键工序不会产生不可行解，以及如何最大限度地查找属于该工序的机器空闲时间。只有解决了这两个问题，才能在保证可行解的条件下扩大关键工序的邻域搜索范围，提高JSP问题的求解能力。

2.2 保证可行解工序的移动条件

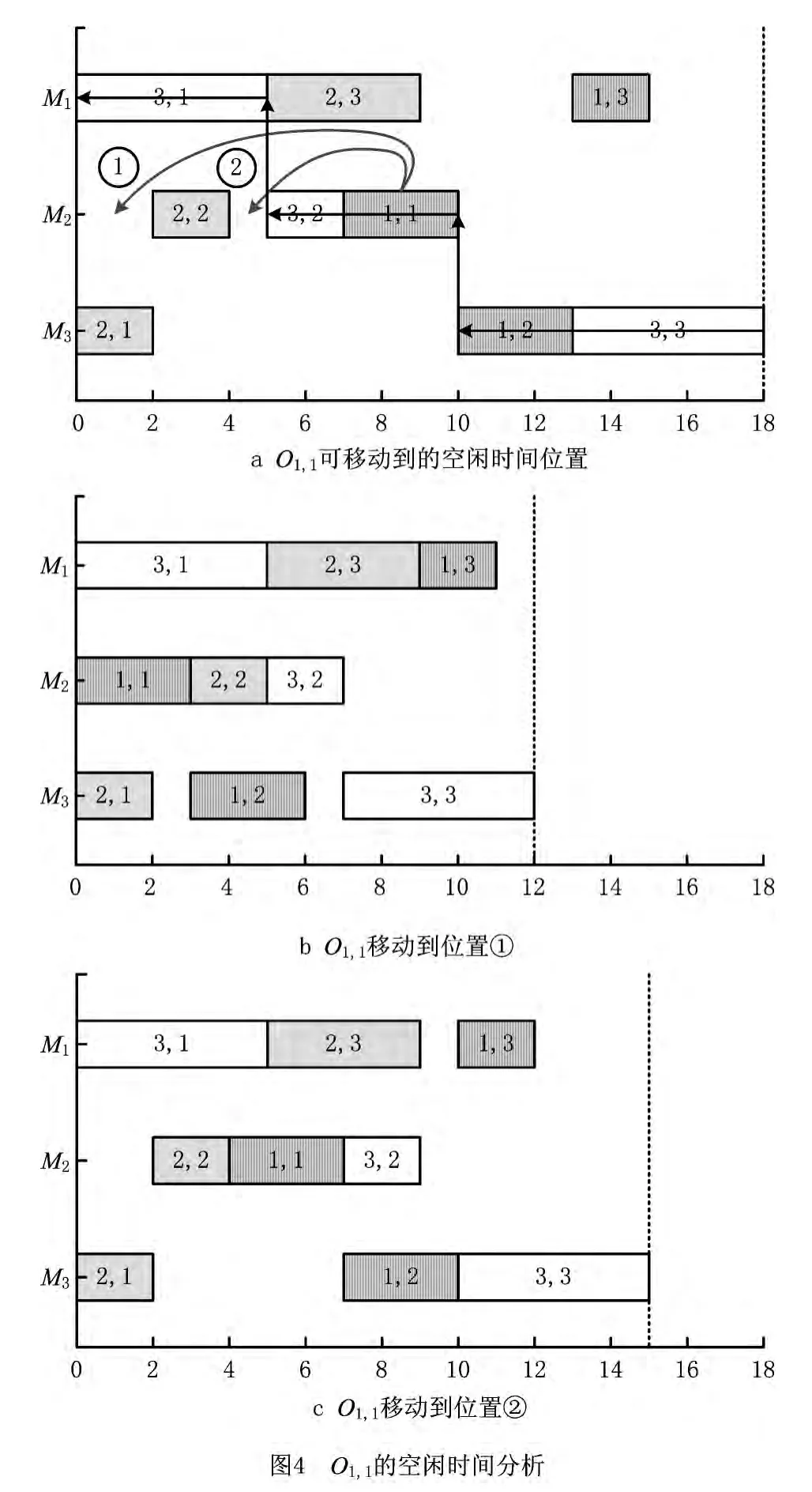
文献［9，14］分别提出针对两个关键工序进行位置相对移动时，保证可行解的关键工序移动条件，其中文献［9］对文献［14］定理的适用范围进行了扩展，将适用范围扩展到了同一台机器上的任意两个关键工序。由于基于空闲时间进行工序的邻域移动时，必然涉及到关键工序与非关键工序位置间的相对移动。如图4a中的工序O1，1和O2，2，O1，1是关键路径上的关键工序，O2，2不是关键工序，因此必须考虑关键工序与非关键工序位置间相对移动时保证可行解的工序移动条件。为此，本文对文献［9］中定理的适用范围进行了进一步扩展并给出了证明，使其能够适用于同一台机器上的任意两个工序，取消了关键工序条件限制。

为了对定理进行证明，首先对以下符号进行说明：G′为可行解s对应的析取图模型，s的最大完工时间为makespan，工序u的机器前道工序和后续工序分别为MP［u］，MS［u］，工件前道工序和后续工序分别为JP［u］，JS［u］；工序u的加工时间为pu，最早开工时间和最早完工时间分别为sE（u）和cE（u），则cE（u）=sE（u）+pu，最晚开工时间和最晚完工时间分别为sL（u）和cL（u），则cL（u）=sL（u）+pu。

定理1 对于一个可行解s，同一台机器上的任意两个工序为u和v，假设u在v前加工，如果满足下列条件之一，则移动工序u至工序v之后仍然是可行解：①工序u为工件的末道工序，JS［u］不存在；②JS［u］存在且L（v，＃）≥L（JS［u］，＃）。

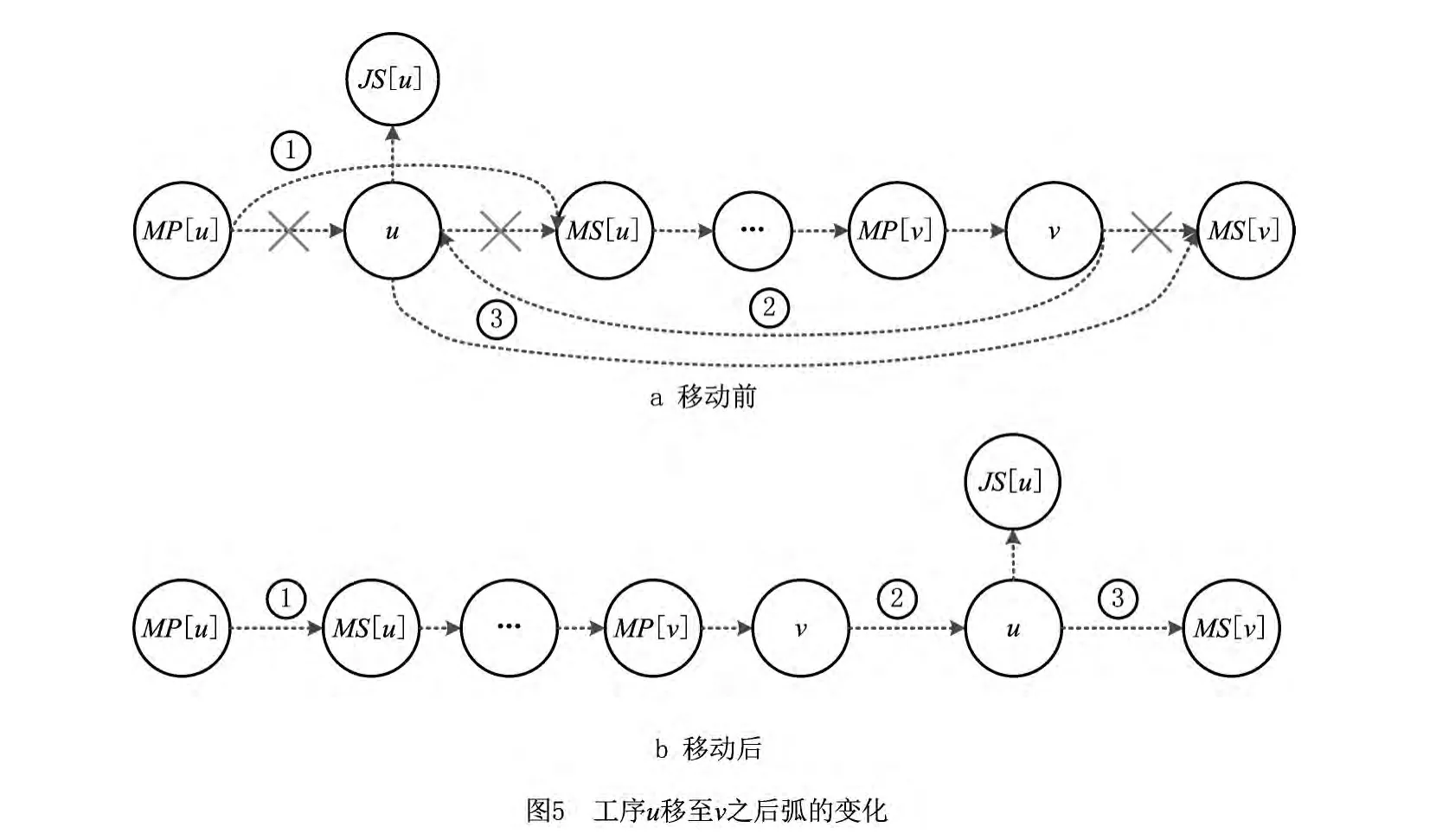
证明 图5a所示为工序u移至工序v之后弧的变化，弧①②③为新增的3条弧，对图5a工序的位置顺序进行整理，得到图5b；工序u移至工序v之后，如果产生有向回路，则有向回路必包含新增的弧［15］，采用反证法证明新增的3条弧都不可能出现在有向回路中。

如果新增弧①（MP［u］→MS［u］）出现在有向回路中，则G′中必存在有向路径（MS［u］→MP［u］），与s是可行解矛盾，因此新增弧①不可能出现在有向回路中。

如果新增弧②（v→u）出现在有向回路中，则G′中必存在有向路径（u→v），根据有向路径（u→v）在图5b节点u处的分支，可以分为两类：①有向路径（u→MS［v］→v）；②有向路径（u→JS［u］→v）。

如果第①类有向路径（u→MS［v］→v）存在，则G′中必存在有向路径（MS［v］→v），与s是可行解矛盾，因此第①类有向路径（u→MS［v］→v）不存在。对于第②类有向路径（u→JS［u］→v），当JS［u］不存在时，显然有向路径（u→JS［u］→v）不存在；当JS［u］存在时，如果有向路径（u→JS［u］→v）存在，则必有L（v，＃）＜L（JS［u］，＃），与条件L（v，＃）≥L（JS［u］，＃）矛盾，因此当JS［u］存在且L（v，＃）≥L（JS［u］，＃）时，第②类有向路径（u→JS［u］→v）不存在。所以有向路径（u→v）不存在，新增弧②（v→u）不可能出现在有向回路中。

如果新增弧③（u→MS［v］）出现在有向回路中，则G′中必存在有向路径（MS［v］→u），与s是可行解矛盾，因此新增弧③不可能出现在有向回路中。证毕。

定理2 对于一个可行解s，同一台机器上任意两个工序为u和v，假设u在v前加工，如果满足下列条件之一，则移动工序v至u之前仍然是可行解：①工序v为工件的首道工序，JP［v］不存在；②JP［v］存在且L（0，u）+pu≥L（0，JP［v］）+pJP［v］。

证明 图6a所示为工序v移至工序u之前弧的变化，弧①②③为新增的3条弧，对图6a工序的位置顺序进行整理，得到图6b；工序v移至工序u之前，如果产生有向回路，则有向回路必包含新增的弧，采用反证法证明新增的3条弧都不可能出现在有向回路中。

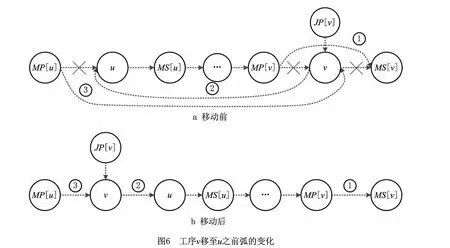
如果新增弧①（MP［v］→MS［v］）出现在有向回路中，则G′中必存在有向路径（MS［v］→MP［v］），与s是可行解矛盾，因此新增弧①不可能出现在有向回路中。

如果新增弧②（v→u）出现在有向回路中，则G′中必有有向路径（u→v）存在。在图6b 中，按照节点v之前紧邻节点的不同，有向路径（u→v）可以分为2类：①有向路径（u→MP［u］→v）；②有向路径（u→JP［v］→v）。

如果第①类有向路径（u→MP［u］→v）存在，则G′中必存在有向路径（u→MP［u］），与s是可行解矛盾，因此第①类有向路径（u→MP［u］→v）不存在。对于第②类有向路径（u→JP［v］→v），当JP［v］不存在时，显然有向路径（u→JP［v］→v）不存在；当JP［v］存在时，如果有向路径（u→JP［v］→v）存在，则必有L（0，u）+pu＜L（0，JP［v］）+pJP［v］，与条件L（0，u）+pu≥L（0，JP［v］）+pJP［v］矛盾，因此当JP［v］存在且L（0，u）+pu≥L（0，JP［v］）+pJP［v］时，第②类有向路径（u→JP［v］→v）不存在。所以有向路径（u→v）不存在，新增弧②（v→u）不可能出现在有向回路中。

如果新增弧③（MP［u］→v）出现在有向回路中，则G′中必存在有向路径（v→MP［u］），与s是可行解矛盾，因此新增弧③不可能出现在有向回路中。证毕。

换一个角度，利用工序的最早开完工时间和最晚开完工时间分析两个定理。对于定理1，当JS［u］不存在时，工序u可以移至同台机器工序u之后的任意工序v后面；当JS［u］存在时，因为

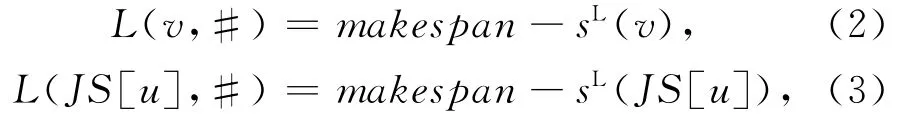
所以条件L（v，＃）≥L（JS［u］，＃）等价于sL（v）≤sL（JS［u］），即：

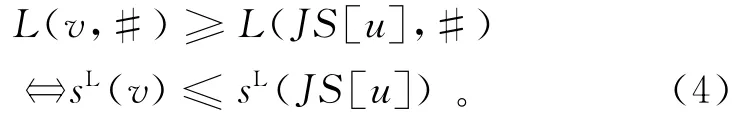
对于定理2，当JP［v］不存在时，工序v可以移至同台机器工序v之前的任意工序u前面；当JP［v］存在时，因为

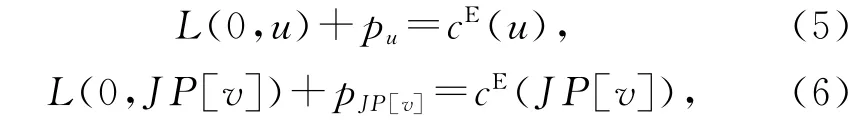
所以条件L（0，u）+pu≥L（0，JP［v］）+pJP［v］等价于cE（u）≥cE（JP［v］），即

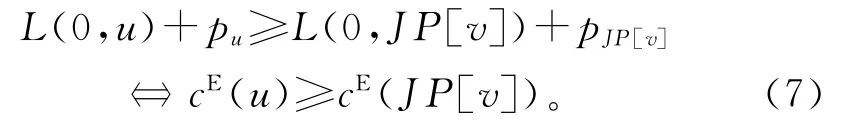
2.3 空闲时间查找与邻域结构

同一台机器上，相邻两道工序为x，y，假设x先于y加工，工序x，y之间的最大空闲时间（idle time）定义为IT（x，y）。当工序x的完工时间最早、工序y的开工时间最晚时，空闲时间IT（x，y）达到最大值［16］，即IT（x，y）=sL（y）-cE（x）。在如图7a所示的调度甘特图中，在不改变机器上工序加工顺序的前提下，图中对应的是每道工序的最早开工时间和最早完工时间，图中工序w满足sE（w）=max｛cE（JP［w］），cE（MP［w］）｝。在最大完工时间和每台机器上工序加工顺序不变的条件下，将图7a中的工序移至其最晚完工时间，得到图7b，此时甘特图中对应的是每道工序的最晚开工时间和最晚完工时间，满足cL（w）=min｛sL（JS［w］），sL（MS［w］）｝。如果JP［w］或MP［w］不存在，则用虚拟开始节点工序0代替，cE（0）=0；如果JS［w］或MS［w］不存在，则用虚拟结束节点工序＃代替，sL（＃）=makespan。

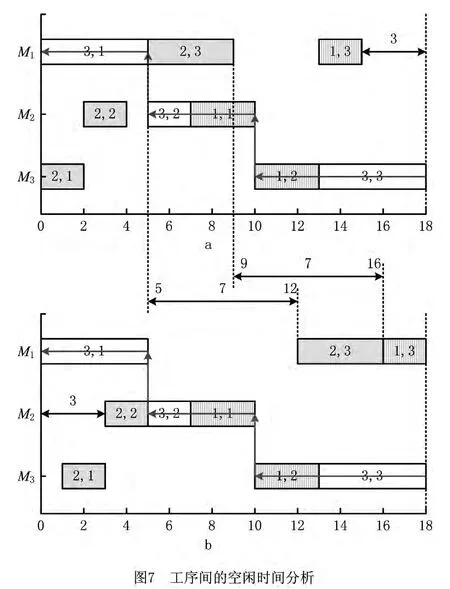
结合图7解释两道工序间的空闲时间，如机器M1上的相邻 两工序O3，1，O2，3，IT（O3，1，O2，3）=sL（O2，3）-cE（O3，1）=12-5=7；当工序为机器的首道工序时，如机器M2上的工序O2，2，该工序前面的最大空闲时间为IT（0，O2，2）=sL（O2，2）-cE（0）=3-0=3；当工序为机器的最后一道工序时，如机器M1上的工序O1，3，该工序后面的最大空闲时间为IT（O1，3，＃）=sL（＃）-cE（O1，3）=18-15=3。

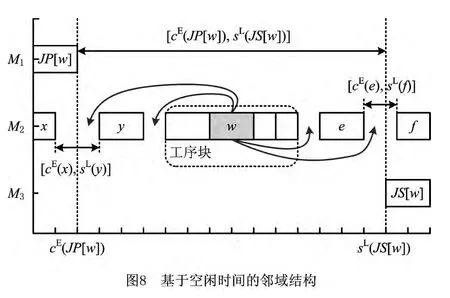
基于空闲时间的邻域结构如图8所示，工序w为工序块上的一个关键工序，属于工序w的机器空闲时间为：从JP［w］的最早完工时间到JS［w］的最晚开工时间，时间段区间［cE（JP［w］），sL（JS［w］）］内，工序w加工机器的空闲时间，当JP［w］不存在时，cE（JP［w］）用0代替，当JS［w］不存在 时，sL（JS［w］）用makespan代替。在时间段区间［cE（JP［w］），sL（JS［w］）］内能够最大限度地查找出工序w的机器空闲时间，但是有可能存在导致死锁的不可用空闲时间。

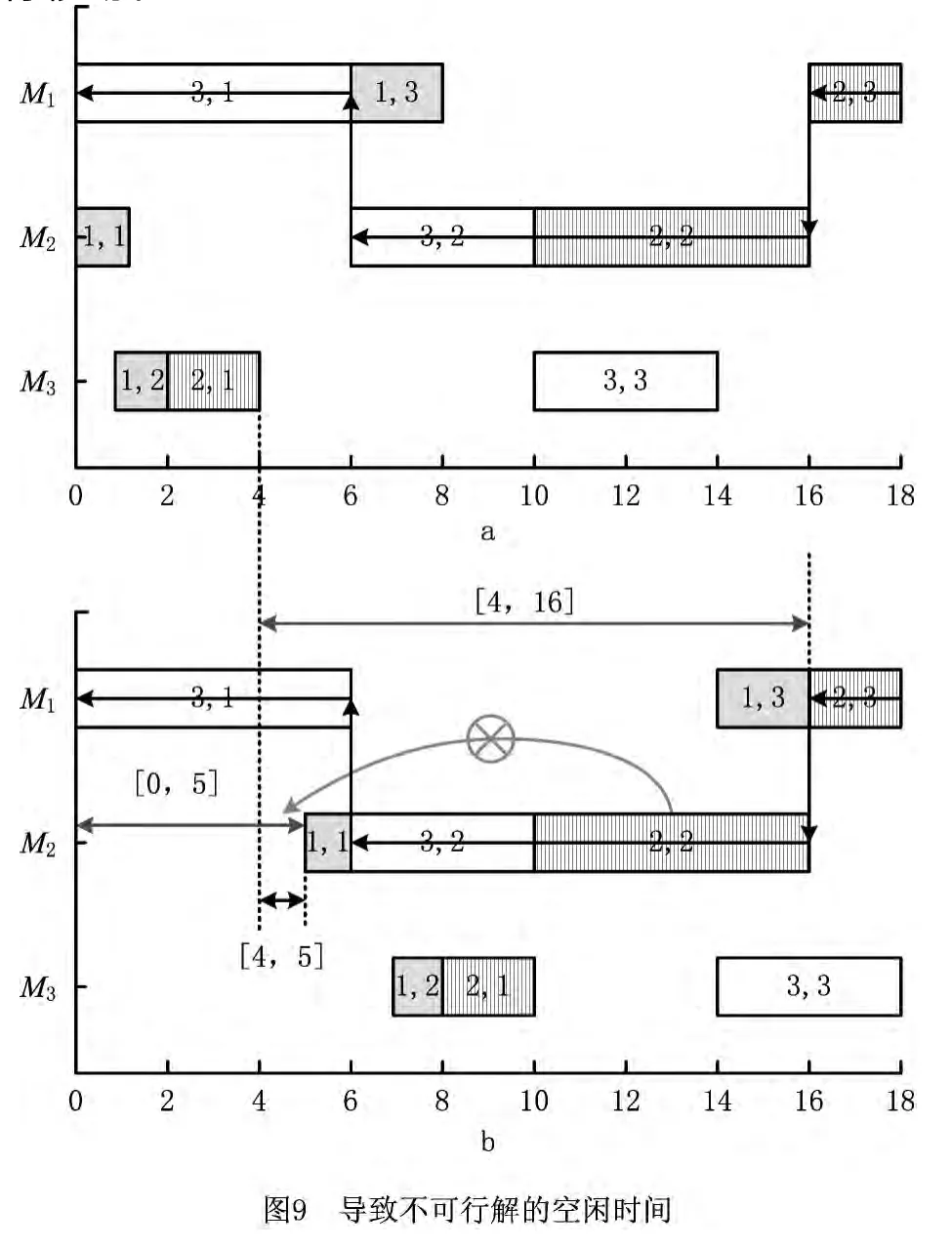
为说明导致不可行解的空闲时间，调整表1中的JSP实例工序的加工时间（J1：1→1→2，J2：2→6→2，J3：6→4→4），加工机器不变，得到新的实例。图9a为新实例的一个调度甘特图，对应每道工序的最早开完工时间，图9b对应每道工序的最晚开完工时间，对于关键工序O2，2，在时间段区间［4，16］内，查找机器M2的可用空闲时间，工序O1，1前面存在可用空闲时间［0，5］∩［4，16］=［4，5］，但是如果将工序O2，2移至O1，1的前面，则在M2，M3的4道工序之间会发生死锁，M2：O2，2→O1，1，M3：O1，2→O2，1，从而导致不可行解。因此，对于查找到的空闲时间，必须在满足保证可行解工序移动条件下才能对工序进行移动。

对工序块的关键工序的邻域移动操作分别如下：

（1）当工序w为块内工序时，对块内工序的邻域移动操作包括前移和后移，因为同一工序块各工序间是紧密连接的，不存在空闲时间，所以块内工序移动时，分别从块首工序开始向前查找和从块尾工序开始向后查找空闲时间。

如图8所示，前移时x和y是两个相邻工序，工序w能否移动到工序y之前需要判断是否满足保证可行解的工序移动条件。在满足移动条件的前提下，当工序y之前的空闲时间段与属于工序w的机器空闲时间区间的交集不为0时，即

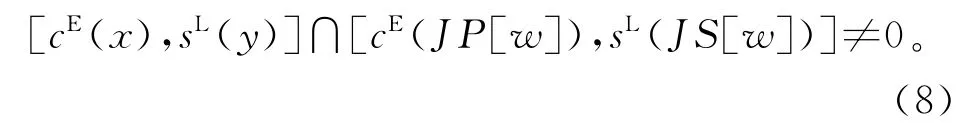
式（8）表示y之前存在工序w的可用空闲时间，将w移动至y前，当sL（y）≤cE（JP［w］）时，［cE（x），sL（y）］∩［cE（JP［w］），sL（JS［w］）］=0，结束向前查找。

后移时e和f是两个相邻工序，工序w能否移动到工序e之后需要判断是否满足工序的后移条件。在满足移动条件的前提下，当工序e之后的空闲时间段与属于工序w的机器空闲时间区间交集不为0时，即

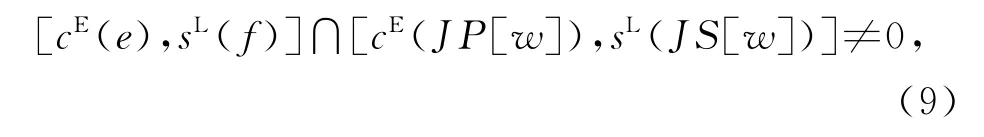
式（9）表示e之后存在工序w的可用空闲时间，w移动至e后，当cE（e）≥sL（JS［w］）时，［cE（e），sL（f）］∩［cE（JP［w］），sL（JS［w］）］=0，结束向后查找。

（2）当工序w为块首工序时，因为块首之前任意两个相邻工序x和y之间的空闲时间满足［cE（x），sL（y）］∩［cE（JP［w］），sL（JS［w］）］=0，不存在可用空闲时间，所以只存在后移操作，从块尾工序开始向后查找空闲时间。当工序w为块尾工序时，因为块尾之后任意两个相邻工序e，f之间的空闲时间满足［cE（e），sL（f）］∩［cE（JP［w］），sL（JS［w］）］=0，不存在可用空闲时间，所以只存在前移操作，从块首工序开始向前查找空闲时间。工序w能否移动的判断条件与块内工序相同。

3 基于邻域搜索的JSP遗传算法及其实验分析

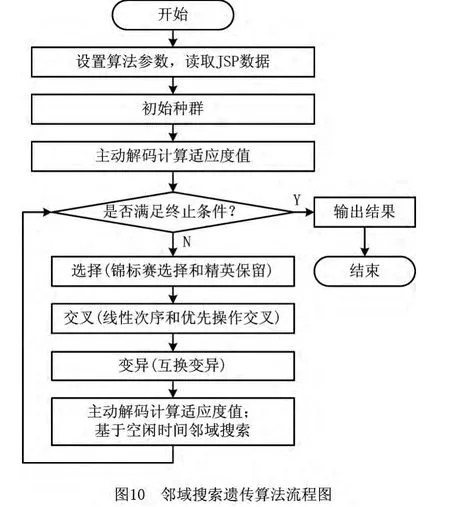
基于空闲时间邻域搜索的JSP 求解遗传算法流程如图10所示。图中采用基于工序的编码方式进行编码，对染色体主动解码计算最大完工时间；遗传操作中，选择方式为锦标赛选择和精英保留策略，交叉方式为线性次序交叉和优先操作交叉，变异方式为互换变异。对新一代群体的每个个体解码之后，再利用本文所提的基于空闲时间的邻域搜索策略进行邻域搜索。

为了验证本文算法的实际效果，在CPU 主频为2.60GHz、内存为2.0GB的计算机上，用Visual Basic编程，对典型算例进行测试。43 个典型算例包括LA01～LA40 算例 和FT06，FT10，FT20 算例，算法参数设置为：每个算例种群规模PopSize如表2所示，交叉概率为0.8，变异概率为0.1，最大代数为100代。每个算例求解20次，每次求解过程中，当最优值连续10代不更新时，结束运行。

将本文算法与目前相关文献中算法的求解结果进行对比分析，5种算法包括文献［1］（2012）的AISTS混合算法、文献［2］（2011）的文化算法、文献［3］（2009）的F&F 算法、文献［4］（2008）的PSO-AIS混合算法和文献［5］（2012）的混合遗传算法。表2所示为43个典型算例求解结果的对比分析，Re为不同算法求解结果的最优值Cmax与典型算例理论最优 值C＊的相对偏差，Re=（Cmax-C＊）／C＊×100%，为了比较不同算法的整体性能，对43个算例的相对偏差求均值Av（Re），根据Av（Re）的大小评价算法。本文算法的Av（Re）=0.21，其余5种算法的Av（Re）分别为0.29，0.33，0.28，0.33，0.18。可见，本文算法整体性能优于其中的4种算法，略差于与文献［5］（2012）的混合遗传算法（Av（Re）=0.18）。

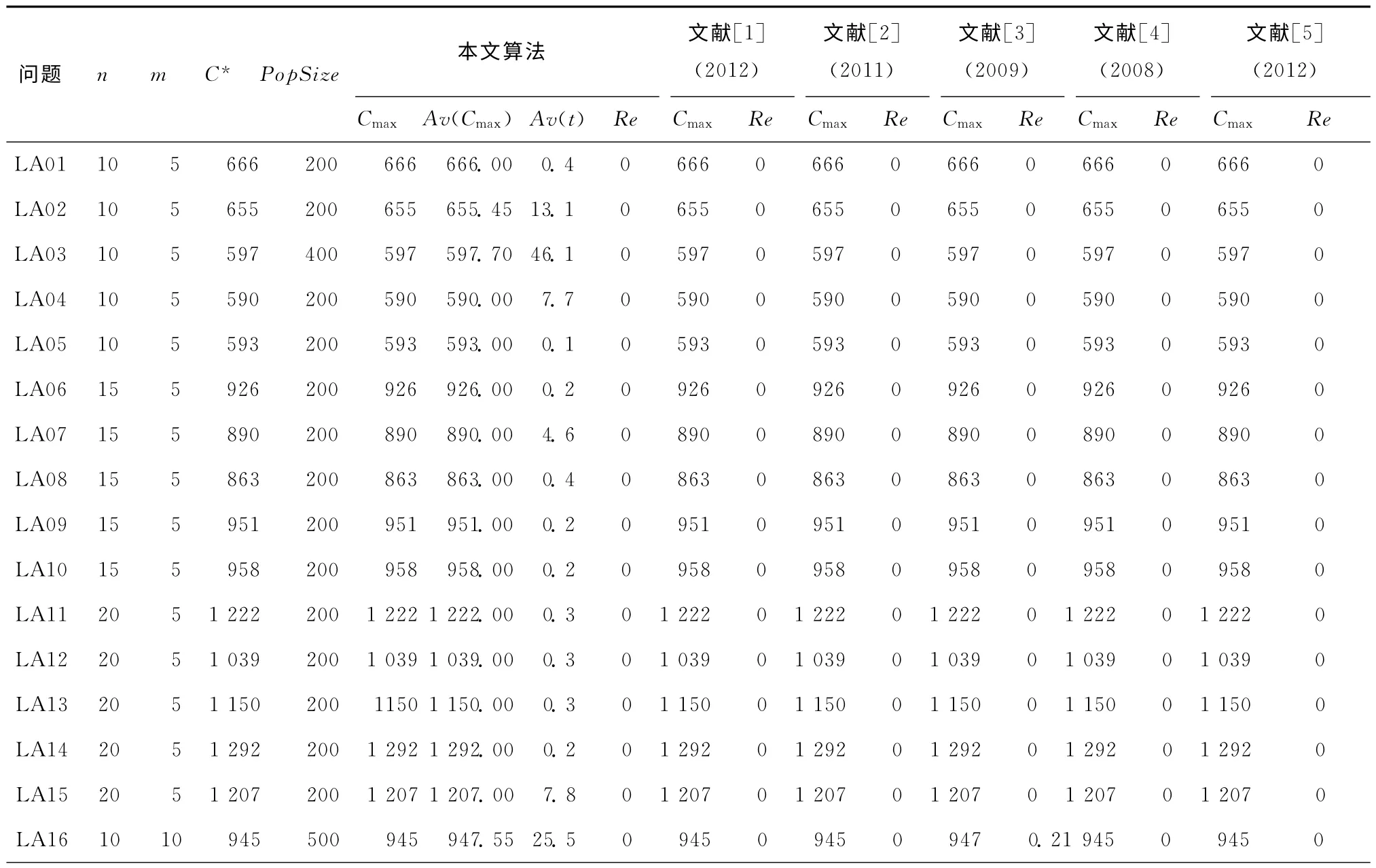
表2 典型算例求解结果对比分析

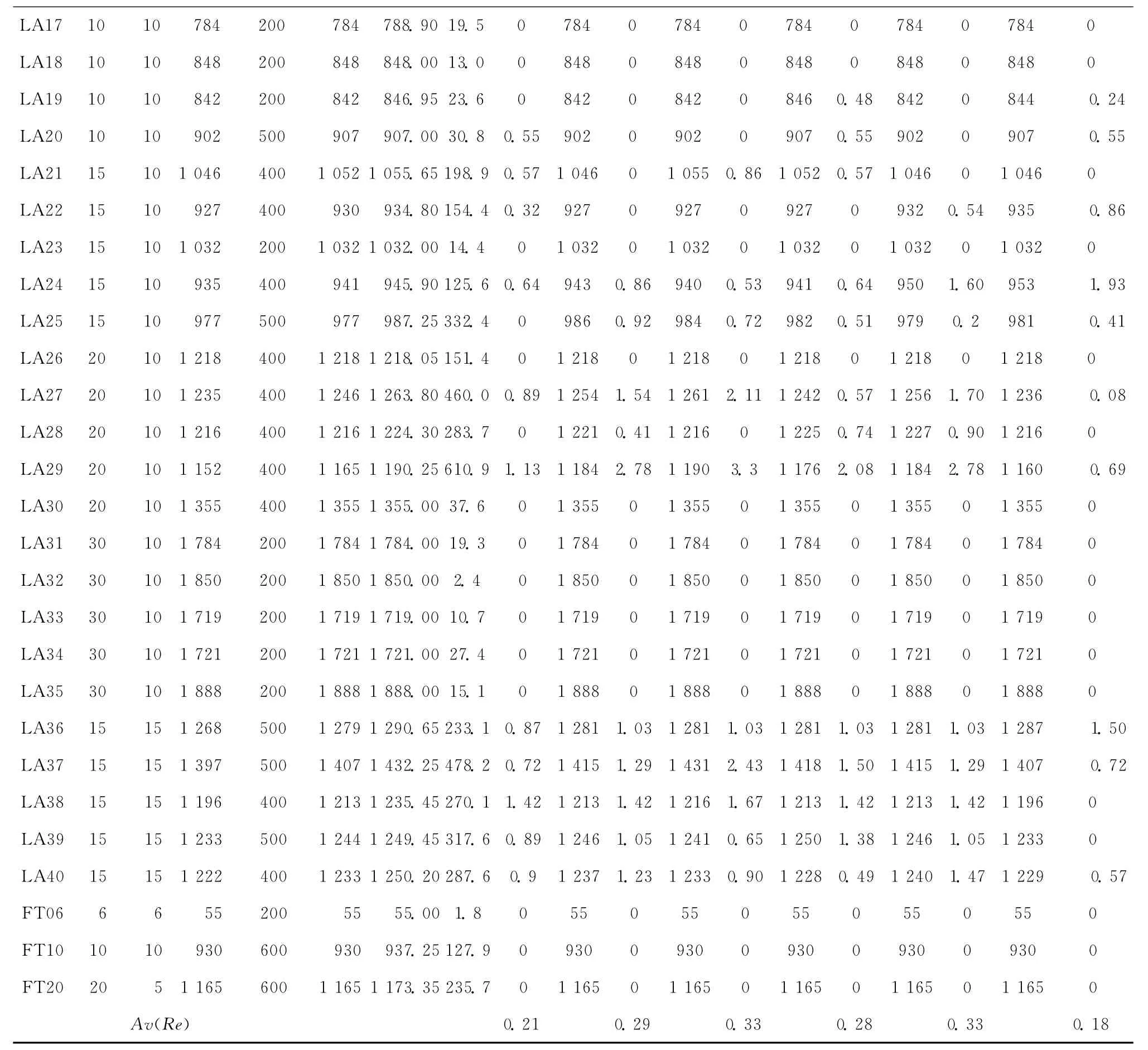
续表2

在算例求解优劣数目方面，将本文算法的最优解Cmax与5种算法分别进行对比统计分析，其中包括本文算法的优于解数目N1、差于解数目N2和相同解数目N3，统计结果如表3 所示。与文献［5］（2012）的混合遗传算法相比，优于解数目N1=5，差于解数目N2=6，算法性能基本相当。与文献［1-4］中的4种算法相比，优于解数目N1明显比差于解数目N2大，验证了本文算法性能的优越性。43个算例中，2个算例LA25和LA36的本文算法求解结果均优于文献中的5种算法，算例LA25的求解结果达到了已知最优解977，图11所示为本文算法对LA25和LA36算例求解结果的调度甘特图。

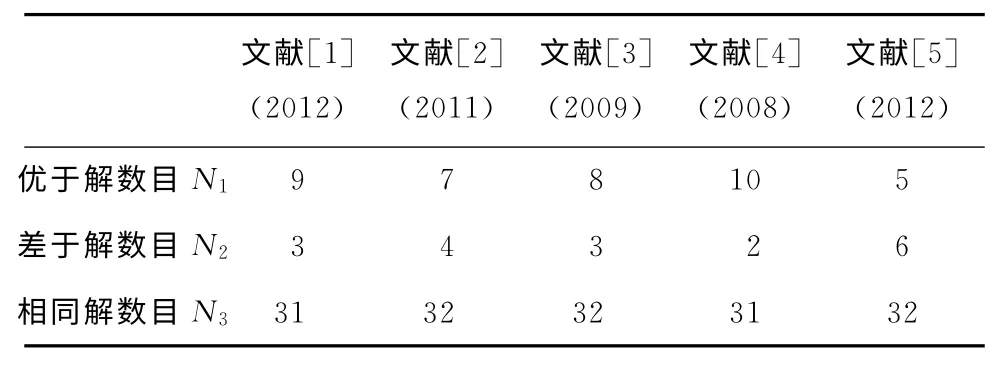
表3 优于解和差于解数目对比分析

4 结束语

本文针对最小化最大完工时间的JSP 优化问题，提出一种基于空闲时间邻域搜索的遗传算法，通过典型算例的测试结果验证了所提方法的有效性。本文的主要工作如下：

（1）分析了不同的解码方式，设计了一种基于空闲时间的邻域结构。

（2）给出同一台机器上任意两个工序位置相对移动时保证可行解的工序移动条件及证明，为进一步扩大工序的邻域搜索范围和设计新的邻域结构提供了理论基础。

（3）分析了同一机器上相邻两工序间的空闲时间，给出了最大限度查找属于关键工序的机器空闲时间方法，为更好地求解JSP提供了借鉴方法。

本文主要围绕作业车间调度问题共性关键技术进行研究，所取得的一些研究成果同样可以应用于其他智能算法，例如本文设计的邻域结构、保证可行解的工序移动条件理论等。通过与其他相关智能算法融合，算法的求解性能还有进一步提升的空间。

［1］ZUO X Q，WANG C L，TAN W.Two heads are better than one：an AIS-and TS-based hybrid strategy for job shop schedu-ling problems［J］.International Journal of Advanced Manufacturing Technology，2012，63（1-4）：155-158.

［2］GAO L，ZHANG G H，ZHANG L P，et al.An efficient memetic algorithm for solving the job shop scheduling problem［J］.Computers &Industrial Engineering，2011，60（4）：699-705.

［3］REGO C，DUARTE R.A filter-and-fan approach to the job shop scheduling problem［J］.European Journal of Operational Research，2009，194（3）：650-662.

［4］GE H W，SUN L，LIANG Y C，et al.An effective PSO and AIS-based hybrid intelligent algorithm for job-shop scheduling［J］.IEEE Transactions on Systems，Man，and Cybernetics-Part A：Systems and Humans，2008，38（2）：358-368.

［5］REN Q R，WANG Y P.A new hybrid genetic algorithm for job shop scheduling problem［J］.Computers &Operations Research，2012，39（10）：2291-2299.

［6］PAN Quanke，WANG Ling，GAO Liang，et al.Differential evolution algorithm based on blocks on critical path for job shop scheduling problems［J］.Journal of Mechanical Engineering，2010，46（22）：182-188（in Chinese）.［潘全科，王 凌，高 亮，等.基于差分进化与块结构邻域的作业车间调度优化［J］.机械工程学报，2010，46（22）：182-188.］

［7］YI Jun，LI Taifu.Bacterial foraging optimization algorithm based on variable neighborhood for job-shop scheduling problem［J］.Journal of Mechanical Engineering，2012，48（12）：178-183（in Chinese）.［易 军，李太福.求解作业车间调度的变邻域细菌觅食优化算法［J］.机械工程学报，2012，48（12）：178-183.］

［8］CUI Jianshuang，LI Tieke.Global neighborhood algorithm for job shop scheduling problem［J］.Computer Integrated Manufacturing Systems，2009，15（7）：1383-1388（in Chinese）.［崔健双，李铁克.求解作业车间调度问题的全局邻域搜索方法［J］.计算机集成制造系统，2009，15（7）：1383-1388.］

［9］ZHANG C Y，LI P G，GUAN Z L，et al.A tabu search algorithm with a new neighborhood structure for the job shop scheduling problem［J］.Computers &Operations Research，2007，34（11）：3229-3242.

［10］NOWICKI E，SMUTNICKI C.A fast taboo search algorithm for the job shop problem［J］.Management Science，1996，42（6）：797-813.

［11］BALAS E.Machine sequencing via disjunctive graphs：an implicit enumeration algorithm［J］.Operations Research，1969，17（6）：941-957.

［12］WANG Lei，HUANG Wenqi.A new local search algorithmfor job shop scheduling problem［J］.Chinese Journal of Computers，2005，28（5）：809-816（in Chinese）.［王 磊，黄文奇.求解工件车间调度问题的一种新的邻域搜索算法［J］.计算机学报，2005，28（5）：809-816.］

［13］ZHANG Chaoyong，GUAN Zailin，LIU Qiong，et al.New scheduling type applied to solving job-shop scheduling problem［J］.Chinese Journal of Mechanical Engineering，2008，44（10）：24-31（in Chinese）.［张超勇，管在林，刘 琼，等.一种新调度类型及其在作业车间调度中的应用［J］.机械工程学报，2008，44（10）：24-31.］

［14］BALAS E，VAZACOPOULOS A.Guided local search with shifting bottleneck for job shop scheduling［J］.Management Science，1998，44（2）：262-275.

［15］GRABOWSKI J，WODECKI M.A very fast tabu search algorithm for job shop problem［C］／／REGO C，ALIDAEE B.Metaheuristic Optimization via Memory and Evolution：Tabu Search and Scatter Search.Boston，Mass.，USA：Kluwer Academic Publishers，2005：117-144.

［16］GAO J，SUN L Y，GEN M.A hybrid genetic and variable neighborhood descent algorithm for flexible job shop scheduling problems［J］.Computers &Operations Research，2008，35（9）：2892-2907.