基于改进双向动态规划的立体图像匹配算法

程时文，林志贤，郭太良

(福州大学物理与信息研究工程学院，福建福州350000)

责任编辑:许 盈

立体匹配是计算机视觉领域的一个技术难题，其实质是在一定匹配约束条件下寻找同一目标图像在不同拍摄角度上相应像素点间的一一对应关系。从研究的现状来看，学者们提出了许多种立体匹配算法，根据匹配约束条件的差异性，可将立体匹配算法［1－2］分为两种，一种针对像素小邻域进行局部约束匹配的方法［3－5］，其特点是运行速度快、精度较高，但在遮挡区域的匹配效果较差;针对这一问题，一些学者提出了另一种全局匹配算法，即通过对整幅图像进行全局约束，相较而言，此类算法能够实现较低的误匹配率，但计算的复杂度较高。全局匹配算法主要包括:置信度传播(Belief Propagation，BP)［6－7］、动态规划(Dynamic Programming，DP)［8－11］、图 切割(Graph Cuts，GC)［12］等。此类匹配算法由于计算复杂度比较高，导致算法无法达到实时性的要求。因此在实时性要求较高的情况下，一般会选用DP算法，DP是全局算法中一种较典型的优化方法，它避免了非确定多项式(Non－Deterministic Polynomial，NP)问题，同时具有匹配效果良好、运行效率较高的特点。

但是，大部分DP算法有一个较为明显的不足，即视差图容易出现横向的“条纹”瑕疵，究其原因是缺少行、列方向上连续视差结果的融合。针对上述问题，诸多学者做了一些有建设性的研究。Birchfield等人［13］提出将竖直方向匹配度较高的区域视差拓展到低可信度区域的做法，该算法虽然实现了较快的运行速率，但扫描线间的视差结果较差，另外在算法优化部分可能会造成错误视差扩散到全局的不利影响;Gong and Yang［14］则提出了一种提高二通道DP算法可靠性的做法，即通过在垂直和水平两个方向上分别进行动态规划计算搜索路径，该算法确保了较高的匹配精度，但要借助编程图形显示卡来获取视差图的实时效果;另外Leung等人［15］提出了一种迭代动态规划(Iterative Dynamic Programming，IDP)算法，其通过多次迭代算法，来增强视差图的连续性，而导致的较长运行时间不利于实验操作。

鉴于此，本文提出一种基于改进双向动态规划的视差图获取算法，以修正后的ASCF为代价函数，并构建新的全局能量函数，通过改进双向动态规划寻径来得到最终的稠密视差图。经验证，所提算法的匹配效果良好，并获得了稠密视差图。

1 新型视差图获取算法的研究

DP算法的实质是将对应点的匹配问题转化为寻找某一能量函数的全局最优解，而构造出合适的像素间匹配的代价函数是构建全局能量函数的重要前提，所构建的代价函数优劣与否直接影响着立体匹配算法的运行速率和精确度，其中代价函数主要包含有差值绝对值和函数(Sum of Absolute Differences，SAD)、差值绝对值(Absolute Difference，AD)、差值平方 (Squared Differences，SD)等，此类代价函数在算法构造上相对简单、易于操作，但由于忽视了不同区域间跃变的影响，会产生较高的误匹配率。为了克服在交叉深度不连续区域的匹配问题，学者们在不连续区域为每一个像素选择自适应匹配窗口，其中Yoon等人［16］将几何数学的邻近性和像素色度空间融入到权值计算当中，此举有效地抑制了立体匹配中的不确定性，但在构建ASCF的过程中，导致视差非连续区域的误匹配率有所增加。

针对这一问题，提出了一种新型视差图获取算法即改进动态规划双向约束算法，即采用修正后的ASCF，进一步增强原始代价值在视差非连续区域的比重，以确保这一区域的误匹配率有所降低，从而改变构建ASCF的传统方法所导致总体误匹配率高的状况，并参照经典Potts模型［17］构建全局能量函数，考虑到相邻像素视差值保持的一致性准则，增加了视差平滑约束项的比重，提高所构建的全局能量函数的精确度。由于传统的DP算法在求取全局能量函数最优解时存在一个很大的局限性，即易出现“条纹”瑕疵的现象。为了克服这一问题，此算法提出采用扫描线行列双向动态规划来寻找最小匹配代价路径，并对初始视差图的数据项和平滑约束项分别制定了相应的奖励策略。最后，针对出现的错误孤立视差点，通过简单的滤波方法和遵循相关的3个准则予以消除。此算法流程如图1所示。

图1 算法流程

1．1 修正后的ASCF

Yoon等人［16］基于空间几何距离的相关性和像素间颜色相似性对ASCF进行了详细分析，即将几何数学的邻近性和像素色度空间融入到权值计算当中，其计算公式为

式中:γc和γp分别为控制权值的参数;Δgpq为对应像素的空间几何距离的相关性，即窗口中心像素p和匹配窗口中像素q之间空间坐标的欧几里德距离。

许多学者提出了不同的Δcpq构造方法，其中Salmen等人［18］根据像素点RGB值的内在联系，将Δcpq设定为窗口中心像素p与匹配窗口像素q的RGB值的加权欧几里德距离。由于获得该参数需要通过实验反复测试，以致代价函数的精确度相对较差，图像对的误匹配率也不低。Yang等人［19］对两像素点彩色差值求平均，尽管该构造方法在一定程度上减轻了算法的运算量，但由于忽略了像素点间彩色像素值的相关性，导致代价函数的自适应约束能力减弱，视差保持特性有所降低。

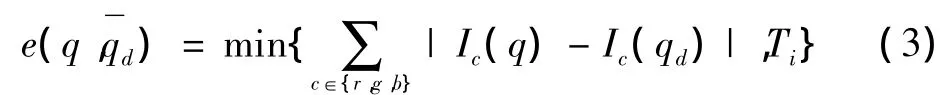
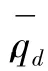
式中:Ti为截断门限值;Td为视差非连续区域的判断门限，当对应像素的彩色像素值差值的绝对值之和大于或等于在非连续区域的截断门限值时，原始代价值取为截断门限值，反之，取值为差值的绝对值与截断门限值之和中的最小值。

1．2 构建新的全局能量函数

本文构建的全局能量函数仍然只包含平滑项和数据项，其计算表达式如下

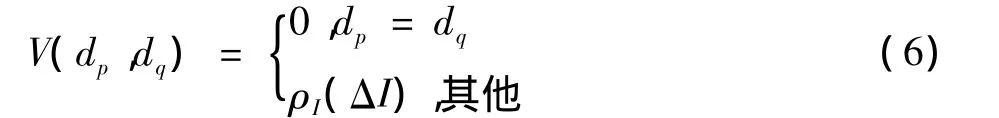
式中:ρI(ΔI)为相邻像素p与q之间的视差值。

梯度ΔI的函数ρI(ΔI)表达式为

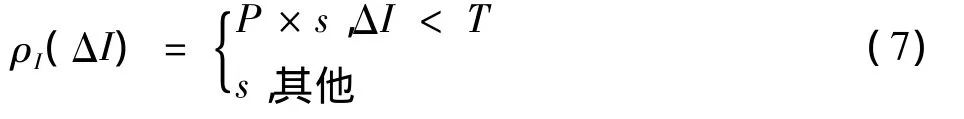
式中:s为惩罚项;T为阈值;P是用来增大梯度处的惩罚项。

在构建的新的全局能量函数中，针对平滑约束项作了以下修正

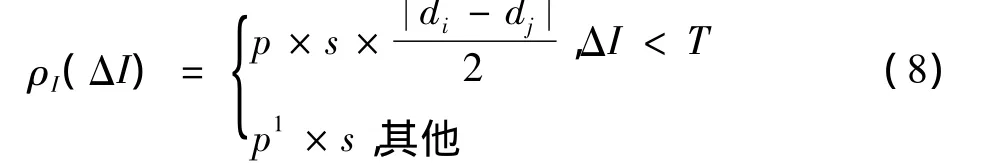
式中:p1为小于p的常参数。

1．3 改进双向动态规划寻径

由式(5)构建的新的全局能量函数可知，立体匹配问题转化为求解一个视差分配d*，即使能量函数E(d)的取值最小

图2 横向DP求解示意图

显然，这种缺少行、列方向上连续视差结果融合的DP算法不能保证全局最优，为了增强纵向像素间视差的约束项，以确保视差图横向条纹“瑕疵”的减少，故提出基于行、列双向的动态规划算法，具体过程如图3所示。

图3 行列双向DP示意图

本算法提出了一种由行匹配初试结果来确定相应的奖励策略，即通过减小d*所对应代价函数的比重，以提高其在列匹配中被选中的可能性，初始匹配结果依靠第一次行DP求解得到，同时需在确定的窗口区间内，对数据项制定了合理的奖励策略:情况1，若列方向初始视差梯度变化出现明显错误的视差值点时，其用原来的代价值来赋值;情况2，若在列方向初始视差梯度未出现异常的情况下，而在行动态规划中能够得到匹配的视差值点，那么其值应该赋予较大的奖励值;情况3，其他视差值点则使用较小的奖励值。其表达式为

式中:Ti为截断门限值，如式(4)所述;r一般取相对较小的正数，当r取值过小时，奖励值过小，会造成行方向上的DP效果不明显;当r取值过大时，会使得列方向上的视差值点被选中的概率过大，导致列方向上的DP失去了意义。经过多次实验测试得知，r取值为7时，所得匹配结果较为理想。另外，能量函数的数据项的计算方法与上述平滑项一致，这里就不再累述。

1．4 去除孤立的错误视差点

针对所获取视差图中出现的一些较为明显的噪声点，该算法采用易于操作的滤波方法来去掉孤立点。一般遵循以下3个可靠性准则:1)若该像素点上下邻域像素的视差值相等，则赋予该点视差值与上下邻域点一致;2)若该像素点左右邻域像素的视差值相等，则赋予该点视差值与左右邻域点一致;3)若该像素点周围邻域点的视差值都不相等，则赋予该点视差值为其邻域所有点的视差值均值。

2 实验结果

本算法的实验平台和参考图像来自于Middlebury大学数据库，对其中的 Cones，Venus，Tsukuba，Teddy 这 4幅图像进行了测试，实验中的各个参数k，γc，γp，Ti，Td，T ，p，r，s分别取值 1，5，19，25，30，5，3，10，3。实验结果如图4所示。此算法以修正后的ASCF为代价函数，并构建新的全局能量函数，通过改进双向动态规划寻径来得到最终的稠密视差图，分别与以ASCF作为代价函数、基于行列双向动态规划(DoubleDP)算法和以SAD作为代价函数的DP算法所获取视差图进行比较。实验视差图在所有区域(All)、非遮挡区域(Non_occ)、视差非连续区域(disc)的错误率做了记录，实验结果如表1所示。从表中分析可知，在优化策略一致的情况下，相较于SAD，采用ASCF来获取视差图误匹配率要低很多，而此算法相对于其他3种算法，误匹配率最低，“条纹”瑕疵方面最少，所获得的视差图效果最好。

图4 实验结果

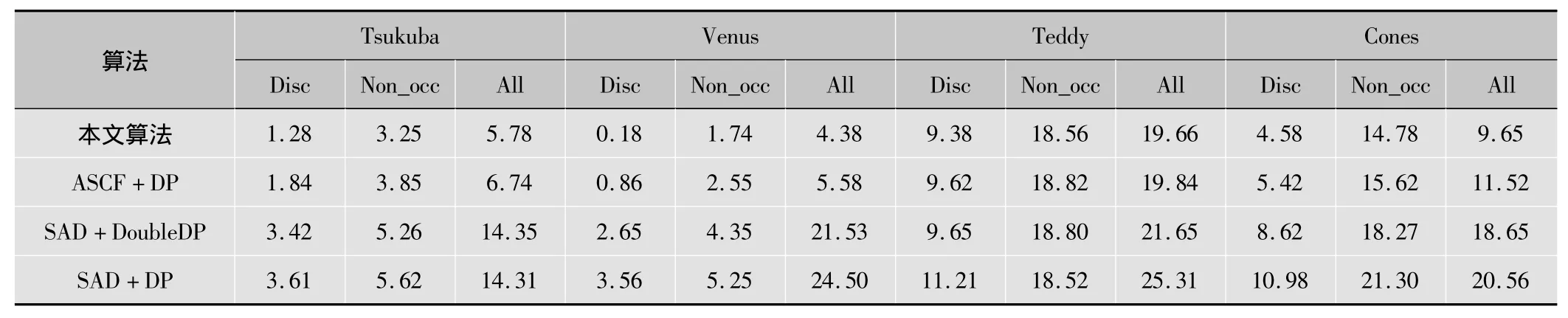
表1 不同算法之间的定量比较 %

3 小结

提出一种基于改进双向动态规划的视差图获取算法，以修正后的ASCF为代价函数，并构建新的全局能量函数，通过改进双向动态规划寻径来得到最终的稠密视差图。实验结果表明，该算法能够取得较为理想的效果，与其他3种DP算法相比明显降低了误匹配率，减少了图像中的“条纹”瑕疵。

虽然该算法在降低误匹配率和减少“条纹”瑕疵方面有显著的改善效果，但由于需要计算每个像素在确定窗口的自适应代价值，以致执行时间较长。故今后将使用GPU［21］和多线程［22］的处理方式，以便大幅度地提高算法运行速度，满足实际应用的要求。

［1］ SHIC B，WANG G J，PEIX K，etal．An interleaving updating framework of disparity and confidence map for stereo matching［J］．IEICE Trans．Information and Systems，2012(5):1552－1555．

［2］ FILHO G G．An optimal time－space algorithm for dense stereo matching［J］．Journal of Real－Time Image Processing，2012，7(2):69－86．

［3］吴文欢，李赛，江泽涛，等．基于局部不变特征的图像匹配算法［J］．计算机工程与应用，2012，48(14):168－170．

［4］ LIJ．An image feature point matching algorithm based on fixed scale feature transformation［J］．Optik－International Journal for Light and Electron Optics，2013，124(13):1620－1623．

［5］ ZHOU Y H，CHEN Y Q．Feature matching for automated and reliable initialization in three－dimensional digital image correlation［J］．Optics and Lasers in Engineering，2013，51(3):213－223．

［6］ XIANG X Q，ZHANG M M，LIG X，et al．Real－time stereo matching based on fast belief propagation［J］．Machine Vision and Applications，2012，23(6):1219－1227．

［7］ PEREZ JM，SANCHEZP，MARTINEZM，etal．Real－time stereo matching using memory－efficient Belief Propagation for high－definition 3D telepresence systems［J］．Pattern Recognition Letters，2011，32(16):2250－2253．

［8］ HU T B，QIB J，WU T，et al．Stereo matching using weighted dynamic programming on a single－direction four－connected tree ［J］．Computer Vision and Image Understanding，2012，116(8):908－921．

［9］ YU SC，YUX Y，HU L J，etal．Stereo matching for dynamic programming on TRIZ［J］．Information Technology Journal，2012，11(7):891－897．

［10］ CAI J．Integration of optical flow and dynamic programming for stereo matching［J］．IET Image Process，2012，6(3):205－212．

［11］ KALOMIROSJA，LYGOURASJ．Design and hardware implementation of a stereo－matching system based on dynamic programming［J］．Microprocessors and Microsystems，2011，35(5):496－509．

［12］ WANGD L，KAH B L．Obtaining depth map from segment－based stereo matching using graph cuts［J］．Journal of Visual Communication and Image Representation，2011，22(4):325－331．

［13］ BIRCHFIELD S．Depth discontinuities by pixel－to－pixel stereo［J］．International Journal of Computer Vision，1999，35(3):269－271．

［14］ GONG M，YANG Y H．Near real－time reliable stereo matching using programmable graphics hardware［C］//Proc．Conference on Computer Vision and Pattern Recognition．San Diego，CA:IEEE Press，2005:924－931．

［15］ LEUNG C，APPLETON B，SUN C M．Iterated dynamic programming and quadtree subregioning for fast stereo matching［J］．Image and Vision Computing，2008，26(10):1371－1380．

［16］ YOON K J ，KWEON IS．Locally adaptive support－weight approach for visual correspondence search［J］．IEEE Computer Society Conference on Computer Vision and Pattern Recognition，2005(2):924－931．

［17］ BOYKOV Y，VEKSLERO，ZABIH R．Fast approximate energy minimization via graph cuts［J］．IEEE Trans．Pattern Analysis and Machine Intelligence，2001，23(11):1222－1239．

［18］ SALMEN J，SCHLIPSING M，EDELBRUNNER J，et al．Real－time stereo vision:making more out of dynamic programming［C］//Proc．13th International Conference on Computer Analysis of Images and Patterns，Munster，Germany:IEEE Press，2009:1096－1103．

［19］ YANG Q X，WANG L，YANG RG，et al．Stereo matching with color weighted correlation，hierarchical belief propagation and occlusion handling［J］．Computer Vision and Pattern Recognition，2006，12(2):2347－2354．

［20］赵明，李晓白，郎荣玲．行列双动态规划的改进自适应立体匹配算法［J］．计算机工程与应用，2011，47(23):177－180．

［21］刘金硕，刘天晓，吴慧，等．从图形处理器到基于GPU的通用计算［J］．武汉大学学报:理学版，2013，59(2):198－206．

［22］蔡雨辰，赵保军，邓宸伟．实时信息处理系统多线程框架的高效设计方法［J］．高技术通讯，2013，23(1):42－48．