发射装药非稳态温度场仿真

邹 嘉，纪京新

(1.海军装备部西安军事代表局，陕西 西安 710100;2.海军工程大学，湖北 武汉 430033)

弹药在长期贮存过程中，环境温度对发射药性能影响很大。温度过高，会使发射药的热分解、水解和氧化氮自催化作用加速，可能造成发射时燃速加快，膛压、初速上升;温度过低，会使发射药的机械强度降低，在受外力作用下，容易破裂使表面积增大，发射时造成燃速增大，影响射击精度;弹药射击时，其药温相差1℃，引起弹丸初速误差大约1m/s，导致弹着距离偏差50m［1-2］。此外，温度的变化，也会引起湿度的变化，研究表明，当相对湿度在65% ～70%，气温下降至6℃时，会出现结露［3］。可见，获取实时准确的发射药的温度场分布，具有一定的军事价值，可以为弹药的长期贮存和装药失效分析提供参考。但在实际中，不允许对弹药进行破坏性的开孔［2］，这就给温度的获取带来了困难。

本文借助Ansys软件的热分析功能，对发射装药非稳态温度场仿真，不仅可以对发射药温度和环境温度变化情况进行分析，也可以节省大量的费用，对弹药发射装药的贮存规律、失效机理及射击试验具有一定的参考价值。

1 非稳态热分析原理

非稳态热分析用于计算一个系统的随时间变化的温度场及其它热参数。在工程上一般用非稳态热分析计算温度场。非稳态热分析中的载荷是随时间变化的。为了表达随时间变化的载荷，首先必须将载荷-时间曲线分为载荷步。对于每一个载荷步，必须定义载荷值及时间值，同时必须选择载荷步为渐变或阶越。

非稳态热分析中，系统的温度、热流率、热边界条件以及系统内能随时间都有明显变化［4］。根据能量守恒原理，以矩阵形式表示的非稳态热平衡为

式中，［K］为传导矩阵，包含导热系数、对流系数及辐射率和形状系数;［C］为比热矩阵，考虑系统内能的增加;{T}为节点温度向量;{˙T}为温度对时间的导数;{Q}为节点热流率向量，包含热生成。

2 模型的建立

2.1 仿真模型的建立

本文以典型的3种(小、中、大)口径弹药为例。选择PLANE55四边形4节点轴对称单元，用二维热传导进行分析。以弹药发射装药径向截面建立二维模型，外层为弹药药筒，内层为发射药，由于弹药横向截面是轴向对称结构，为便于仿真，本文选取1/4截面为研究对象，见图1。材料的力学参数如表1所示［5-6］，本文以双基药为例进行温度场的仿真，对其它发射装药可以通过改变材料的热力学参数实现其温度场的仿真。

表1 材料参数

2.2 初始条件和边界条件

弹药在贮存过程中的温度变化是由于弹药表面与周围环境温度之间存在温差，从而引起热量交换，主要分为自然对流和强制对流。自然对流的传热系数为1-10w/(m2·k)，主要是由于空气温度冷热分布不均引起的;强制对流为10-100w/(m2·k)，主要是由于压差作用引起的［5］。弹药在贮存过程中，其外界温度是变化的，在实际业务工作当中，一天内通常是测定几个时刻的温度，因此，假定两相邻时刻之间的温度呈线性变化;弹药在进行射击试验之前，通常要对弹药进行保温，使其药温基本趋于一致，其环境温度基本不变。基于上述两种考虑，本文设定的边界条件主要有恒温和线性变化的温度两种环境条件。

3 发射装药温度场求解

弹药在贮存和试验条件下，通常关心装药温度变化最快的节点和装药整体温度趋于一致的时刻，所以，选择装药外表面和中心两个节点作为对象研究其温度场分布情况。以环境温度与装药轴心温度的温差到达某一温度范围表示温度平衡时刻，以装药外边面温度到达一定值时表示温度对装药的影响。

3.1 不同传热方式下的装药温度场仿真

假设弹药在自然对流条件下的其表面传热系数为5 w/(m2·k)，在强制对流条件下的表面传热系数为40 w/(m2·k)，环境和弹药初始温度为15℃，环境温度在2.5h内变化至25℃，选取中口径弹药，设置时间为 9000s(2.5h)，步长为 50s，通过仿真得到 2.5h 内弹药两个节点的温度变化和终点时刻的温度场分布，如图1～4所示。

通过温度场云图和温度变化曲线图可以看出，经过2.5h仿真后，强制对流装药外边面温度上升至24℃以上，而自然对流装药外边面温度上升至不到20℃;自然随流下装药温度变化曲线较强制对流平缓。可以得出，在同样的环境温度下，强制对流较自然对流对装药的温度影响较大，各节点温度随着装药外边面到轴心的深入逐渐平缓。

图1 自然对流2.5h后温度场云图

图2 强制对流2.5h后温度场云图

图3 自然对流两节点随时间变化图

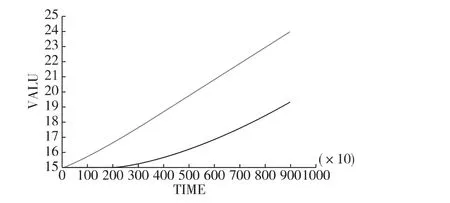
图4 强制对流两节点随时间变化图

3.2 恒温条件下的装药温度场仿真

假设在自然对流条件下，选取中口径弹药，弹药初始温度为15℃，环境温度分别为6℃、25℃和30℃，设置时间为90000s，步长为100s，得到不同环境温度下两个节点的温度变化。以发射装药轴心与环境温度相差0.01℃为平衡温度，则三种口径弹药到达平衡温度的时间如表2所示，图5为环境温度为6℃时的装药温度随时间变化曲线图。

表2 不同环境温度下到达平衡温度时间表

图5 环境温度为6℃装药随温度变化曲线图

通过仿真，可以看出装药温度变化情况与环境温度有关，但是升温或者降温过程的总体趋势基本相同，只不过当温差较大时前期曲线变化较快，后期变化较为平稳。通过表2和图5可以看出，对于同口径弹药，当环境与装药温差较大时，达到平衡温度的时间也较大，但是温差对装药到达平衡温度的时间影响不大，对中口径弹药，经过20h的传热，装药温度与环境温度相差小于0.1℃。

3.3 不同口径弹药的装药温度场仿真

假设在自然对流条件下，弹药初始温度为15℃，环境温度为25℃，设置时间为90000s(25h)，步长为100s，得到三种不同口径弹药两个节点的温度变化情况。以发射装药外表面与环境温度相差0.01℃为平衡温度，则三种口径弹药到达平衡温度的时间如表3所示。

表3 不同口径弹药到达平衡温度时间表

从表3可以看出，随着弹药口径的增大，到达平衡温度的时间也逐渐增大，对于大口径弹药，至少经过1.492天才能到达平衡温度，对于小口径弹药，则需要经过至少6.9小时。

3.4 变温条件下的装药温度场仿真

弹药在实际贮存当中，当环境温度有上升至30℃以上的趋势时，往往会采取合理的措施进行降温，因此，弹药库房的温度通常是周期性变化的。假设某弹药库房温度在15℃ ～25℃内周期变化，时间间隔为4小时，表面传热方式为自然对流，弹药口径为76mm，发射药初始温度为15℃。得出在此条件下的装药温度场变化情况如图6所示。

图6 变温条件下装药温度随时间变化曲线

通过温度变化曲线图可以看出，装药外表面温度波动较大，中心较为平缓，在装药内侧的温度迟于外侧。随着时间的增长，其装药温度最终将会趋于平衡状态，即在某一阈值范围内波动。

4 结束语

本文通过对弹药发射装药非稳态温度场的仿真，可以得出发射装药温度场的变化规律，为弹药的贮存和实验提供一定的参考价值。文中对不同传热方式、不同环境温度和不同口径的弹药进行温度场仿真，通过比较可以看出，弹药装药温度变化情况从装药外边面至中心逐渐趋于平缓，从传热方式来看，强制对流较自然对流对于弹药装药内部传热影响更大;装药与环境温差较大的情况下，初始时刻装药温度变化越快，但是，到达平衡温度的时间相差不大;弹药口径对传热影响较为显著，口径越大，传热到达平衡温度时间越长。

综上所述，在弹药的长期贮存时，应注意保持通风，加速空气流动，但是当环境温度过高时，通风时间不宜过长;弹药试验前，应根据弹药口径不同，合理确定保温时间。

［1］ 唐寿江.温度对弹药质量变化的影响［J］.湖北科技学院学报，2013，33(7):187-188.

［2］ 陆欣，周彦煌.火炮发射药非稳态温度场的试验与数值计算［J］.弹箭与制导学报，2003，23(1):190-195.

［3］ 番文庚.温度和电磁环境对航弹失效影响分析［D］.南京:南京理工大学，2008.

［4］ 邓凡平.Ansys10.0有限元自学手册［M］.北京:人民邮电出版社，2007.

［5］ 番文庚，王晓明，陈瑞，等.航空弹药贮存环境温度场仿真研究［J］.系统仿真学报，2008，20(12):3258-3261.

［6］ 陈明华，江劲勇，路桂娥，等.GF-A0066320G弹药长期贮存后发射药剩余能量的计算［R］.石家庄:军械工程学院，2009.