含双馈感应电机风电场的动态等值

刘正楷，俞 慧，何 芳

(国网铜陵供电公司，安徽 铜陵 244000)

0 引言

近年来，风力发电极为快速，对电力系统稳定性影响越来越大。含双馈感应发电机风电场，主要组成部分包括双馈发电机、风力机(叶片，联轴器，齿轮箱)、变流器及控制系统和风电场出口处的升压变压器等。双馈电机一般用三阶或五阶微分方程予以描述［1～3］。风力机传动系统用二阶或者三阶微分方程描述［3～5］，加上变流器及控制系统［5］，使得暂态稳定计算中所用的微分方程数量很多。实际大型风电场包括很多台风电机组，因此详细模型仿真计算时间长，计算量大。研究风电系统暂态稳定特性时，一般并不需要严格区分风电场中每台机组贡献，因此可将由风电场动态等值为一台风电机组处理以节省计算量。

双馈感应风电机组的等值算法，包括风力机及其传动部分的机械特性、以及感应电机及其变流器的机电特性。从风力机侧考虑，可根据风速［6～9］、风力机转速［10］、或浆距角控制［11］，对机组进行分群，把分群参数近似的风电机组进行等值。从感应电机侧，文献［12，13］通过聚合电磁功率或输入双馈电机的机械转矩对双馈电机部分等值，未计及风力机部分。文献［14］认为等值风速为所有单台风机风速的平均值，进而对整个风电场进行等值。但由于风力机捕捉机械功率与风速并不成简单比例关系，因此该方法存在一定误差。文献［15，16］通过查找风速-功率曲线找到等值后的风速，并且通过聚合电磁功率或输入双馈电机的机械转矩来等值风电场，这种方法对风速在额定风速以下的风机适用，当风速大于额定风速时无法从曲线上查找风速。

本文对于不同风速不同型号的风电机组，从风速等值开始，逐步对整个风电系统各个部分进行详细等值。首先根据风电机组的两种不同运行状态对风场风速进行等值，由等值后风能利用系数求出等值后的浆距角，再由转矩平衡求出等值后的初始风力机角速度和初始运行滑差，最后运用按容量加权求和的等值方法对双馈电机、变流器及控制系统参数进行等值。采用电网短路故障及风速变化时两种情况，比较了等值前后风场出口处电压、有功功率和无功功率、以及同步发电机功角和频率的变化曲线和等值误差。误差分析和计算效率验证了等值算法的应用价值。

1 双馈感应风力发电系统的数学模型

1.1 风力机与传动系统模型

风力机通过叶片捕获风能，将风能转换为作用在轮毂上的机械转矩。风力机通过风速获取的机械功率Pw见(1)式［4］，其中ρ为空气密度;R为叶片半径;Vw为风速;叶尖速比λ=ωtR/Vw，ωt为风力机角速度。

当实际风速高于额定风速，由于风力发电机组机械和电气安全限制，需要控制转速在限定值以下，输出功率保持不变。增大风机桨叶节距角可以使发电机的输出功率下降，使转速保持在限定值以内，因此一般高风速时采用浆距角控制［17］，图1中ωtef为转速参考值，βmin和βmax分别为浆距角可调的最小角度和最大角度。

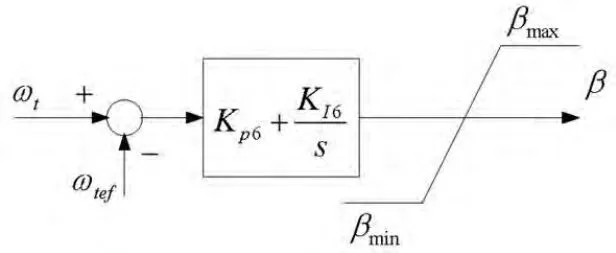
图1 浆距角控制

传动系统包括涡轮、齿轮箱、联轴器以及风力机的其他机械部分，通常用两阶模型表示［3～5］(3)～(5)式

其中Ht为风力机的惯性时间常数;ωr为发电机转子角速度;ωs为发电机定子角速度;θtw为轴扭转角度;Ksh为轴刚度系数;Dsh为阻尼系数;sr为双馈发电机转差;Tm为输入双馈发电机转矩;Tw为风力机叶片输出转矩，Tw=Pw/ωt。

1.2 双馈感应发电机模型

当发电机转子转速变化较大时，转子磁链增量对发电机动态过程的影响，远大于定子磁链增量影响，因此在研究双馈发电机动态过程中，可忽略定子磁链暂态，双馈感应发电机采用如下5阶模型(6)～(8)式。

其中Hg分别为双馈发电机的惯性时间常数;Te为感应发电机电磁转矩，Te=Pe/ωs，Pe为双馈发电机电磁功率和分别为双馈电机暂态电势的d轴和q轴分量=Xrr/Rr为转子回路时间常数;=Xs+XrXm/(Xr+Xm)为发电机等效暂态电抗;Udr和Uqr为双馈电机转子电压的d轴和q轴分量;Ids，Iqs，Idr，Iqr为双馈电机定子电流和转子电流的 d 轴和 q轴分量;Xss=Xs+Xm，Xrr=Xr+Xm=Xrr－XmXm/Xss，Rs，Rr，Xs，Xr分别为双馈电机定子电阻，转子电阻，定子电抗和转子电抗;为双馈电机定子电压。

1.3 变流器及其控制模型

转子侧变流器用来控制电机输出有功以跟踪风力机输入功率，并控制电网侧电压或无功。其控制框图见图 2［5，18］，其中 Pg、Qg、Pref、Qref分别为双馈电机注入电网的有功和无功功率、以及有功和无功参考值。

式中，ωtr为风力机的额定角速度;Pwr为额定角速度下风力机输入的额定功率;Qgr为双馈电机注入电网的额定无功功率。

图2 转子侧变流器控制

图3 网侧变流器控制

网侧变流器与转子侧变流器通过直流环节连接，其数学模型见(10)式，其中R，L为变流器交流侧进线电抗器的电阻和电感;Cf为直流环节直流电容，vdc为其直流电压;ud，uq，vd，vq分别为变流器交流侧电压和电网电压的d轴、q轴分量;id，iq为变流器交流进线流过电流的d轴、q轴分量。

直流电压vdc恒定是背靠背变流器稳定工作的前提。网侧变流器控制目标为直流电压恒定，并控制网侧变流器输入电网无功，其控制框图如图3，其中vdc_ref为直流参考电压;id_ref，iq_ref为变流器交流进线流过电流的d轴、q轴分量参考值，iq_ref一般取零。

从上述模型可知，感应电机风电机组的动态模型，包括至少18个微分方程，以及部分代数方程。考虑到大型风场的风机阵列，微分方程数非常庞大。因此，如果研究对象不是个别风电场而是风电系统同步电机暂态稳定特性时，有必要风场内双馈感应电机等值为一台。

2 动态等值算法

若一个风电场包括N台风力发电机，则合成等值机的容量、风力机捕获的机械功率分别为各台风力发电机的容量、风力机捕获的机械功率之和，如式(11)，其中下标eq表示等值机。

则以等值机容量为基准容量的等值风力机捕获的机械功率标幺值P*weq如式(12)，

2.1 风力机的等值

假设加在每台风机上风速为Vwj(j=1，…，N)，风场额定风速为Vwr，切入风速为Vin，切除风速为Vout。对于每一台风机，若Vin≤Vw≤Vwr，则风力机运行在Cp恒定区，采取速度控制策略进行最大功率追踪;若Vwr＜Vw≤Vout，则风力机运行在功率恒定区，采取功率控制策略保持功率恒定。根据风力机的两种不同运行状态，分两种情况对风力机进行等值。

(1)若max(Vwj)≤Vwr，j=1，…，N，则等值机运行在Cp恒定区，在这种情况下，等值后的风能利用系数Cpeq，等值叶片半径Req和等值风速Vweq如式(13)，

式中，Cpmax为风能利用系数最大值。

(2)若min(Vwj)＞Vwr，j=1，…，N，则等值机运行在功率恒定区，在这种情况下，等值后的风能利用系数Cpeq，等值叶片半径Req和等值风速Vweq如式(14)

对于浆距角控制系统，首先计算等值后的叶尖速比λeq=ωteqReq/Vweq，然后分别联立风力机两种不同运行状态下等值后的Cpeq，求解(2)式可得到两种不同运行状态下的等值浆距角βeq。

2.2 传动系统与双馈电机的等值

由稳态时微分方程式(3)和式(6)等于零即转矩平衡，可得Te=Tm=Tw，则等值后的风力机转速ωteq和双馈电机初始运行滑差sr0eq如式(15)

根据加权求和法［19］，求等值后传动系统参数式(16)～(17)，

式中权系数ρj=SGj/SGeq是第j台双馈电机的容量在总容量中所占的比重。Hteq和Hgeq分别为风力机和发电机的等值惯性时间常数;Ksheq、Dsheq为等值后轴刚度系数和阻尼系数。

按容量加权求和法求得双馈电机等值后参数如式(18)～(20)，

2.3 变流器及控制系统的等值

对于网侧变流器模型，要保持等值前后直流环节直流电压保持恒定，其等值后的参数如式(21)

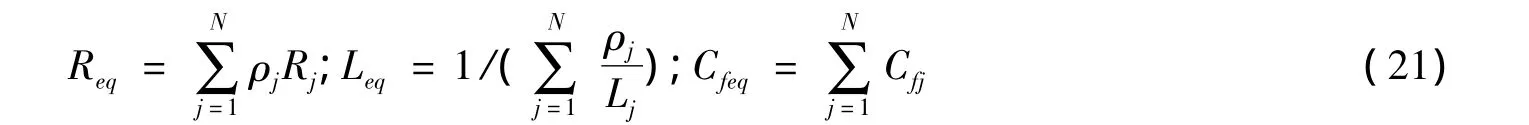
对于变流器控制系统，要保持等值前后其控制目标保持不变，其等值后PI调节器参数如式(22)

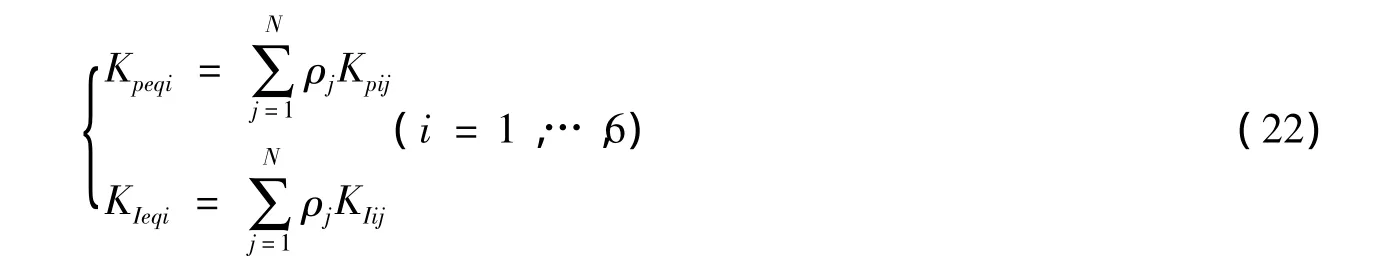
3 算例分析

本文采用MATLAB语言，独立编程实现上述所有算法。算例采用IEEE新英格兰39节点测试系统，增加一个风场节点(图4)。风电场由5排10列共50台风机，每排包含5台2MW机组和5台1.5MW机组。风场额定风速为13m/s，通过各风机风速相互独立。本文假设通过每排的风速依次递减0.5m/s。

图4 IEEE39节点测试系统

以下检验输电线路短路和风场风速扰动后的动态等值效果，其中故障模式为电网线路中F点在1s时发生单相接地短路，1.2s时故障结束。采用四阶龙格-库塔法解微分方程，步长0.01s。总仿真周期为10s。

定义平均相对误差ε为两条曲线采样点φ之差的2-范数除以采样点数目Ω:

3.1 风速小于额定风速状态

当风电场风速小于额定风速时，假设通过风电场第一排的风速为13m/s，则按照上述算法算得等值后风速为12.0617m/s。图5给出了此种状态下，电网发生单相接地短路故障时，等值前后风电场出口处母线电压、注入电网有功功率和无功功率、节点30、31上同步发电机功角差，以及节点31同步发电机频率的变化曲线。等值前后风电场出口参数及电网参数平均相对误差见表1中ε1。

图5 电网故障时风场和同步电机参数

由图5可见，风速在额定风速以下，给定故障模式和切除时间下，系统能保持暂态稳定。对比等值前后曲线以及表1中ε1可以看出，等值前后风电场出口处参数变化趋势基本一致，平均相对误差很小，吻合精度高，验证了算法的精确性。运用等值算法，等值前系统暂态稳定仿真时间为72.4s，等值后系统仿真时间为16.2s，可见等值算法大大缩短了计算时间。

图6给出了随机风扰动下，等值前后风速及风场出口处注入电网的有功和无功功率变化曲线。风速扰动时风电场出口参数平均相对误差如表1中ε2。

由图6可见，风场风速扰动时，等值前后风电场出口处参数变化曲线基本一致，吻合程度高。由表1中ε2也可以看出等值前后曲线误差很小，精度高，验证了等值算法的准确性。

图6 风速扰动时风场出口参数

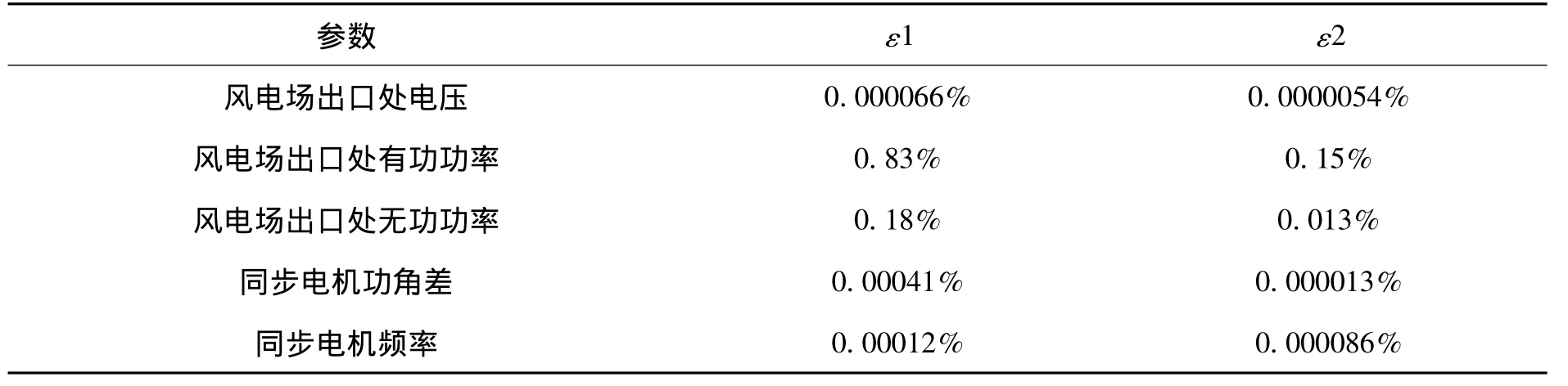
表1 风速小于额定风速时等值误差

3.2 风速大于额定风速状态

当风电场风速大于额定风速时，假设通过风电场第一排的风速为16m/s，则按照上述算法算得等值后风速为14.9583m/s。图7给出电网故障时，等值前后风电场出口处母线电压、注入电网有功功率和无功功率、电网中节点30和31上同步电机功角差、以及节点31同步电机频率的变化曲线。风电场出口参数和电网参数误差如表2中ε1。

由图7可见，风速大于额定风速时，电网发生扰动且及时切除故障，系统能保持暂态稳定。由表2以及图7可见，风速大于额定风速时，电网发生故障，风电场出口参数和电网参数等值前后变化趋势基本一致，曲线误差很小，等值精度高，验证了算法的有效性。运用等值算法，等值前系统暂态稳定仿真时间为75.9s，等值后系统计算时间为16.6s。

图7 电网故障时风场和同步电机参数

图8给出了风场随机风扰动时，等值前后风速及风场出口处注入电网的有功和无功功率的变化曲线，其等值前后误差如表2中ε2。

比较图8可以看出，在风场风速大于额定风速的情况下，风电场发生风速扰动，等值前后风电场出口处参数变化曲线趋势基本一致，吻合程度高。由表2中ε2也可以看出等值前后曲线误差很小，验证了等值算法的有效性。

图8 风速扰动时风场出口参数

表2 风速大于额定风速时等值误差

4 结论

本文提出并实现了一种含双馈感应电机风电场的等值算法，主要特点如下:

(1)等值范围包括风力机及其传动系统的机械特性，以及感应电机及其驱动系统的机电特性。考虑风速在额定值以下或以上时，风力机采取速度控制和功率控制策略，分两种情况等值风速和风能利用系数。

(2)从风电系统暂态稳定角度出发，等值前后结果包括风场出口参数(电压、有功、无功)，以及其他同步发电机的功角和频率。等值后各参数平均等值误差均小于1%，计算时间约为等值前的1/4。

目前仅研究了风速在额定风速以上或以下扰动时的等值情况。对于风速由额定风速以上/以下突变到额定风速以下/以上，即风力机控制策略在速度控制和功率控制两者之间变换时，等值效果较差，仍有待进一步研究。

附录

A.2MW风力发电机组参数:

Ht=3.5s，Hg=0.9s，Ksh=0.9p.u./el.rad，Dsh=34

Rs=0.00488，Xs=0.09241，Rr=0.00549，Xr=0.09955

Xm=3.9527，R=0，L=0.08，Cf=5000μF，Vdc=1200V

Kp1=1.8，KI1=5.1，Kp2=0.3，KI2=0.5，Kp3=1.0，KI3=5.3

Kp4=1.2，KI4=0.5，Kp5=2.5，KI5=1.2，Kp6=400，KI6=600

B.1.5MW风力发电机组参数:

Ht=3.0s，Hg=0.7s，Ksh=0.8p.u./el.rad，Dsh=29.5

Rs=0.00336，Xs=0.0868，Rr=0.00304，Xr=0.1243

Xm=4.7014，R=0，L=0.05，Cf=3000μF，Vdc=1200V

Kp1=1.9，KI1=5.0，Kp2=0.3，KI2=0.4，Kp3=1.1，KI3=4.9

Kp4=1.3，KI4=0.4，Kp5=2.5，KI5=1.1，Kp6=400，KI6=500

［1］李生虎，刘正楷，杨振林.风电系统中异步电机机电模式研究［J］.电力系统保护与控制，2010，38(21):44-50.

［2］Andres F，Jose C，Camilo C.A third order model for the doubly-fed induction machine［J］.Electric Power Systems Research，2000，56(2):121-127.

［3］Mei F，Pal B C.Modeling and small-signal analysis of a grid connect double-fed induction generator［C］.IEEE Power Engineering Society General Meeting，2005，3:2101-2108.

［4］Li S H，Liu Z K，Hao X J，et al.Dynamic equivalence to induction generators and wind turbines for power system stability analysis［C］.The 2nd International Symposium on Power Electronics for Distributed Generation Systems，2010:887-892.

［5］Wu F，Zhang X P，Keith G，et al.Modeling and control of wind turbine with doubly fed induction generator［C］.Power Systems Conference and Exposition，2006:1404-1409.

［6］Nunes M V A，Pecas L J A，Zurn H H，et al.Influence of the variable-speed wind generators in transient stability margin of the conventional generators integrated in electrical grids［J］.IEEE Transaction on Energy Conversion，2004，19(4):692-701.

［7］Usaola J，Ledesma P，Rodríguez J M，et al.Transient stability studies in grid with great wind power generation.Modelling issues and operation requirements［C］.IEEE Power Engineering Society General Meeting，2003，3:1534-1541.

［8］黄梅，万航羽.在动态仿真中风电场模型的简化［J］.电工技术学报，2009，24(9):147-152.

［9］苏勋文，米增强，王毅.风电场常用等值方法的实用性及其改进研究［J］.电网技术，2010，34(6):175-180.

［10］米增强，苏勋文，杨奇逊，等.风电场动态等值模型的多机表征方法［J］.电工技术学报，2010，25(5):162-169.

［11］米增强，苏勋文，余洋，等.双馈机组风电场动态等效模型研究［J］.电力系统自动化，2010，34(17):72-77.

［12］Fernández L M，Jurado F，Saenz，J R.Aggregated dynamic model for wind farms with doubly fed induction generator wind［J］.Renewable Energy，2008，33(1):129-140.

［13］Shafiu A，Lara O A，Bathurst G，et al.Aggregated wind turbine models for power system dynamic studies［J］.Wind Engineering，2006，30(3):171-186.

［14］Fernández L M，García C A，Saenz J R，et al.Equivalent models of wind farms by using aggregated wind turbines and equivalent winds［J］.Energy Conversion and Management，2009，50(3):691-704.

［15］Yang Y B，Zha X M.Aggregating wind farm with DFIG in power system online analysis［C］.IEEE 6th International Power Electronics and Motion Control Conference，2009:2233-2237.

［16］Fernández L M，García C A，Saenz J R，et al.Reduced model of DFIGs wind farms using aggregation of wind turbines and equivalent wind［C］.IEEE Mediterranean Electro technical Conference，2006:881-884.

［17］Lin L，Zhang J，Yang Y H.Comparison of pitch angle control models of wind farm for power system analysis［C］.Power＆ Energy Society General Meeting，2009:1-7.

［18］赵仁德，贺益康，黄科元，等.变速恒频风力发电机用交流励磁电源的研究［J］.电工技术学报，2004，19(6):1-6.

［19］鞠平，马大强.电力系统负荷建模［M］.北京:中国电力出版社，2008.