充填钻孔寿命SVM优化预测模型研究

张钦礼，陈秋松，胡威，高瑞文

(中南大学 资源与安全工程学院，湖南 长沙，410083)

如何在环境不受破坏的前提下，合理、高效地利用矿产资源是当今社会和各界的关注重点，充填采矿法由此应运而生。充填采矿法不但能提高采矿回收率，有效降低了贫化率，而且为回收难采矿产资源和边界经济矿产资源等提供了可能[1−2]。此外，充填采矿法还能有效控制并降低采场地压，防止大规模岩层移动、矿岩整体失稳、巷道顶板突发性冒落以及岩爆、冲击地压等发生。但充填采矿法也存在一些难题，特别是地下矿山进行充填时存在充填钻孔的使用寿命问题。充填钻孔作为充填料浆的专属通道，承受了料浆的腐蚀与冲刷作用，容易造成破损堵塞。一旦充填钻孔破坏，要恢复基本不可能。而充填钻孔被损坏必然影响矿山的充填和采矿工艺的衔接，甚至会影响矿山正常的生产：因此，对充填钻孔的寿命进行预测，提前对钻孔进行修复，是维护矿山正常生产的重要环节，具有重大的意义[3]。目前比较常见的预测分析方法主要有回归分析法、神经网络法[4−6]等。回归分析法主要用于变量关系简单、易找到关系方程的模型，在技术条件复杂的矿山充填系统中显然不太适用。神经网络法应在许多复杂的模型中得到运用。郑晶晶等[7]采用BP神经网络对充填钻孔寿命进行了预测，在一定程度上取得了良好效果。但神经网络的局部极小点、过学习以及结构和类型的选择过分依赖于经验等固有的缺陷，严重降低了其应用和发展的效果。支持向量机能有效克服神经网络的这些缺陷[8]。与神经网络不同，支持向量机(SVM)是一种基于结构风险最小化原则的新型回归方法，并且是在小样本情况下发展起来的统计机器学理论，在很多情况下可以克服维数灾难问题。为此，本文作者针对充填钻孔寿命预测问题，运用SVM进行建模，而针对困扰SVM的模型参数选择问题，结合遗传算法(GA)进行优选，确保所选参数最优化，从而使模型最优化。由此得到的模型可以保证对充填钻孔寿命预测的准确性。

1 支持向量机回归数学模型

SVM[9−10]是由Vapnik等在1995年根据统计学习原理提出的一种新的学习方法。SVM模型可以实现对小样本高维、非线性系统准确拟合，在手写识别、脸部识别、文本分类、回归建模与预测等方面运用较多并取得较好效果。

已知训练集S={(x1，y1)，…，(xl，yl)}(其中，l为样本数量；xi∈Rn；yi∈R；i=1，2，…，l；n为xi向量维数；R为实数集)。对于非线性问题，通过非线性变换将输入向量映射到高维特征空间，转化为线性回归问题。将原训练集S通过映射f=φ(x)变为高维空间Z，则对回归问题就转变为确定一个最优的基于训练集Z的函数：

使得|yi−f(xi)|≤ε成立。式中：i=1，…，l；ε为任意小的数；α为拉格兰日乘子；ω为权重；b为偏置量。S中的点到f(x)的距离di为

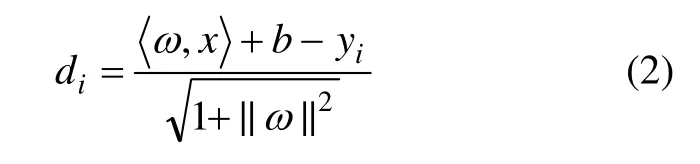
于是，有

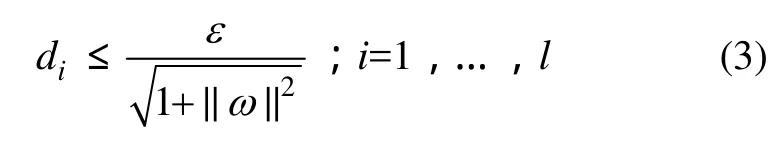
所以，通过最大化di即最小化||ω||2，就可以得到最优f(x)，此时回归问题化为优化问题。考虑到可能误差，引入松弛变量ξi，ξi*≥0(i=1，…，l)，优化方程为

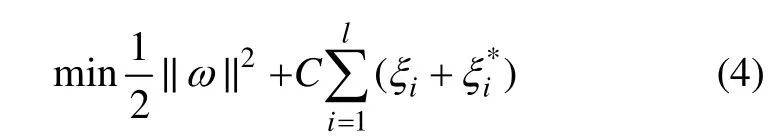
约束为

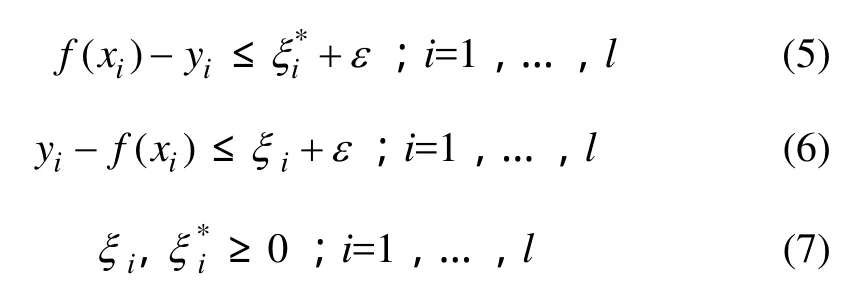
式中：C为惩罚因子。

引入拉格朗日函数：

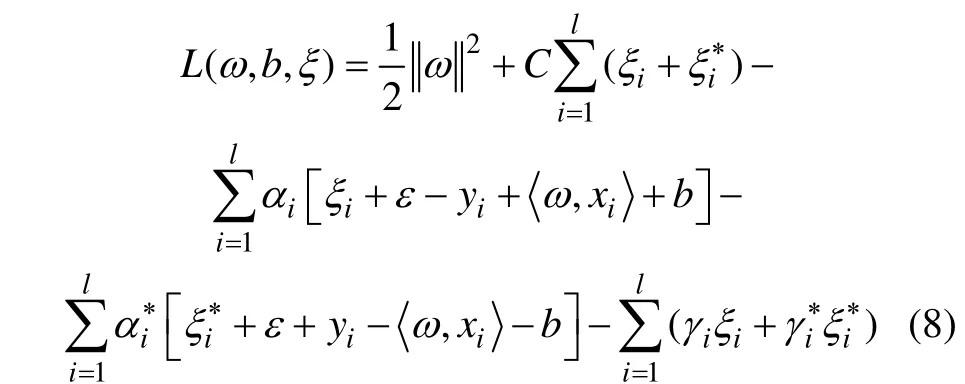
式中：α和γ为拉格朗日乘子。分别对式(8)中ω，ξ和b求偏微分，可得

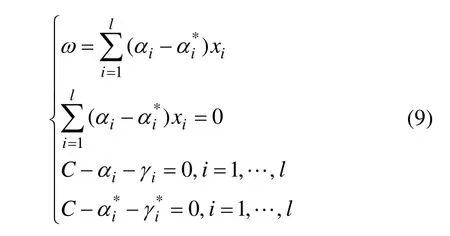
消去ω和γ，求出α，可得f(x)的表达式为

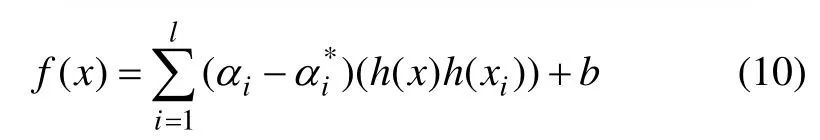
由于仅仅需要计算特征空间中向量之间的内积，故据 Hilbert-Schmidt理论，引入核函数K(x，xi)=h(x)h(xi)[11]，代入式(10)得到f(x)的表达式为

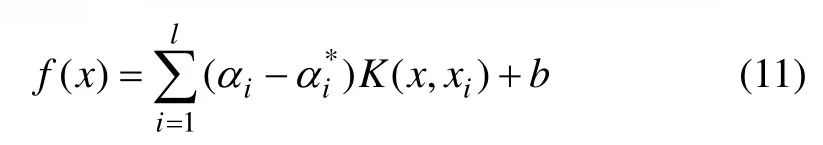
这样就避免了“维数灾难”。目前，常用的核函数有10多种，其中，高斯核函数(RBF)为

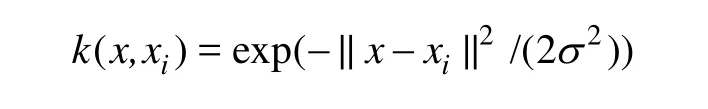
其中：σ为核函数参数。经过验证，能使SVM获得非常平滑的估计。

2 基于GA的SVM预测模型建立

2.1 数据归一化

由于样本中各个指标互不相同，原始样本中各向量的数量级差别很大，为了计算方便，在研究中对样本数据进行归一化处理。利用向量归一化到区间[0，1]之间。归一化公式为

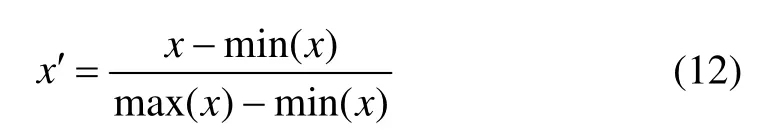
2.2 基于遗传算法的SVM参数寻优

遗传算法(genetic algorithm)[12−13]是一类借鉴生物界的进化规律(适者生存、优胜劣汰遗传机制)演化而来的随机化搜索方法。它是由Holland[14]于1975年首先提出，其主要特点是：直接对结构对象进行操作，不存在求导和函数连续性的限定；具有内在的隐并行性和强大的获得全局最优解能力；遗传寻优方法能获取和指导搜索优化的空间，并能够调整搜索方向，不需要给定规则。

GA具有强大的全局寻优能力[15]，克服了核函数参数的随意选择对其回归模型带来的巨大误差。根据所建立的 SVM 模型，确定以预测值的均方误差作为遗传寻优的适应度函数，适应度越小，则预测值越精确，所寻找到的 SVM 模型参数也就越优，模型也就越好。

Vapnik等在研究中发现核函数的参数σ和惩罚因子C是影响性能的关键因素。因为核函数参数σ影响样本数据在高维特征空间，惩罚因子C则在特征空间中调节 SVM 的置信范周和经验风险的比例[16]，而交叉概率p影响算法的收敛速度及结果的随机性。换言之，SVM模型的性能依赖于参数之间的相互作用，需同时优化全部参数。遗传算法的基本步骤如下。

(1) 编码。采用通用的二进制编码法，以σ，C和p这3个参数的二进制编码随机组合构成n组染色体。

(2) 选择合适的参数。包括群体大小M(一般取20～100)、遗传代数T(一般取 100～500)，依据实际数据复杂程度进行选择。

(3) 确定适应值函数。根据SVM回归预测模型，要想得到精度高的回归函数，必须使预测值与实际值的误差尽量小，使回归曲线与实际曲线贴近，因此，确定把均方误差作为适应值函数。显然，适应值越小，模型越精确。

(4) 随机生成群体。

(5) 进行遗传迭代，直到满足停止条件(遗传代数达到)为止，得到最优SVM参数。

最终得到的GA_SVM结合关系如图1所示。

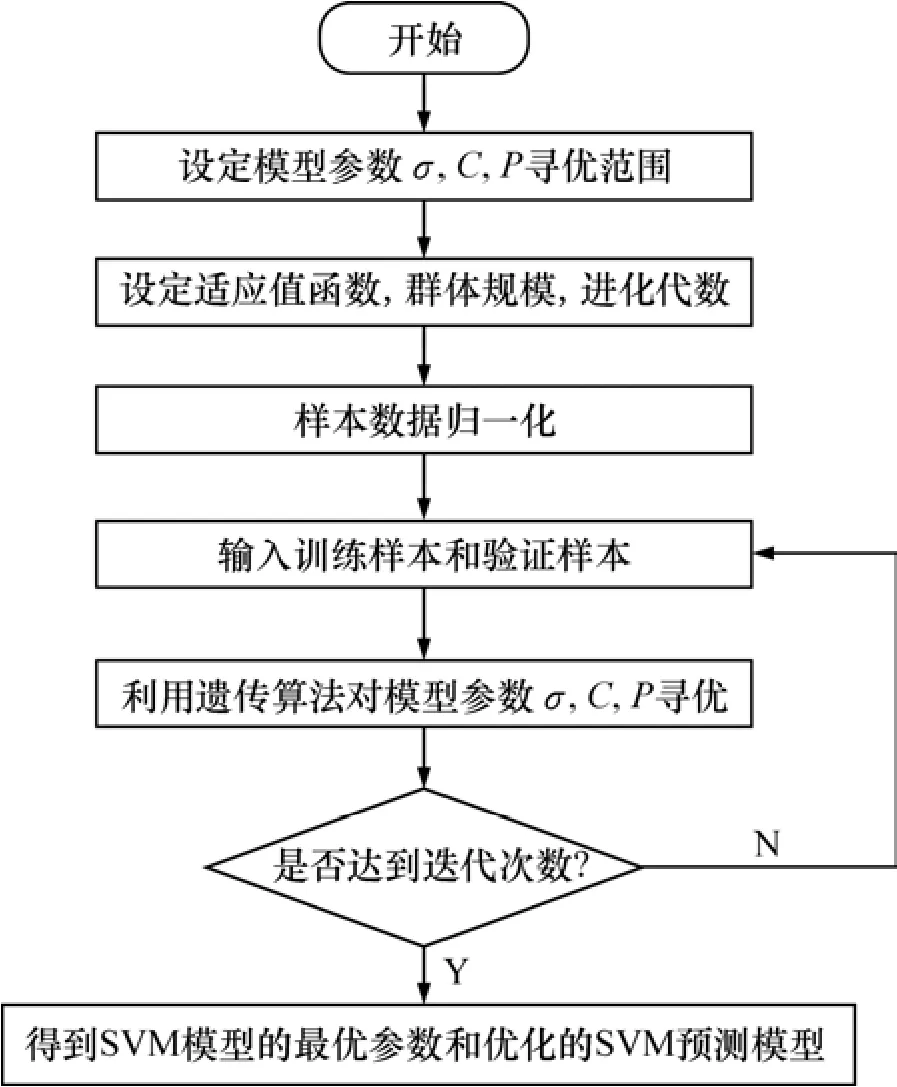
3 工程实例

以某矿为例，运用 GA_SVM 模型对矿山充填钻孔寿命进行预测。由于矿区充填原料及充填配比、围岩条件等基本相同，在建立模型时，为减少分析工作量，提高预测精度，不考虑这些因素，仅分析钻孔直径、钻孔偏斜率以及充填倍线这3个主要影响因素，研究其与钻孔使用寿命(用累计充填量表示)之间的关系。

3.1 数据处理

选取该矿区典型的20个钻孔资料建立样本数据，如表1所示。其中，前10个钻孔作为训练集(用来对SVM 进行训练)，11～15号钻孔作为验证集(用来对SVM模型的核函数的参数进行优选)，最后5个钻孔数据为预测集，对充填钻孔使用寿命进行预测。对样本数据归一化到区间(0,1)，所得结果如表2所示。

3.2 SVM模型确立

将表2中管道内径、偏斜率、充填倍线作为输入因素，累计充填量作为输出因素。根据 SVM 原理，将训练集代入式(10)，求出其中参数，得到确定的SVM模型。

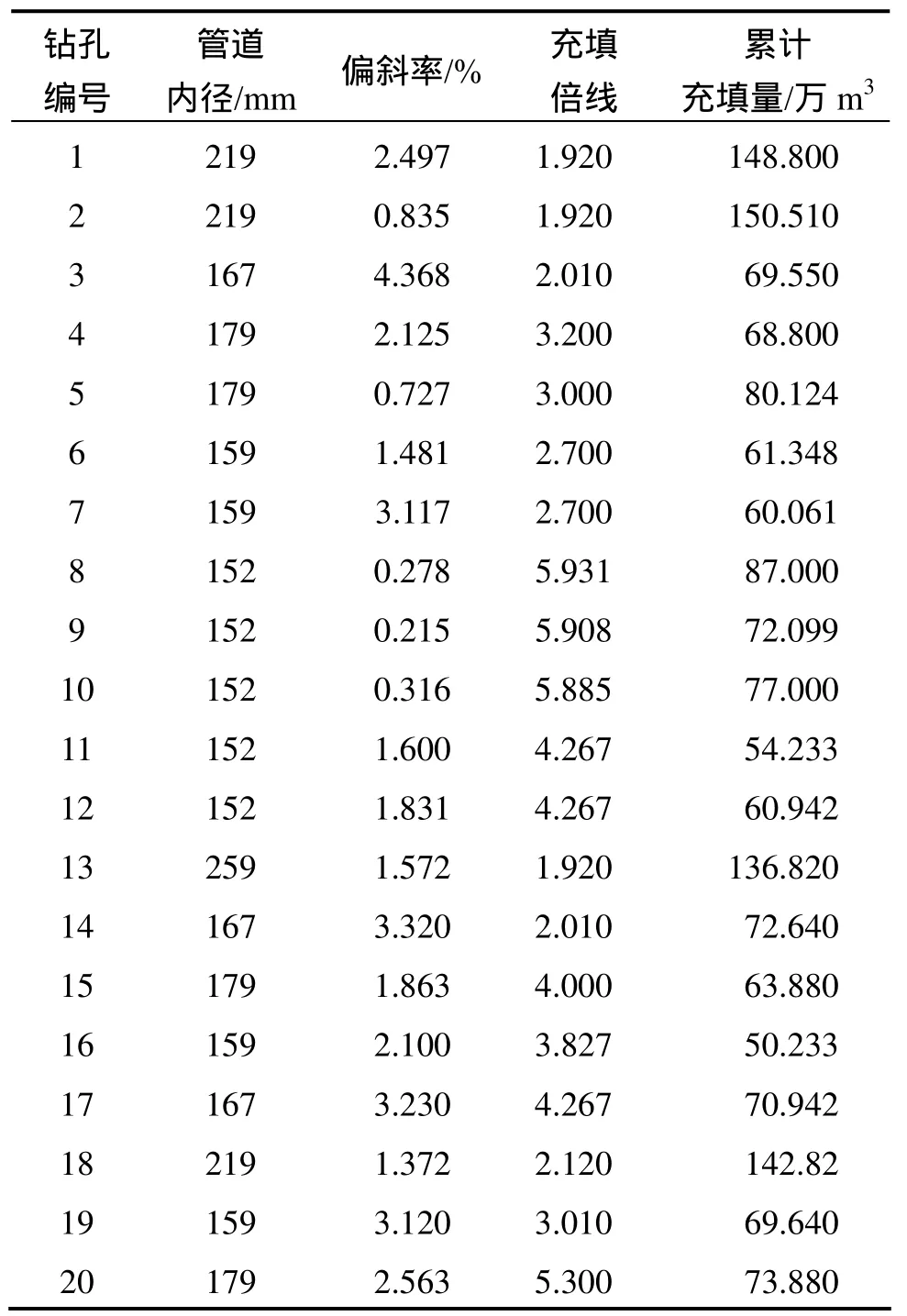
表1 学习样本参数Table 1 Learning sample parameters

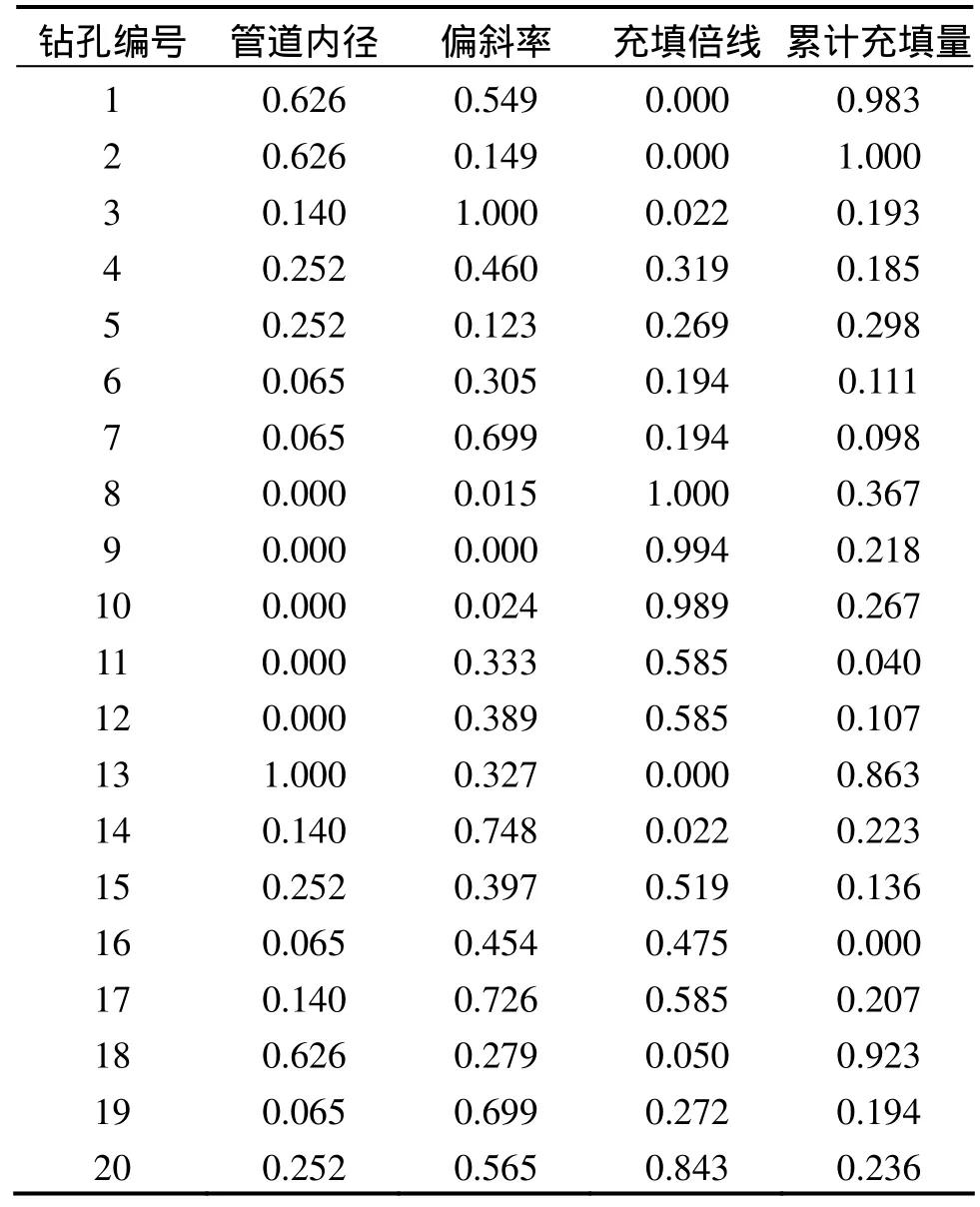
表2 归一化后的无量纲样本参数Table 2 Normalized sample parameters

3.3 GA_SVM模型的确立

由于得到的 SVM 模型中，高斯核函数的参数σ在一般情况下根据经验随即选取，这样，对模型的精确性带来很大的随机误差，为此，运用GA对参数σ优化选择，以验证集的均方误差作为GA的适应度函数。其他参数如下：种群规模为40，进化代数为200，核函数参数σ、惩罚系数C寻优范围为(0，100)，交叉概率p范围为(0,1)。按照图1所示流程，运用matlab计算得到GA_SVM模型最优参数：适应值(均方误差)为0.011 1，惩罚系数C为47.076 8，核函数参数σ为2.263 8，交叉变异概率p为0.045 26。

3.4 优化模型的应用

运用得到的 GA_SVM 模型对预测集进行预测，将预测集的输入因素输入模型，得到的预测结果如图2所示，预测结果如表3所示。

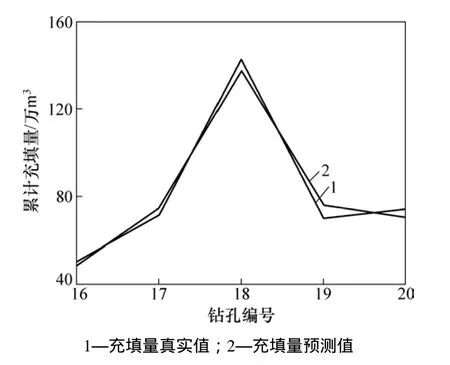
图2 预测结果与实际值曲线Fig. 2 Curve of predicted results and actual results

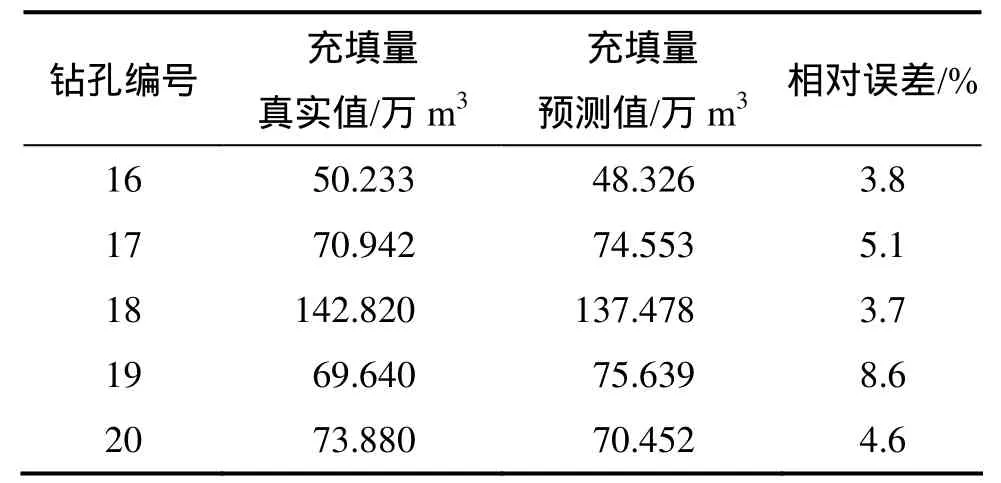
表3 模型预测结果与分析Table 3 Results and analysis of model predictions

从图2和表3可以看出：模型的拟合结果较好，充填量经模型预测所得结果与实际结果误对误差较小，均控制在10%以内，并且大多数相对误差控制在5%左右，模型预测精度较高。

3.5 模型比较

BP神经网络在回归方面运用广泛，为了说明GA_SVM的优越性，将前15组数据作为训练样本，后 5组数据作为测试样本。输入和输出与 GA_SVM模型的一样，利用 3-9-1神经网络结构对充填钻孔寿命进行预测，得到的结果如表4所示。从表4可以看出：由于样本数据少，充填量拟合结果误差波动较大(4.8%～13.6%)。

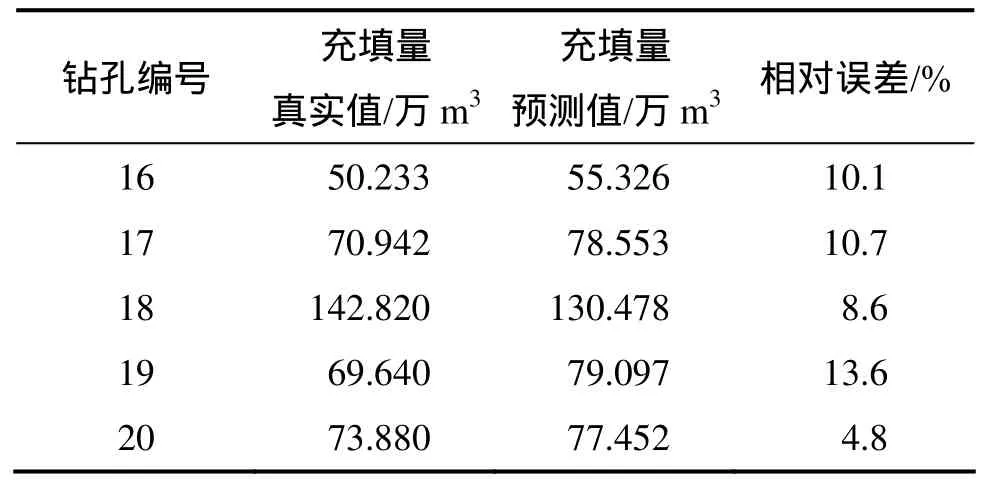
表4 BP神经网络预测值Table 4 Predictive value of BP

2种模型对充填钻孔充填量预测结果分析如表 5所示。从表5可以看出：虽然两者相对误差相差不大，但从平均相对误差和平均绝对误差可知经 GA_SVM模型预测结果更稳定，也更精确。

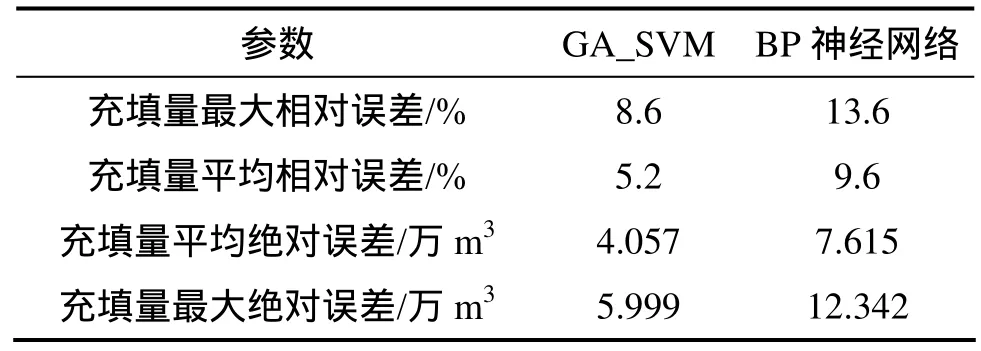
表5 模型钻孔充填量精度分析Table 5 Accuracy of model of drill-hole filling

4 结论

(1) 预测方法的选择是预测模型建立的关键步骤。根据 SVM 原理，建立以管道内径、偏斜率和充填倍线为输入，以充填钻孔寿命(累计充填量)为输出的预测模型。因 SVM 基于小样本统计学习原理和结构风险最小化原则等优点，确保了模型的合理性。

(2) 结合遗传算法，构建GA_SVM模型，经计算得到模型的最优参数(C=47.076 8，σ=2.263 8)和预测结果，预测结果最大相对误差为8.6%，平均相对误差为5.2%。对于环境和影响因素复杂的充填钻孔，精度很高，可以为提前保护和维修钻孔提供依据。

(3) GA_SVM模型与BP模型相比，GA_SVM模型在小样本中能够更好地对数据进行拟合，预测精度更高，在其他类似工程中有较大的推广价值。

[1]王新民, 肖卫国, 张钦礼. 深井矿山充填理论与技术[M]. 长沙: 中南大学出版社, 2005: 1−20.WANG Xinmin, XIAO Weiguo, ZHANG Qinli. The theory and technology of deep mine filling[M]. Changsha: Central South University Press, 2005: 1−20.

[2]周爱民, 古德生. 基于工业生态学的矿山充填模式[J]. 中南大学学报(自然科学版), 2004, 35(3): 468−472.ZHOU Aimin, GU Desheng. Mine-filling model based on industrial ecology[J]. Journal of Central South University(Science and Technology), 2004, 35(3): 468−472.

[3]张德明, 王新民, 郑晶晶, 等. 深井充填钻孔内管道磨损机理及成因分析[J]. 武汉理工大学学报, 2010, 32(13): 100−105.ZHANG Deming, WANG Xinmin, ZHENG Jingjing, et al. Wear mechanism and causes of backfilling drill holes pipelines in deep mine[J]. Journal of Wuhan University of Technology, 2010,32(13): 100−105.

[4]Desai V S, Crook J N, Overstreet G A. A comparison of eural networks and linear scoring models in the credit union environment[J]. European Journal of Operational Research, 1996,18: 15−26.

[5]Piramuthu S. Financial credit risk evaluation with neural and neurofuzzy systems[J]. European Journal of Operational Research, 1999, 112(2): 310−321.

[6]李蒙, 郭鑫, 谭显东, 等. 基于改进 BP神经网络和工业重构理论的用电增长预测方法[J]. 中南大学学报(自然科学版),2007, 38(1): 143−147.LI Meng, GUO Xin, TAN Xiandong, et al. Predictive method for power growth based on improved BP neural network and rebuilding of new industry structure[J]. Journal of Central South University (Science and Technology), 2007, 38(1): 143−147.

[7]郑晶晶, 张钦礼, 王新民. 基于BP 神经网络的充填钻孔使用寿命预测[J]. 湘潭师范学院学报(自然科学版), 2008, 30(4):40−44.ZHENG Jingjing, ZHANG Qinli, WANG Xinmin. Fill drilling service life prediction based on BP neural network[J]. Journal of Xiangtan Normal University (Natural Science Edition), 2008,30(4): 40−44.

[8]王定成, 方廷健, 高理富, 等. 支持向量机回归在线建模及应用[J]. 控制与决策, 2003, 18(1): 89−95.WANG Dingcheng, FANG Tingjian, GAO Lifu, et al. Support vector machine regression on-line modeling and its applications[J]. Control and Decision, 2003, 18(1): 89−95.

[9]李伟超, 宋大猛, 陈斌. 基于遗传算法的人工神经网络[J]. 计算机工程与设计, 2006, 27(2): 316−318.LI Weichao, SONG Dameng, CHENG Bin. Artificial neural network based on genetic algorithm[J]. Compute Engineering and Design, 2006, 27(2): 316−318.

[10]金宝强, 童凯军, 孙红杰, 等. 一种时变耦合模型在油井产量预测中的应用[J]. 科技导报, 2010, 28(17): 72−76.JIN Baoqiang, TONG Kaijun, SUN Hongjie, et al. Application of time varying coupling model in prediction of well production[J].Science ＆ Technology, 2010, 28(17): 72−76.

[11]Jae H M, Y C L. Bankruptcy prediction using support vector machine with optimal choice of kernel function parameters[J].Expert Systems with Application, 2005, 28(4): 603−614.

[12]郑春红, 焦李成, 郑贵文. 基于GA的遥感图像目标SVM自动识别[J]. 控制与决策, 2005, 20(11): 1212−1215.ZHENG Chunhong, JIAO Licheng, ZHENG Guiwen. Genetic algorithm- based SVM for automatic target classification of remote sensing images[J]. Control and Decision, 2005, 20(11):1212−1215.

[13]杨宏辉, 孙进才, 袁骏. 基于支持向量机和遗传算法的水下目标特征选择算法[J]. 西北工业大学学报, 2005, 23(4):512−515.YANG Honghui, SUN Jincai, YUAN Jun. A new met ho d for feature selection for underwater acoustic tar gets[J]. Journal of North Western Polytechnical University, 2005, 23(4): 512−515.

[14]Holland J H. Adaptation in natural and artificial systems[M].Ann Arbor: University of Michigan Press, 1975: 1−20.

[15]李杰, 楚恒, 朱维乐, 等. 基于支持向量机和遗传算法的纹理识别[J]. 四川大学学报, 2005, 37(4): 104−108.LI Jie, CHU Heng, ZHU Weile, et al. Texture recognition using support vector machines and genetic algorithm[J]. Journal of Sichuan University, 2005, 37(4): 104−108.

[16]李蓓智, 李立强, 杨建国, 等. 基于 GA-SVM 的质量预测系统设计和实现[J]. 计算机工程, 2011, 37(1): 167−169.LI Beizhi, LI Liqiang, YANG Jianguo, et al. Design and implementation of quality prediction system based on GA-SVM[J]. Computer Engineering, 2011, 37(1): 167−169.