我的数学应用问题研究之路
余继光

一、18年高中数学应用问题的教学与研究
1995年高考数学命题中引入数学应用题,这一举动影响着全国的基础教育,尤其是高中数学教学. 处在教学第一线的数学教师开始参与数学应用题的编制与教学研究. 下面与同行谈谈我也被卷在其中的经历,以期共同探讨研究.
(一)第一阶段——课堂内外引领学生应用实践,教学之余编制数学应用问题
1995~1999年,由于数学应用问题教学的需要,在数学教育专家引领下,数学应用问题编制与研究开始在全国各地兴起. 许多中学数学杂志在此领域大量发表文章,尤其是《数学通讯》杂志集中报道数学应用方面的研究成果. 但是,在中学数学第一线,教师的数学应用意识与应用问题教学意识都不强,教师数学应用问题的知识储备也不足,再加上学生的社会实践知识欠缺,阅读理解力的薄弱,面对高考数学应用题时,学生的应试心理一般处于恐惧或放弃状态.
1.编制适合中学生的数学应用问题,研究中学数学建模问题
此时我开始潜心思考,从现实生活中寻找信息与资料,编制具有活生生现实背景的数学应用题,并发表在《数学通讯》等杂志上,还将编写的数学应用题分类汇集,编著《用数学眼光看世界》一书. 如下面例题,在当时起到较好的引导作用.
例1 为了提供更加优质的教育,增加大学生就业岗位,某地区准备逐步实现小班化教育,将学生人均教室面积由1 m2提升至x(m2),x≤2,调整教师人均办公室面积为
y=f(x)=4, 1≤x<1.5,
ax+b,1.5≤x≤2.
如图1,
①确定a,b的值及函数f(x)值域;
②实行小班化,对教室改造投资中,投资额P(万元)与x之间的关系是P=exf(x),探求教室改造投资的最大值;
③对办公室进行改造的投资中,投资额Q(万元)与y之间的关系是Q=5y3-3cy2+180,c为正常数,探求办公室改造投资的最小值及相应c的范围.
2.利用周末时间带领学生开始数学应用实践和实习活动,增强学生应用意识
数学应用意识的培养不仅可以通过数学应用问题的教学,还突出地表现在数学应用实践中. 在周末组织学生开展数学应用实践活动,如利用简易工具测量鉴湖明珠电视塔高度以及与观测点距离问题. 学生不仅创造性实践(多种测量方式),而且撰写了2000字左右的实习报告,将实习过程、测量方法、测量所使用的数学原理、测量后所建立的数学模型,一一总结记录,并写下自己的实践感想.
(二)第二阶段——数学教学加大数学应用问题教学力度,探究数学应用题的教育功能
进入新世纪,新的课程改革措施出台,在以培养中学生的创新意识和实践能力为总目标形势下,中学的数学应用问题教学有所加强. 高考数学试卷中的数学应用题分值不断增大,数学应用题命题更加贴近学生的生活实际和认知水平. 学生面对数学应用题时开始充满自信,各地高考数学应用题的成绩不断提高. 在这一阶段全国的中学数学杂志上有关数学应用的文章层出不穷,为各地中学教师开展数学应用问题教学提供素材.
1.数学应用问题的教育功能开发
数学应用问题教学的目的是提升中学生的数学应用意识,培养中学生的数学应用实践能力.开发数学应用的教育功能除了它对数学思想方法的深入理解外,让学生通过一个个“活”的数学应用问题,体会问题背后所隐含的环境保护、再生资源利用、爱心感恩、资源利用最优化等.
2.开设数学应用问题讲座,普及中学数学建模方法
为了普及中学数学建模思想方法,除了课堂上的数学应用问题教学之外,利用课外活动或研究性学习活动时间开设数学应用问题讲座,使数学应用教学形成一个完整的体系,给中学生一个数学应用问题全貌.
3.挖掘课堂教学案例,提升中学生的实践能力与创新意识
在数学教学过程中,常常会遇到一些不可多得的智慧火花,开发它,会引发无限的创造力.
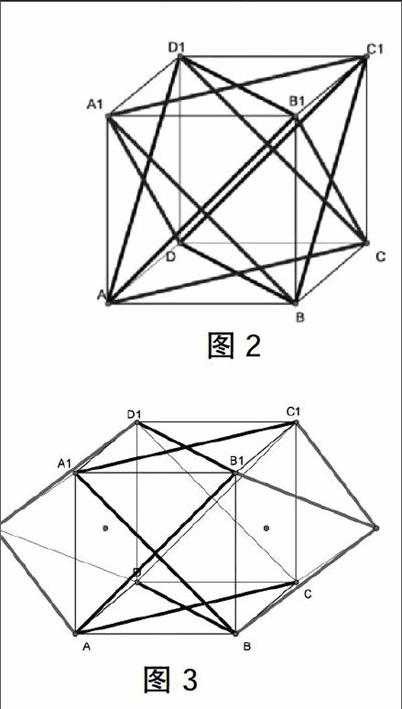
例2 利用正方体框图,请你构造一个面数大于6的多面体.画出你设计的多面体的直观图,数一数它们有多少棱、多少个面、多少个顶点.
这个开放性作业布置后的第二天上课时,有一位同学拿着一个正方体铁丝骨架模型,如图2,其中六条面对角线是用橡皮筋连接的,一位同学将一对面对角线橡皮筋向外拉,然后问其他同学,这是不是一个多面体?如图3,一位同学说这个多面体形成一个12面体. 接着,另一位同学伸出手将另一对面对角线橡皮筋向外拉,“认为”形成一个18面体.第三位同学将最后一对面对角线橡皮筋向外拉,“认为”形成一个24面体.在四位同学的共同合作下,一个生动的多面体诞生了.面对课堂教学中瞬间发生的信息,教师用敏锐的眼光发现其中的问题并加以开发,不仅与欧拉公式发生联系,而且总结其中的数学模型.
(三)第三阶段——开发数学应用题的数学本质与数学应用意识
2003年新课程改革起步,新课程标准制定并公布,2004年在广东、海南、山东、宁夏新课程教材进入高中课堂,各地编写的新课程教材纷纷出版,新课程数学教材中最明显的特点就是数学应用问题比原教材增加了许多,高考中许多数学应用题的情境来自于生活,深入挖掘出其数学本质,最有代表性的就是处在二期课改前线的上海,开发的数学应用题给人们呈现出的情境新颖,其数学内涵丰富.
1.关注数学应用建模能力,培养学生数学应用素质
中学所涉及的数学应用问题有二类:第一类,经过精加工后的贴近数学本质的“准”数学应用题;第二类,经过粗加工的贴近实际的“真”数学应用题. “好”的数学应用问题层出不穷,面对如此好的问题.把数学应用建模思想方法渗透在教学之中,充分挖掘问题的数学本质,把这一过程成为养育中学生数学应用素质的重要途径.
例3 以下是面点师一个工作环节的数学模型:如图4,在数轴上截取与闭区间[0,1]对应的线段,对折后(坐标1所对应的点与原点重合)再均匀地拉成1个单位长度的线段,这一过程称为一次操作(例如在第一次操作完成后,原来的坐标,变成,原来的坐标变成1等).那么原闭区间[0,1]上(除两个端点外)的点,在第二次操作完成后,恰好被拉到与 1重合的点所对应的坐标是 ;原闭区间[0,1]上(除两个端点外)的点,在第n次操作完成后(n≥1),恰好被拉到与1重合的点所对应的坐标为 .
理解突破:
“均匀地拉”——保证这是一个有规律的数学变换——伸缩变换;
“一次操作”—— 一次变换所呈现的结果:原来的变到1;原来的,变到;
第2次操作——第1次操作后由原来的,,变到第2次操作前的;第2次操作后的1;
第3次操作——第1次操作后由原来的,,,变到第2次操作前的,,第2次操作后变到;第3次操作后变到1;照此下去,……;
第n次操作——第1次操作后由原来的,,…,,变到第2次操作前的,…,,第2次操作后变到,…,;…,第n-1次操作前的,,第n-1操作后的;第n次操作后变到1;
因此第二次操作完成后,恰好被拉到与 1重合的点所对应的坐标是,;原闭区间[0,1]上(除两个端点外)的点,在第n次操作完成后(n≥1),恰好被拉到与1重合的点所对应的坐标为,,…,,,即,j为[1,2n]中的所有奇数.
看到此问题情境,不由联想起古人“一尺之棰,日取其半,万世不竭”的精美概括;联想到精美的杨辉三角,那么此问题能否概括为“一尺之面,对折其拉,万丝不断”?生活中的“拉面”场景,抽象为一种数学伸缩变换过程,检测学生的对应、变换、数列知识以及逻辑思维能力,此问题给我们的一个重要启示是:在数学教学中,引导学生学会用数学眼光看世界,去发现生活中的司空见惯的现象背后的数学规律,去探索或总结其数学模型,去揭示实际应用问题的数学本质.
2.关注数学问题的数学本质,从实际问题中挖掘数学模型
例4 如图5,一位花布设计师在边长为3的正方形ABCD中设计图案,他分别以A,B,C,D为圆心,以b(0≤b≤3)为半径画圆,由正方形内的圆弧与正方形边上的线段构成了丰富多彩的图形,则这些图形中实线部分总长度的最大值为 ,最小值为 .
理解突破:L=2bπ+4(3-2b), 0
≤,
2bπ+4(2b-3),
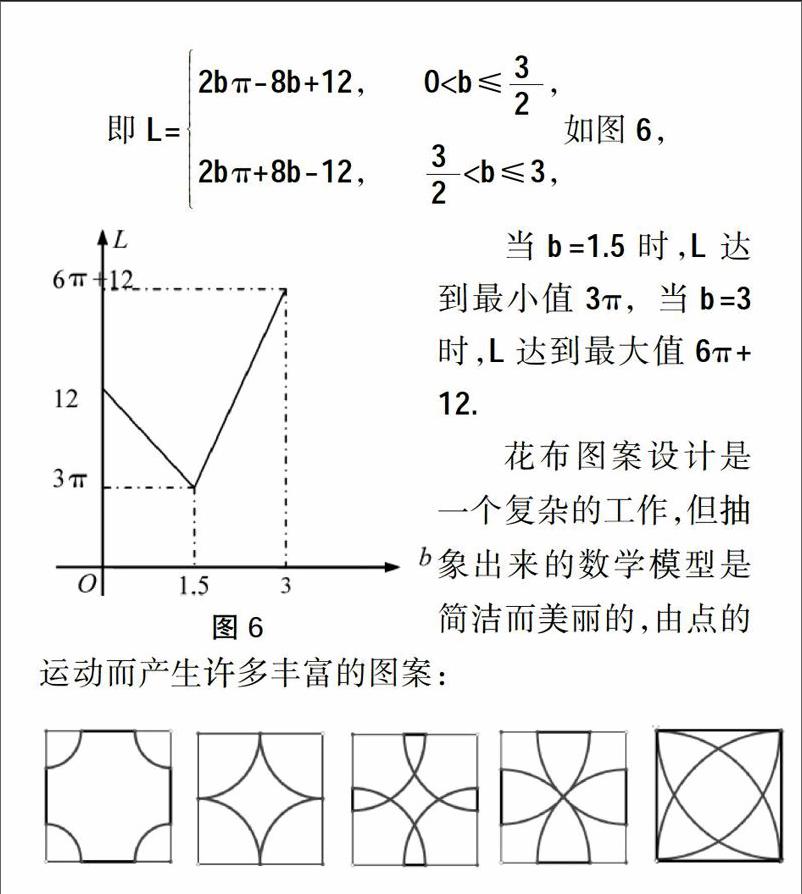
即L=2bπ-8b+12, 0 ≤, 2bπ+8b-12, 当b=1.5时,L达到最小值3π,当b=3时,L达到最大值6π+12. 花布图案设计是一个复杂的工作,但抽象出来的数学模型是简洁而美丽的,由点的运动而产生许多丰富的图案: 学生面对如此问题时,一方面要学会从“数”角度思考,写出长度的分段函数,而后求出其最大值与最小值;另一方面也应学会从“形”角度思考,发现其最值点和最值. 但不论是哪一个思路,都需要学生在“运动”着的图案中发现其数学本质,为今后的创新意识和实践能力打下基础,这正是新课程改革的教育理念之一. 二、近20年来我国高中数学应用问题教学的反思 近20年来高中数学应用问题教学重视程度不同,特别在高考单独命题省份. 数学应用题一般都有一大一小或一大二小. 尤其是上海进行二期课改,关注数学研究性学习,数学应用问题教学的氛围比较浓. 高考数学命题中数学应用题情境新颖、充分挖掘实际问题中的数学本质. 但是许多省份的单独命题中,除了概率统计的应用题外,几乎不涉及数学应用问题. (一)数学教学中实际应用意识不强,对数学应用问题的教学目标不明确 不论是数学课程标准还是考试要求对应用意识都有明确的说明:“能综合应用所学数学知识、思想和方法解决问题,包括解决在相关学科、生产、生活中简单的数学问题,能理解对问题陈述的材料,并对所提供的信息资料进行归纳、整理和分类,将实际问题抽象为数学问题,应用相关的数学方法解决问题并加以验证,并能用数学语言正确地表达和说明,主要过程是依据现实的生活背景,提炼相关的数量关系,将现实问题转化为数学问题,构造数学模型,并加以解决.”实事求是地说,这一目标要求是比较高的.它至少包括了下列目标: 一是“用”数学的意识与能力,即通过教学培养学生数学应用意识,学会用数学眼光看世界的方法,求解数学应用题的能力,探究数学概念与方法的来龙去脉与实际背景的能力; 二是数学建模能力,为相关学科中涉及数学建模或进一步学习中涉及数学建模奠定基础; 三是数学语言表达与交流能力,即通过数学研究性学习方式来培养这一能力; 四是数据处理能力,在学习概率、统计、算法、金融数学相关知识中所训练的能力. (二)数学教学中的功利意识太强,对数学应用问题教学冷热不均,反复无常 1995年以来,数学应用问题教学意识经历了一个由冷加热,热中保温,温度下降的过程. 教师在不同教学思潮的影响下,缺乏从整体上认识它的功能与素质教育要求. 因此一会儿重视,一会儿放弃,表现在对数学教材处理上,有关“实习作业”“章引言与章头图”“探究与发现”“阅读思考”等内容都忽略不去涉及,截头去尾只讲一些与“高考应试”有关的数学内容.课堂上对数学概念的来龙去脉不加研究,不介绍,导致学生只能了解一些数学解题方法,不理解数学概念.由于社会文化中功利意识的影响,在数学教学时对应用问题的教学中,如果与高考数学应用题型相关,就花大量时间或精力去训练学生的应试能力;如果与高考数学应用题型无关,就一带而过,或者是避而不讲.这样导致中学生数学应用意识与实践能力仍是一个盲点. (三)新的课程改革促使数学应用再掀高潮 2012年起,浙江省在全省范围内进行大规模的课程改革,增大选修课程的学分,以数学建模为核心的数学应用教学研究在浙江大地展开,2014年浙江高考数学中,一道闪亮的应用题诞生,可以预见数学应用问题的教与学会再掀高潮! 例5 某人在垂直于水平地面ABC的墙面前的A点处进行射击训练. 已知点A到墙面的距离为AB,某目标点P沿墙面的射线CM移动,此人为了准确瞄准目标点P,需计算由点A观察点P的仰角θ的大小.若AB=15m,AC=25m,∠BCM=30°, 则tanθ的最大值 .(仰角θ为直线AP与平面ABC所成角) 审题:为求一个直线与平面所成角,第一步找射影,于是过P作PP1⊥BC交BC于P1,连结AP1;第二步,计算比值,问题的关键是AP1,PP1与谁有关系?第三步,找自变量BP1=x,因为AP1,PP1都随着P的运动而变,导致P的射影P1在动,而此时沟通它们之间的关键量是BP1,经过这三步就可以建立起数学模型.

