基于K-modes聚类的半导体封装测试粗日投料控制

姚丽丽，史海波，刘 昶

（1.中国科学院 沈阳自动化研究所，辽宁 沈阳 110016；2.中国科学院大学，北京 100049）

0 引言

半导体封装测试制造系统的调度问题一般分为投料控制、派工调度和重调度三方面，其中，投料控制是半导体封装测试制造系统调度的重要组成部分，位于半导体封装测试调度体系的最前端，在整个半导体封装测试制造过程中占据重要地位。投料控制策略对制造系统性能的影响很大［1］，早在1988年Wein［2］就指出，投料策略比派工策略对半导体前道晶圆制造系统的影响更大。同样，对于多品种混合投产的后道封装测试来说，投料策略的优劣对制造系统性能的影响也具有至关重要的作用。

投料策略需要解决投入什么料、投入多少量和何时投的问题。在半导体封装测试中，投料控制主要包括周投料控制和日投料控制两个层级。周投料控制确定本周期内生产的品种和每个品种所需的生产产量，属于计划层研究问题，主要根据订单承诺信息和产能规划信息实现周期生产产品分配；日投料控制根据周投料计划，确定每日的投料品种、投入品种的数量和每一品种的具体投放时刻。日投料控制又包括粗日投料控制和细日投料控制［3］，其中，粗日投料控制主要根据周计划确定每日投料品种和每个品种的投入数量；细日投料控制则根据粗日投料计划确定各个投产品种的具体投放时刻。近年来，各个制造领域的投料控制研究主要集中在细日投料控制问题，即主要对确定投料时刻问题进行研究，并提出了多种投料策略，如固定时间投料策略［4］、恒定在制品投料策略［5］、避免饥饿（Starvation Avoidance，SA）投料策略［6］等。半导体封装测试投料控制的研究也主要集中在细日投料控制方面，如Liu等［6］提出一种新的多规则嵌入的投料控制策略，综合考虑Lot优先规则、产能分配规则和机器加载规则，对投料品种的顺序和工作中心分配进行确定，它实际上是一种投料派工结合的控制策略；Ryohei等［7］提出一种基于遗传算法和机器学习结果的投料控制方法，利用遗传算法产生合适的规则，对产品的具体投料时刻进行确定；Chua［8］等基于多约束有限能力的智能投料控制系统，首先对投入品种依据品种属性信息进行排序，然后依据产能情况对该顺序进行调整，最后进行设备指派。粗日投料策略以往多被认为是生产线上的投料员所关注，不作为学术研究的重点［1］，目前还未看到半导体封装测试粗日投料控制方面的研究文献。然而，对于半导体封装测试生产来说，多品种混线生产和产能限定约束多是其显著特点，粗日投料控制确定的日投料品种影响着细日投料控制以后续派工调度，因此研究半导体封装测试的粗日投料控制，对于提高半导体制造系统的整体性能有重要的意义。

半导体封装测试是典型的基于订单驱动（Make to Order，MTO）型企业，生产的品种繁多，如某封装测试企业生产的品种约4万种。虽然封装测试企业的设备规模也很庞大，如某工序有上千台设备，但是依然达不到生产品种与设备的固定对应，一台机器上往往对应多个生产品种的更换加工。当更换不同加工条件的品种时，往往伴随着设备上加工材料或工夹具等的更换，这些更换常常产生一定的时间成本代价，生产车间称为改机现象。例如封装测试中的塑封工序，同一台设备上前后连续两个加工品种所用的模具不同，其更换模具需要约4h 左右。改机现象的存在导致封装测试企业设备利用率偏低，生产周期较长。如何减少改机代价、提高生产效益，是封装测试企业决策者最为关注的问题。本文以某半导体封装测试企业为研究背景，根据企业需求，以降低改机代价为目标，针对半导体封装测试的粗日投料控制问题进行研究，提出一种新的基于Kmodes聚类的综合投料控制策略。该策略以周计划投产品种为输入，采用一种新的量限定属性赋权Kmodes聚类方法，以瓶颈工序产能类型个数作为聚类类别数，依据生产过程中影响改机代价的品种属性信息进行聚类，聚类过程中，对各个类别中的聚类点的数目进行限定。依据聚类结果，采用基于品种平均和投产量平均的综合策略，确定每日投产的品种和每个品种的数量。

2 K-modes聚类方法介绍

本文首次将聚类的思想引入封装测试投料控制中，提出一种新的改进量限定属性赋权K-modes聚类方法，对周计划投产品种进行聚类，在聚类的基础上进行投料控制策略的研究。

2.1 传统K-modes聚类方法介绍

K-modes算法是K-means［9-10］算法的扩展，于1998年由Huang［11］提出，该算法克服了K-means算法仅能处理数值型数据的局限性，采用差异测度来代替K-means算法中的欧式距离，能够很好地对数值属性数据进行聚类。主要处理流程如下：①随机地选择k个对象，每个对象初始代表一个簇的类中心；②对剩余的每个对象，根据与各个簇中心的差异测度进行聚类，将其赋给最近的类簇；③重新确定每个簇的类中心，根据新的类中心进行聚类。该过程不断反复，直到准则函数收敛。

K-modes聚类算法可具体描述如下：

设X=｛x1，x2，x3，…，xn｝为n个对象构成的非空有限集合，A=｛a1，a2，a3，…，am｝为由m 个字符型属性构成的非空有限集合，xi的属性aj可描述为xi=｛xi，1，xi，2，xi，3，…，xi，m｝，数据矩阵具体可表示为式（1），属性aj的值域为DOM（aj）=

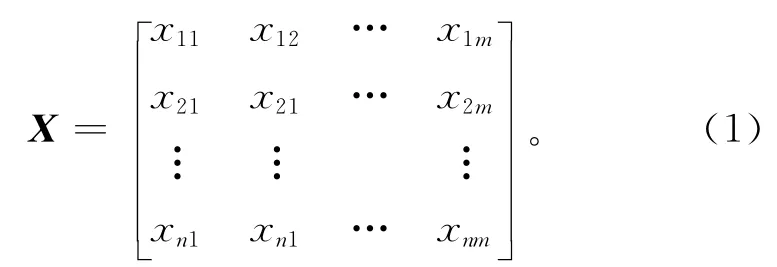
具有分类属性的对象，其差异测度定义为

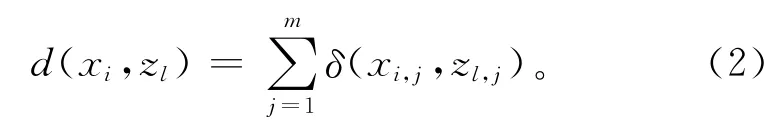
式中：d（xi，zl）为对象xi与类中心zl之间的差异测度，δ（xi，j，zl，j）为0-1变量，如式（3）所示：

通过上两式可以看出，差异测度值d（xi，zl）越小，对象xi与类中心zl之间的相似度越高。当d（xi，zl）=0时，表示对象xi与类中心zl完全相同。聚类过程中，计算对象xi与每个类中心的差异测度值，将xi划分给差异测度值最小的那个类簇。

聚类准则函数是K-modes算法终止的有效判定条件，常采用误差平方和方法作为其准则函数，如式（4）所示：

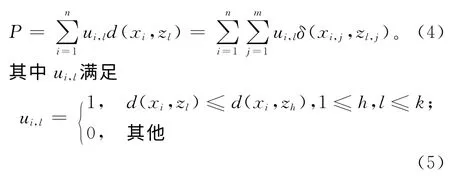
当K-modes进行完一代聚类后，如果准则函数还未收敛，则需要重新确定类簇中心，重新根据新的类簇中心进行聚类。K-modes聚类中心的更新机制定义如下：当且仅当2，3，…，m，目标值（4）取得最小，其中满足

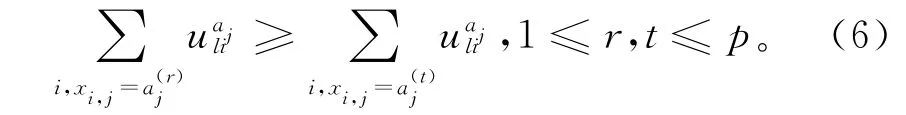
2.2 基于属性加权的K-modes聚类方法介绍

传统的K-modes聚类将所有属性等同处理，故对聚类结果的贡献相同。考虑不同属性对聚类分析结果的不同贡献，需要对各个属性影响程度进行加权处理［12］。假设每个属性的权值为ω1，ω2，…，ωm，ωj≥0，j=1，2，…，m，则加权后的数据对象

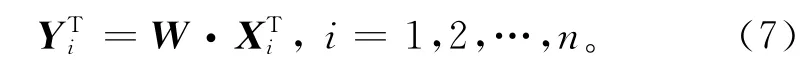
式中W 为权值矩阵，

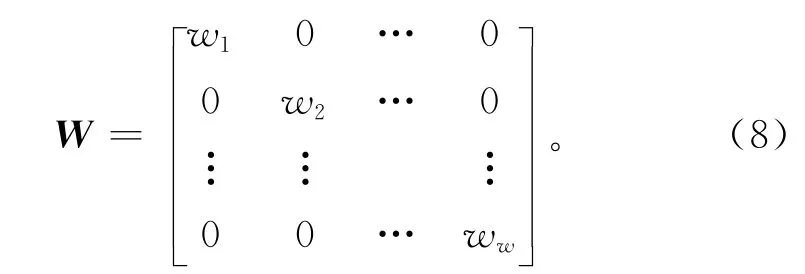
则基于属性加权的K-modes中，两个对象之间的差异测度

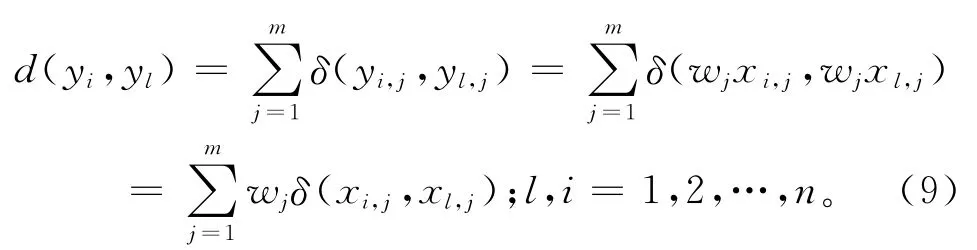
基于属性加权的K-modes的误差平方和聚类准则函数由式（4）变为

基于加权的K-modes聚类中心的更新机制与传统的更新机制一样，可依据式（6）进行更新。

2.3 一种新的量限定属性赋权K-modes聚类方法

基于属性赋权K-modes的聚类方法，各个对象的属性都是文本属性，存在无量属性。考虑对象属性中包含有量属性的情况，本文对基于属性赋权Kmodes的聚类方法进行改进，提出一种新的量限定属性赋权K-modes聚类方法。该方法根据聚类过程中的量属性，对各个类簇所包含的对象数目进行限定。

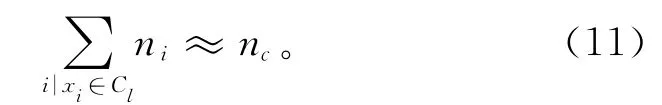
式中：ni表示对象xi的量属性值，Cl表示聚类簇l。

聚类过程中，首先计算差异测度值，并从小到大对各个簇进行排序；然后选择第l（初始l=1）个簇，计算每个簇中已分配点的投产量总合（包括聚类中心点的投产量），如果，则将该点归为簇；否则l=l+1，继续进行检测。

3 基于K-modes聚类的粗日投料控制研究

粗日投料控制的主要任务是根据周计划投产品种和数量信息确定日投产品种和数量。企业中常用的粗日投料策略主要有两种，即基于投产品种平均分配的投料策略和基于品种投产量平均分配的投料策略。基于投产品种平均分配的投料策略，对周计划以品种为单位进行拆分，确定日投产品种；基于投料量平均分配的投料策略，将周计划中各个品种的投产数量平均分配到每日。这两种方法都未考虑品种更换对生产的影响，导致实际生产的改机代价较大。本文提出一种新的基于聚类的投料控制策略，以降低改机代价为目标，首先对周计划投产品种进行聚类分析，在此基础上采用基于品种平均和投产量平均的综合策略，确定每日投产品种和各个品种的投产数量。

3.1 基于量限定属性赋权的K-modes的封装测试投产品种聚类

在聚类方法研究的基础上，进行封装测试投产品种聚类的应用研究。首先进行相关参数的提取与确定。

3.1.1 聚类因素提取与确定

（1）聚类属性及权重确定 半导体封装测试生产中的改机影响因素有圆片尺寸、装片胶、框架型号、模具和塑封料等。不同属性影响品种更换的代价不同，例如模具更换需要约4h，而塑封料更换仅需要15min左右，利用赋权方式对各个属性的改机代价影响程度进行给定，假设单位改机时间代价为t，各个因素的权重因子为ω1，则各因素的改机代价为

（2）聚类类别个数k 的确定 生产过程中的瓶颈环节限制着整个流程的产出速率，同样，其产能的配备情况决定了整个生产品种的分布。投料控制时，应以瓶颈工序的产能类型个数作为聚类类别个数k。在半导体封装测试中，塑封机的价格相对比较昂贵且专用性较强，一台塑封机约几十万美元，企业配备塑封工序的产能较低，导致该工序经常出现瓶颈。因此，在半导体封装测试投料控制时，以塑封工序的产能类型个数作为聚类类别数k。

（3）投产量对聚类结果的影响 一般来说，车间中各个类型的产能基本均衡。本文假设瓶颈工序各个类型的产能均衡，考虑品种投产量对品种划分的影响，对每一类别内的品种投产量总和进行限定，以保证聚类后各个类别的投产量也基本均衡，则每个类别中的总产量约为

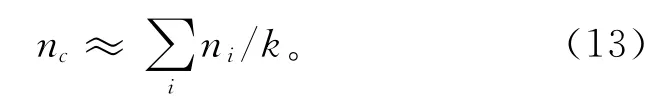
式中：ni表示品种i 的投产量，nc表示类别c 的总产量。

3.1.2 聚类方法应用步骤

本文提出的量限定属性赋权K-modes方法，在半导体封装测试投产品种聚类中的主要应用流程如下：

步骤1 依据封装测试生产过程中瓶颈工序的产能类型个数，确定将要聚类的类别个数k。

步骤2 依据属性对于改机代价的贡献程度，给定改机属性因素的权重ω1，ω2，…，ωm。

步骤4 依据式（9）分别计算剩余的点xi与这k 个聚类中心zl的差异测度值，同时对差异测度值从小到大排序。

步骤5 根据差异测度值选择第l=1个簇，计算每个簇中已分配点的投产量总和（包括聚类中心点的投产量），如果，则将该点归为簇；否则l=l+1。继续比较计算，直到所有点分配完毕。

步骤7 令迭代次数t=1。

步骤8 依据式（6）更新聚类中心，确定k 个新的聚类中心

步骤9 计算每个对象xi到新的聚类中心的差异测度值，同时对差异测度值从小到大排序。

步骤10 根据差异测度值选择第l=1个簇，计算每个簇中已分配点的投产量总和（包括聚类中心点的投产量），如果，则将该点归为簇；否则l=l+1。继续比较计算，直到所有点分配完毕。

3.2 一种新的基于属性赋权K-modes聚类的综合投料控制策略

针对半导体封装测试粗日投料控制，本文提出一种新的基于属性赋权K-modes聚类的综合投料控制策略。该方法在聚类的基础上，提出采用基于品种平均和投产量平均的综合策略，确定每日投产品种和各个品种的投产数量。整个类别采用基于投产量平均的策略，针对类别内各个品种采用基于品种平均的策略。起始投产日期为Rs，投产周期为7 d，该策略主要包括以下步骤：

步骤1 根据周计划投产总量计算每日平均投产量nd，

步骤2 初始化所有类别的品种到待投料集，各个品种包含品种名称、投产量、交货期和所属类别四个字段信息。

步骤3 根据交货期的紧急程度对聚类后各个类别的投产品种分别进行排序，交货期越早，排序越靠前。

步骤4 初始化当前投产日Rd为投产周期的第一天，即Rd=Rs。

步骤5 令投产类别c=1。

步骤6 从待投料集的类别c中，依据先后顺序选择第一个品种ic，如果品种ic的投产量则将该品种全部安排该Rd日进行投产，从待投料集类别c中删除品种ic；否则将品种量在Rd日投产，修改待投料集中ic的投产量为。

步骤7 判断c＞k 是否成立，如果成立，则继续步骤8；否则c=c+1，返回步骤6。

步骤8 判断Rd＞Rs+7是否成立，如果成立则结束，否则Rd=Rd+1，返回步骤5。

4 应用研究

为了说明本文提出的基于K-modes聚类的投料控制策略的应用，下面以7个投产品种、5个影响改机属性的简单模型进行应用过程研究。

4.1 投产品种聚类应用研究

表1所示为周投产计划中的投产品种信息，其中包括品种的投产量、交货日期和相关改机代价影响属性因素；表2所示为影响改机代价的品种属性影响权重。

表1 投产品种信息

表2 改机属性赋权

基于K-modes的品种聚类的主要过程如下：

（1）计算聚类后每个类别中的投产产量

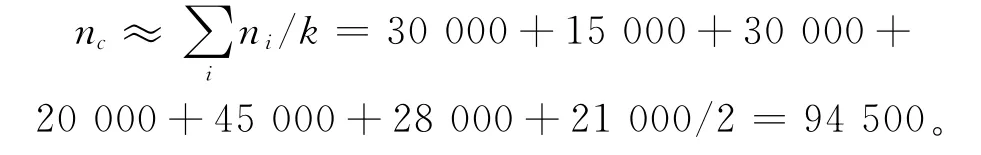
（2）假设随机选择的两个初始聚类中心分别为MC20976P-2和LS028212M，分别计算剩余各个点与这两个中心的差异测度，利用算法步骤中的步骤5进行归类。计算后的差异测度值和类别结果如表3所示。

表3 聚类结果

聚类后，与类中心MC20976P-2的同类别品种分别有MC20976P-1，MC20976P-3，D396650-e3；与类中心LS028212M 同类别的品种有TDA6782M-1和TDA6782M-2。

（3）计算聚类准则函数

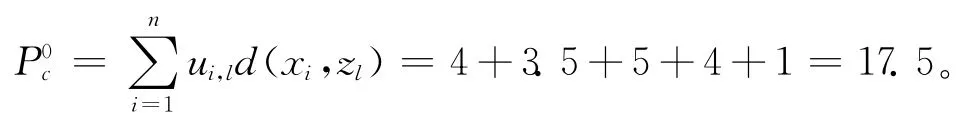
（4）利用聚类中心的更新机制更新聚类中心，更新结果如下：为｛8，UN-6888-I，SDIP32A，TA7698，EME6300H｝，为｛12，UN-6885，JH-100630，T0263E，7300HX｝。

（5）计算所有点与聚类中心的差异测度值，进行类别重新给定，结果与表3相同。

输出聚类结果：类别1 为 MC20976P-1，MC20976P-2，MC20976P-3，D396650-e3；类别2 为TDA6782M-1，TDA6782M-2，LS028212M。

4.2 综合投料策略应用研究

依据聚类结果，假设起始投料日期为18／03／2013，依据本文提出的基于聚类的投料控制策略步骤，得出日投料计划如表4所示。

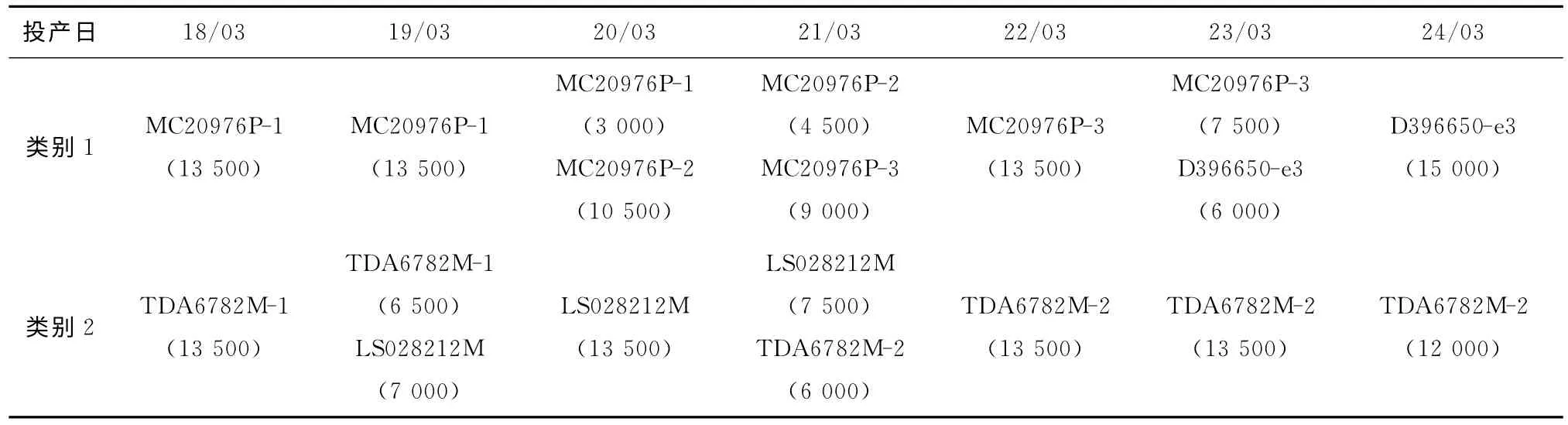
表4 基于聚类的投料控制结果

为了方便得知粗日投料控制策略对生产的影响，假设生产车间只有一道工序，每种类型的产能各有一台机器，改机单位时间为10 min，对本文提出的基于品种聚类的综合投料策略控制下的生产过程进行推演仿真，得到改机频率为5次，改机时间代价为175min。

4.3 实验与比较

为了进一步说明本文提出的基于品种聚类的综合投料控制策略的有效性，对周计划品种个数分别为10和15的规模、瓶颈产能类型个数分别为3和5的数据进行仿真试验，周计划数据如表5 和表6所示。同时，为了进一步说明该策略的优越性，将该策略与常规的基于品种平均分配的策略、基于投产量平均分配的策略和基于遗传算法（Genetic Algorithm，GA）的智能投料控制策略进行比较。基于GA 的智能投料控制策略主要对投料顺序进行优化，其设计思想如下：每个品种代表一个基因位，染色体的编码长度为所有投料品种的总数，基因位越靠前表示品种越优先投产，适应度函数为改机代价，终止条件为限定迭代次数，在每次迭代过程中，选择改机代价最小的个体作为最佳个体。实验中，基于GA 的智能投料控制策略的各个参数设置如下：种群规模为100，交叉因子为0.9，变异因子为0.2，进化代数为80；算法计算过程中分别采用轮盘赌选择、线性次序交叉和基因逆序变异。

表5 规模10周计划投产信息

续表6

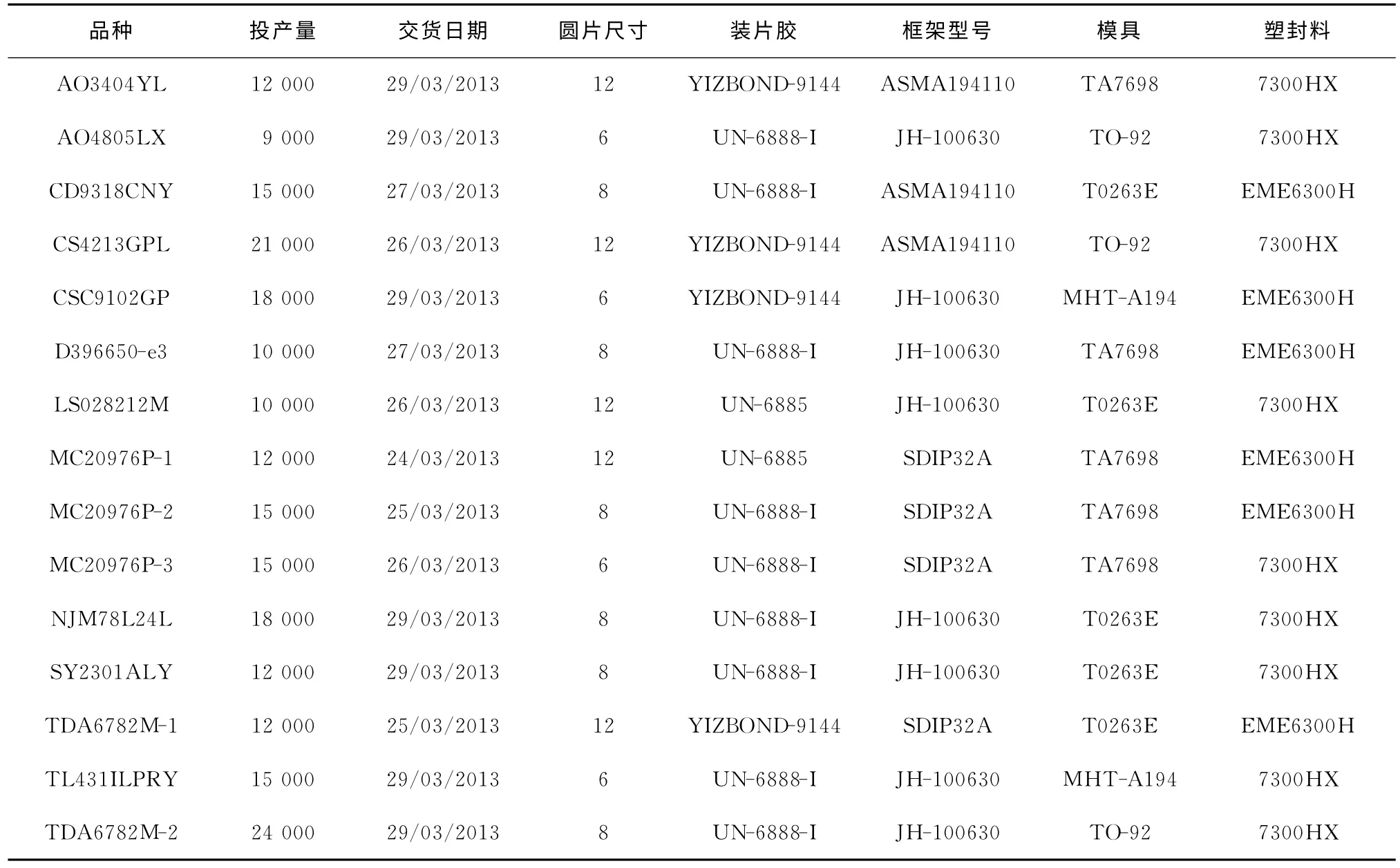
表6 规模15周计划投产信息

分别对投产品种个数和产能类型个数为（10，3）（15，3）（10，5）（15，5）的规模，采用基于品种平均分配的投料策略、基于投产量平均分配的投料策略、基于GA 的智能投料控制策略和本文提出的基于聚类的综合投料控制策略进行投料生产过程仿真，实验结果如表7所示。由表中数据比较得知，基于品种聚类的投料策略比基于GA 的智能投料策略和常规的企业投料策略，能够更好地减少改机时间代价，缩短生产周期，从而提高生产效率；在产能类型较多的情况下，该方法更能体现其优越性。上述研究给定规模较小，实际半导体生产企业中的周投产品种一般达上千种，基于聚类的综合投料控制策略在规模庞大的实际应用中更能发挥其优越性，如在背景企业中，采用该投料控制策略后，生产周期缩短了约20h，即改机时间代价降低了约20h。

表7 实验结果比较

5 结束语

本文以某半导体封装测试企业为研究背景，根据企业需求，针对粗日投料控制问题进行研究，提出一种基于K-modes聚类的投料控制综合策略。该策略首先对周计划投产品种进行聚类分析，然后依据聚类结果进行基于品种平均分配和投产量平均分配的综合策略，确定日投产品种和数量。该策略能够降低半导体封装测试生产过程中的改机时间代价，提高设备利用率，缩短生产周期，从而提高生产效益。下一步将依据聚类为基础的粗日投料控制结果，对半导体封装测试的细日投料控制问题进行详细研究。

［1］LI You，JIANG Zhibin，LI Na，et al.A review on release polices in semiconductor wafer fabrication system［J］.Industrial Engineering and Management，2011，16（6）：108-114（in Chinese）.［李 友，江志斌，李 娜，等.晶圆制造系统投料策略综述［J］.工业工程与管理，2011，16（6）：108-114.］

［2］SPEARMAN M L，WOODRUFF D L，HOPP W J.CONWIP：apull alternative to kanban［J］.International Journal of Production Research，1990，28（5）：879-894.

［3］WU Qidi，QIAO Fei，LI Li，et al.Semiconductor manufacturing system scheduling［M］.Beijing：Publishing House of Electronics Industry，2006：102-104（in Chinese）.［吴启迪，乔 非，李 莉，等.半导体制造系统调度［M］.北京：电子工业出版社，2006：102-104.］

［4］AURAND S S，MILLER P J.The operating curve：a method to measure and benchmark manufacturing line productivity［C］／／Proceedings of IEEE／SEMI Advanced Semiconductor Manufacturing Conference.Washington，D.C.，USA：IEEE，1997：391-397.

［5］GLASSEY C R，MAURICIO G C.Closed-loop job release control for VLSI circuit manufacturing［J］.IEEE Transactions on Semiconductor Manufacturing，1988，1（1）：36-46.

［6］LIU W，CHUA T J，CAI T X，et al.Practical lot release methodology for semiconductor back-end manufacturing［J］.Production Planning &Control，2005，16（3）：297-308.

［7］RYOHEI T，NOBUTADA F，KANJI U.Lot release control using genetics based machine learning in a semiconductor manufacturing system［C］／／Proceedings of the 9th International Conference on Intelligent Autonomous Systems.Amsterdam，the Netherlands：IOS Press，2006：497-506.

［8］CHUA T J，LIU M W，WANG F Y，et al.An intelligent multi-constraint finite capacity-based lot release system for semiconductor backend assembly environment［J］.Robotics and Computer-Integrated Manufacturing，2007，23（3）：326-338.

［9］HAN J，KAMBER M.Data mining：concepts and techniques［M］.San Francisco，Cal.，USA：Morgan Kaufmann Publishers，2001：233-234.

［10］LI Dazi，QIAN Li，JIN Qibing，et al.Modified global Kmeans algorithm and its application to data clustering［J］.Information and Control，2011，40（1）：100-104（in Chinese）.［李大字，钱 丽，靳其兵，等.改进的全局K-means算法及其在数据分类中的应用［J］.信息与控制，2011，40（1）：100-104.］

［11］HUANG Z.Extensions to the k-means algorithm for clustering large data sets with categorical values［J］.Data Mining and Knowledge，Discovery，1998，2（3）：283-304.

［12］ZHAO Heng，YANG Wanhai.Fuzzy K-modes clustering algorithm based on attributes weighted［J］.Systems Engineering and Electronics，2003，25（10）：1299-1302（in Chinese）.［赵 恒，杨万海.基于属性加权的模糊K-modes聚类算法［J］.系统工程与电子技术，2003，25（10）：1299-1302.］