C75混凝土动态层裂强度试验研究
王志亮,李 洋,阳 栋
(1.同济大学 地下建筑与工程系,上海 200092;2.同济大学 岩土与地下工程教育部重点实验室,上海 200092)
高强混凝土作为一种新的建筑材料,以其密度大、孔隙率低、抗压强度高等特点被广泛应用于大坝、核电站与防护工程中,而这些建筑物在承受静态载荷的同时,往往需要面对地震、风载荷、新型武器打击等动载荷的威胁.众所周知,混凝土的抗拉强度要远小于其抗压强度,两者单轴强度之比为0.07~0.11[1].在现行的设计规范中,对混凝土的抗拉强度重视不足.在动荷载作用下,混凝土的抗拉强度会显著提高[2-3].因此,研究高强混凝土的动态抗拉强度,对探究混凝土的动态力学性质和获取数值模拟所需参数都有参考价值.
层裂(spalling)是当压力脉冲在杆或板的自由面反射形成拉伸脉冲时在邻近表面的某处造成相当高的拉应力,一旦满足某动态断裂准则,则该处材料发生破裂的现象[4],这种现象在混凝土建筑物受冲击载荷时经常发生.因此,研究混凝土的层裂强度有着非常重要意义.Klepaczho[5]等提出了一套较为完善的测量脆性材料层裂强度的试验方法,通过压杆上的3组应变片测得的入射和反射信号获得进入试件中的波形,从而得到混凝土的层裂强度.该方法计入了波形弥散造成的影响,但未考虑应力波在混凝土材料中的衰减情况;Díaz-Rubio[6]等对 陶瓷材料进行层裂试验,对假定的准确性进行了分析,并验证了Klepaczho试验方法的可靠性;Schuler等[7]在原有层裂试验方法的基础上,通过在混凝土试件末端增加加速度计的方法,获得了混凝土的断裂能,为数值模拟提供了必要的参数;张磊[8]通过在试件上粘贴应变片以及增加尼龙吸收杆的方法,提出了一种新的层裂试验方法;Lu等[9]对混凝土类的拉伸理论和试验进行了总结,并发展了一种微力学模型,证明了应变率效应是混凝土材料的真实性质;Wang和Rong等[10-11]也分别对钢纤维混凝土、活性粉末混凝土进行了层裂试验,并分析了这些材料的层裂特性.可见,层裂试验作为一种研究混凝土动态拉伸性能的方法,正日益受到国内外学者的广泛关注.
本文在胡时胜等[12]工作的基础上,提出了一种新的测定应力波在混凝土中衰减规律的方法,研究了C75 混凝土的动态层裂现象以及抗拉强度的应变率效应,以期为相关工程实践提供参考.
1 试样制备及试验设备
水泥为上海金山水泥厂生产的万安牌P·Ⅱ42.5水泥;细骨料为细度模数为2.65的中砂;粗骨料为粒径5~10mm 石子;自来水,减水率(质量分数)为25%的萘系高效减水剂.水灰比(质量比)为0.38,砂率(质量分数)为48%,混凝土各组分的质量比为:m(水泥)∶m(水)∶m(砂)∶m(石子)∶m(减水剂)=1.00∶0.38∶2.41∶2.61∶0.01.按配合比配置好各组分,然后向搅拌机中依次添加沙、水泥和石子.先用搅拌机干拌1min,接着将称好的减水剂加入水中,边加水边搅拌2min.然后,将搅拌好的混凝土装入试模,用小型振动棒捣实,直到出浆为止,抹平表面,并用薄膜覆盖.24h后拆模,放入温度为(20±2)℃,相对湿度为90%以上的标准养护室中养护28d.C75混凝土的基本物理力学性能见表1.

表1 C75混凝土基本物理力学参数Table 1 Parameters of C75concrete
层裂试验采用变截面Hopkinson杆(见图1),直径74mm,试样长度为1 000mm,直径为70mm.为防止试样表面孔洞等对信号采集的影响,在拟贴应变片地方预先打磨出0.5cm×2.0cm 的平台,之后再粘贴应变片.为了减小入射脉冲的长度,防止应变片记录信号时入射脉冲和反射脉冲的叠加,测试中采用70mm 的短子弹打击入射杆.而且,短子弹产生的脉冲接近于半周期正弦波,其频带较窄,从而可有效减小波形的弥散现象[11].
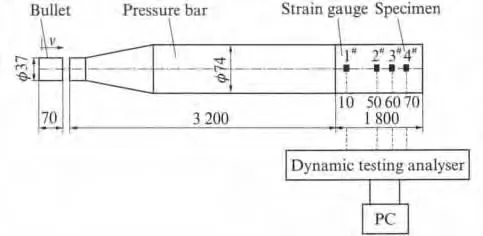
图1 试验原理示意图Fig.1 Schematic of experiment principle(size:mm)
2 试验结果及分析
2.1 不同子弹速度下的动弹性模量混凝土波速c0采用下式计算:

式中:Δl表示任意2个应变片之间的距离;Δt为对应2测点信号到达的时间差.
动态弹性模量Ed与混凝土初始密度ρ0 的关系为:

试验结果表明,随着弹速的提高,c0值从4 123.7m/s增大至4 296.0m/s,动态弹性模量为39.40~42.78GPa.
2.2 应力波的衰减规律
混凝土材料具有一定的黏弹性特性,已有研究表明,对于黏弹性材料,弹速越大,应力波在传播过程中的弥散就越严重[13].图2为弹速最大(13.43m/s)时的应力波形.由图2可见,应力波在传播了400mm后(1#和2#应变片间距为400 mm),波形变化不大.因此,本次试验暂不计入弥散对应力波形造成的影响,只考虑波峰值的衰减情况.
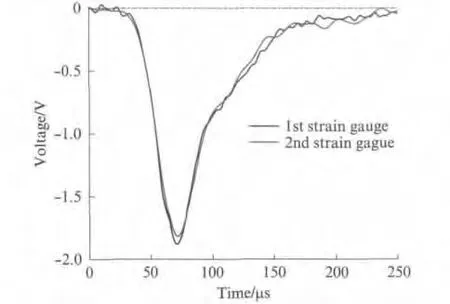
图2 应力波形弥散现象Fig.2 Wave dispersion phenomenon
应力波在混凝土中呈指数衰减,可用下式描述[2]:

式中:σ0为1#应变片对应的峰值应力;α 为衰减系数;l为应变片距离撞击端的长度;x 为断裂面到自由面距离.
在层裂试验中,如何获得应力波衰减规律至关重要.试验过程中,常常根据试样上不同位置应变片信号的衰减情况,拟合出形如式(3)的规律.但遗憾的是,本次试验数据很难拟合出理想的结果,有时甚至会出现应变信号增大的情况,如图3所示.具体原因分析如下:
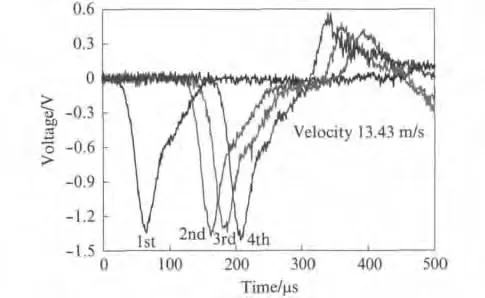
图3 4个应变片处记录的波形Fig.3 Recorded signals at four gauges
(1)试样的不均匀性.混凝土的缺陷随机分布,当压应力波通过缺陷较大的部分时,可能使微孔洞闭合,造成应变异常;(2)应变片之间的差异性,包括应变片在生产过程中的差异及粘贴过程中引起的差异;(3)试样长度因素.根据文献[14],应力波在混凝土中的衰减很微弱,衰减系数α=-0.077 7m-1.假设试样上任意部位都能接收到完整的应力波峰值信号,那么在1.0m 长的试样末端,应力波峰值大约衰减7%,反映到电压信号上大约为0.09V.在试验过程中,由于噪声的干扰,这样微小的变化很难测出.因此,很难通过试样上不同位置的应变片信号拟合出应力波的衰减规律.
针对上述问题,本文提出了一种快速、简便确定应力波衰减系数的方法.假定应力波在压缩和拉伸时的衰减规律相同,因此可对试件进行低弹速冲击,让应力波在试样两端面间来回反射传播,之后对不同距离的峰值信号进行拟合.为了排除应变片的差异性、试样的不均匀性以及压缩波与拉伸波的叠加问题,只选取2#应变片的信号来进行分析(如图4).考虑到传播距离增大应力波形弥散较严重,只取未发生叠加的前4个应力波峰进行拟合,所得的衰减系数α=0.261 1m-1,相关系数为0.93.

图4 应力波衰减过程Fig.4 Process of stress-wave attenuation
上述确定应力波衰减系数的方法其优点在于:不需要在试样上多次贴应变片,使用的应变仪通道和数据采集通道也相对较少,这可弥补试验条件的不足.此外,应力波衰减信号也更加容易获得和拟合,得到的衰减系数较为精确.
2.3 层裂强度及应变率效应

图5 试验前后试样对比Fig.5 Comparison of specimens before and after test
按照一维应力理论,对自由面附近的压缩波和拉伸波进行叠加,然后根据断裂位置,可得到不同时刻自由面附近的应力波形图.层裂位置取断裂面离杆自由端的最大与最小距平均值.图6为子弹速度10.89m/s时未考虑衰减的应力波形叠加图.根据式(3)乘以相应的衰减系数,得到试样的层裂强度σtd=18.7 MPa.而对应的加载应变率可由下式确定:

式中:Δt为拉应力波的上升时间.
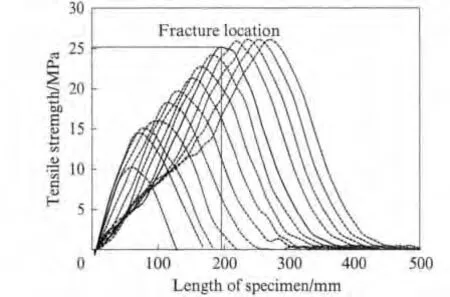
图6 应力波形叠加Fig.6 Superposition of waveform
层裂强度与应变率的关系如图7所示.由图7可见,C75混凝土具有较大的应变率效应,随着应变率的提高,其抗拉强度增强,且与应变率呈线性关系.值得注意的是:当入射压应力波强度很高时,会对混凝土造成压缩损伤,导致层裂强度试验值失真[15],因此,尽管层裂试验能反应真实的拉伸情况,但对于分析混凝土的应变率效应还存在一定的局限性.
可用动态增强因数(DIF)描述混凝土的应变率效应,其表达式为:

式中:σts表示应变率为10-6s-1时的抗拉伸强度.
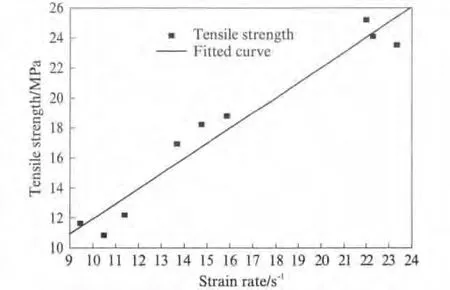
图7 层裂强度与应变率的关系Fig.7 Relation of spalling strength and strain rate
图8是混凝土单轴抗压强度为75MPa时的拉伸动态增强因数,其中的3条曲线为文献[16]修正的DIF变化曲线,对应的混凝土单轴抗压强度分别为30,60,70 MPa.从图8 可见,当应变率为100~102s-1时,混凝土的抗拉强度随应变率增加显著提高,与文献[10]中的试验结果一致.

图8 混凝土拉伸动态增强因数Fig.8 Dynamic increase factor for concrete in tension
3 结论
(1)采用低弹速冲击,对单个应变片采集到的应力波峰值进行拟合得到的衰减系数比较准确可靠,此方法可以排除试样不均匀性、应变片间差异及衰减微弱等影响,对试验条件要求也较低.
(2)C75混凝土的拉伸强度具有较强的应变率相关性,在0~102s-1应变率范围内,其抗拉伸强度随应变率呈线性增长.
(3)层裂试验能够反映真实的拉伸状态,是测量混凝土动态拉伸强度的有效方法,但获得的应变率范围较窄,对于研究混凝土的应变率范围具有一定的局限性.
[1]METHA P K.混凝土结构、特性和材料[M].上海:同济大学出版社,1988:1-50.METHA P K.Concrete structure,property and material[M].Shanghai:Tongji University Press,1988:1-50.(in Chinese)
[2]BRARA A,KLEPACZKO J R.Experimental characterization of concrete in dynamic tension[J].Mechanics of Materials,2006,38(3):253-267.
[3]WU Shengxing,CHEN Xudong,ZHOU Jikai.Tensile strength of concrete under static and intermediate strain rates:Correlated results from different testing methods[J].Nuclear Engineering and Design,2012,250:173-183.
[4]王礼立.应力波基础[M].2版.北京:国防工业出版社,2005:1-152.WANG Lili.Foundation of stress waves[M].2nd ed.Beijing:National Defense Industry Press,2005:1-152.(in Chinese)
[5]KLEPACZHO J R,BRARA A.An experiment method for dynamic tensile testing of concrete by spalling[J].International Journal of Impact Engineering,2001,25(4):387-409.
[6]DÍAZ-RUBIO F D,PÉREZ J R,GÁLVEZ V S.The spalling of long bars as a reliable method of measuring the dynamic tensile strength of ceramics[J].International Journal of Impact Engineering,2002,27(2):161-177.
[7]SCHULER H,MAYRHOFER C,THOMA K.Spall experiments for the measurement of the tensile strength and fracture energy of concrete at high strain rates[J].International Journal of Impact Engineering,2006,32(10):1635-1650.
[8]张磊.混凝土层裂强度的研究[D].合肥:中国科技大学,2006.ZHANG Lei.The study on the spall strength of concrete[D].Hefei:University of Science and Technology of China,2006.(in Chinese)
[9]LU Y B,LI Q M.About the dynamic uniaxial tensile strength of concrete-like materials[J].International Journal of ImpactEngineering,2011,38(4):171-180.
[10]WANG Zhiliang,ZHOU Nianqing,WANG Jianguo.Using Hopkinson pressure bar to perform dynamic tensile tests on SFRC at medium strain rates[J].Magazine of Concrete Research,2012,64(8),657-664.
[11]RONG Zhidan,SUN Wei.Experimental and numerical investigation on the dynamic tensile behavior of ultra-high performance cement based composites[J].Construction and Building Materials,2012,31:168-173.
[12]胡时胜,张磊,吴海军.混凝土材料层裂强度的实验研究[J].工程力学,2004,21(4):128-132.HU Shisheng,ZHANG Lei,WU Haijun.Experiment study on spalling strength[J].Engineering Mechanics,2004,21(4):128-132.(in Chinese)
[13]郭历伦.粘弹性杆中波传播的数值模拟和实验研究[D].绵阳:中国工程物理研究所,2005.GUO Lilun.Computational simulation and experimental research on wave propagation in viscoelastic bars[D].Mianyang:Chinese Academy of Engineering Physics,2005.(in Chinese)
[14]郭弦.冲击作用下混凝土中应力波传播规律研究[D].长沙:国防科技大学,2010.GUO Xian.Stress wave propagation in concrete structures under impact loading[D].Changsha:National University of Defense Technology,2010.(in Chinese)
[15]ZHANG L,HU S S,CHEN D X,et al.An experimental technique for spalling of concrete[J].Experimental Mechanics,2009,49(4):523-532.
[16]LAMBERT D E,ROSS C A.Strain rate effects on dynamic fracture and strength[J].International Journal of Impact Engineering,2000,24(10):985-998.

