基于最佳小波包分解和HMM 的齿轮故障模式识别

郑思来，王细洋

(南昌航空大学，南昌 330063)

0 引言

齿轮作为常见的动力传动装置之一，其特性直接影响到机械设备的性能，因此对齿轮的状态监测与故障诊断有着非常重要的意义。齿轮失效是齿轮传动难以避免的现象和最终归宿，并且是诱发机器故障的重要原因［1］。常见的故障形式包括齿轮断齿、均匀磨损和点蚀等，出现这些故障时会产生周期性脉冲冲击，从而致使齿轮振动信号产生幅值和相位的调制。由于齿轮箱工作环境复杂，齿轮啮合振动信号中的故障特征信息往往被强噪声所淹没，因此在强噪声背景下有效提取齿轮故障特征是实现齿轮故障模式识别的关键。快速傅立叶变换(FFT)［2］、小波分析、小波包、倒频谱、wigner 分布等是目前齿轮故障特征提取常用方法［3-5］。齿轮啮合振动信号是非平稳、非线性的，一些传统的方法无法提取出非常理想的故障特征。小波分析具有良好的时域局部性，得到了广泛的应用［6-7］，但是小波分析的高频分辨率较差，而小波包变换可以提供任意时间-频率分解的信号，也可以对高频和低频信号进行更精细的频率划分。

隐马尔科夫模型(HMM)作为模式识别的重要工具，具有很强的分类能力，已在语音识别等多个领域有了成功的应用，通过可观测的振动信号来估算设备的隐藏状态。Ocak 等［8］把HMM 应用到轴承故障诊断中，以AR(Auto-regressive)系数作为特征。Kunpeng Zhu 等［9］把HMM 的强大的特征分类能力用在高速精细机床的刀具磨损监控中。

针对齿轮发生故障时振动信号的主要特征，本研究采用最佳小波包分解提取特征和HMM 模式识别结合，形成了基于OWPD-HMM 故障模式识别方法。该方法首先利用时域同步平均(Timedomain synchronous average，TSA)对信号做预处理，然后进行降采样，再利用最佳小波包分解，自动选取齿轮啮合频率及倍频附近的频带信号，计算所选取频带信号的小波包系数能量及归一化处理作为最终特征向量，输入到HMM 中，构建故障模式识别器，自动对故障模式做出正确的识别。齿轮故障模式识别系统流程如图1 所示。

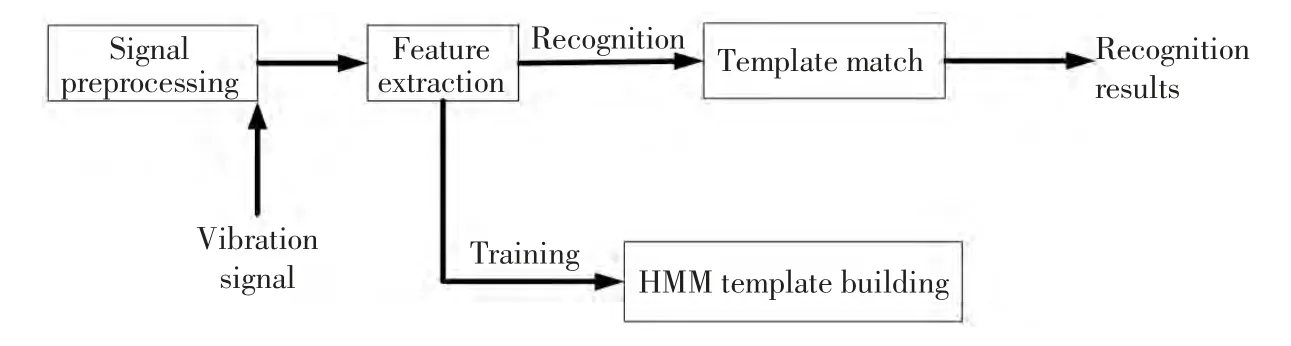
图1 齿轮故障模式识别系统流程图Fig.1 Gear fault pattern recognition system flow chart

1 能量特征的提取

本研究的齿轮故障特征的提取过程是:首先，利用OWPD 对齿轮正常、断齿、均匀磨损和点蚀数据信号进行4 层小波包分解，以获得每组数据信号的频率特征;其次，根据齿轮发生故障时的主要特征，自动选取齿轮啮合频率及其倍频附近最佳小波包基所在的频带;第三，计算最佳小波包基系数能量及归一化处理;最后，把能量特征向量作为输入量。基于最佳小波包分解的齿轮故障特征提取流程图如图2 所示。

图2 特征提取流程图Fig.2 Flow chart of feature extraction

1.1 小波包分解理论

小波变换(WT)把一个信号分解成低频子带(近似分量)和高频子带(细节分量)。小波包分解(WPD)的特性与WT 类似，都具有多分辨率分析(Multi-resolution analysis，MRA)［10］的功能。两者的主要区别是，WPD 可以对多分辨率分析没有细分的高频部分再进行划分，根据分析信号的特征，自适应的选择相应频带，与分析信号频谱相配，因此WPD 提高了时频分辨率。正交小波包的递推公式为［11］

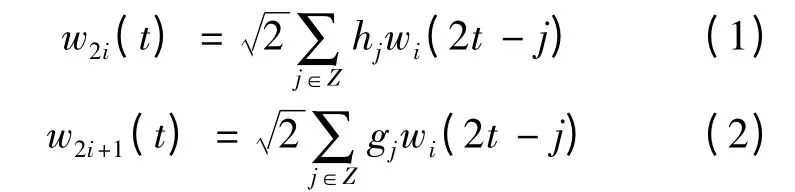
其中，hj和gj是多分辨率分析中的滤波器系数，w2i(t)和w2i+1(t)分别是尺度函数和小波母函数。小波包系数如下:

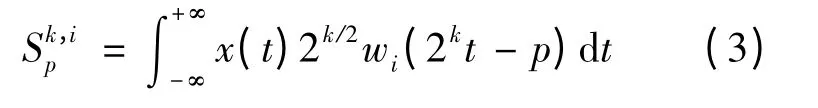
其中，x(t)、k、p 和i 分别是振动信号、尺度指标(频域参数)、位置指标(时间参数)和振荡次数。

1.2 基于OWPD 的自动提取特征

齿轮故障模式识别的特征提取过程是根据特征向量之间的差异识别不同的故障模式。基于最佳小波包分解提取齿轮故障特征的基本思想是根据齿轮发生故障时啮合振动信号的主要频率特性，对信号进行小波包分解，自动选择具有明显特征的频带，使频带在不重叠的前提下，用不同的子频带组合去覆盖整个频带。

1.2.1 自动选取最佳小波包基和频带划分

从齿轮故障机理分析来看，齿轮发生故障时，在运行中产生的振动信号的啮合频率及啮合频率的高次谐波的幅值明显增大，阶数越高，幅值增大的幅度越大，其小波包分解后计算得到的小波包基能量相应增大，在其附近频带的小波包基能量也明显增大。自动选取最佳小波包基及频带划分过程如下:

1)对信号进行傅立叶变换，观察频谱中比较明显的特征峰值，确定并设置降采样的频率为f，根据Nyquist 采样定理，其信号的频率范围为0～计算齿轮啮合频率fs:

其中，Z 为主动轮齿数，n 为电机转速。Z=21，n=1 750 r/min，f=5 120 Hz;因此，齿轮的啮合频率为613 Hz，相应的二倍频和三倍频分别为1 226、1 839 Hz。

2)对信号进行四层Daubechies 小波包分解，得到16 个节点(4，j)，其中j=0，1，2，…，15。

3)根据齿轮发生故障时啮合频率及二倍频的附近是故障主要特征出现的位置，计算每个节点的频带宽度Δf 及确定最佳小波包基的位置。

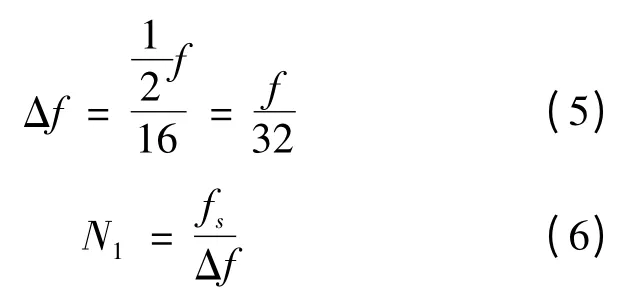
式(6)中N1向下取整。

通过以上计算自动选取6 个最佳小波包基的位置为(4，N1-1)，(4，N1)，(4，N1+1)，(4，N2-1)，(4，N2)，(4，N2+1)。

4)选取频率低于fs和高于2fs的2 个频带，其对应的最佳小波包基节点分别是(3，0)和(1，1)。

最终得到的最佳小波包分解树如图3 所示。

经过最佳小波包分解得到对应的最佳小波包基的节点分别为(3，0)、(4，2)、(4，3)、(4，4)、(4，5)、(4，6)、(4，7)、(1，1)。这8 个节点覆盖了不同频率成分的整个振动信号带宽，各个节点所包含的频率分布范围如表1 所示。

完成了对齿轮振动信号的整个频带的非均匀自动划分后，分别从低频到高频连续提取各个节点的系数，则齿轮啮合振动信号可在最佳小波包基下分解为8 个不重叠的子频带的小波包系数:

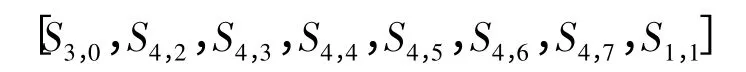
这8 个信号可以表征齿轮故障振动信号在不同频带的信号特点，但小波包系数矩阵的维数很大，为了减少维数，选择自动选取的8 个最佳小波包系数的能量值作为信号的特征，该能量值基本包括了齿轮啮合频率及其倍频。

图3 最佳小波包分解树Fig.3 The best wavelet packet decomposition tree

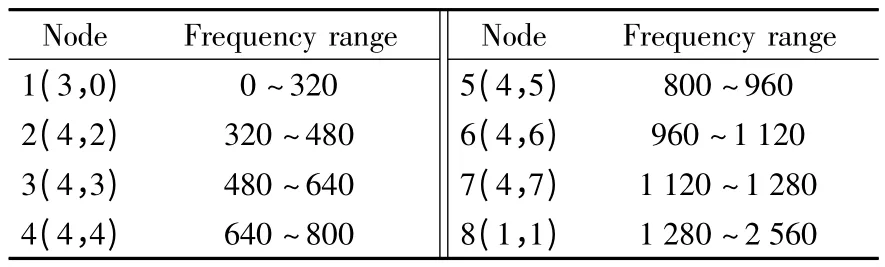
表1 各频段包含的频率范围Table 1 Frequency range Hz

1.2.2 最佳小波包系数的能量及其归一化

考虑到小波包系数的尺度相对比较高，为了得到较低维度的特征，需将小波包系数的能量值作为特征向量［12］。设Ei，j为小波包系数Si，j相对应的能量，则有

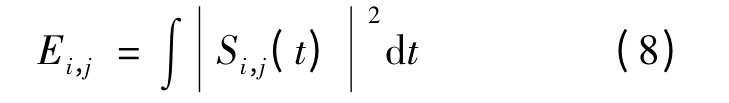
构造最佳小波包基的能量，得到小波包系数能量的初始特征向量为

对初始特征向量T 做归一化处理，有

从而得到最终特征向量

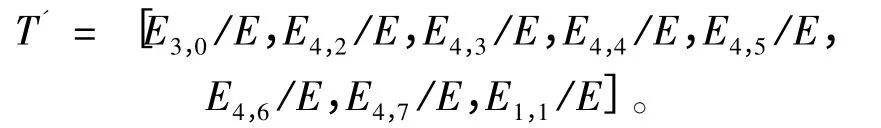
按照上述的特征提取方法，齿轮4 种模式的振动信号经过OWPD 后，各频带能量归一化的直方图如图4 所示。

从图4 可看出，对于齿轮4 种模式的振动信号，根据其故障特征基频特点进行非均匀划分频带后，每种模式的各个频带的归一化能量有着很大的区别，这为分类器做出准确的识别提供了非常好的理论依据。

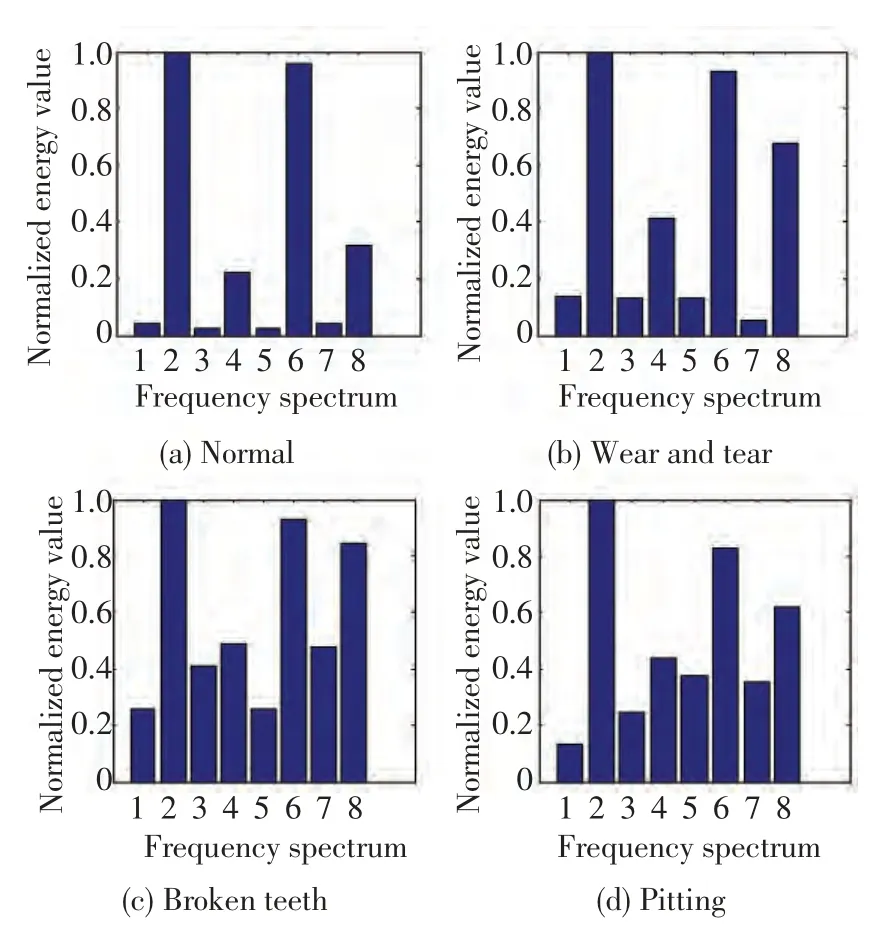
图4 4 种模式振动信号各频带归一化能量Fig.4 Normalization of frequency band energy

2 HMM 模型建立

隐马尔科夫模型(HMM)［13］是在Markov 模型的基础上发展而来的，是一个双重随机过程。HMM 是一个统计学模型，也是一个双重随机过程。HMM 中包含有限个隐状态，每个状态可根据观测量的分布产生对应的观测量。HMM 模型通常采用λ=(A，B，π，N，M)进行描述，其中，A 表示状态转移概率矩阵，HMM 模型状态变换只有两种可能:要么状态不变，要么变到相邻的下一个状态;B 表示输出概率密度函数;π 表示每个状态起始概率向量，一般情况第一个状态初始概率为1，其他均为0;N 表示模型状态，文中选用识别效果较好的个数4;M 表示每个隐状态对应的可能特征向量数目。具体模型参数见文献［14］。

在建立HMM 时候，(π，A，B)3 种概率分布都是未知，需要对模型进行训练，根据训练后的模型概率参数对4 种模式状态进行识别。HMM 有3种基本的算法:给定一个有序观测序列O={O1，O2，…，OT}和模型λ，采用前向-后向算法有效的计算出观测序列在给定模型λ 下的概率p(O/λ);采用Viterbi 算法根据系统输出的观测序列O，搜索出使得状态转移序列q=(q1，q2，…，qT)产生观测序列O 的可能性最大;采用Baum-Welch 算法进行参数估计，得到各种模型的参数。本研究用一阶齐次HMM 描述隐状态，假设提取的特征向量彼此相对独立，4 个模型代表4 种状态模式。采用EM(Expectation Maximization)算法为正常模式和故障模式建立对应模型。图5 给出了基于OWPD 特征提取的HMM 模式识别过程。

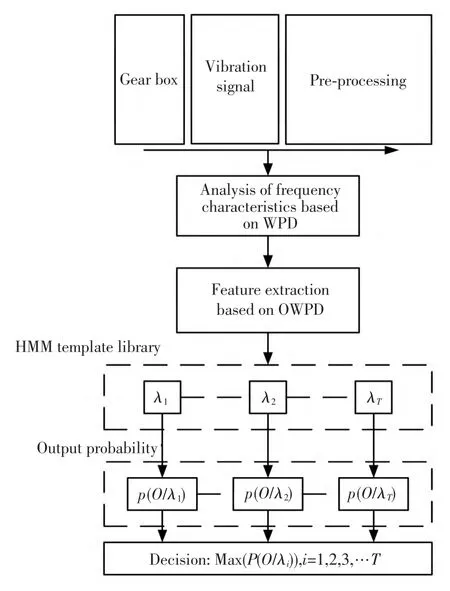
图5 基于OWPD 特征提取的HMM 模式识别Fig.5 Feature extraction and HMM based diagnostic model

3 试验过程及分析

通过分析单机减速齿轮箱的振动数据来验证OWPD-HMM 故障模式识别方法的有效性。分别采集齿轮断齿、均匀磨损、点蚀3 种常见故障数据，同时采集一组齿轮正常数据作为对比。齿轮故障诊断试验台如图6 所示，中间为单级齿轮减速箱，左边连接额定功率为4.5 kW 的交流电动机，右边为负载电机，其中还有加速度传感器、光电编码器、扭矩传感器和速度传感器等。

对齿轮3 种故障模式在试验台上进行模拟实验，预加扭力为735 N·m，采样频率为20 kHz，数据每隔10 min 采集一次，每次采集宽度为10 s，信号通过10 倍增益、A/D 转换，最后数据按照一定格式存储。

图6 齿轮故障诊断试验台Fig.6 Gear fault diagnosis experiment platform

采集到的齿轮正常数据文件122 个、断齿数据文件112 个、均匀磨损数据文件168 个、点蚀数据文件180 个。每种模式数据文件分为两半，一半用于HMM 训练，一半用于验证。把一半数据文件的原始振动信号经过预处理和采用WPD 分析频率特征，然后采用OWPD 提取每种模式的最佳特征向量。把提取的特征向量作为训练数据，模型状态数N=4，最大迭代步数为25，算法收敛误差为0.000 1。模型训练的迭代步数和迭代的对数似然概率如图7 所示。

用于验证的数据经过预处理，OWPD 特征提取，先生成观测序列，然后输入到各个已训练好的HMM 模型中进行测试，测试结果如表3 所示。从表3 中可知，在有限次的实验测试中，出现误诊的次数极少，例如在齿轮均匀磨损的84 次诊断中，正确诊断次数为82 次，1 次误诊为齿轮正常，1 次误诊为齿轮点蚀，识别率为97.61%。识别结果较理想。

在其他故障诊断中，出现误诊的次数也相对较少，诊断平均成功率达到了95.4%，在实际齿轮故障诊断中通过多次采集数据和诊断，该方法基本可以确定齿轮的故障模式，故障诊断精度高。

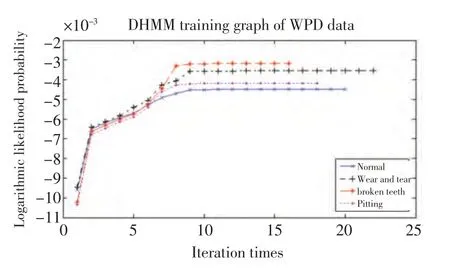
图7 HMM 参数训练迭代过程Fig.7 Training graph of HMM

表2 模式识别结果Table 2 Result of experiment

4 结论

1)利用最佳小波包分解方法可以快速准确地自动提取齿轮的最佳特征向量。

2)基于最佳小波包分解的特征提取方法有着更好的分类效果。

3)最佳小波包分解和隐马尔科夫模型结合的方法用于齿轮故障模式识别非常有效，诊断准确率高。

［1］丁康，李巍华，朱小勇.齿轮及齿轮箱故障诊断实用技术［M］.北京:机械工业出版社，2006:1.

［2］Corinthios M J.A fast Fourier transform for high-speed signal processing［J］.Computers，IEEE Transactions on，1971，C-20(8):843-846.

［3］唐曦凌，梁霖，高慧中，等.结合连续小波变换和多约束非负矩阵分解的故障特征提取方法［J］.振动与冲击，2013，32(19):7-11.

［4］宋平，文妍，谭继文.基于小波包分解和SVM 的齿轮箱故障诊断［J］.机床与液压，2013，41(21):160-163.

［5］赵怀璧，王林.基于Hilbert 解包络及倒频谱分析的齿轮箱断齿故障诊断研究［J］.煤矿机械，2011，32(5):232-234.

［6］Selesnick I W，Baraniuk R G，Kingsbury N G.The dual-tree complex wavelet transform［J］.Signal Processing Magazine，IEEE 2005，22 (6):123-151.

［7］Zhu K，San W Y，Hong G S.Wavelet analysis of sensor signals for tool condition monitoring:a review and some new results［J］.International Journal of Machine Tools ＆ Manufacture，2009，49(7-8):537-553.

［8］Ocak H，Loparo K A.A new bearing fault detection and diagnosis scheme based on hidden Markov modeling of vibration signals［C］.2001 IEEE International Conference on Acoustics，Speech，and Signal Processing，2001:3141-3144.

［9］Zhu K P，Wong Y S，Hong G S.Multi-category micro-milling tool wear monitoring with continuous hidden Markov models［J］.Mechanical Systems and Signal Processing，2009，23(2):547-560.

［10］Mallat S G.A theory for multiresolution signal decomposition:the wavelet representation［J］.Pattern Analysis and MachineIntelligence，IEEE Transactions on，1989，11(7):674-693.

［11］葛哲学.小波包分析理论与MATLAB R2007 实现［M］.北京:电子工业出版社，2007:116.

［12］许小刚，王松岭，刘锦廉.基于小波包能量分析及改进支持向量机的风机机械故障诊断［J］.动力工程学报，2013，33(8):606-612.

［13］冯长建.HMM 动态模式识别理论、方法以及在旋转机械故障诊断中的应用［D］.杭州:浙江大学，2002:22.

［14］曹端超，康建设，赵劲松，等.改进EMD 和HMM 的齿轮故障诊断方法应用［J］.噪声与振动控制，2013，33(3):208-211.