认知属性标定框架的实证研究
——以小学数学为例
高 磊,衷克定
(北京师范大学 信息技术教育研究所,北京 100875)
认知属性标定框架的实证研究
——以小学数学为例
高 磊,衷克定
(北京师范大学 信息技术教育研究所,北京 100875)
在基于认知诊断理论的自适应测试中,认知属性的标定是一项非常重要的基础性工作。该文首先使用文献法对认知属性进行理论分析,探索认知属性标定的理论依据,其次在对认知属性内容进行探讨的基础上,提出认知属性标定的结构性框架,最后通过小学数学测试题对认知属性标定进行实证研究。结果表明,认知属性标定框架能有效地提高认知属性标定的效率。
自适应测试;认知属性;认知诊断
随着教育信息化的深入发展,各种学习资源不断数字化、网络化的同时,基于网络的教育评价受到越来越多的重视。目前,教育评价的主要形式是测验,而大多数测试系统都基于经典测量理论。经典测量理论只能从宏观上判断学习者的认知水平,无法对学习者知识掌握程度做精确的判断。针对存在的问题,众多研究者开始关注微观层次的测量理论,新一代的教育测量理论应运而生。这种新的教育测量理论是认知心理学、现代测量学、统计学相结合的产物。该理论试图找到学习者能力水平与试题属性之间的相互关系,通过统计学的方法,建立数学模型,以高效而精确地判断学习者的知识状态,这就是认知诊断理论。基于认知诊断理论的自适应测试采用数学模型对学习者的知识、技能和认知状态进行诊断性测试,最终得到学生的知识掌握状态,可为教师和学习者提供针对性的信息,对教学和学习具有重要的指导意义。基于认知诊断理论的自适应测试受到越来越多研究者的关注。然而,认知诊断理论现在仍处于发展阶段,很多问题仍有待解决。认知属性的标定是进行自适应测试,进而诊断被试认知状态的基础,代表了测试内容所考察的认知成分,是认知诊断自适应测试研究的重要内容。
一、问题的提出
认知诊断理论采用统计学的方法,将被试的认知能力与测试题难度建立数学模型,挖掘认知加工信息,诊断被试的知识状态。基于认知诊断理论的自适应测试不仅能对个体绩效的强弱进行判定,更为重要的是能够提供测试者在解决问题时呈现出来的知识状态和处理技能方面的信息。因此,在测试之前必须首先对测试题考察的知识和技能进行量化分析,变为数学语言,这样才能在相应数学模型的基础上进行分析与诊断,而这个过程就是认知属性标定的过程。属性标定是认知诊断测试的基础,因此,属性标定的工作质量在很大程度上决定了测试的精确度。然而,在认知诊断自适应测试实践中,试题认知属性的标定大都由教师或学科专家完成,主要依据来源于自身经验,没有统一的属性标定的结构性框架。这种方式下确定的认知属性的完备性和精确性并不能得到保证。正如DeCarlo指出,Tatsuoka的分数减法认知诊断测验, 包含20个试题,这20个试题的属性标定是由自身和学科专家依据自身经验完成的,而属性认定经过20年、至少五批专家的争论,仍然不能保证标注正确[1]。同时,由于学科专家与学生在知识的掌握程度和运用效果方面存在较大差异,还必须从学生角度思考认知属性的标定的合理性。因此,在这种背景下,Tatsuoka提出验证和改进属性结构的方法——口语报告法[2]。该方法能够弥补专家与学生在认知程度上的差异,可以使属性标定更加合理化。但是,口语报告过程耗时耗力,容易造成接受困难或不愿意接受而应付了事的情况,反而会增加属性标定的不确定性。由此可见,如何有效地对认知属性进行准确标定是基于认知诊断的适应性测验亟待解决的问题。为了提高认知属性标定的准确性,本研究从认知属性的定义出发,探索认知属性标定的理论依据,构建认知属性标定的结构性框架以指导认知属性标定工作。在此基础上,通过对小学数学的内容建模为属性标定的合理性进行实证研究。
二、认知属性概念界定
对于认知属性的概念,专家学者都提出了自己的见解。Tatsuoka在尝试用规则空间方法研究认知问题时指出,认知属性即为产生式规则、程序性操作、项目类型或认知任务[3]。这观点得到了一部分学者的认可,在基于规则空间方法研究认知诊断的实践中得到了比较广泛的应用。然而,这四部分的内容更像是对属性进行的分类,此观点在操作层面上的实用性有待提高。2009年,Tatsuoka对认知属性做了进一步的阐述,明确提出,认知属性就是被试在完成任务时所必须具备的知识和信息加工技能[4]。Leighton, Gierl和Hunka的界定更为全面,他们认为属性是指完成任务时的知识结构和认知过程,包括知识、技能和策略[5]。也就是说,认知策略也可以作为考察的属性内容。加涅在研究学习结果分类时把认知策略看作一种特殊的智慧技能,认为认知策略是用于调控个体自身的学习、记忆和思维等认知过程的技能。因此,认知属性是指完成任务过程中的认知成分,可分为为知识、技能两方面内容,通过对知识和技能进行分析,从而可以得到认知属性标定的结构性框架。
三、认知属性标定的框架建构
认知属性是学生在完成任务时表现出来的知识状态和认知技能,而完成任务则是指学生分析问题、解决问题的过程。因此,标定认知属性必须从学生解决问题时的认知过程出发,找出学生解决问题过程的影响因素,在此基础上,建构认知属性标定框架。一般认为,问题解决的认知过程主要分为问题表征和解答计划执行两个阶段[6]。问题表征是指根据问题所提供的信息和自身已有的知识经验,发现问题的结构,构建自己的问题空间的过程。其主要目的是将外部物理刺激转变为内部的心理符号[7]。研究发现,问题表征质量的高低会直接影响到问题的解决[8][9]。解答计划执行阶段是实施解决方案、获取最终结果的过程,是学科领域及相关知识的应用过程。对问题解决的两个认识过程进行具体分析,找出影响学生解决问题过程中涉及到的认识因素,可为认识属性标定框架的建构提供理论依据。
问题表征说明了问题在头脑中的呈现方式、已知条件和未知条件问题、问题目标、涉及到的学科领域等信息。问题表征的认知过程主要分为三个阶段:首先,对问题的词语信息、图示、符号等静止操作材料建立起相应的心理映像,达到对问题的理解。在这个过程中,主要的心理过程是对词语信息、图示符号的内化。因此,对于词语信息等静止操作材料的表征是影响问题表征的重要因素,称之为视觉形象表征。在此基础之上, 个体需要对问题情境建立合理的表征。根据相关研究,问题情境信息构建的完整性与正确性会直接影响问题空间的合理性,从而影响到最终的问题解决。因此,问题情境表征是影响问题表征的又一重要因素。还有一点值得注意,问题描述对象之间的相互关系、条件规则等对问题解决也起着至关重要的作用。Hegarty等人在研究问题表征策略时曾经指出:问题表征的困难在于理解问题条件的相互关系上,而不在单独条件上[10]。可见,问题条件之间的关系表征是影响问题表征正确性与合理性的关键因素。综上所述,影响问题表征的主要因素为视觉形象、问题情境以及条件关系,因此,可以用这三种主要因素作为问题表征的显性描述。
问题解答则是设计答题计划并进行实施,主要涉及学科领域相关知识及其应用。在自适应测试中,问题表征是对词语信息的内化,外在表现则是对题意的理解;而问题解答则是领域知识的选择和应用,表现为知识状态的掌握程度。因此,我们应该以学科领域知识及其应用的视角考察领域知识的具体内容和外在表现。领域知识源于人工智能对知识表征的研究,把领域知识定义为某一领域的概念、概念之间的关系以及有关约束的集合。可见,是系统化的知识表征形态,结构清晰完整,特指某一特定领域的知识,属于知识范畴。而对知识的结构化划分主要有两种。一是信息加工心理学,只是分为陈述性知识和程序性知识;二是布鲁姆教育目标分类理论,把知识分为事实性知识、概念性知识、程序性知识和反省认知知识四大类。领域知识是关于某个领域的所有知识,因此,反省认知知识并不能包括在内。事实性知识和概念性知识与信息加工心理学中的陈述性知识的内涵是一致的。对于陈述性知识与程序性知识的划分方式,Alexander从认知学习角度研究领域知识时,对这种分类进行了补充,加入了条件性知识[11]。因此,领域知识可分为陈述性知识、程序性知识和条件性知识。陈述性知识是关于事物及其关系的知识,能够直接陈述,回答的是“是什么”的问题,是一种描述性知识。程序性知识则是关于完成某项任务的行为或操作步骤的知识,不能直接描述,只能借助任务或作业的完成状态间接推测事实,回答的是“怎么做”的知识。条件性知识指的是限制性的知识,即知道什么时候或在什么情境下使用这些知识的知识。学科领域知识是针对某一具体的学科的,是关于某一学科中的那些具有一定相关性、逻辑性、操作性的知识体系。根据前述分类,学科领域知识的三维结构应该包括学科内容、操作技能和问题条件三类知识。学科内容知识即为特定学科范围内的陈述性知识,包括概念、原理等描述性知识,与领域知识的陈述性知识相对应。操作技能则是指某一学科领域内的解题规则、操作程序等,属于认识技能的知识范畴,与领域知识的程序性知识相对应。问题条件则是在特定学科内容知识的适用范围、使用限制及约束规则,与领域知识的条件性知识相对应。总之,对于问题解答阶段涉及到的学科领域知识可以用学科内容、操作技能和问题条件三类知识来表示。
根据上述分析,认知属性标定须依据问题解决的认知过程,合理地确定认知成分。问题表征是语义理解阶段,由视觉形象、问题情境以及条件关系等三种影响问题表征的主要因素表示;问题解答阶段主要是具体学科领域知识应用的过程,主要由学科内容、操作技能和问题条件三类知识表示。认知属性标定的结构性框架如下图所示。在认知属性的实际操作过程中,以此框架为指导,结合具体学科内容,可以比较准确而完整地确定认知属性,从而为后续的认知诊断过程提供支持。
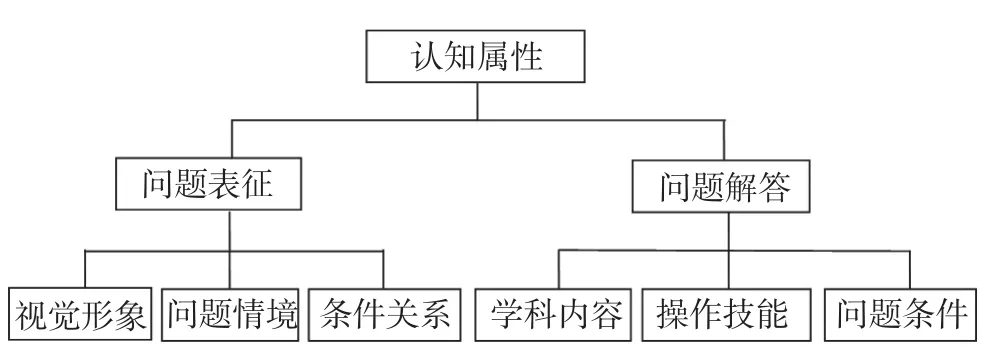
认知属性结构性框架图
四、实证研究
基于认知诊断的计算机自适应测试系统确定认知属性的目的是建构认知属性矩阵,把无法确定的心理特质转化为可以观察和测量的数据,进而通过数学建模的方法认定学生的知识掌握状态。认知属性结构是否准确、合理关系着整个测验的科学性。
认识成分可以分为语义理解和知识应用两部分内容。问题表征阶段的语义理解部分包括的情境、条件和关系,虽然与数学学科本身的知识关系不大,却是解题中至关重要的一环,因此,数学情境、条件状态、数量或视觉空间中关系可以作为三种认识属性加以标示。根据前面的分析,数学知识是指数学符号、事实,数学概念性知识,以及程序性知识。数学事实性知识包括符号、公理等不需要证明的知识,一般需要单独考察。这类知识大都作为公式推导或者课堂讲解使用,有时也作为题目的隐含条件出现,比如计算人数不可能出现小数,鸡兔同笼问题中鸡有两条腿而兔子有四条腿,这些客观事实在数学中一般不作为测试内容。数学概念性知识是人脑对现实对象的数量关系和空间形式的本质特征的一种反映形式,是数学基础知识的重要组成部分,也是学习其他数学知识的基础。数学程序性知识则是指数学算法、规则、公式、定理等。程序性知识指的是知识的应用,通常称之为数学技能,以知识状态的形式表现出来。数学技能即运用数学知识解决问题的能力,是指在数学学习过程中通过训练或练习得以完成数学任务的智力活动方式。数学技能具体包括数学知识辨识技能、数学概念应用能力、数学规则操作与应用技能、运用各种知识解决复杂问题的技能。数学是一门研究数量关系和空间形式的科学,具有严密的符号体系,独特的公式结构,形象的图像语言。数学知识,如概念、原理、公式、算法,一般都是通过技能表现出来的。例如,倒数是一个数学概念,属于数学知识。一般情况下,很少有测试直接问倒数的定义,而大部分测试却是让学生求一个具体数字的倒数来测试学生是否掌握倒数的概念。求具体数字的倒数则属于数学知识的运用,属于操作技能层面。这样,就可以判断学生是否掌握了倒数这一概念。反之,操作技能掌握的外在表现形式是学生的知识状态,我们无法看到学生技能操作的内部心理过程,但可以通过学生知识状态的变化推断学生的技能掌握程度。
本研究选取小学六年级数学上册部分内容作为研究对象,经走访一线教师,并经学科专家认定,测试主要考察内容包括:分数乘法的意义,计算法则及算法,倒数的意义及算法,分数除法的意义及算法,圆的特征及面积公式、周长公式,计量单位概念及关系换算。按照上述分类方法,结合具体内容,得出小学六年级上册知识分类表(如表1所示)。

表1 小学数学六年级上册知识分类表
由上述分类方法,以小学数学六年级上册内容为基础,得出13个属性,用A1、A2…A13表示。其中,(A1)分数的意义,(A2)通分与化简,这两类属性是新学习内容的基础,因此,测试中必定包含这两类属性。(A3)分数乘法的意义,(A5)分数除法的意义,(A7)倒数的意义,(A9)比的意义,这四项属于概念性知识。剩余的7项属性属于程序性知识,它们分别是:(A4)分数乘法运算,(A6)分数除法运算,(A8)倒数的运算,(A10)比的运算,(A11)圆的面积、周长计算,(A12)百分比运算,(A13)计量单位的换算。小学数学认知成分还包括数学情境、条件状态和数学关系,这三种元素分别标识为A14、A15和A16。
基于认知诊断的计算机自适应测试系统实体的编制以认知心理学和信息认知加工模型为基础,在认知诊断试题编制原则的指导下,以小学数学六年级上册为具体内容,编制完成25道试题。通过与一线教师进行商定,笔者完成了25道试题的属性标定,并生成项目(试题)属性关系矩阵。每一道试题都要对所有16个属性进行标识,如果试题考查了该属性则标识为1,反之,则标识为0。每一道试题通过这种方式进行标识完成后,整套试题考查的内容则通过认知属性关系矩阵表示出来。根据TatsuoKa的研究,验证认知属性合理性可采用回归分析的方法进行[12]。具体方法是通过建立项目难度对认知属性的回归,考察认知属性对项目难度的解释能力,若所认定的认知属性能解释项目难度的60%以上,则说明所认定的认知属性基本可靠。为了确定试题难度值,本研究选用项目反应理论模型中双参数逻辑斯蒂克模型,采用BILOGMG3.0软件,对项目难度值进行估算,得到各项目难度值(如表2所示)。
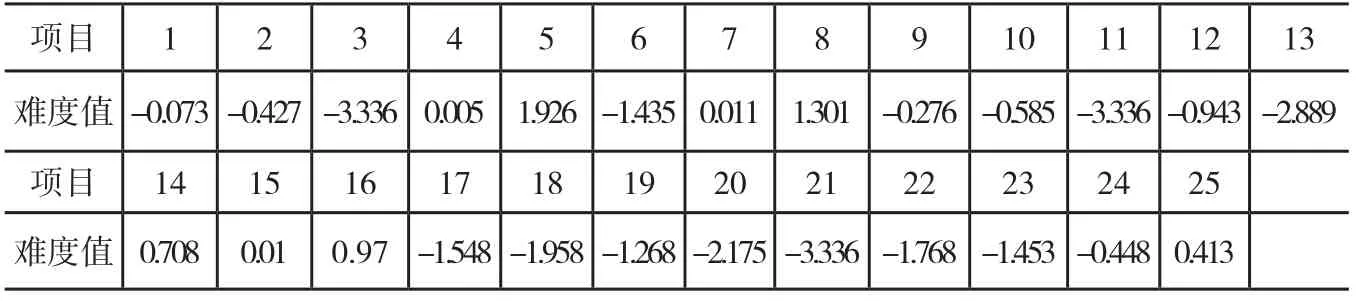
表2 项目难度值表
本研究以认知属性为自变量,以难度值为因变量,应用SPSS19.0软件进行回归分析。认知属性标定位0或1,表示项目中是否考察了该属性,若未考察,则该属性值为0,若考察了该属性,则指为1。本研究中,项目难度对属性的回归R系数为0.817,R的平方为0.667。也就是说,项目的认知属性对项目难度的解释力达到了66.7%,超过了预定的标准值60%(如表3所示)。由此可以得出,依据数学认知属性标定框架,结合该部分教学内容,由此得出的项目的认知属性基本可靠。

表3 回归分析结果
五、结束语
多数情况下,以学科教学经验为主要依据标定认知属性虽然具有一定的可操作性,但是主观性过强,认知属性标定的精确性和完备性很难得到保证。而口语报告的方法受被试样本的限制,工作量大。本文从分析问题解决的认识过程出发,确定了语义理解和知识应用两种认知成分,并进一步进行了细化,构建了认知属性标定的框架。然后,结合数学学科性质与特点,得出了认知属性结构性框架。然后,以认知属性标定框架为指导,制订了数学认知属性标定的基本框架,通过小学数学的具体学科内容进行实证研究,结果显示,试题认知属性标定是合理有效的。需要指出的是,在此框架指导下的认知属性标定未必会带来质量上的明显提升,但是在可接受范围内,标定效率得到了较大提高。认知属性标定框架指导下,认知属性标定的粒度大小可以由教师或学科专家根据测试要求灵活把握。本研究是基于认知诊断理论对认知属性标定结构性框架的一次实践,希望可以为认识诊断的试题属性标定工作提供帮助。
[1] DeCarlo, L. T. On the analysis of fraction subtraction data: The DINA model, classification, latent class sizes, and the Q-matrix[J]. Applied Psychological Measurement, 2011,(35):8-24.
[2][4][12] Tatsuoka, K. K. Cognitive Assessment: An Introduction to the Rule Space Method[M]. New York:Routlege,Taylor & Francis Group,2009.
[3] Tatsuoka, K. K. Rule Space: an approach for dealing with misconceptions based on item response theory[J].Journal of Educational Measurement, 1983, (20): 345-354.
[5] Leighton, J. P., Gierl, M. J. & Hunka S. M.The attribute hierarchy method for cognitive assessment: A variation on Tatsuoka’s rule-space approach[J].Journal of Educational Measurement, 2004,(41): 205-237.
[6] Mayer, R. E., & Hegarty M. The Process of Understanding Mathematical Problems[A]. Stemberg, R. J. & Talia Ben- eeved. The Nature of Mathematical Thinking [C].New Jersey: Lawrence EdbaUm Associates, 1996.3-25.
[7] 胥兴春,刘电芝. 问题表征方式与数学问题解决的研究[J].心理科学进展,2002,(3):264-269.
[8] Anand P G, & Ross, S. M. Using computer-assisted instruction to personalize arthmatio materiais for elementary school children[J].Journal of Education Psychology, 1987,(2): 72-78.
[9] Mayer, R. E.Thinking,problem solving, cognition(2nd ed.)[M].Newyork:W. H. Freemanand Company,1992.
[10] Hegarty, M.& Mayer, R. E, Monk, C.A. Comprehension of arithmetic word problems: A comparison of successful and unsuccessful problem solvers[J]. Journal of Educational Psychology,1995, 87(1): 18-32.
[11] Alexander, P. A, Schallert, D. L, Hare, V. C. Coming to terms: How researchers in learning and literacy talk about knowledge[J].Review of educational research, 1991, 61(3): 315-343.
高磊:在读博士,研究方向为信息技术教育、认知诊断及自适应测试(gaolei_bnu@mail.bnu.edu.cn)。
衷克定:教授,博士生导师,研究方向为教育技术理论、信息技术教育、在线学习与发展、教育信息管理(zhongkeding@bnu.edu.cn)。
2013年8月11日
责任编辑:李馨 赵云建
Empirical Study of Cognitive Attributes Calibration Framework——A Case Study of Primary Mathematics
Gao Lei, Zhong Keding
(Institute of Information Technology Education, Beijing Normal University, Beijing 100875)
Cognitive attribute calibration is a very important basic work in the adaptive test based on cognitive diagnostic theory. In this paper,firstly, cognitive attributes are analyzed by literature method and the theoretical basis of cognitive attributes calibration is explored; and then, structural framework of cognitive attributes calibration is proposed based on the exploration of cognitive attribute content; finally, empirical research is carried out through calibrating cognitive attributes of primary mathematics test items. The results show: the framework can effectively improve the efficiency of cognitive attributes calibration.
Adaptive Test; Cognitive Attribute;Cognitive Diagnosis
G434
A
1006—9860(2014)03—0019—05

