谐波谐振的模态分析法及其应用

丘 凌，丘 扬

（1.国网浙江省电力公司经济技术研究院，杭州 310008；2.国网浙江省电力公司杭州供电公司，杭州 310009）

1 概述

电力系统中大量使用的电力电子设备，如交直流整流器、电气化机车、电弧炉等，在运行时会产生高次谐波。这些设备在电力系统中的应用不断增加，已成为系统中客观存在的高次谐波源。构成电力系统的发电机、变压器、输电线路、电抗器和电容器等均为感性元件或容性元件，其参数及连接方式决定了系统的固有谐振频率。由于系统固有谐振频率不同，对各次谐波的反应或敏感程度也不相同，表现为谐波电压/电流的放大或衰减，特别当系统中的某次谐波与系统的固有谐振频率相同或接近时，会导致该次谐波严重放大，即发生谐波谐振，可能危及系统运行安全。由此可见，电力系统谐波谐振是由谐波源的激励与系统的内在特性共同造成的。因此，治理电力系统的谐波问题，不仅要消除或减少系统中的谐波源及其影响，还应防止系统固有频率与可能的谐波源频率接近甚至重合的情况。由于发现系统中的谐波源然后进行治理具有滞后性，因而通过事前了解系统的谐波谐振频率并采取预防措施应该是治理电力系统谐波问题更合理可行的途径。因此，研究电力系统的谐波谐振频率具有理论和实际意义。

计算系统谐波谐振频率的方法主要有解析法、频谱分析法、模态分析法[1-2]等，前两种方法存在计算复杂、耗时长的问题，模态分析法由于其高效方便的特点受到重视[3-5]，通过灵敏度矩阵和参与因子[6-8]等可为治理方案提供更多的信息[9-10]。但单一使用模态分析法有其局限性，仅适用于部分谐波谐振模式，不能得到全部谐波谐振频率。在有些文献中，将谐波的谐振模式划分为并联谐振和串联谐振，并认为必须分析回路阻抗矩阵才能准确获得串联谐振频率及相关支路的信息，但本文论证实际情况并非如此。文献[3]提出1个改进的模态分析法，该方法结合使用基于回路阻抗矩阵的模态分析法和虚拟支路法，可求得包括串联谐振频率在内的全部谐波谐振频率，并指出求解串联谐振问题必须使用回路阻抗矩阵的结论。文献[4]算例中求得的3个串联谐振频率实际上是与并联谐振频率完全相同的回路串联谐振频率。实际上，基于回路阻抗矩阵的模态分析法获得的是回路串联谐振频率，与基于导纳矩阵的模态分析得到的并联谐振频率完全相同，因而使用基于节点导纳矩阵的模态分析法和虚拟支路法也可求得系统全部谐波谐振频率，且计算比基于回路阻抗矩阵的方法更简化，适合实际应用。此外，为准确理解和运用，对于虚拟支路法需要更合理的解释。

2 谐波谐振的模态分析法

系统节点电压电流方程为：

式中：Y为n×n节点导纳矩阵；n为系统节点数；V=（V1，…，Vn）T和I=（I1，…，In）T分别为节点电压和节点注入电流向量。

导纳矩阵可分解为：

式中：L和T分别为左、右特征向量矩阵，且T=L-1；∧为对角特征值矩阵，如果导纳矩阵Y的n个特征值各不相同，可得：

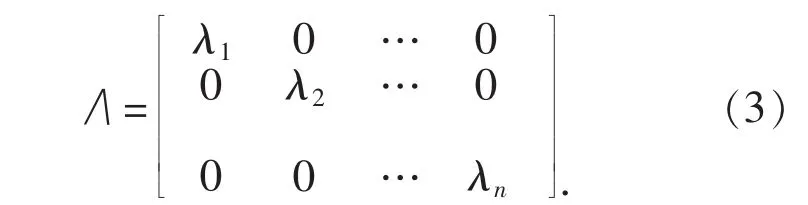
由式（1）和式（2）可得：

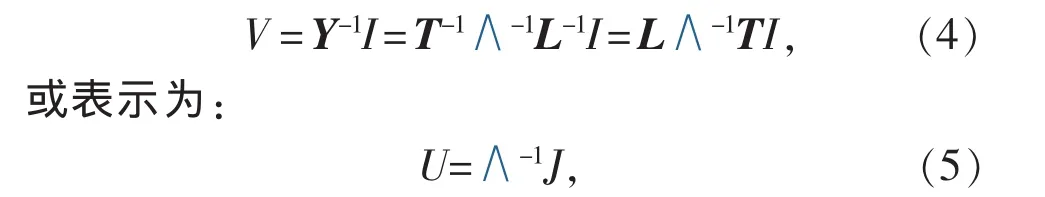
式中：U=TV定义为模态电压向量，U=（U1，…，Un）T；J=TI定义为模态电流向量，J=（J1，…，Jn）T；∧-1可称为模态阻抗矩阵。

当电网发生节点并联谐波谐振时，某些节点的注入电流将产生很高的节点电压。由式（3）和式（5）可知，如果λi等于0或很小，则很小的模态电流Ji可能导致很大的模态电压Ui。因此，可由λi等于或接近零判断并联谐振状态。实际应用时，可通过扫描发现特征值的符号改变来判断谐振点所在区间。为减少计算量，可先选择较大的扫描步长，然后不断在缩小的区间内使用较小的扫描步长，以获得足够的精度。由于导纳矩阵与阻抗矩阵的互逆关系，其特征值互为倒数，因此基于阻抗矩阵的模态分析法只能得到相同的结果，差别在于是以1/λi等于或接近零判断谐波的并联谐振状态。

对于如图1所示的3节点系统[3]，运用基于节点导纳矩阵的模态分析方法可求得3个并联谐振频率（或回路串联谐振频率）。在一些文献中，认为其余的谐波谐振为串联谐振，需通过基于回路阻抗矩阵的模态分析法求得谐振频率。但实际上，基于回路阻抗矩阵的模态分析法仅能获得回路串联谐振频率，与基于导纳矩阵的模态分析法得到的并联谐振频率完全相同，单一使用基于回路阻抗矩阵的模态分析法并不能求得支路串联谐振频率。为求取其余的串联谐波谐振频率，文献[3]提出的虚拟支路法是行之有效的，本文对此给出如下解释。

为便于说明，先忽略各支路阻抗的电阻分量。将节点i的连接支路等值为接地支路xA，当节点i的连接支路发生并联谐振，则xA→∞；当节点i的连接支路发生串联谐振，则xA=0。为模拟支路串联谐振条件xA=0，可以通过与xA并联一短接支路。在节点i上并联支路阻抗xi，可得：

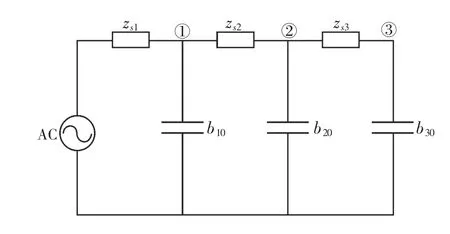
图1 3节点系统接线

当节点i发生并联谐振，须满足xA+xi=0，即为xi与xA构成回路串联谐振，可见xi与xA发生并联谐振即等同于xi与xA构成回路串联谐振，这也印证了并联谐振与回路串联谐振的一致性。运用模态分析法可求得此接线下的并联谐振频率（回路串联谐振频率），在谐振状态下须满足xA+xi=0，即：

如果并联支路电抗xi足够小，式（7）近似等于支路串联谐振条件xA=0。由此可知，通过与xA并联短接支路可以实现支路串联谐振频率计算，此短接支路即为文献[3]提出的虚拟支路。

如果计及支路阻抗的电阻分量，支路串联谐振条件可表示为 Im（zA）=0（Im（zA）表示阻抗 zA的虚部），由于系统中各支路阻抗的电阻分量一般小于电抗分量，故可近似以zA=0作为支路串联谐振条件。类似地，通过支路zi与zA并联，zi阻抗足够小，运用模态分析法求得此接线下的并联谐振频率（回路串联谐振频率），即近似等于支路zA的串联谐振频率。

综上所述，运用基于节点导纳矩阵的模态分析法和虚拟支路法，通过频率扫描可求得系统全部谐波谐振频率，且无须使用基于回路阻抗矩阵的分析方法，计算得以简化，更适合实际应用。由于导纳矩阵Y的元素为复数，谐波谐振的模态分析涉及求取复系数矩阵的特征值和特征向量，可利用标准计算机程序求得。

3 与谐波谐振的解析法结果比较

以图1所示的3节点系统为例。图中，各阻抗值均为对应于基波的阻抗值，zs1=0.02+j0.3Ω，z12=0.08+j0.3Ω，z23=j0.25Ω，b10=j0.015Ω-1，b20=j0.015Ω-1，b30=j0.07Ω-1。 可列出系统的谐振方程并求得谐振频率，为便于计算，在谐振方程中忽略了各支路阻抗的电阻分量。

并联谐振方程如下：

回路串联谐振方程如下：

支路串联谐振方程如下：

在上述公式中，符号“//”表示支路并联运算；xs1，x12，x23分别表示 zs1，z12，z23的电抗分量，x10=-1/b10，x20=-1/b20，x30=-1/b30；h表示谐振频率，单位为标幺值（p.u.）。根据计算结果，并联谐振频率与回路串联谐振频率完全相同，原因很简单，因为两端相连的并联阻抗x1与x2也可以看作是头尾相连构成的串联回路。因此，将谐振模式简单地定义为并联谐振和串联谐振并不严谨，应该区分回路串联谐振和支路串联谐振。

运用基于导纳矩阵的模态分析法对上述系统进行计算（为与解析结果比较，忽略了各支路阻抗的电阻分量），可得到3个谐振频率，分别为3.8374，16.5070和26.5192，与解析结果完全一致，可见基于导纳矩阵的模态分析法适用于并联谐振（或回路串联谐振）分析。

4 算例

对于图1所示的3节点系统，运用解析法、频谱分析法和基于节点导纳矩阵的模态分析法，谐波谐振评估计算结果示于表1，其中支路串联谐振1-3分别为与节点1-3接入虚拟接地支路后构成回路对应的支路。由于解析法、频谱分析法为精确方法，其结果可作为标准答案。由表1可见，如忽略支路阻抗的电阻分量，模态分析法结果与解析法、频谱分析法完全一致；如计入支路阻抗的电阻分量，模态分析法的误差也很小，能满足实际应用要求。系统模态阻抗示于图2，各曲线编号按其峰值出现顺序，其中曲线1，5，9为系统模态阻抗曲线，其峰值对应于系统并联谐振；曲线2，7为节点1虚拟接地时的模态阻抗曲线，模拟节点1上接入谐波电压源时的系统模态阻抗曲线，其峰值对应于相关支路（与虚拟接地支路构成回路）的串联谐振；曲线3，6为节点2虚拟接地时的模态阻抗曲线，模拟节点2上接入谐波电压源时的系统模态阻抗曲线；曲线4，8为节点3虚拟接地时的模态阻抗曲线，模拟节点3上接入谐波电压源时的系统模态阻抗曲线。

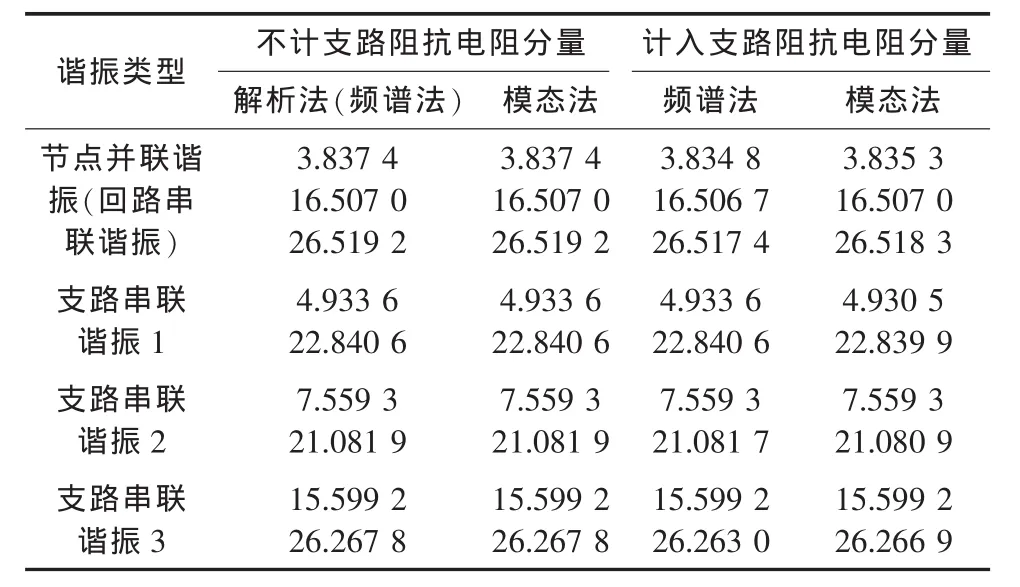
表1 系统谐振频率及分类

5 结论

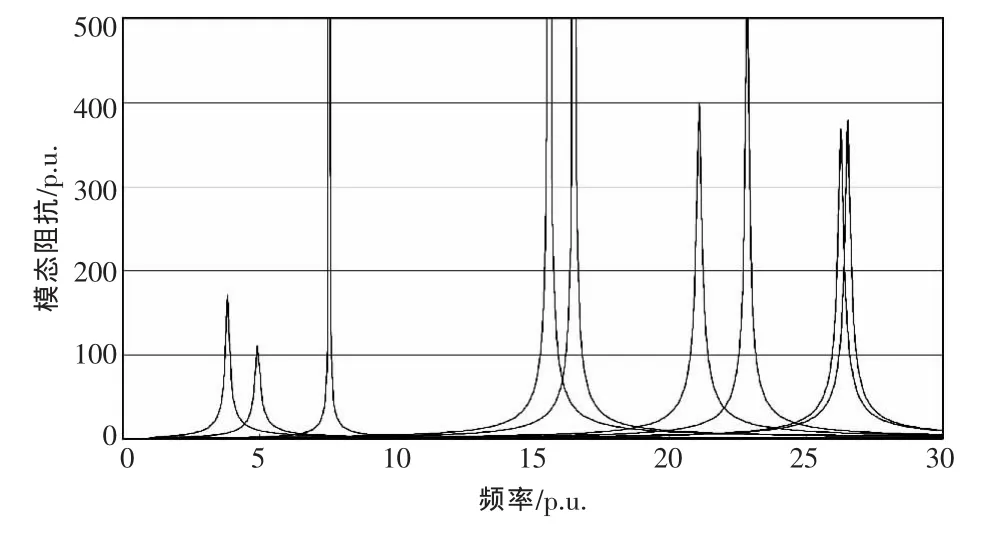
图2 系统模态阻抗曲线

基于节点导纳矩阵或基于节点阻抗矩阵的模态分析法适用于系统并联谐振分析。实际应用时，可通过扫描发现特征值的符号改变来判断谐振点所在区间。由于导纳矩阵与阻抗矩阵的互逆关系，其特征值互为倒数，因此两种方法的结果相同。

系统谐波谐振可分为并联谐振和串联谐振，串联谐振又可分为回路串联谐振与支路串联谐振。基于回路阻抗矩阵的模态分析法适用于回路串联谐振分析，由于系统回路串联谐振频率与并联谐振频率完全相同，因而与系统并联谐振分析结果相同，单一使用基于回路阻抗矩阵的模态分析法并不能求得支路串联谐振频率。

结合运用基于节点导纳矩阵的模态分析法和虚拟支路法，可以求得包括支路串联谐振频率在内的系统全部谐波谐振频率，且计算比基于回路阻抗矩阵的方法更简化和规范，适合实际应用。

[1]WILSUN XU，HUANG ZHENGYU，YU CUI，et al.Harmonic resonance mode analysis[J].IEEE Transactions on Power Delevery，2005，20（2）∶1182-1190.

[2]徐文远，张大海.基于模态分析的谐波谐振评估方法[J].中国电机工程学报，2005，25（22）∶89-93.

[3]周辉，吴耀武，娄素华，等.基于模态分析和虚拟支路法的串联谐波谐振分析[J].中国电机工程学报，2007，27（28）∶84-89.

[4]仰彩霞，刘开培，王东旭.基于回路模态分析法的串联谐波谐振评估[J].高电压技术，2008，34（11）∶2459-2462.

[5]雷之力，艾欣，崔明勇，等.基于模态评估法的微网串联谐振仿真[J].浙江大学学报（工学版），2011，45（1）∶178-184.

[6]PEREZ-ARRIAGE I J，VERGHESE G C，SCHWEPPE F C.Selective model analysis with application to electric power systems（part I）∶heuristic introduction[J].IEEE Trans on Power Apparatus and Systems，1982，101（9）∶3117-3125.

[7]周双喜，朱凌志，郭锡玖，等.电力系统电压稳定性及其控制[M].北京：中国电力出版社，2004.

[8]彭谦，马晨光，杨雪梅，等.线性模态分析中的参与因子与贡献因子[J].电网技术，2010，34（2）∶92-96.

[9]张丽莹，杨洪耕，刘亚梅.基于网络固有结构理论的集中滤波器配置[J].现代电力，2008，25（2）∶42-46.

[10]王艳松，刘军，李中树.配电网无源滤波器的优化配置[J].高电压技术，2010，36（9）∶2324-2328.