声吸收系数对声自导鱼雷作用距离影响的仿真分析❋

刘志浩 施建礼 赵祚德

（海军潜艇学院 青岛 266071）

1 引言

鱼雷自导作用距离受多种因素制约，其中海水的声吸收作用对自导距离有着重要影响。在理想水文条件中，声传播损失主要由波阵面的扩展而引起的几何衰减，介质粘滞、热传导及其他弛豫过程引起的吸收损失，海水中泥沙、气泡、浮游生物等悬浮粒子以及介质不均匀性引起的散射损失三部分组成。通过改变声吸收系数可以改变声信号的传播损失，进而改变鱼雷的自导作用距离。

2 海水对声信号的吸收

引起声强在介质中的衰减可以归纳为以下三个方面：扩展损失、吸收损失和散射［1～3］。理想介质中，沿矢径r方向传播的球面波TL可表示为

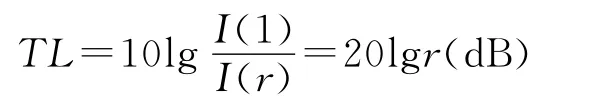
在介质中，由于吸收和散射引起的传播损失经常同时出现，当平面波传播微元距离dx后，声强降低为dI，dI应和声强I和dx成正比。声吸收引起的传播损失等于吸收系数乘上传播距离，在声球面扩散模型中，总的传播损失为

只考虑均匀介质中的经典吸收时，吸收有两种原因引起：α＝αη＋αk。αη为介质切变粘滞的声吸收系数；αk为介质的热传导声吸收系数。实际中吸收数值远大于经典吸收系数αη＋αk，它们之间差值为超吸收。由于超吸收主要与海水中盐离子的弛豫频率有关，经验公式中衰减与声波频率的平方成正比，此文中不对超吸收因素作深入描述。

3 自导鱼雷捕获目标概率

对于声自导鱼雷，自导作用距离是影响其性能的一个重要指标。在其他因素不变的情况下，自导作用距离越大，鱼雷的捕获概率越高。并且相关文献已经仿真证明了自导作用距离对鱼雷捕获概率的影响［4～5］。

目标运动到命中点时，由于运动要素存在误差，将会散布在命中点一定范围内。同样，由于鱼雷运动也存在一定的散布，其自导半径边缘也会散布在命中点附近。在命中点做垂直于目标和鱼雷相对移动线的垂线PP′轴，鱼雷扇面边缘点（相当于鱼雷）的散布在PP′轴上呈正态分布，用概率误差可表示为

同样，目标在轴上的散布为：

将PT（X）和Pm（X）两个正态分布进行综合相当于对两者概率误差进行综合，有

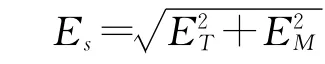
这样可以把扇面边缘上的点看做没有散布，只是目标具有概率误差为Es的散布。把扇面与目标接触点左右两侧的扇面投影到PP′轴上，得到S1、S2即为相对搜索宽度。显然只要目标出现在S1、S2遮盖的范围内，自导扇面就能发现目标。因此自导鱼雷水平面内的捕获概率就是目标出现在［S1，S2］中的概率，即有

其中ρ＝0.47694。

该式即为求解自导鱼雷是平面内捕获概率的基本关系式［6～7］。垂直面内捕获概率计算公式与水平面内相似，但由于自导鱼雷垂直面内搜索宽度很宽，鱼雷和目标在垂直面上散布误差有限，因此鱼雷在垂直面内捕获概率一般为100%。在许多要求不是很严格的地方，考核自导鱼雷捕获概率往往只需计算水平面的捕获概率即可，这样的处理结果与实际情况差别不大［8］。

4 声吸收系数对捕捉概率及自导作用距离影响的仿真分析

在声源级、检测阈等参量不变的条件下，鱼雷自导系统的作用半径与传播损失有关，传播过程中损失越大，则鱼雷自导的作用距离越短。假设只改变海水声吸收系数，其他因素保持不变，若使自导系统能检测到信号，则根据声纳方程可知传播过程中声信号的衰减应保持不变。

经实验测量，海水中声吸收系数为0.13dB／km［9～10］。仿真过程中α取值由0.13dB／km～10.13dB／km，模拟通过添加盐类、混浊物等因素增大声吸收系数；在α＝0.13dB／km条件下，自导作用距离为r1，在声吸收系数为α2的条件下，其自导作用半径应满足

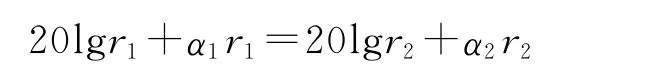
由鱼雷捕捉目标概率公式知其捕捉概率受自导半径影响，自导半径变化对目标捕捉概率情况如图1所示。

由前文论述知，仿真声吸收系数对捕捉概率影响应保持传播损失不变，假设α1为0.13，改变声吸收系数α2取值由0.13dB／km～10.13dB／km，初始自导作用距离分别为r＝1km，r＝2km，r＝3km，则随着吸声系数α2的变化，衰减损失的变化为图2所示。

图1 捕捉概率随自导半径变化关系

图2 自导距离衰减损失随声吸收系数和初始自导距离变化关系

由图1可知，自导半径在500m～1300m范围内对目标捕捉概率影响较大，超出该范围后影响较小。由图2可知，由于声吸收系数的改变，鱼雷自导作用距离衰减随声吸收增大而不断增大，在3dB／km处衰减速度相对降低。且自导半径越大，衰减损失越大。

5 结语

影响鱼雷捕捉目标概率的因素有很多，作战中鱼雷的实际自导距离和捕捉效果根本无法获得。本文通过仿真声吸收系数对声自导鱼雷作用距离影响，得到的结论对实际作战有有一定意义，尤其是对水下平台的防御有着较大参考价值，当作战平台受敌来袭声自导鱼雷攻击时，可以通过技术手段改变局部地区海水声吸收系数，降低其自导半径，从而达到“隐身”效果［11］。虽然文中部分数据是通过相关实验获得，但是仿真过程仍存在假定的参数，文中结论还需试验进一步验证。

［1］刘伯胜，雷家煜.水声学原理［M］.哈尔滨：哈尔滨工程大学出版社，2006：68－72.

［2］张振华.自导作用距离误差对声自导鱼雷捕获概率的影响［J］.潜艇学术研究，2012（30）：33－36.

［3］丁文强，李本江，邹侃.声自导鱼雷蛇形弹道搜索模型及捕获概率计算方法分析［J］.潜艇学术研究，2009（2）：49－56.

［4］迟凤阳.混浊水介质声吸收实验测量研究［D］.哈尔滨：哈尔滨工程大学硕士研究生论文，2009.

［5］Arnot W，Bass H，Raspet R.General formulation of thermo acoustics for stacks having arbitrarily shaped pore cross sections［J］.Journal of the Acoustical Socie－ty of America，1991，90（6）：3228－3237.

［6］Biot M Theory of propagation of elastic waves in a fluid－saturated porous solid，Ⅰ：low－frequency range［J］.Journal of the Acoustical Society of America，1955，28（2）：168－178.

［7］Biot M Theory of propagation of elastic waves in a fluid－saturated porous solid，Ⅱ：higher frequency range［J］.Journal of the Acoustical Society of America，1955，28（2）：179－191.

［8］Helmholtz H.Lehre von den Tonempfindungen［M］.Berlin：Vieweg Verlag，1877.

［9］Hovem J，Ingram G.Viscous attenuation of sound in saturated sand［J］.Journal of the Acoustical Society.

［10］Wang X I，Lu T J.Optimized acoustic properties of cellular solids［J］.Journal of the Acoustical Society of America，1999，106（2）：756－765.

［11］Lu T J，Hess A，Ashby M F.Sound absorption in metallic foams［J］.Journal of Applied Physics，1999，85（11）：7528－7539.