基于Bayes小子样理论的舰炮弹丸落点散布方差估计＊

马 康

（92941部队 葫芦岛 125001）

1 引言

为了对舰炮武器系统进行定型，必须进行定性试验，对试验结果进行分析以确定武器系统的性能指标。但以频率稳定性为出发点的经典统计理论是以大子样为分析基础，而昂贵的武器系统若进行大量的试验是难以承受的。在只能进行少量试验的前提下，经典统计理论的有效性将大为降低。在这种情况下，Bayes小子样统计理论得到了广泛的重视和发展［1～6］，并已广泛应用于舰炮武器系统试验中［7～10］。

Bayes方法综合样本信息与先验信息（包括专家意见、历史数据等）组成较完整的后验信息，在后验分布的基础上进行统计推断，为解决小样本问题提出了一系列方法。本文重点研究弹点散布方差的估计问题，提出动态修正Bayes估计模型。

2 Bayes参数统计模型

参数统计结构（X，B，｛pθ：θ∈Θ｝），其中参数θ是一个未知量，X＝（X1，…，Xn）T是其中一个样本。Bayes学派的基本观点是：任一未知量θ都可看作随机变量，具有不确定性，可用一个概率分布π（θ）去描述，这个分布称为先验分布。给定θ后，样本X＝（X1，…，Xn）T的密度函数为条件密度函数f（x｜θ）。

由Bayes公式可得：

式（1）确定的后验分布集中了样本和先验信息中有关θ的所有信息。后验分布族是Bayes参数估计及Bayes统计推断的出发点。这里，样本观测值是确定的，θ是随机的。通常记为

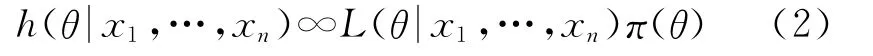
其中f（x1，…，xn｜θ）＝L（θ｜x1，…，xn）为似然函数，是定义在Θ上的θ的函数，式中“∞”表示该符号两边公差一个常数因子。式（2）可以描述多个观测值相继得到时，关于θ的信息不断更新。

当得到第一个观测值x1时，有：

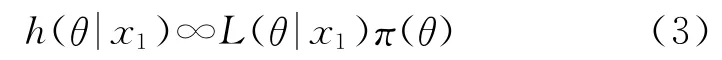
当得到第二个观测值x2时，有：

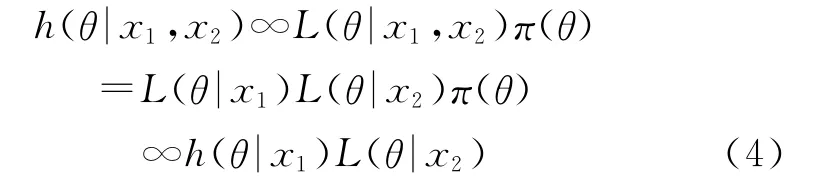
一般地，对于m＝2，…，n有：

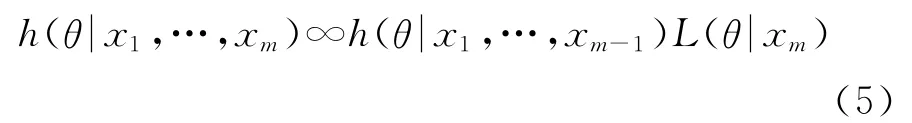
即所谓“先验”与“后验”是相对的。试验中我们不断获取新的数据信息，通过Bayes定理对后验分布进行动态修正，Bayes方法实质上描述了一个如何利用采样信息修正和改进现有的概率分布的规律。

3 弹丸落点方差的Bayes估计

3.1 基于IGamma分布的先验分布

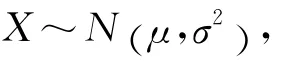
样本数据的条件密度函数为

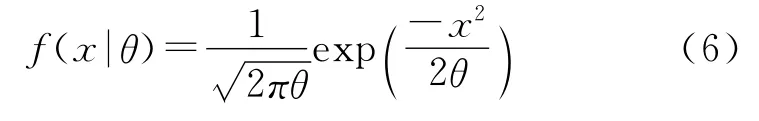
选取先验分布为IGamma分布，记为θ～IG（α，β），则有：

IGamma（α，β）分布函数的数学期望和方差分别为

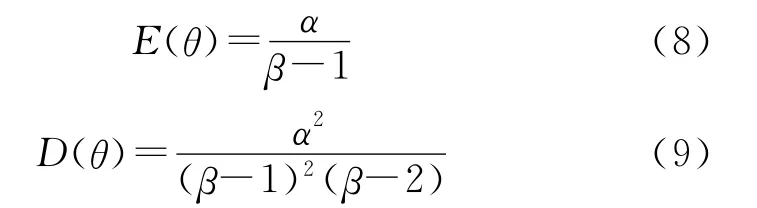
联合式（8）和式（9），可得：

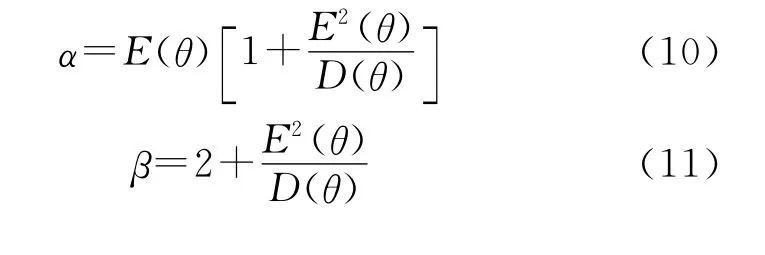
3.2 弹丸落点方差θ的估计

假设在鉴定试验之前开展了前期的研制试验，研制试验中测得m组弹丸落点数据d1，d2，…，dm，其中di为一维空间中弹点到靶心的距离。则弹丸落点的均值为

第i组弹丸的方差为

利用式（10）和式（11）可对参数α和β进行估计：

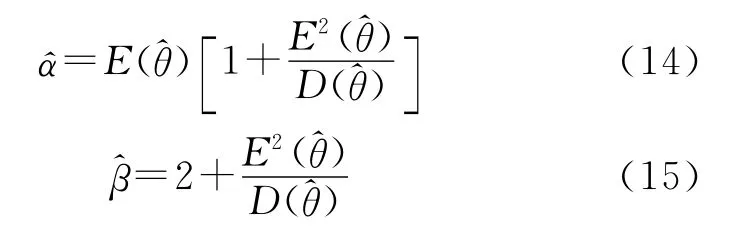
式中：

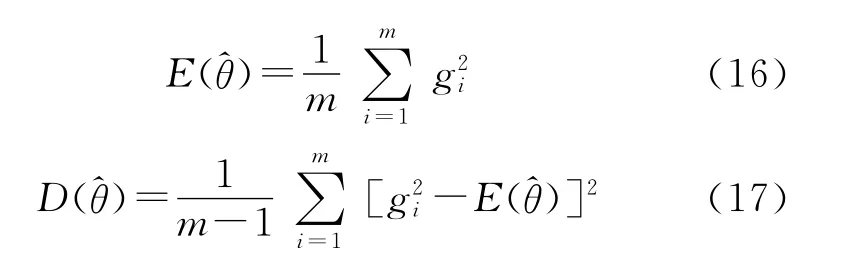
鉴定试验中，测得n组弹丸落点数据x1，x2，…，xn，由Bayes定理可得：

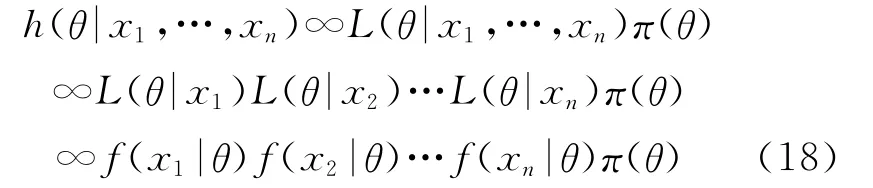
联合式（6）和式（18）可得：

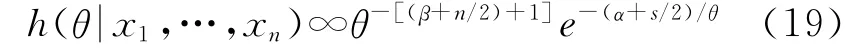
式中：

由式（19）可知，后验分布服从参数α1＝α＋s／2，β1＝β＋n／2的IG（α1，β1）分布。

对后验分布函数求数学期望得θ的Bayes估计可得：

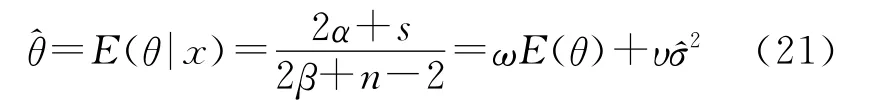
式中：

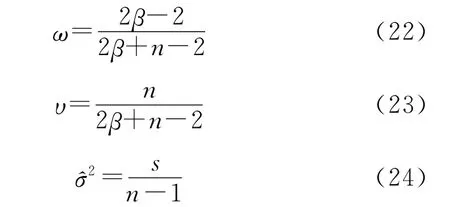
由式（21）～式（24）可知，后验均值是先验均值与样本信息的加权和，其中E（θ）为先验均值（即研制试验）为鉴定试验样本信息中θ的无偏估计，ω为先验权重，υ为后验权重。显然，ω是鉴定试验测得的样本数量n的单调递减函数，υ是鉴定试验测得的样本数量n的单调递增函数。当n较小时，先验信息占主导地位，当n逐渐增加，鉴定试验的数据信息对试验结果的评估作用逐渐增加。

4 弹丸落点方差的动态修正Bayes估计

随着武器装备研制方案的不断改进，武器试验鉴定数据也会不断更新和增加，因此，弹点散布方差的估计也是一个动态修正的过程。由式（21）～式（24）可知后验均值是先验均值与样本信息的加权和，一次次通过获得新的数据样本信息去修正原估计，由于先验信息和后验信息的相对性，每次修正得到的后验均值又可作为新的估计的先验均值。

设研制试验中弹丸落点分布（即先验分布）为θ～IG（α0，β0），则第i＋1次弹点散布方差估计的动态修正迭代为

式中，E（θi－1｜xi－1）和E（θi｜xi）分别为第i－1次和第i次弹点散布方差的Bayes估计的后验均值；为第i次样本方差的无偏估计；ωi－1为第i－1次估计时的先验权重；υi－1为第i－1次估计时的样本信息权重。

5 数值算例

5.1 先验分布的参数估计计算

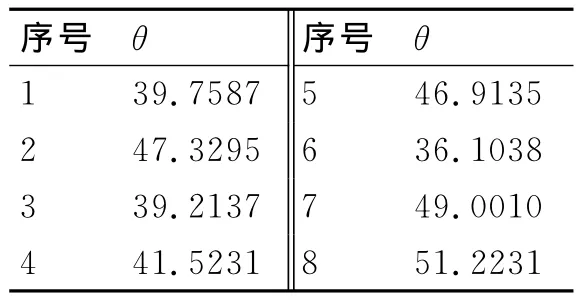
表1 模拟产生的8组随机数及其方差

5.2 先验分布的参数估计计算

由于研制试验信息服从IGamma分布，将表1的数据代入式（14）～式（17），可实现对IGamma分布的参数α和β进行估计。经计算可得：

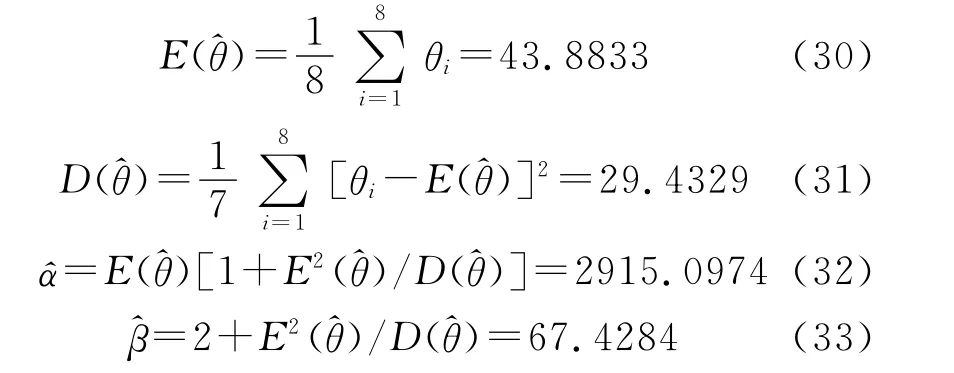
5.3 鉴定试验随机数据的生成

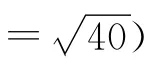
5.4 弹丸落点方差的矩估计

对表2给出的20组弹丸落点的仿真数据进行矩估计，其原理为

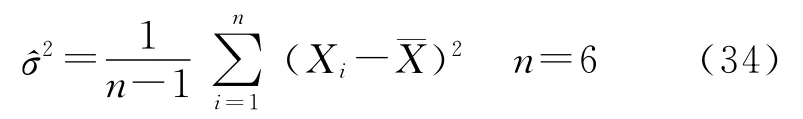
表3给出了利用矩估计法对表2中20组数据的估计值。

5.5 弹丸落点方差的动态Bayes估计

本节以表1中序号1的6组测量数据为例，给出动态Bayes估计的具体计算过程。

考虑第一个样本x1＝11.4146后，此时n＝1，弹丸落点方差的后验估计为

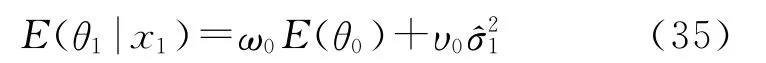
式中：

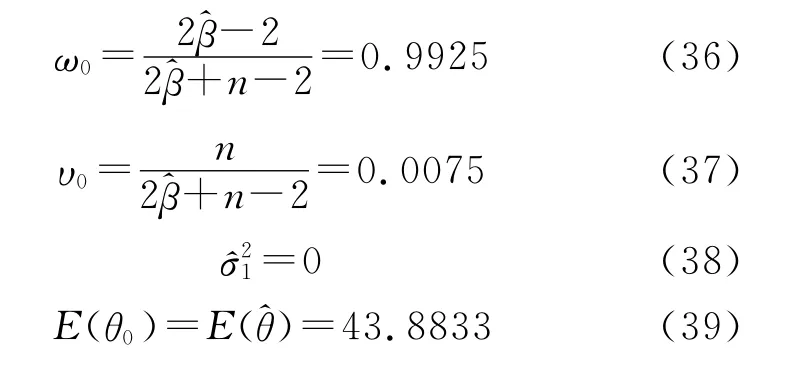
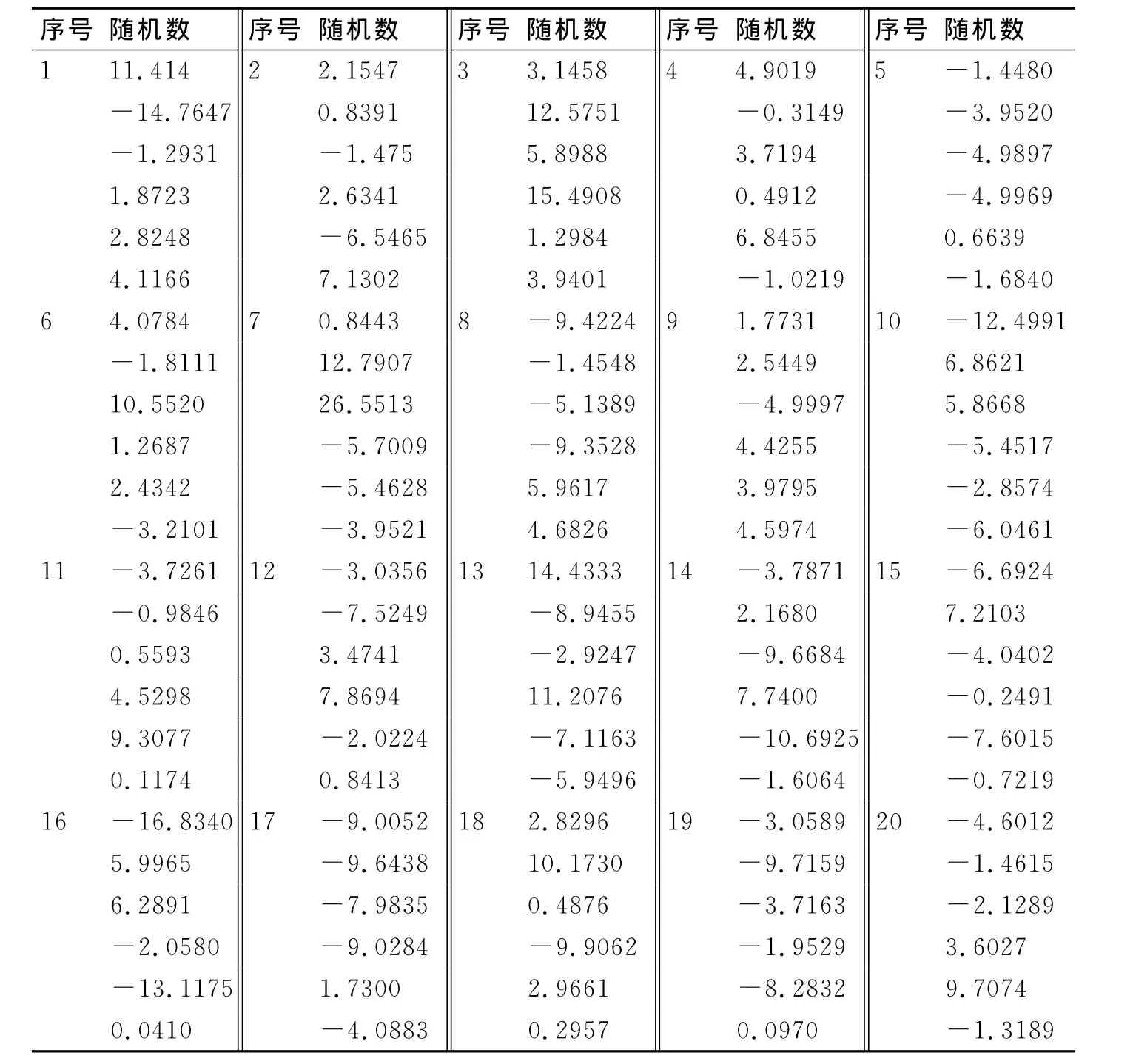
表2 模拟产生的20次测量数据

表3 20组仿真数据的矩估计方差

将式（36）～式（39）代人式（35）可求出考虑第一个测量值后的后验均值E（θ1｜x1）为

考虑第2个测量点x2＝－14.7647后，此时n＝2，弹丸落点方差的后验估计为

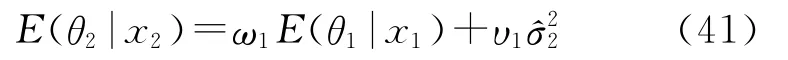
将式（42）～式（44）代人式（41）可求出考虑第一个测量值后的后验均值E（θ2｜x2）为

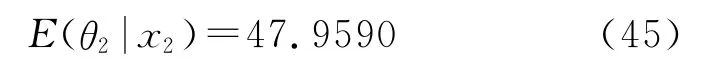
按照如上的动态Bayes估计方法对6个测量点逐一进行计算，最终可以得到考虑第6个测量点后的弹丸落点方差的后验估计为

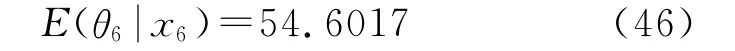
5.6 动态Bayes估计和矩估计的比较

表4给出了利用动态Bayes估计法对表2中20组数据的估计值。

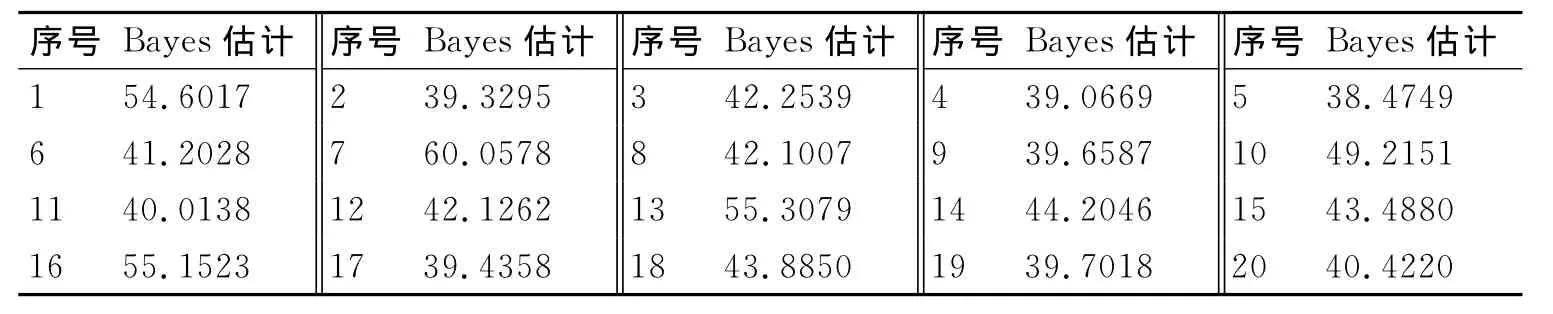
表4 20组仿真数据的Bayes估计值

图1给出了20组仿真测量点的真实均方差、传统矩估计算法结果和动态修正Bayes算法结果。由图1可以看出，动态Bayes算法明显精度高。

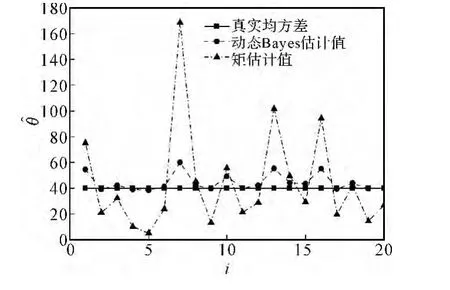
图1 动态修正Bayes算法和传统算法仿真结果

6 结语

基于后验均值是先验均值的加权和，以及样本值是在武器产品不断改进的试验鉴定过程中获得的原理，本研究采用动态修正Bayes参数估计法，利用先验信息和后验信息的相对性，将先验信息与当前样本充分结合，由迭代法求得后验均值作为参数估计，解决了由于小样本而导致的用传统矩估计法无法给出有效评估的问题。本文进一步给出了数值算例，结果表明，相对于传统的矩估计，方差的动态修正Bayes估计明显提高了估计精度，解决了小样本带来的问题。

［1］Berger J.Statistical Decision Theory and Bayesian analysis［M］.2nd edition，New York：Springer－Verlag，1985：201－222.

［2］唐雪梅，张金槐，邵凤昌，等.武器装备小子样试验分析与评估［M］.北京：国防工业出版社，2001：12－14.

［3］Sanford A D，Martin G M.Simulation－based Bayesian estimation of an affine term structure model［J］.Computational Statistics and Data Analysis，2005，49（2）：527－554.

［4］蔡洪，张士峰.Bayes试验分析与评估［M］.长沙：国防科技大学出版社，2004：73－77.

［5］张金槐，刘琦，冯静.Bayes试验分析方法［M］.长沙：国防科技大学出版社，2007：6－9.

［6］Zellner A.Information processing and Bayesian analysis［J］.Journal of Econometrics，2002，107：41－50.

［7］黄守训，王立红，田颖，等.舰炮武器系统试验与鉴定［M］.北京：国防工业出版社，2005：22－29.

［8］郑锦，武翰文.Bayes序贯决策法在舰炮武器系统试验中的应用［J］.计算机与数字工程，2009，37（8）：169－172.

［9］刘奎永，黄守训，郝瑞云.序贯分析法在舰炮武器试验中的应用［J］.火力与指挥控制，2004，29（1）：98－102.

［10］尹江丽，侯妍.数理统计方法在弹道一致性评定中的应用研究［J］.兵工自动化，2010，29（2）：30－33.