关于内外压力对油井管柱稳定性影响问题的再讨论

韩志勇

（中国石油大学（华东）石油工程学院，山东青岛266580）

李子丰教授在文献[1］中通过论证和推导，得出的结论可分为2部分：第一部分针对传统理论，认为Woods模型“与井下管柱情况不符”，“传统的油井管柱稳定拉力或虚构拉力的计算公式是错误的”；第二部分是关于内外压力对油井管柱的稳定性是否有影响，论文得出“内外压力对悬挂油井管柱的稳定性没有影响；内外压力本身对两端固定油井管柱的稳定性没有影响；两端固定后内外压力的变化对油井管柱的稳定性有影响”。2013年，文献[1］的主要内容和观点又发表在国外的一家网络杂志上[3］。文献[1］的研究结论受到某些学者的高度评价并经过网络媒体的大力宣传[4］，在社会上产生较大的影响，但其结论是否正确学术界还有不同的看法，所以有必要对文献[1］的结论进行深入地分析和讨论。

文献[1］第一部分结论，对传统理论的否定，文献[2］已经进行了详细的分析和讨论，得出结论认为，文献[1］对虚力、Woods模型、传统油井管柱稳定性的判别方法和判别公式的否定，都是不正确的，都是站不住脚的。

本文将对文献[1］的第二部分结论进行认真地分析和讨论。

1 关于自由悬挂管柱结论的讨论

文献[1］的结论说“内外压力对悬挂油井管柱的稳定性没有影响”。而且还强调说：“自由悬挂的管柱上，无论加多大的内压，只要材料不屈服，管柱就只会伸长和变粗，而不会屈曲。”；“同样，无论外压力如何变化，管柱也不会屈曲”。

这些结论是正确的吗？否！这是一个似是而非的结论。事实上，对于自由悬挂管柱来说，内外压力对其稳定性是有影响的。在不同的液压环境下，这种影响是有区别的。下面举例说明。

1.1 管外为液柱压力，管内为非梯度压力

所谓非梯度压力，是指各处的压力均相等。当管内充满气体时，气体的密度可以忽略，即可看作是非梯度压力。管外为液柱压力，管内为非梯度压力的情况在钻井中是可能遇到的。如在下套管的过程中，管内没有及时灌浆，管内即为非梯度压力。关于非梯度压力，文献[5］中有详细的论述。

图1（a）所示是管外为液体压力，管内为非梯度压力的悬挂管柱；选定x坐标的原点和方向如图1（b）所示。

管柱所受外力有管柱的重力、管柱下端面上的液压力和管内外壁上的液压力。这些外力在管柱的任意断面引起的轴向内力的计算公式分别为：

有效轴向力等于所有真实轴向力与虚力之和，即Fe＝Fa＋Fd＋Fx，则：

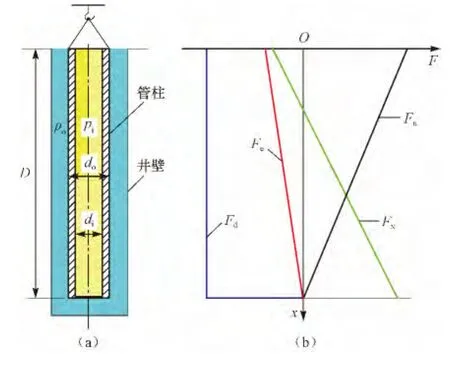
图1 管外液柱压力管内非梯度压力Fig.1 Liquid column pressure outside the string and non-gradient pressure inside the string

式中：Fa为管柱重力引起的真实轴向力，kN；Fd为管柱下端面液压力引起的真实轴向力，kN；Fx为管内外壁上液压力引起的虚力，kN；Fe为有效轴向力，kN；Ai，Ao和A分别为管柱截面的内圆面积、外圆面积和截面积，m2；D为管柱长度，m；ρs和ρo分别为管柱钢材密度和管外液体密度，kg／L；pi为管内充满气体时的压力，kPa；g为重力加速度，m／s2。

各轴向内力沿管柱轴向的变化，如图1（b）所示。整个管柱最下端的有效轴向力等于零（最大值），井口处轴向压力最大（最小值）。整个管柱都处在不稳定状态。而且，不管内压pi多大，这个不稳定状态都不会变化。这种情况下，管柱的屈曲将从上端开始发生。鲁宾斯基在文献[7］中曾论述过这种情况，并给出了具体算例。

该算例充分证明，文献[1］关于“内外压力对悬挂油井管柱的稳定性没有影响”和“无论加多大内压”，“无论外压如何变化”，“都不会屈曲”的结论是不正确的。

1.2 管内外液体密度特别高

管内外液体密度特别高，甚至比管柱钢材的密度还要高的情况在实际钻井过程中是不存在的，但在实验室可以实现。例如，在实验室把水银（其密度可达到13.595kg／L）注入管内外，就可以模拟这种液压环境。图2（a）所示为下端开口的悬挂管柱，管内外充满密度大于钢材密度的液体。该情况下，任意断面上有效轴向力的计算公式为：

式中，ρy为液体密度，kg／L。

图2 液体密度特别大的情况Fig.2 Case with extremely high density of liquid

该特例对于正常油井工程来说，虽没有实际意义，但具有重要的理论意义。对于悬挂管柱来说，内外液压力对其稳定性的影响是始终存在的。从管柱的稳定状态到不稳定状态，其间有个变化过程。随着液体密度的增大，有效轴向力随之减小，但只要还大于零，管柱就仍然处在稳定状态。当液体密度继续增大，有效轴向力继续减小，直至有效轴向力等于零，这就是临界点。如果液体密度再继续增大，有效轴向力将会小于零，整个管柱将处于不稳定状态。可见，管柱的稳定性随液体密度（也就是液体压力）的变化，是一个从量变到质变的过程。

所以，文献[1］所说的“内外压力对悬挂油井管柱的稳定性没有影响”，在理论上是不正确的。

1.3 正常钻井条件下

在正常钻井条件下，管内外充满液体，管外密度稍大于管内密度，而且都小于钢材密度。这是最常见的自由悬挂管柱，如图3（a）所示。

图3 正常钻井条件下的液柱压力Fig.3 Liquid column pressure in normal drilling conditions

管柱所受外力有管柱的重力、管柱下端面上的液压力和管内外壁上的液压力。这些外力在管柱任意断面引起的轴向内力的计算公式为：

式中，ρi为管内液体密度，kg／L。

在正常钻井条件下，ρo和ρi总是远远小于ρs。所以这个浮力系数总是大于零的。也就是说，管柱上任意断面的有效轴向力不会小于零。所以，正常钻井条件下，内外压力是不会导致自由悬挂管柱失稳的。但是，这并不等于“内外压力对自由悬挂管柱的稳定性没有影响”。参看图3（b），当存在内外液压力时，管柱的有效轴向力等于Fe；而当不存在内外液压力时，管柱的有效轴向力则与Fa相等；显然，Fe＜Fa。在内外液压力作用下，有效轴向力变小了，就等于管柱的稳定性下降了。稳定性下降了，就是受到影响了，只不过还没有降至使管柱失稳的程度。“是否失稳”与“是否有影响”不是同一个概念。所以，即使在正常钻井条件下，文献[1］的结论也是不正确的。

1.4 管内外都是非梯度压力

管内外都不存在液体压力，都是充满气体压力。这种情况在实际钻井中是很难遇到的，即使在气体钻井工况下，也很难看作是完全的非梯度压力。管内外都是非梯度压力情况下的轴向内力计算公式为：

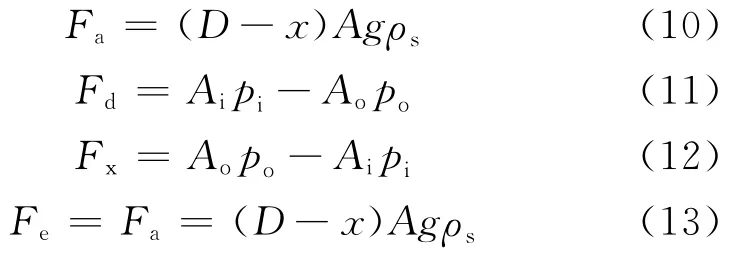
由式（13）可见，有效轴向力不受内外压力的影响。所以，对于悬挂管柱来说，只有在管内外没有液体压力即非梯度压力的情况下（见图4），才可以说“内外压力对悬挂油井管柱的稳定性没有影响”。

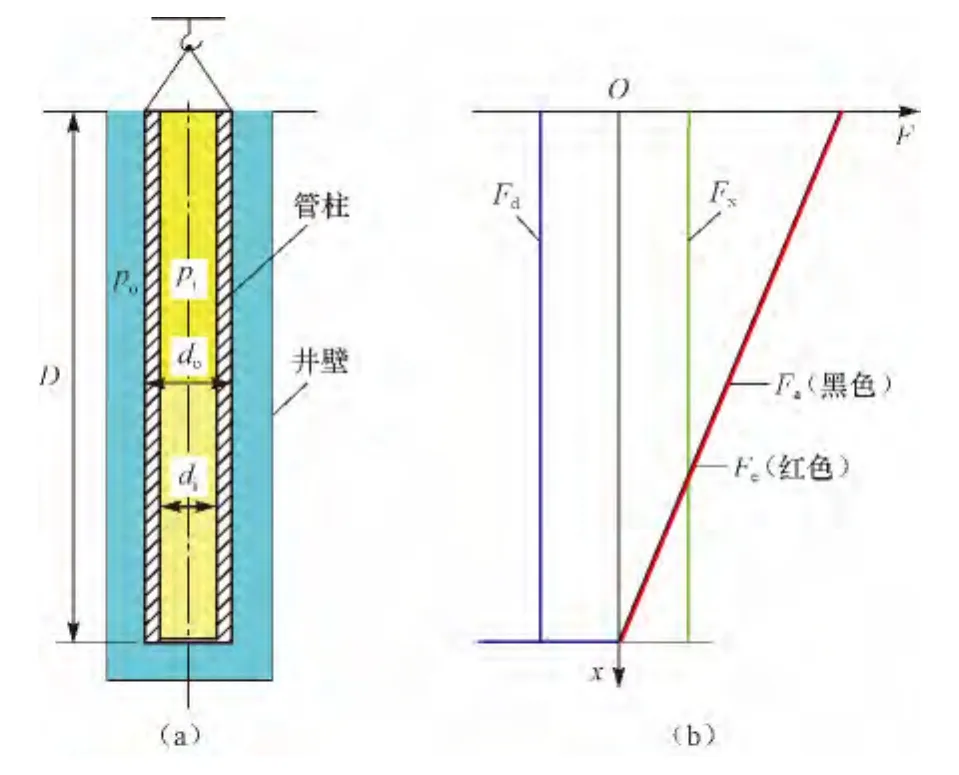
图4 管内外都是非梯度压力Fig.4 Non-gradient pressure both inside and outside the string

在液体中的管柱也可能受到非梯度压力，但不是自由悬挂管柱，而是处于水平状态的管柱。如图5所示，两端开口的自由管柱以水平状态处在液体中。这种情况下，沿管柱轴向的液体压力是没有梯度的。管柱重力与轴向垂直，所以在轴向引起的真实轴向力Fa＝0。由于沿管柱轴向的压力梯度为零，两端面液压力引起的真实轴向力Fd＝-ADgρy。管柱内外壁上液压力引起的虚力Fx＝ADgρy。则管柱任意断面上的有效轴向力Fe＝Fa＋Fd＋Fx＝0。所以，这种情况下，无论液体压力多大，管柱都不会发生失稳屈曲。

根据上述4种情况的分析可以得出如下认识：

1）管内外压力可分为梯度压力和非梯度压力。梯度压力包括沿管柱轴向的液柱压力，循环流动压力等。气体压力可看作非梯度压力，水平状态管柱沿轴向的液体压力也属于非梯度压力。

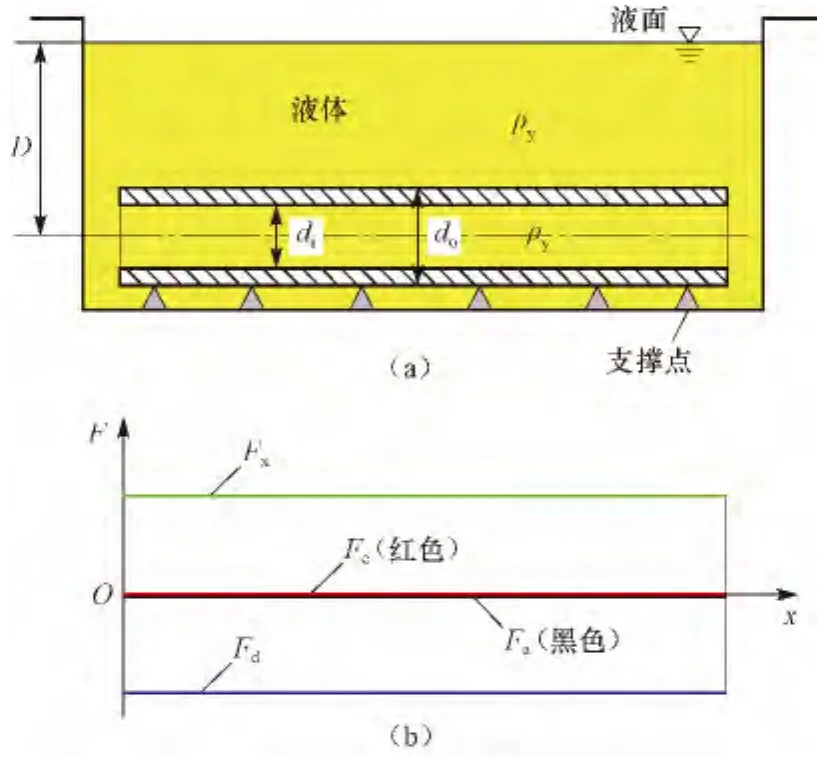
图5 处于水平状态的管柱Fig.5 String in horizontal status

2）对于自由悬挂管柱来说，管内外液体压力（液柱压力）对其稳定性是有影响的。这种影响随着液体密度的变化而变化。当液体密度小于钢材密度时，管内外压力不可能引起管柱失稳。当液体密度大于钢材密度时，管柱将处于失稳状态。

3）管外为液体压力、管内为非梯度压力的自由悬挂管柱，在管外液体密度达到一定程度（虽然远小于钢材密度）时，也会出现失稳屈曲。

4）非梯度压力对自由悬挂管柱的稳定性没有影响。

5）文献[1］关于自由悬挂管柱的结论，仅仅对非梯度压力是正确的。当管外或管内外为液体压力时，文献[1］的结论是错误的。

2 关于两端固定管柱结论的讨论

关于两端固定管柱，文献[1］说：“内外压力本身对两端固定油井管柱的稳定性没有影响；两端固定后内外压力的变化对油井管柱的稳定性有影响”。这是一个自相矛盾的结论，他把“内外压力本身”与“内外压力的变化”对立起来。

首先，从事物的一般关系来讲，如果说甲事物对乙事物有影响，那么甲事物的变量也必然对乙事物有影响；反过来说，甲事物的变量对乙事物有影响，就是承认甲事物本身对乙事物有影响。因为事物都是会变化的，事物的变化是事物本身的属性。

举例来说：核辐射对人体健康有影响，就是说核辐射的变化对人体健康有影响。或者说，核辐射的变化对人体健康有影响，就是承认核辐射本身对人体健康有影响。我们不可能说“核辐射的变化对人体健康是有影响的，而核辐射本身对人体健康没有影响”。这样说在逻辑上是不通的。

其次，文献[1］所说的“压力本身”概念不清楚。如果“压力本身”指的是两端固定管柱内外压力变化前的pi1和po1，那么，内外压力变化之后的pi2和po2是不是也属于“压力本身”呢？因为当内外压力再次由pi2和po2变为pi3和po3时，pi2和po2显然就是变化前的内外压力了！变化前后的“压力本身”对管柱的稳定性都没有影响，那么前后“压力本身”之间的差值（即变化量）对稳定性的影响又是从哪里来的呢？这不是无本之木，无源之水吗？

再次，还可以这样来分析：如果说“内外压力本身对两端固定油井管柱的稳定性没有影响”，那就相当于说：“两端固定的油井管柱内，有液压力和没有液压力，管柱的稳定性都不会变化，因为液压力对管柱的稳定性没有影响”。这就恰恰否定了第二句话——“内外压力变化对两端固定管柱的稳定性有影响”。因为“没有液压力”与“有液压力”之间，就是“压力的变化”。先说这种“变化”没有影响，接着又说这种“变化”有影响，这不是自相矛盾吗？

所以，文献[1］的结论是自相矛盾的，是不正确的。

文献[1］为什么会得出这个错误结论呢？问题出在文献[1］中公式的推导过程。

对比文献[1］关于自由悬挂管柱（图6（a））和两端固定管柱（图6（b））稳定性的论述可见，自由悬挂管柱的管端有压力，而两端固定管柱的管端没有压力，但在计算“等效轴向力”时，都按没有压力来处理，都等于下端的“真实轴向拉力”。关于两端固定管柱的稳定性，是从自由悬挂管柱的稳定性“类比”过来的。所以得出了与自由悬挂管柱相同的结论。

图6 文献[1］推导公式用图Fig.6 Figure used in Reference[1］to derive the formula

前述部分已经证明了文献[1］关于自由悬挂管柱稳定性的结论是错误的，所以，从该结论类比过来的结论也当然是错误的。可是，在计算两端固定管柱内外压力变化时的“等效轴向力”时，文献[1］又按照下端面上有液压力来计算，于是得出了自相矛盾的结论。

3 如何评价文献[1］推导的公式？

文献[1］在否定传统理论之后，根据自己的所谓“真实模型”，经过理论推导给出了一个判别管柱稳定性的公式（详见文献[1］中的式（6））：

根据该式，文献[1］得出管内外压力的变化对两端固定油井管柱稳定性的影响规律：“内压增加降低管柱的稳定性，外压增加提高管柱的稳定性。”应该说，这个规律是正确的，但这并非文献[1］的新发现，传统理论早就得出了相关规律[7，9-10］。得出正确的规律，并不能证明文献[1］中公式的推导过程正确，也不能证明该公式就具有理论意义和实用价值。

3.1 公式推导有严重错误

文献[1］推导公式所用的模型见图6。文献[2］曾指出，文献[1］的推导过程中有重大漏洞，在计算图6（a）和图6（b）2个模型的等效轴向力时都没有考虑下端面上的液压力。可是，很奇怪，在推导两端固定管柱内外压力变化时的“等效轴向力”计算公式时，明明下端面上没有液压力，文献[1］却在下端面上无中生有地加上了液压力。

对于图6（b）和图6（c）的两端固定管柱，文献[1］使用与自由悬挂管柱轴向应力相同的计算公式，这显然是不正确的。因为两端固定管柱的下端已经被水泥石固死，管内外的液压力不可能作用上去。文献[1］的做法表明，他认为管柱下端封固之后，仍然有管内外液压力的作用。这是无中生有的严重错误。

文献[1］理论推导中的严重错误表明，该文推导出的公式在理论上是站不住脚的。由于推导原理是不正确的，所以其推导的公式不具有理论意义。

3.2 文献[1］判别式的使用有很大局限性

首先，文献[1］判别式仅仅适用于判别管柱最下端的稳定性。

该公式计算的仅仅是管柱最下端的“等效轴向力”，不能用于计算管柱其他断面处的“等效轴向力”，所以只能判别管柱最下端处的稳定性，不能用于判别管柱其他断面处的稳定性。

人们常见的管柱失稳屈曲，多是从管柱下端开始。只要下端稳定，全段就一定稳定。但是在一定条件下，管柱的失稳屈曲也会从上端首先出现，上述的1.1和1.2就讲述了自由悬挂管柱从上端开始出现失稳的例子。鲁宾斯基先生早在20世纪50年代就论述过两端固定管柱从上端开始出现失稳屈曲的情况[7］，不仅给出了出现这种情况的条件，而且给出了详细的计算公式。

所以判别管柱的稳定性，不能仅仅判别管柱下端的稳定性，还应能判别管柱任意断面处的稳定性。要做到这一点，就需要计算管柱任意断面上的有效轴向力，但文献[1］中的公式计算不了。

其次，该判别式仅仅适用于管内外都是非梯度压力的情况。

如图6所示，文献[1］给出的油井管柱模型，管内外压力都是非梯度压力，即压力处处相等。但绝大多数油井管柱内外都是液柱压力，而液柱压力是梯度压力。梯度压力与非梯度压力对管柱稳定性的影响是有很大区别的。

传统理论可以方便地计算管柱任意断面上的有效轴向力，可以判别任意断面处的稳定性。传统理论既可用于梯度压力，也可用于非梯度压力，以及梯度压力与非梯度压力的组合。

文献[1］中公式的局限性表明，其实用价值有限，更不可能取代传统理论。

3.3 文献[1］严重错误的根源

文献[1］在公式推导中出现严重错误的根本原因在于文献[1］不承认虚力的存在。是否承认虚力，这是传统理论与文献[1］之间的根本分歧。为了说明这点，对文献[1］中的式（6）（即本文中的式（14））进行分析和讨论。

式（15）等号右边的第1项是文献[1］施加在管柱下端的“真实轴向拉力”。文献[2］已经指出了该“真实轴向拉力”存在的问题。本文不再讨论。

等号右边第3项-2μ（ΔpoAo-ΔpiAi）可以这样来理解：管内外压力的增量Δpi和Δpo在管柱断面上引起径向应力和周向应力的增量Δσr和Δσt；Δσr和Δσt具有引起管柱轴向应变（该应变与材料的泊松比有关）的趋势；但由于管柱两端固定不可能出现轴向应变，于是该轴向应变趋势转换为轴向力。这个轴向力姑且称为“应变转换的轴向力”。从“应变转换轴向力”的表达式可以得出：“内压增大将增大管柱稳定性，外压增大将降低管柱的稳定性”。

第2项ΔpoAo-ΔpiAi乃是传统理论所说的虚力增量，即管内外压力增量在管柱断面上引起的虚力增量。从该虚力增量表达式可以得出：“内压增大将降低管柱的稳定性，外压增大将增大管柱的稳定性”。

由于第2项总是大于第3项，所以最后的规律仍然是：“内压增大将降低管柱的稳定性，外压增大将增大管柱的稳定性”。

显然，公式中如果没有第二项虚力增量，文献[1］将会得出完全相反的规律。既然文献[1］不承认虚力，为什么会在式（14）中出现虚力增量这一项呢？这里的秘密在于文献[1］有3点做法：其一，文献[1］在两端固定管柱的下端面上无中生有地加上内外压力，并在公式推导中计算轴向力时计算了这个内外压力的增量；其二，文献[1］仅仅计算下端面处的“等效轴向力”，而下端面处的虚力增量正好与下端面上内外压力的增量大小相等、方向相反；其三，文献[1］定义的“等效轴向力”是外力，并非断面上的内力，在它给出平衡方程式（见文献[1］中的式（5））后，最后计算“等效轴向力”时需要移项，结果使这个液压力增量与虚力增量正好完全相等。正是这3点错误做法的巧合，才在公式中有了虚力增量这一项，才得出了“正确的变化规律”。

不承认虚力，就必然要用错误的做法推导公式。如果不用错误的做法，就必然得出错误的结论。这就是文献[1］的处境。

在计算自由悬挂管柱的“等效轴向力”时，明明管柱下端面上有液压力，文献[1］却故意视而不见，不予计算。在计算两端固定管柱的“等效轴向力”时，明明管柱下端面上没有液压力，文献[1］却故意无中生有地加上这个液压力。文献[1］这种不实事求是的态度是不可取的。

4 结 论

1）非梯度压力对自由悬挂管柱的稳定性没有影响。液柱压力对自由悬挂管柱的稳定性是有影响的。当液体密度小于管材密度时，管柱不会出现失稳屈曲。当液体密度大于管材密度时，管柱处于失稳状态，屈曲将首先从上端开始。当管内为非梯度压力，管外为液体压力时，自由悬挂管柱也有可能失稳屈曲。文献[1］关于内外压力对自由悬挂管柱没有影响的结论，仅仅适用于非梯度压力条件，而对液体压力以及液体压力与非梯度压力组合的情况，都是不正确的。

2）文献[1］关于“内外压力本身对两端固定管柱的稳定性没有影响，内外压力的变化对两端固定管柱的稳定性有影响”的结论，自相矛盾，不合逻辑。管内外压力及其增量都对两端固定管柱的稳定性有影响。

3）文献[1］给出的判别管柱稳定性的公式，在推导过程中有严重错误，而且仅仅适用于非梯度压力条件，只能判别管柱最下端处的稳定性。所以该公式不具有理论意义和实用价值，更不能取代传统理论中管柱稳定性的判别公式。

4）文献[1］对自由悬挂管柱下端面上的液压力视而不见，当作没有压力；而对两端固定管柱下端没有液压力，却无中生有地看作有压力。出现这些错误的根源在于它不承认虚力的存在。文献[1］如果不犯这些错误，就必然要承认虚力，否则就会得出完全相反的错误结论。

[1]李子丰.内外压力对油井管柱等效轴向力及稳定性的影响[J］.中国石油大学学报：自然科学版，2011，35（1）：65-67.Li Zifeng.Influence of internal and external pressures on equivlent axis force and stability of pipe string in oil wells[J］.Journal of China University of Petroleum：Edition of Natural Science，2011，35（1）：65-67.

[2]韩志勇.关于内外压力对油井管柱轴向力和稳定性影响问题的讨论[J］.石油钻探技术，2013，41（6）：12-18.Han Zhiyong.Discussion on effects of internal and external pressure on axial force and stability of pipe string in oil wells[J］.Petroleum Drilling Techniques，2013，41（6）：12-18.

[3]Li Zifeng.Using the fictitious force to judge the stability of pipe string is wrong[J／OL］.The Open Petroleum Engineering Journal，2013，6：57-60.[2014-04-15］.http：∥www.benthamscience／open／topej／articles／V006／57TOPEJ.pdf.

[4]潘峰.创新油气井杆管柱力学理论体系研究[N］.中国科学报，2014-01-01（21）.Pan Feng.Research of innovational theoretical system of tubular string mechanics in oil and gas wells[N］.China Science，2014-01-01（21）.

[5]韩志勇.液压环境下的油井管柱力学[M］.北京：石油工业出版社，2011：202-210.Han Zhiyong.Mechanics of tubular string in oil wells subjected hydraulic pressure[M］.Beijing：Petroleum Industry Press，2011：202-210.

[6]韩志勇.垂直井眼内钻柱轴向力的计算及强度校核问题研究[J］.石油钻探技术，1995，23（增刊1）：8-13.Han Zhiyong.Study on axial force calculation and strength check of drill string in vertical holes[J］.Petroleum Drilling Techniques，1995，23（supplement 1）：8-13.

[7]Lubinski A.Influence of tension and compression on straightness and buckling of tubular goods in oil wells[J］.Trans ASME，1951，31（4）：31-56.

[8]Handleman，M G.Bucking under locally hydrostatic pressure[J］.Journal of Applied Mechanics，1946，13（8）：A198-A200.

[9]Woods H B.Contribution to discussion of the paper by Klinkenberg A[J］∥Klinkenberg A.The neutral zones in drill pipe and casing and their significance in relation to bucking and collapse.Drilling ＆ Production Practice，1951：76-79.

[10]Chesney A J，Jr，Garcia J.Load and stability analysis of tubular strings[C］∥Paper No.69-PET-15presented at the ASME Petroleum Mechanical Engineering Conference.Tulsa，Okla，1969：21-25.