深孔内圆磨床闭式中心架的设计与优化分析
王均涛
深孔内圆磨床闭式中心架的设计与优化分析
王均涛
(上海机床厂有限公司 上海 200093)
设计一套用于深孔内圆磨床的中心架结构,利用Solidworks建立了三维模型装配体,并运用有限元分析软件对其结构进行了静力学和模态分析。分析结果表明,根据经验设计的闭式中心架的结构静态和动态性能较好,只是变形量超差。通过采取改变和增加筋板以及将翻砂孔的形状由方形改为圆形等措施,使中心架最大应力降低了62.8%,变形量减小了53.0%,固有频率有了小幅度地提高,中心架的综合性能得到了提高,实现了优化设计的目的。
闭式中心架 变形量 模态 结构优化
闭式中心架是深孔内圆磨床的一个重要部件,当卡盘夹持较长工件磨削时,另一端就需要用中心架托持,可以起到支承和定心的作用,从而保证磨削精度。闭式中心架的结构形式决定了本身的各种特性,包括静刚度和振动特性。若中心架结构设计不合理,就会导致其刚度不足和容易产生共振。中心架在工件重力的作用下就会产生较大的变形和受外界激励产生的振动,不能很好的起到支承和定心作用,降低了零件的加工精度。因此,对深孔内圆磨床中心架的优化研究就显得尤为重要。
随着CAE技术广泛地运用到机械设计中,产品的设计周期大大缩短,效率大幅度提高。通过有限元软件可以对设计的产品结构进行分析、优化,及时发现问题进行改进。运用有限元分析软件对设计的闭式中心架装配体进行静力学和模态分析,优化结构,提高刚性,达到了最优的设计目的。
1 结构设计
按照经验和传统的方法,设计了一套完整的闭式中心架结构,如图1、图2所示。中心架主要由上体壳、下体壳、端盖、导向销、螺母、丝杆、支撑块、T型槽螺栓、齿轮轴及压板等组成。其特点是上体壳与下体壳通过右端的销轴连接在一起,可以绕销轴开闭。当上体壳与下体壳闭合时,用螺钉、螺帽、手柄将其锁死。在上体壳的顶部中间位置和下体壳的左右两侧设有3个由六角螺钉、端盖、螺母、导向销及支承块组成的支承机构,可以通过旋转丝杆,使套筒和支承块伸出或者缩回,从而实现了支承和定心不同规格工件的功能[1]。
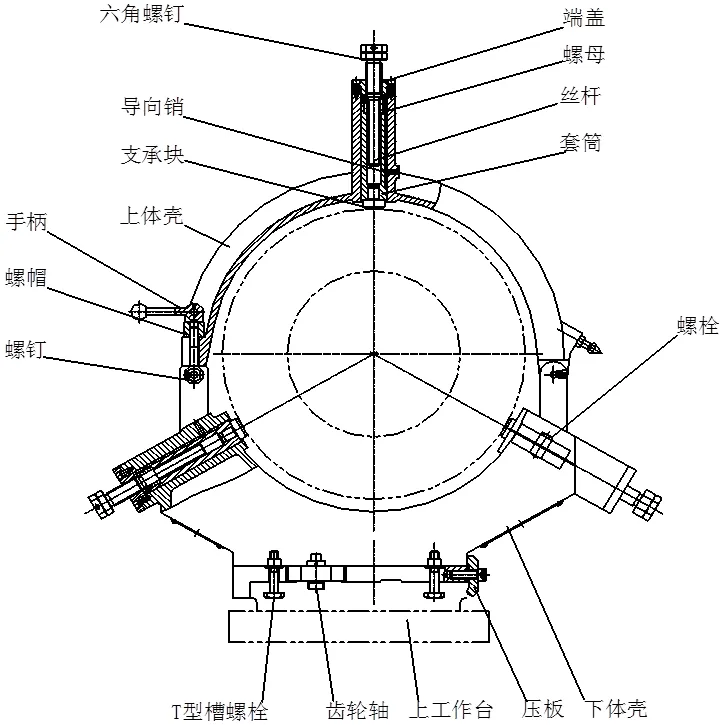
图1 中心架结构视图

图2 下体壳剖视图
2 闭式中心架的静力学分析
2.1 静力学分析理论与模型的建立
所谓静力学分析就是结构在给定静力载荷作用下的响应。因此主要关注结构的变形量、约束反力、应力以及应变等,而不考虑随时间变化的载荷、惯性和阻尼的影响[2]。其静力学方程为
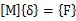
根据设计的中心架图纸,按照实际尺寸在Solidworks中建立各个零件的三维模型并进行装配,忽略小孔、凸台、螺栓等细节的影响。上体壳和下体壳的材料为灰铸铁,其它均为合金钢,相关参数见表1。
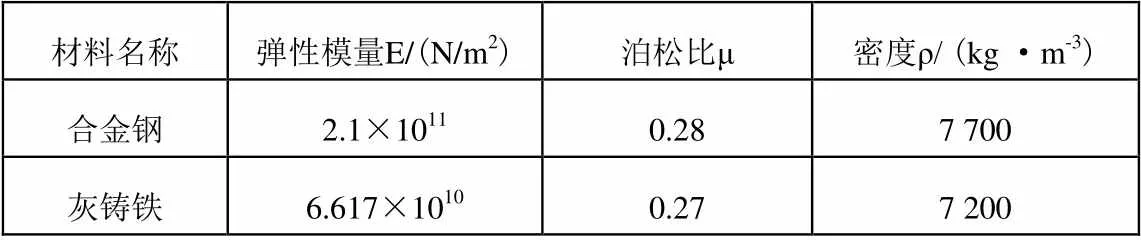
表1 所用材料属性
2.2 网格划分和接触的设置
网格的疏密程度直接影响着求解的精度和难度。单元越小,离散误差越低,但网格划分和求解时间会越长。一般情况下,可以将装配体中受力和接触的关键部位的网格细化,这样既能保证求解精度,又不会因为整个部件网格太密而导致计算费时。
选择基于曲率的网格、最大单元为58.52 mm,最小单元为11.7 mm,雅可比点位4点进行网格划分,如图3所示。

图3 闭式中心架的有限元模型
由于是装配体,零件与零件之间要进行接触设置,防止有限元分析中相互穿透,这样才能将施加的力传递给各个零件进行受力分析。接触主要有绑定、不分离、光滑无摩擦、粗糙和摩擦五种类型。前两种是线性接触,计算时仅需要迭代一次;其余三种是非线性接触,计算时需要多次迭代。因此将上体壳和下体壳之间的接触设置成摩擦,用销钉将两者固定连接;下体壳前端设置两个螺栓连接,其他零件都设置成绑定。
在系统设计时,文中设计了一个复位逻辑电路,并将微控制器的硬件逻辑归位到一个初始状态。除了上电复位,LM3S811还有软件启动的复位、看门狗定时器超时复位、外部复位管脚有效复位、输入电压过低导致的复位和LDO电压过低导致的复位等5个复位源。为了保证复位的可靠性,除了在软件部分启动了看门狗定时器超时复位之外,本设计还使用了外部复位管脚有效复位[4]。
2.3 边界条件的定义和载荷的加载
中心架通过压板固定在上工作台台面上,从而限制了X、Y、Z的自由度。通过3个圆周方向均布的支承块支承和定心工件,上体壳的支承块主要起夹紧和固定作用,工件的重力主要作用在下体壳两个夹角在120°的支承块上,最大工件重力为=1 t,由于工件一端用卡盘固定支承,因此作用在中心架上的力为1/2,受力分析如图4所示,可得
1=2=1/2=5 000 N
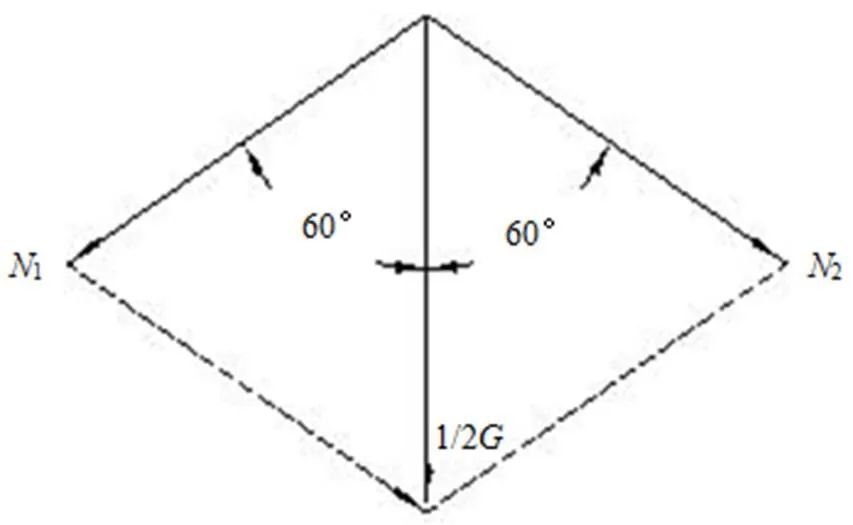
图4 闭式中心架的受力分析图
2.4 应力和变形结果
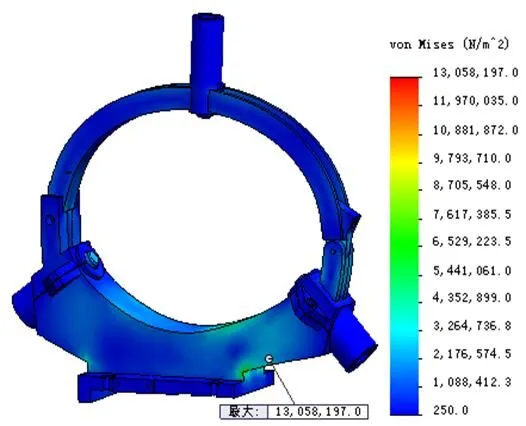
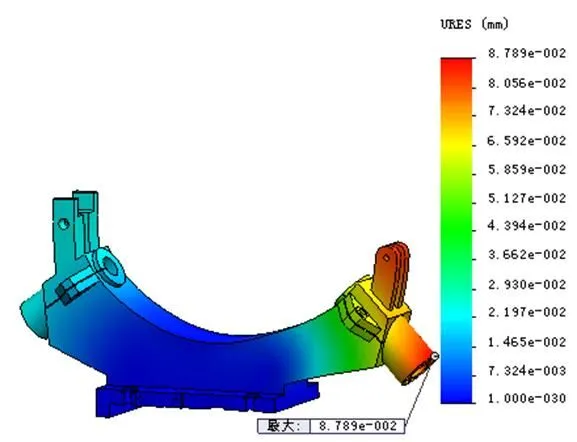
利用有限元软件对中心架装配体和下体壳进行有限元分析求解,提取计算结果,可以查看应力和变形结果,如图5(a)、(b)、(c)、(d)所示。从图5(a)、(b)图中可以看出,中心架装配体的最大应力和最大变形量分别为13.058×106N/m2、8.789×10-2mm,并且都集中在下体壳,因此有必要对其单独进行分析。图5(c)所示为下体壳的应力云图,最大应力出现在底座的结合部位,其材料为灰铸铁,最大应力远小于灰铸铁的抗拉强度(1.51×108N/m2),因此强度设计是安全的。而从图5(d)变形云图中可以看出,最大变形位置在最右端顶部,最大变形值为8.789×10-2mm,大于设计要求(5.5×10-2mm),因此,需要对下体壳设计进行优化改进。
(a)
(b)

(c)
(d)
图5 中心架装配体和下体壳的应力和变形云图
3 中心架的模态分析
模态分析是利用有限元分析的方法将多自由度系统的自由振动分解为个单自由简谐振动的叠加,或者是个固有频率振动的线性组合。
当不考虑外力和阻尼作用时,系统自由振动方程为

可求得其特征方程为
(3)
即为中心架的固有频率。从式(3)中可以看出,是一种内在属性,只与质量和刚度有关,与外界载荷无关。因此对中心架进行模态分析时,采用静力学分析时的模型,只对中心架底面进行固定约束,不施加任何载荷。由于低阶模态对振动系统的影响较大,所以对中心架的模态分析并不要求解出全部的频率和振型,而是求出几阶就可以满足分析需要,在分析软件中进行频率分析,可得到前四阶固有频率如表2,振型如图6(a)、(b)、(c)、(d)所示。
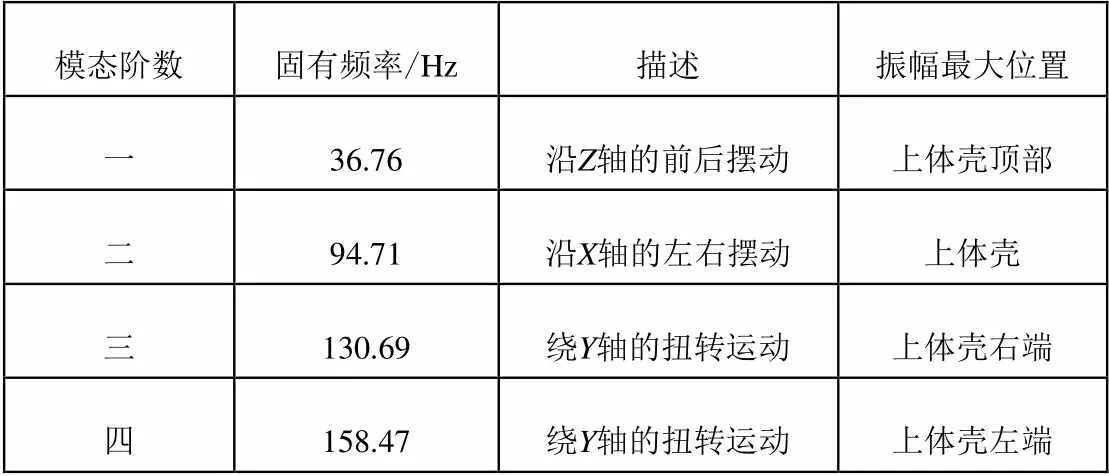
表2 中心架前四阶模态结果

(a) 一阶振型
(b) 二阶振型

(c) 三阶振型
(d) 四阶振型
图6 中心架模态振型
从表2和图6分析可知:
(1)第一、二阶为摆动振型,第三、四阶为扭曲振型;
(2)第三、四阶振型大致对称。由于模型结构和约束比较对称,从而形成了两个相近的固有频率,即式(3)中有两个大小相近的特征值,只是振型在空间上相差一个相位角度。
(3)由于床身上头架电动机的转速都为1 200 r/min,即为20 Hz,小于中心架一阶固有频率(36.76 Hz);内圆磨杆转速4 500 r/min,即为75 Hz,大于一阶固有频率36.76 Hz,但小于二阶固有频率94.71 Hz,因此不会发生共振。
从上面的分析中可以看出,由传统方法设计的中心架的静态和动态性能较好,安全系数很高,只是其静变形量大于设计要求,需进行结构优化。
4 结构的改进与优化
由于中心架的静变形量较大,因此需要对其结构进行优化。从以上的分析可知,在最大应力和最大变形量存在的下体壳部位,采取增加筋板,改变结构将翻砂孔的形状修改为圆形结构,如图7所示。由于结构的改变,导致原来的压板结构和位置不能使用,在下体壳的右端左右增加了两个凸台,不仅可以固定压板的位置,也可增强其刚性。优化前是一块压板,优化后为两块压板[3-5]。优化后的中心架结构如图8所示。

图7 优化后下体壳的结构
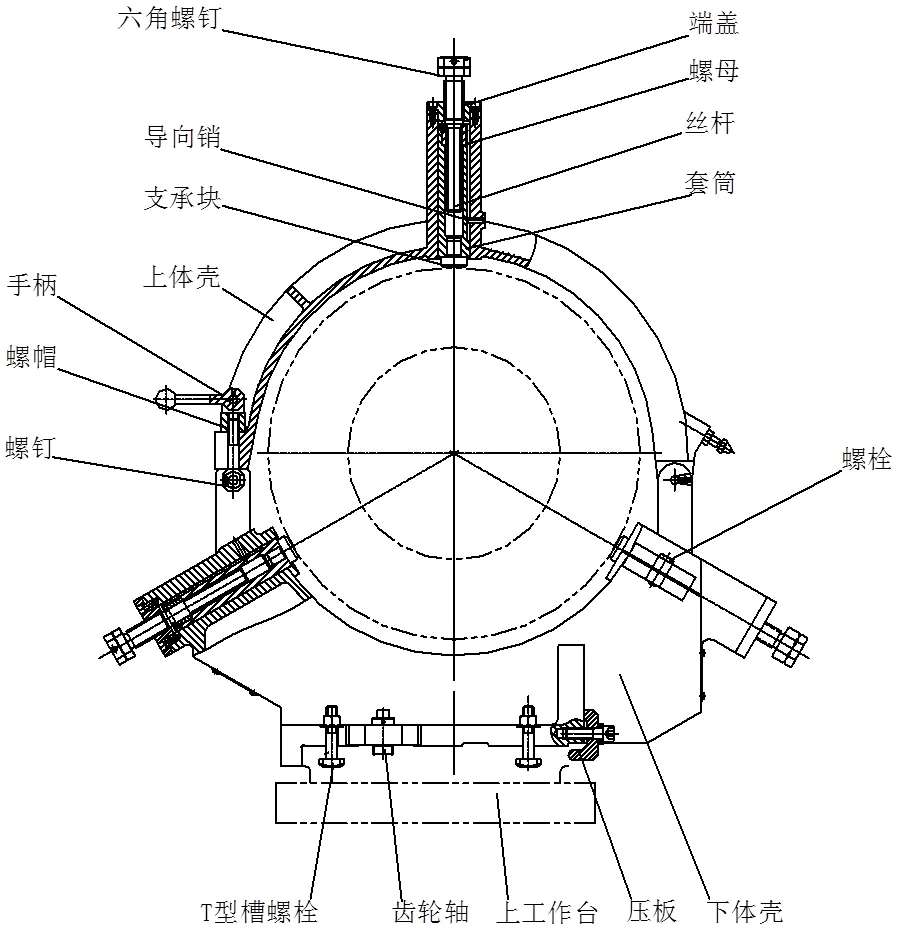
图8 优化后中心架的结构视图

(a) 一阶振型
(b) 二阶振型
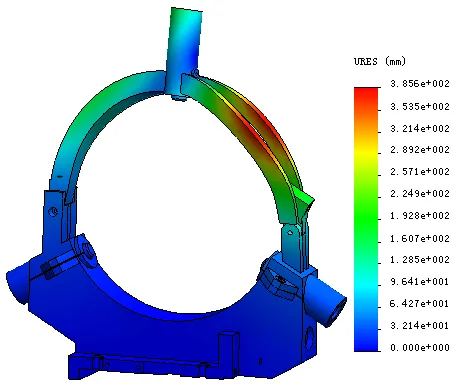
(c) 三阶振型
(d) 四阶振型
图9 优化后中心架模态振型

(a) 优化后中心架装配体应力云图
(b) 优化后中心架装配体变形云图
图10 优化后中心架应力和变形图
把优化后的中心架再次进行静力学和模态求解,前四阶的固有频率分别为37.71 Hz、104.79 Hz、142.98 Hz、160.08 Hz,各阶频率都有小幅度提高,从图9中可以看出,各阶变形相对于优化前的变化不大,部分区域变形增加也只是在局部区域,对工件的磨削精度影响很小。从图10中可以看出,优化后中心架的最大应力大幅度地减小,由13.058×106N/m2减小到了4.863×106N/m2,减小了62.8%;最大变形量由8.789×10-2mm减小到了4.131×10-2mm,减小幅度达53%。因此增加筋板,将翻砂孔更改为圆形等措施使中心架有了更好的抗弯、抗扭刚性。通过以上的优化,使中心架的性能有了很大的提高,达到了最优设计的目的。
5 结语
根据要求设计了深孔内圆磨床的中心架结构及其整套图纸。利用Solidworks建立了三维模型装配体,并在有限元分析软件中对其进行了静力学和模态分析。分析结果表明,通过经验设计的闭式中心架的静态和动态性能较好,只是变形量大于设计要求。通过采取改变和增加筋板以及将翻砂孔的形状由方形改为圆形等措施,对优化后的结构再进行有限元分析。结果表明,优化后的中心架最大应力降低了62.8%,变形量减小了53%,模态频率有了小幅度地提高,中心架的综合性能达到了最佳,达到了优化设计的目的。此中心架已经在磨削中使用,起到了很好的支承和定心作用,计算的变形量结果与现场实际测量的非常接近。
[1] 徐灏,邱宣怀,蔡春源,等.机械设计手册[M].北京:机械工业出版社,1991.
[2] 蒋孝煜.有限元法基础[M].北京:清华大学出版社,1992.
[3] 孙靖民,梁迎春,陈时锦,等.机械结构优化设计[M].哈尔滨:哈尔滨工业大学出版社,2004.
[4] 从明,房波,周资亮,等.车拉数控托板有限元分析及优化设计[J].中国机械工程,2008,19(3):207-213.
[5] 张宪栋,徐燕申,林汉元.基于FEM的数控机床结构部件静动态设计[J].机械设计,2005,22(5):29-31.

