海底隧道全断面注浆渗流场分析

郭 瑞，周晓军，王 爽，汪精河

(西南交通大学土木学院，成都 610031)

近年来我国海底隧道的建设突飞猛进。目前已建成的海底隧道有厦门翔安海底隧道和青岛胶州湾海底隧道。在海底隧道修建和运营过程中，海底隧道高承压水所带来的困难也十分突出，海底隧道具有水头相对稳定、水源充足等特点，尤其是隧道穿越破碎带、节理裂隙等渗水量大的地段，一旦隧道开挖与海水连通，海水就会成为突水的水源，易引起隧道塌方、突水、突泥等事故。在海底隧道穿越断层破碎带时，如何有效地控制和疏导隧道施工过程中所遇到的承压地下水是隧道安全施工和运营的关键所在。

在隧道施工期间采取合适的防排水措施，可以有效地降低施工风险和控制运营成本。海底隧道注浆不仅可以充填岩体裂隙、封堵地下水，从而提高围岩抗渗能力，对衬砌外水压力进行有效的折减;同时注浆后浆液固化变成岩块间的胶结材料，提高围岩摩擦角、黏聚力等力学参数，有效地提高了围岩的力学性能［1－3］。合理注浆是关系到海底隧道安全施工的关键环节。

数值模拟和解析方法是研究海底隧道渗流场问题的常用方法，近年来许多国内外学者在这方面做了大量研究，Bouvard和Pioto提出了渗流场理论;Harr采用镜像法对隧道渗流场进行了计算，并对隧道围岩空隙水压力分布进行了分析;王星华等通过建立海底隧道的等效连续介质模型，得出了隧道涌水量与隧道排水量差距越大，衬砌外水压力越大的结论［4-6］。

水工隧洞设计规范规定:地下水压力实际上是在渗流过程中渗透水作用在围岩和衬砌中的体积力，可通过渗流分析决定相应的水荷载［7］。为了准确掌握注浆圈对海底隧道渗流场作用的机理，通过建立海底隧道开挖的等效连续介质的模型，用复合式衬砌“等效渗透系数”来代替防水板和排导系统的作用［8，9］，以期进行轴对称解析解结果和数值模拟结果的对比分析，研究不同注浆圈半径和渗透系数以及不同排水方式对隧道衬砌外水压力和隧道涌水量的影响。

1 流固耦合计算原理

FLAC3D计算岩体的流固耦合效应时，多将岩石中的裂隙水流按流量等效原则抽象为等效连续介质，实际岩体中由于裂隙中的实际流速比等效连续介质的达西流速要大若干量级，因而这种等效连续介质模型只能用作模拟恒定渗流模型，不能用于非恒定渗流模型［10］。

流固耦合时流体在孔隙中的流动遵循Darcy定律，同时满足Biot方程。其优点有:可以方便设置流体边界条件;可以考虑渗流场的历史变化过程。其关键几个微分控制方程［12］如下所述。

(1)平衡方程

对于小变形而言，流体质点平衡方程为［11］

式中，qi，i是渗流速度，m/s;qv是被测体积的流体源强度，1/s;ζ是单位体积孔隙介质的流体体积变化量。

(2)运动方程

流体的运动形式用Darcy定律来表示。对于均质、各项同性固体和流体密度是常数的情况，运动方程表述为［11］

式中，k为介质的渗透系数，m/s;ρf为流体的密度;xi为3个方向上的距离梯度;gi为重力加速度的3个分量。

(3)本构方程

流体流量的改变与孔隙压力、饱和度及固体体积应变有关。孔隙介质本构方程的增量形式为［11］

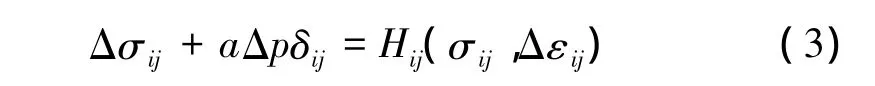
式中，Δσij为应力增量;Hij为给定函数;εij为总应变。

(4)相容方程

应变速率与速度梯度之间的关系为［11］

式中，u为介质中某点的速度。

2 隧道涌水量与衬砌外水压力的解析解

2.1 隧道的渗流模型

为分析海底隧道的渗流场，设隧道位于半无限含水层中，其四周水压为均匀分布。根据地下水力学理论，可推导出衬砌外水压力和隧道涌水量的轴对称解析解，隧道渗流场的理论计算模型如图1所示［12］。

图1 海底隧道的渗流模型

隧道衬砌的外水压力为［13］

隧道每延米的涌水量为［13］

式中，K1为衬砌等效渗透系数;K2为注浆圈渗透系数;K3为围岩渗透系数;γW为孔隙流体容重;r0为衬砌内半径;r1为衬砌外半径;r2为注浆加固圈半径;r3为注浆圈到海床的距离;P1为作用在衬砌上的外水压力;H为海平面与隧道的高差。

通常海底隧道的覆土厚度、隧道半径、衬砌渗透系数变化不大，由上述公式可知，隧道渗流场主要由围岩渗透系数、注浆圈半径和排水方式决定。

2.2 注浆圈对渗流场的影响

为分析注浆圈对隧道涌水量和衬砌外水压力的影响，根据图1建立隧道渗流模型:衬砌内半径r0=5 m，衬砌外径r1=5.6 m，r2为注浆加固圈半径，隧道中心与海平面的高差 H=70 m、孔隙流体容重 γW=10 000 N/m3，隧道控制排水量为3 m3/m·d。为研究注浆圈设计参数对渗流场的影响，对表1所列工况进行分析。

表1 孔隙水压力分析工况

将上述各个参数代入式(5)、式(6)可计算得到隧道衬砌拱底外水压力、隧道涌水量与注浆圈半径、注浆圈渗透系数的关系如图2和图3所示。

从图2、图3中可以看出:隧道采用控制全排水时，注浆圈的厚度从2 m增加到6 m，隧道涌水量和衬砌外水压力减少的并不明显，而注浆圈渗透系数的变化对衬砌的外水压力和隧道涌水量影响都较为明显。

图2 控制排水时隧道衬砌外水压力的理论值

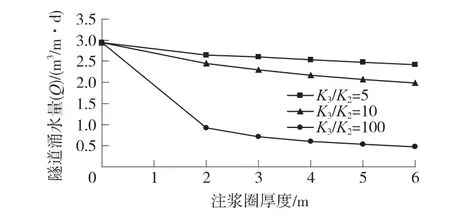
图3 控制排水时每延米隧道涌水量的理论值

3 数值模拟分析

3.1 计算模型及参数

为与轴对称解析解进行对比，建立数值模型如下:隧道位于海平面下70 m，隧道覆盖层厚25 m，隧道断面为圆形截面，半径为5 m，衬砌厚度为0.6 m，隧道控制排水量为3 m3/m·d。考虑边界效应影响，计算模型尺寸取为160 m×95 m×1 m，采用平面应变模型，如图4所示。模型共有6 560个单元、13 374个节点。物理模型为mohr-coulomb弹塑性模型，模型前后、左右及底部边界为固定边界，上表面为自由边界;流体模型为等效连续介质模型，围岩前后、左右及底部边界为不透水边界，上表面为透水边界，开挖边界为透水边界、固定孔压为0。

图4 计算区域及单元网格

隧道穿越破碎带，基岩为弱风化岩层。采用强度等效原则，提高隧道围岩的黏聚力和摩擦角代替锚杆在支护结构中的作用;参考铁路设计规范，将钢拱架的强度折算到喷射混凝土上。围岩及衬砌的物理力学参数见表2。

数值模拟中，注浆方式采用全断面帷幕注浆，开挖方式为全断面开挖。模型中初始地应力场只考虑自重应力场，初始孔隙水压力为静水压力分布。

表2 围岩及衬砌物理力学参数

开挖模拟时，用复合式衬砌“等效渗透系数”来代替防水板和排导系统的作用，模拟隧道的隧道控制排水工况。全封堵防水时，取衬砌等效渗透系数为0代替防水板作用。为研究注浆加固圈设计参数对隧道渗流场的影响，对表1所示工况进行流固耦合模拟分析。数值模拟时，在衬砌外圈的拱顶、拱腰及拱底设置监测点(图5)，监测隧道衬砌外水压力。

图5 衬砌水压力监测点

3.2 衬砌外水压力及涌水量分析

通过对隧道围岩与地下水耦合作用下开挖过程模拟得出:隧道开挖时隧道周边的孔隙水压力有明显的减少，地下水在洞室周围的孔隙水压力呈漏斗型分布，如图6所示(各种工况的水流矢量图类似，因此只给出工况1－1的水流矢量图);毛洞开挖时洞室边界的孔隙压力越来越小，最终趋于一个极小的稳定值;添加衬砌后，衬砌外水压力先急剧增加，经过一段时间后增速变缓，最终趋于稳定(图7)。

图6 工况1－1加衬砌后的水流矢量图

图7 工况1－1衬砌拱顶外水压力随时步变化曲线

分析衬砌外水压力和隧道涌水量时，取所有工况的衬砌外水压力达到稳定后的时步作为分析时步(图7中A点的时步)。对各种工况耦合模拟，得到的指定时步的衬砌外水压力和每延米隧道日涌水量进行分析，得出以下几点认识。

(1)分析注浆圈渗透系数为2×10－5cm/s时，隧道拱顶、拱底、拱腰衬砌外水压力，发现衬砌外水压力有如下关系:拱顶＜拱腰＜拱底。衬砌不同部位外水压力见图8。

图8 衬砌不同部位外水压力

(2)渗流场稳定后，分析封堵不排水隧道的注浆工况和不注浆工况衬砌外水压力，可以看出:全封堵防排水方式时，不论隧道是否注浆，衬砌外水压力都随时间的推移越来越大，最终衬砌的外水压力趋于稳定且等于未开挖时的静水压力(图9)，与解析解的结果一致;注浆不排水工况与不注浆时的衬砌外水压力变化趋势相同，仅渗流场稳定所需的时间步增多。因此全封堵防水方式，注浆不能改变隧道渗流场稳定后的衬砌外水压力，只能增加渗流场稳定的时间。

图9 封堵不注浆工况孔压稳定后水压力分布

(3)图10中可以看出:隧道设计考虑排水时，渗流场稳定后隧道的衬砌外水压力相对于静水压力均有不同程度的折减;本次数值模拟中，控制排水量时，当注浆圈渗透系数与围岩渗透系数比为5时，相应工况中拱腰最大衬砌外水压力为577 kPa，水压力折减系数为0.82;当注浆圈渗透系数与围岩渗透系数比为1时，拱腰最小衬砌外水压力为96.4 kPa，折减系数为0.138。可以看出控制隧道排水量时，合理的调整注浆圈渗透系数和注浆圈厚度可以有效控制隧道衬砌的外水压力。

(4)从图10、图11中可以看出:控制排水工况中，由隧道注浆圈参数引起的隧道涌水量和外水压力同步变化。当注浆圈渗透系数减少时，隧道涌水量和外水压力有着明显的减小;在注浆圈渗透系数一定的条件下，增加注浆圈的厚度，稳定后的衬砌外水压力和涌水量都有减小，但效果并不显著。因此相较于注浆圈径向变化，注浆圈渗透系数变化对渗流场的影响更为明显。

图10 拱腰衬砌外水压力与注浆厚度变化曲线

图11 隧道涌水量与注浆厚度变化曲线

(5)与理论计算的衬砌外水压力和涌水量与数值模拟的结果进行对比分析，可以看出数值模拟的涌水量和衬砌外水压力相比理论计算的结果较大，但相差不多，且二者的变化规律相同。控制排水时，理论计算所得衬砌外水压力为572.4 kPa，数值模拟所得衬砌拱腰处外水压力为577 kPa;所有工况中二者相差最大百分比为4.78%。

5 结论

基于流固耦合机理，研究了控制隧道涌水量时，注浆圈渗透系数和注浆圈厚度对衬砌外水压力和隧道涌水量的影响。主要结论如下。

(1)注浆圈渗透系数的变化对衬砌外水压力和涌水量有明显的影响，在考虑隧道排水时，注浆时适当提高注浆圈的抗渗性，可以有效地控制衬砌外水压力和隧道涌水量。而增加注浆圈厚度对于海底隧道涌水量和衬砌外水压力的降低影响效果并不明显，仅为减少隧道的涌水量而加大注浆圈的厚度是不合理的，考虑注浆圈的厚度应主要以力学加固为主、防排水为辅。

(2)注浆可以改变渗流场的分布，是海底隧道重要的施工控制措施。全封堵排水时，隧道注浆不能改变隧道衬砌最终的外水压力大小，衬砌的外水压力基本等于静水压力;控制排水时，只要衬砌地下水排导系统设计参数得当，施工质量得到保证，就基本上可以将水压力荷载消减到可以忽略的程度，并可以有效地控制隧道的涌水量。

(3)考虑到衬砌的拱底外水压力要大于拱顶外水压力，同时衬砌的拱腰到拱脚段的内力较大，因此施作隧道支护时要合理优化隧道拱底、拱腰支护结构。

(4)数值解与轴对称解析解结果相差不大，因此使用轴对称解析解分析隧道的涌水量和衬砌外水压力具有可行性。对于具有一定水头的海底隧道［14］，可以利用先由数值模拟解出隧道复合式衬砌的等效渗透系数，再由轴对称解析解的方法分析隧道的排水量和衬砌外水压力。

(5)研究只考虑了隧道注浆对渗流场的影响，未考虑注浆对围岩应力场的影响。实际注浆时浆液凝固并与周围岩块的胶结加大了围岩的内摩擦角、黏聚力、弹性模量等物理属性，对改善围岩的力学性能，稳定隧道洞室起了重要的作用。实际工程中，施作注浆需根据工程地质、水文地质和洞室断面情况，同时兼顾注浆圈对渗流场和应力场的影响选用适当的注浆方案。

［1］张志强，李化云，何川.基于流固耦合的水底隧道全断面注浆力学分析［J］.铁道学报，2011(2):85-90.

［2］李地元，李夕兵，张伟，宫风强，黄炳仁.基于流固耦合理论的连拱隧道围岩稳定性分析［J］.岩石力学与工程学报，2007(5):1056-1064.

［3］徐金华，何川，夏炜洋.水下盾构隧道渗流场应力场耦合效应研究［J］.岩土力学，2009(11):3519-3527.

［4］HOUVARD M，PINTON.Amenagement Capiviari-Cachoe-ira;Etude Dupuits Encharge［J］.La Houille Blanche，1969(7):747-760.

［5］汪优，王星华，刘建华，陈俊儒.基于流固耦合的海底隧道注浆圈渗流场影响分析［J］.铁道学报，2012(11):108-114.

［6］白国良.基于FLAC3D的采动岩体等效连续介质流固耦合模型及应用［J］.采矿与安全工程学报，2010(3):106-110.

［7］高新强，仇文革.隧道衬砌外水压力计算方法研究现状与进展［J］.铁道标准设计，2004(12):84-87.

［8］郑波，王建宁，吴剑.基于等效渗透系数计算衬砌水压力方法研究［J］.现代隧道技术，2011(12):43-46.

［9］郑波.隧道衬砌水压力荷载的实用化计算研究［D］.北京:中国铁道科学研究院，2010.

［10］张有天.岩石水力学与工程［M］.北京:中国水利水电出版社2005:112-113.

［11］Itasca consulting group，Inc..FLAC3DFluid-mechanical interaction(Version2.1)［R］.［S.l.］:Itasca consulting Group，Inc.2003.

［12］关宝树.隧道工程设计要点集［M］.北京:人民交通出版社，2003:147-152.

［13］吉小明，王宇会.隧道开挖问题的水力耦合计算分析［J］.地下空间与工程学报，2005(12):848-852.

［14］张志强，何本国，何川.水底隧道饱水地层衬砌作用荷载研究［J］.岩体力学，2010(8):2445-2470.