通用强度折减点安全系数的定义及在边坡稳定分析中的应用

□王 佳（山西省水利建设开发中心）

0 引言

点安全系数是衡量结构安全度的重要指标，其计算方法主要有传统安全系数法、超载法、传统强度折减法。传统强度折减法的定义为保持作用在模型上的荷载大小与分布不变，按一定的方式逐渐降低材料强度参数值，直到模型破坏。传统强度折减点安全系数即是材料的设计强度参数和模型破坏时的材料强度参数的比值，该参数反映了材料每一点的强度储备。但是该安全系数有非常大的局限性。首先，对于某些准则，例如mohr-coulomb准则来说，传统强度折减系数有取值上的局限性——必须在一定的取值范围内才能使该方法有意义。另外，对于在确定拉压比情况下的多参数准则，不同的参数折减会造成此系数的不同结果，影响结构安全度的判断[1]。因此，定义一个不受上述限制的通用的强度折减安全系数是非常必要的。

1 基于通用强度折减法的点安全系数

1.1 通用强度折减点安全系数的定义

对于各向同性材料，材料的破坏面或强度极限面在主应力空间一般表示

或用应力不变量表达[2]如式

或用Haigh-Westergaard坐标系[3]表示为：

其中：

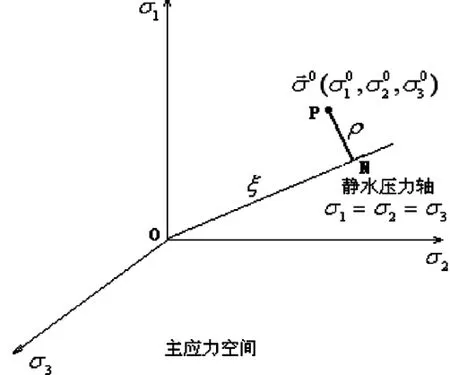
图1 主应力空间中应力状态的几何表示图

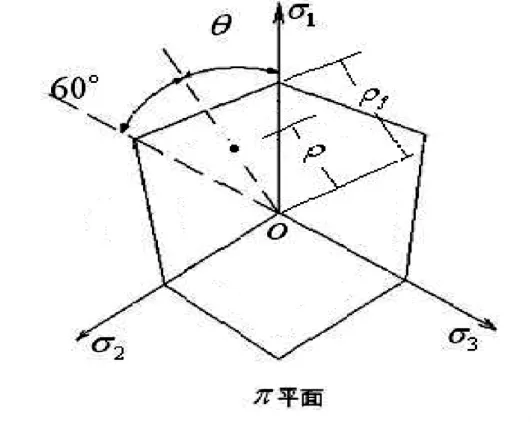
图2 极半径与临界极半径示意图

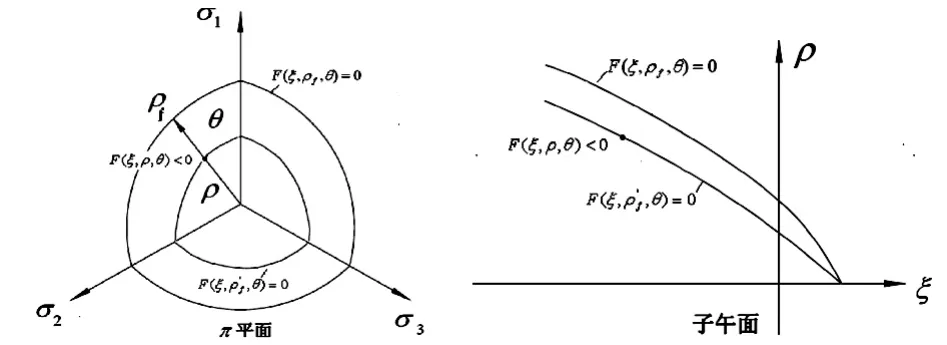
图3 通用强度折减法的物理意义图

通用强度折减法也是基于强度折减的思想，不同的是，其物理意义不是指强度参数的折减，而是通过π平面临界上极半径ρf的扩大或缩小，使强度极限面整体扩大或缩小，最终使得应力点落在强度极限面上，即达到强度极限状态，如图3所示。由此，定义新的安全系数——通用强度折减安全系数表达式为：

根据定义，可以得到新定义的安全系数满足以下条件：

图4 通用强度折减安全系数计算示意图

1.2 通用强度折减点安全系数计算

如上节所示，通用强度折减点安全系数为应力点相应的临界极半径与该点极半径的比值。临界极半径的求解如图5，以Mohr-Coulomb准则为例，E点为应力点D到强度极限面最短距离的点，也称为失效点。DE为应力点D的失效距离[3]。从图4中可以看出DE⊥AC，且△ABC≌△DEF≌△EFC，根据相似关系，可以得到

其中：

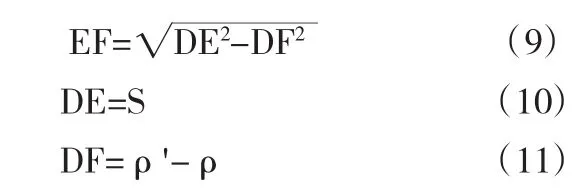
从而可以得出：

当准则的强度极限面为曲线时，求解时可以用曲线的割线距离来计算。因此可以得到该应力点的通用强度折减安全系数：

通用强度折减系数的几何意义就是调整强度极限面F(ξ,ρf,θ)＞0，使其极半径除以一个系数 Kf，从而使应力点（σ1，σ2，σ3）落在新的假设强度极限面F(ξ,ρf/Kf,θ)=0上。换言之，也即是保持其ξ,ρ,θ，也就是其应力状态不变，调整应力点σ1，σ2，σ3）的半径乘以一个系数Kf，使其落在强度极限面上，得到 F(ξ,ρ·Kf,θ)=0，以 Mohr-Coulomb 准则为例，如图 5所示。

图5 通用强度折减法的几何意义图

2 通用强度折减安全系数在水利工程中的应用

安全系数在水利工程中有大量应用，经常见于堤防边坡、大坝边坡及岩洞的稳定计算。此处以某河流堤防工程边坡稳定分析为例，通过有限元建模计算，分析比较通用强度折减安全系数与传统边坡稳定安全系数的计算成果。

2.1 工程概况

某河流边坡堤防工程全长3.52 km。该工程右岸堤防桩号0+700～3+515段按河堤标准进行护砌，采用斜坡式和直斜复合式断面，堤顶宽12.00 m，堤顶高程5.10～5.70 m。根据景观总体布局，堤顶高程5.10～高程3.50 m、高程3.50 m～高程2.50 m分别采用三维植被网、干砌方块石和直挡墙护砌，并适当布置景观台阶和观光平台，高程2.50 m～坡脚（设计河底高程）采用干砌方块石护坡，高程3.50，2.50 m处设消浪平台宽3.00m，堤基采用大开挖置换处理，堤身回填开山石渣。右岸堤防桩号2+220断面图如图6所示。

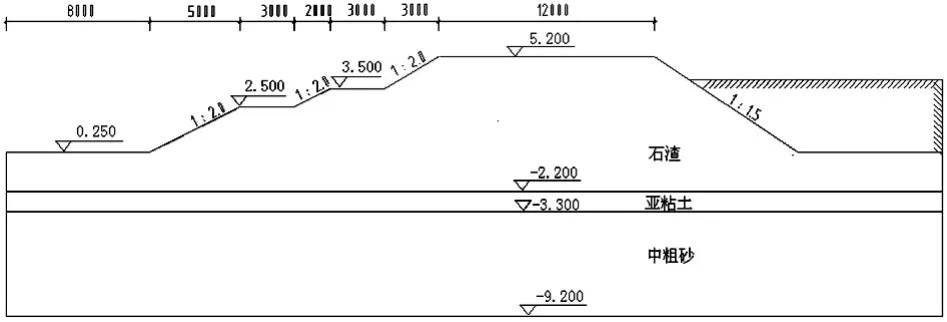
图6 某河流右岸堤防桩号2+220断面图

2.2 材料参数及计算工况

2.2.1 设计断面和材料参数

该河右岸堤防工程的设计断面如图6所示，各土层材料参数列入表1。

点强度参数折减法下和通用强度折减法下的土坡安全系数均可以较好地反映土坡的稳定性。根据《堤防工程设计规范》，对于3级建筑物，正常运用条件下，采用瑞典条分法计算的坝坡抗滑稳定安全系数≥1.20，非常运用条件的安全系数应≥1.10，由表2可知，各计算断面在各工况下的边坡稳定安全系数均大于规范要求值，满足稳定要求。工况2的安全系数小于工况1的安全系数，与前面位移分析时的预测相符。

从表中数据可以看出，点强度参数折减法下的土坡安全系数在情况1时，与瑞典条分法接近；在情况2时大于后者，约3%～6%。通用强度折减法下的土坡安全系数普遍小于强度参数折减法：在情况1时，也小于瑞典条分法下的安全系数，约5%～7%；情况2的土坡安全系数与瑞典条分法下的安全系数接近。由此可见，点强度参数折减法下的土坡安全系数在一定程度上虽然可以作为土坡稳定分析的代表值，但若从计算角度来看，它大于极限平衡法的上限值，从工程角度来看则偏于危险。而通用强度折减法下的土坡安全系数同样可以作为实际工程的代表值，从计算角度更为合理，从工程角度则更为安全。

表1 桩号2+220堤防断面坝基各土层物理参数统计表

2.2.2 计算工况和荷载情况

根据《堤防工程设计规范》（GB50286-98），该工程的地震设计烈度为6度，不进行抗震计算。由于该河设计洪水位比规划地面低，故仅对堤防临水侧边坡进行抗滑稳定计算，计算工况选取施工期、100年一遇设计洪水位3.84 m两种工况进行计算。

土坡的荷载情况为：两个设计工况均有重力荷载和堤顶荷载。运行期在浸润线下采用浮容重，不考虑临水侧水压力荷载。堤顶路段两侧是人群荷载，均布4 kPa，分布宽度每侧2.50 m。中间是汽车荷载，荷载值22.321 kPa，分布宽度7 m。不计地震荷载。

2.3 有限元计算结果分析

该模型是非均质成层多级土坡，采用单元形心处的主应力计算。因土坡为成层多级土坡，破坏型式为两次破坏过程，分别为第一级土坡破坏和整体土坡破坏。为了更好地直观计算结果，在此称第一级土坡破坏为情况1，土坡整体破坏为情况2。分别记录两个情况下的折减系数，列于表2。刚体极限平衡法的结果运用北京理正软件进行瑞典条分法下的边坡稳定安全系数，连同规范允许值一并列入表2。

表2 临水侧边坡稳定安全系数表

3 结语

基于临界极半径折减的的通用强度折减法对传统强度折减点安全系数的局限性进行改进，具有明确的物理意义和几何意义，且符合强度安全的度量方式。通过对岩土材料和混凝土材料的多种强度准则计算，文章定义的通用强度折减点安全系数能够正确地反映各种应力条件下的点安全度，具有良好的表征性。文章定义的强度折减点安全系数具有实用性，该边坡工程作为非均质成层多级土坡，是一个典型的人工复杂土坡。对于这样的实际工程，通用强度折减法仍然可以较好地反映土坡的稳定性，具有实际应用意义。

[1]钱向东，焦彩虹.基于多参数强度准则的安全系数定义问题[J].水利水电科技进展,2007,27(4)：34-37.

[2]陈惠发，A.F.萨里普.混凝土和土的本构方程[M].北京：中国建筑工业出版社，2004.

[3]钱向东，姜弘道.多轴强度安全系数的定义及应用[J].建筑科学与工程学报,2008,(1)：37-42.