冲击加载下煤岩破碎块度与能耗关系的试验研究*
刘晓辉 张 茹 刘建锋
(1.西华大学能源与环境学院,四川省成都市,610039;2.四川大学水利水电学院,四川省成都市,610065)
煤岩破碎是煤矿开采过程中最基本的过程,是爆炸冲击波与应力波和爆生气体共同作用的结果。不同开采速度、开采方式下,煤岩的破碎块度、吸收和释放能量的多少,对于评价破岩方法、研究破岩机理、决定开采方案以及选矿、采矿是至关重要的,它将直接影响矿产开采的生产效率。加之煤岩在破碎过程中,动、静态破碎机理有所不同,所产生的破坏形态、破裂特征也存在差异。考虑到在深部开采工程领域中,煤岩1~102s-1应变率段的动力特性的重要性,本文故采用大直径霍普金森压杆(SHPB)试验装置,以不同冲击加载速度对煤岩进行冲击压缩试验,意图弄清其瞬时变化特性和传播特性,借以探求煤岩破碎块度、破碎能耗两者之间的关系,为提高破岩效果提供试验理论依据。
1 试验简介
1.1 煤样制备
试验所用煤样系无烟煤,取自四川省芙蓉白皎煤矿,埋深300~450m,地层为宣威组第二段P2 X2。该区域煤岩矿物除方解石、高岭石、石英外,还含有非晶态矿物碳、氢、氧等。
将所取煤岩依据煤和岩石物理力学性质测定方法 (GB/T 23561.7-2009)在四川大学水利水电学院岩石制样室进行加工,制成∅50mm×L50mm标准圆柱体,保证煤岩试样两端面平行度在0.02mm范围以内。
1.2 试验设备
利用中国矿业大学 (北京)∅75mm霍普金森压杆 (SHPB)完成煤岩动态冲击压缩试验。试验设备中的撞击杆、输入杆、输出杆材质均为35CrMn合金钢,三者直径均为50mm,长度分别为400mm、2000mm、2000mm。
1.3 试验原理
霍普金森动态冲击试验是在一定的外加气压作用下,将压杆冲头以一定的冲击加载速度与输入杆发生对心碰撞,然后在输入杆端产生应力脉冲,该应力脉冲将向前传播,直至杆件与煤岩接触界面处发生反射和透射。经过几次透、反射过程后,在保证一维弹性波传播和煤岩与两端面的应力应变达到基本平衡的前提下,利用对称布置在输入杆和输出杆上的半导体应变片,结合TST3000动态测试仪,测量入射波、反射波和透射波的波形曲线和各时间历程所对应的电压值。
然后将该试验电压数据进行透、反射波的电压值标定,求出入射波εi、反射波εr和透射波εt。
再依据SHPB基本公式,如式 (1)所示,利用波的应变值,确定煤岩试样的动态应力σ、应变ε和应变率˙ε。
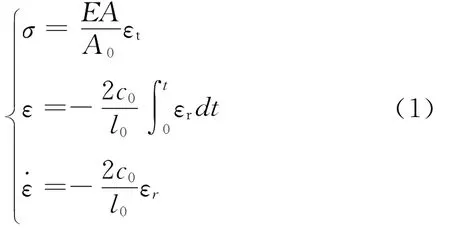
式中:σ——煤岩动态应力,MPa;
ε——煤岩动态应变;
——煤岩动态应变率,s-1;
εi、εr、εt——分别为入射波、反射波、透射波应变;
c0——压杆弹性波速,取5060m/s;
E——压杆材料的弹性模量,取200GPa;
A——压杆的横截面面积,mm2;
A0——煤岩试样原始横截面面积,mm2;
l0——煤岩试样原始长度,mm。
2 煤岩破碎块度特征
2.1 煤岩块度分形原理
煤岩在冲击加载下将发生最终的破碎现象,这种现象被认为是普遍存在的不规则、破碎且具有统计自相似性的现象,对于该现象利用分形几何法能够得到较好的分析。
目前,岩体的动力破坏块度分布函数使用最为广泛的有泊松分布、正态分布、伽马分布、Rosin-Rammler分布以及对数正态分布。而其中传统评价爆破破碎块度分布函数的是Rosin-Rammler函数:
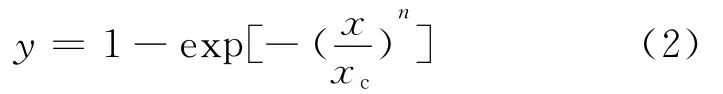
式中:x——破碎块体尺寸,mm;
xc——特征尺寸,mm;
n——曲线形状指数;
y——破碎块体尺寸小于等于x的累积质量百分比,%。
依据煤岩冲击破碎后粒度—质量关系确定其煤岩曲线形状指数,并根据分形原理,确定煤岩破碎块度的分形维数Dn与曲线形状指数n的关系为:

因此可以将冲击加载试验得到的破碎煤岩按不同尺度范围,采用筛分方法获得不同粒组范围的质量分布特性,然后再利用破碎块度分布的分形性质及岩石破碎学基本理论得出煤岩破碎块度分形维数和平均块度。
煤岩破碎平均块度的计算:
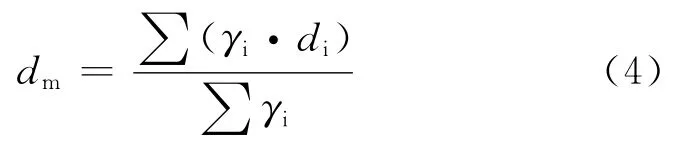
式中:dm——煤岩破碎平均块度,mm;
di——煤岩碎块的块度,mm;
γi——对应di的筛上碎块质量累计百分率,%。
2.2 煤岩破碎块度分析
由式 (2)~ (4)得到煤岩冲击加载下破坏块度分布测量数据,如表1所示。从表1可以看出,冲击加载下的煤岩,其应变率愈大,煤岩冲击破碎块度愈小,破碎愈严重,破碎数量愈多。
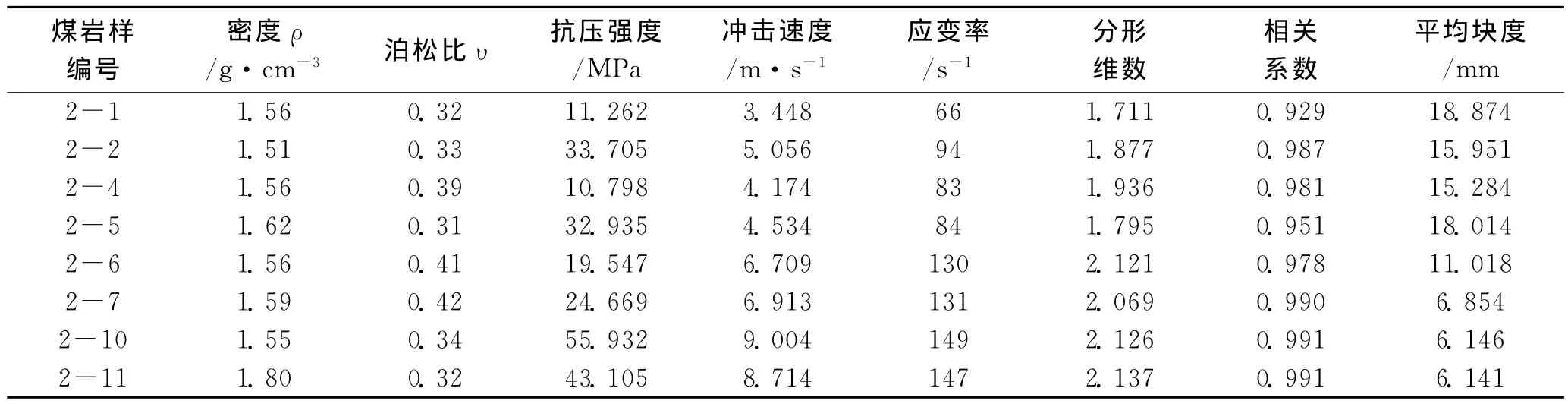
表1 煤岩冲击压缩试验破坏后碎块分布测量数据
为进一步分析煤岩冲击加载后平均块度与分形维数、应变率的关系,绘制图1和图2,发现破碎块度的分形维数能够定量地反映材料破碎的程度。分形维数愈大,应变率愈大,平均块度愈小,破碎块数愈多,体积愈小,破碎程度愈高;分形维数小的煤岩,所受应变率较小,块数少,平均块度大,破碎程度低。
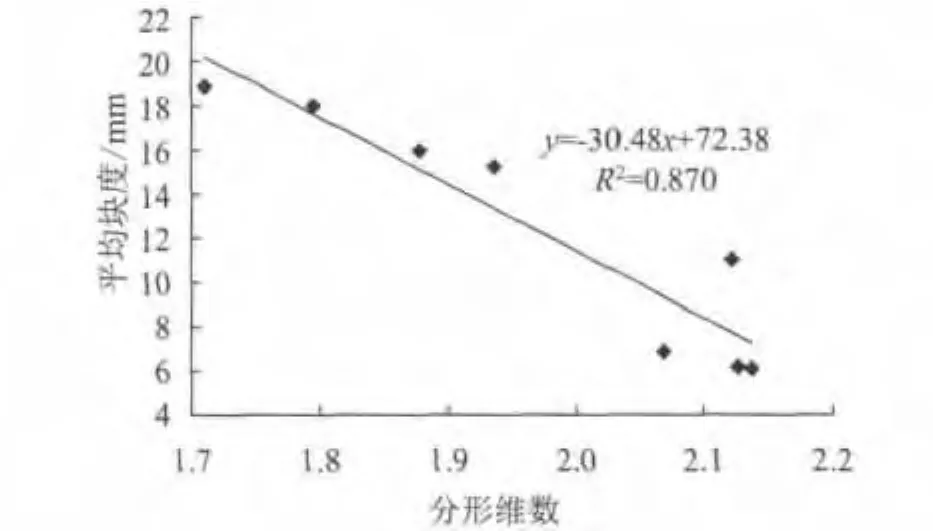
图1 平均块度与分形维数关系曲线
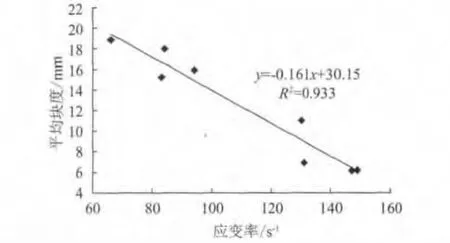
图2 平均块度与应变率关系曲线
3 煤岩破碎能耗特征
3.1 煤岩破碎能耗原理
煤岩的破碎过程是其内部缺陷不断萌生发育、扩展、聚集和贯通的最终结果,是一个从细观损伤发展到宏观破碎的过程,是能量耗散的过程。
霍普金森杆应力波所携带的能量计算:
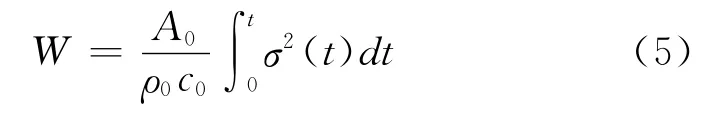
式中:W——3种应力波所携带的能量,J;
A0——输入与输出杆的横截面,mm2;
ρ0c0——杆的波阻抗,g/cm3·m/s;
σ(t)——杆的脉冲应力值,MPa。
在SHPB动态冲击过程中,煤岩能量耗散可以利用破碎能耗Wd、能量耗散率N和能耗密度ed来表征:
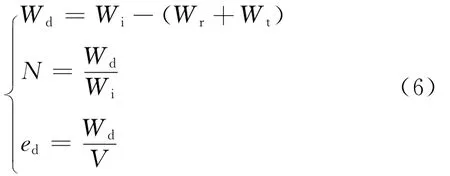
式中:Wd——破碎能耗,J;
N——能量耗散率,%;
ed——能耗密度,J/cm3;
Wi、Wr、Wt——分别为入射能、反射能和透射能,J;
V——煤岩体积,mm3。
3.2 煤岩破碎能耗分析
依据霍普金森杆动态冲击试验数据,由式 (5)和式 (6)得到煤岩破碎能耗分析表,见表2。
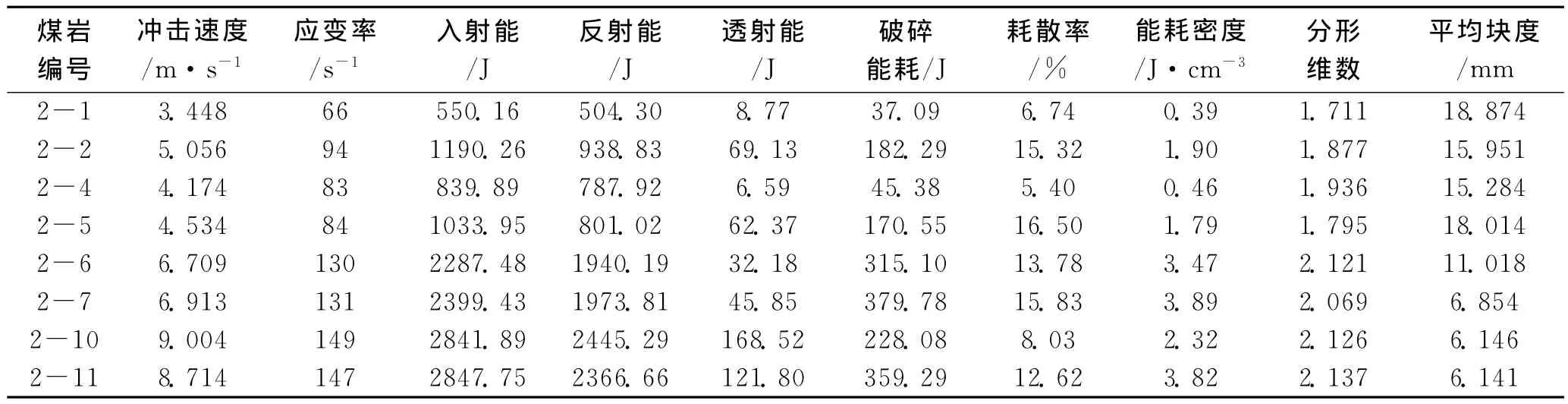
表2 煤岩破碎能耗分析
利用表2绘制冲击加载作用下煤岩的入射能、反射能、透射能以及破碎能耗分别与应变率和破碎平均块度的变化曲线,如图3所示。从图3(a)应变率—能量关系曲线中可以看出,随着应变率的增大,煤岩破碎过程中各能量都线性增大,入射能增长速度最大,反射、透射能增长速度相对较缓;从图3(b)平均块度—能量关系曲线可以看出,能量越小,煤岩的平均块度越大,其变化趋势基本为线性递减。因此可以得出,煤岩随冲击加载速度的增大,入射、反射、透射能量均增大,煤岩破碎程度越剧烈,破碎块度越小,破碎能耗越大。
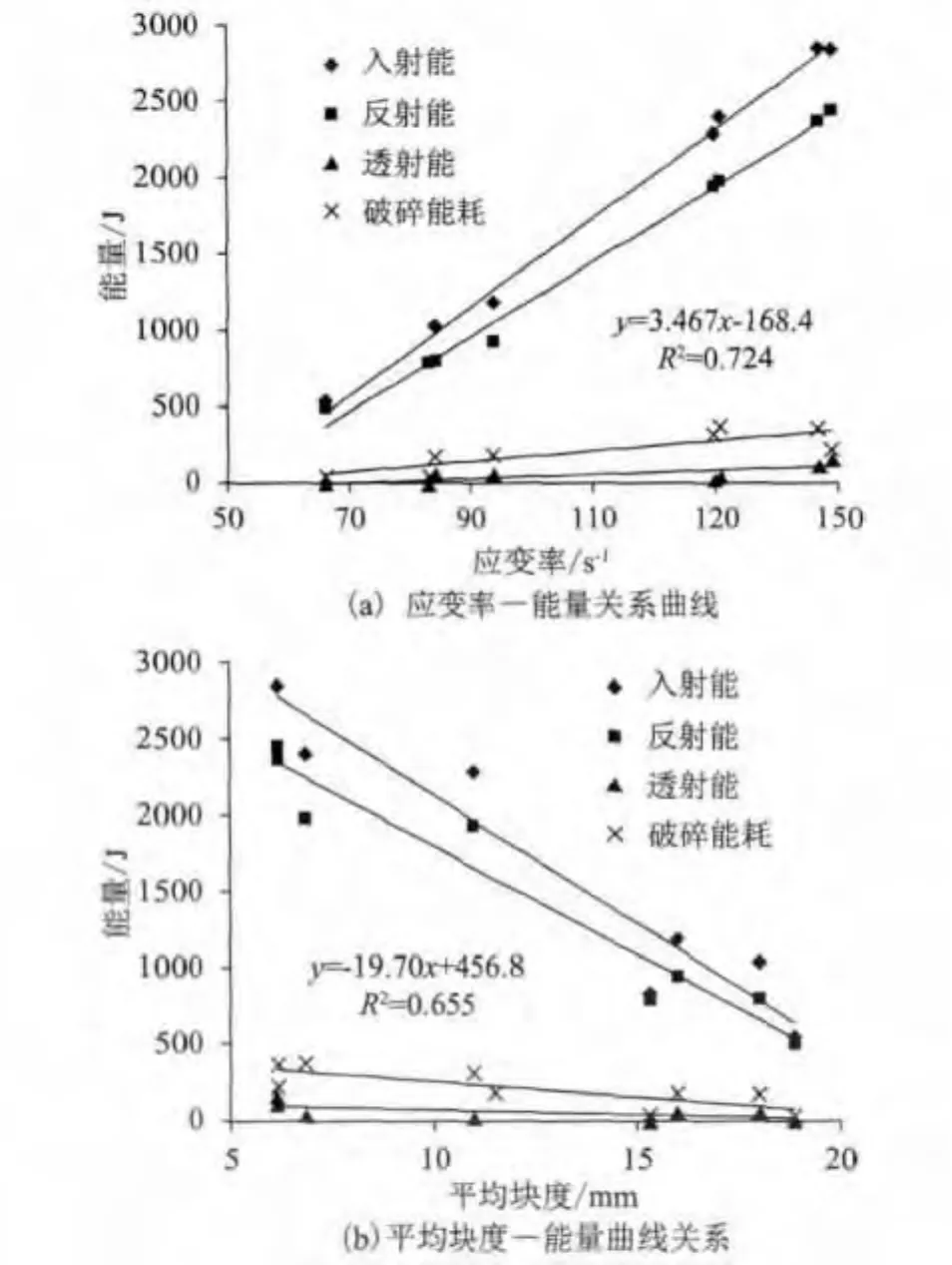
图3 煤岩能量变化曲线
能量耗散率能够反映出动态冲击下煤岩的能量耗散强弱。由表2可以看出,煤岩平均块度越大,其能量耗散率趋于越大,但是存在波动性,究其原因是由于煤岩离散性较大,能量在煤岩中的传播存在较大的差异性。
考虑单位体积煤岩能量耗散率与破碎平均块度的关系,绘制煤岩破碎平均块度与破碎能耗密度关系曲线,见图4。从图4中看出,煤岩破碎的平均块度随破碎能耗的增加而减少,破碎块度愈大,能耗密度愈小,单位体积煤岩破碎的表面积越小,即破碎能耗与破碎块体的表面积成正比。
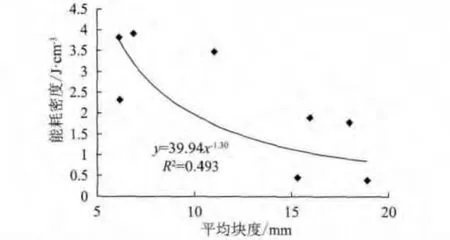
图4 煤岩破碎能耗密度与破碎平均块度关系曲线
4 结论
根据煤岩在不同冲击加载速度下SHPB压缩试验以及对破碎煤岩的能耗、块度分析,得出以下结论:
(1)煤岩破碎程度及脆性性质可以用分形维数来反映。分形维数愈大,平均块度愈小,破碎程度高,材料愈脆,破碎时呈爆裂破碎;分形维数小,平均块度大,破碎程度低,材料脆性降低,破碎时存在局部剪切滑动现象。
(2)煤岩随冲击加载速度的增大,对应入射能、反射能、透射能相应增大,煤岩越破碎,破碎块度越小,破碎能耗越大。
(3)煤岩破碎块度随破碎能耗的增加而减少,破碎块度愈大,能耗密度愈小,单位体积煤岩破碎的表面积越小,破碎能耗与破碎块体的表面积成正比关系。
[1]尚海涛,吴健.论综放开采技术在我国发展的必然性[J].中国煤炭,1997 (4)
[2]钱鸣高.煤炭的科学开采及有关问题的讨论[J].中国煤炭,2008(8)
[3]孙强,段法兵,谢和平.煤体爆破破碎分维评价方法的研究[J].岩石力学与工程学报,2000(4)
[4]李胜林,刘殿书,李祥龙等.∅75mm分离式普金森压杆试件长度效应的试验研究[J].中国矿业大学学报,2010 (1)
[5]李夕兵,古德生.岩石冲击动力学[M].长沙:中南工业大学出版社,1994
[6]胡时胜.霍普金森压杆技术[J].兵器材料科学与工程,1991 (11)
[7]谢和平.分形理论在采矿科学中的应用与展望[A].跨世纪的矿业科学与高新技术[C].北京:煤炭工业出版社,1996
[8]戚承志,王明洋,钱七虎等.爆炸作用下岩石破裂块度分布特点及其物理机理[J].岩土力学,2009(S1)
[9]何满潮,杨国兴,苗金丽等.岩爆实验碎屑分类及其研究方法[J].岩石力学与工程学报,2009(8)
[10]杜晶,李夕兵,宫凤强等.岩石冲击实验碎屑分类及其分形特征[J].矿业研究与开发,2010(5)
[11]徐小荷,余静.岩石破碎学[M].北京:煤炭工业出版社,1984
[12]李启月,顾春宏,李夕兵等.冲击加载下矽卡岩破碎能耗与块度关系的试验研究[J].矿冶工程,2009(4)

