带抽头电感的准Z 源逆变器建模与特性分析

赵健伍 黄文新 周玉斐 焦荣惠

（1.南京航空航天大学江苏省新能源发电与电能变换重点实验室 南京 210016 2.中国空间技术研究院通信卫星事业部 北京 100094）

1 引言

随着电动汽车驱动、起动发电等技术的开发应用，以及可再生能源发电的大力发展，对电力电子逆变技术的性能、可靠性等提出了越来越高的要求。传统的逆变电路分为两类:电压源逆变器和电流源逆变器；电压源逆变器输入直流电压输出交流电压，在电力传动方面应用非常广阔。一般来说，中小功率的交流电力传动系统都是基于电压源逆变器的，然而这种电压源逆变器存在着一些局限或不足[1]。

基于此，2002 年学者彭方正提出了一种Z 源逆变器（Z-Source-Inverter，ZSI）拓扑[2,3]，该拓扑在传统的电压源逆变器中引入了一个Z 源网络，将逆变器的主电路与直流电源耦合，使逆变器可以克服传统电压源逆变器的不足；同时由于Z 源逆变器在拓扑中引入了储能电感和电容，使得其可以利用传统电压源逆变器所不允许的直通零矢量状态，实现逆变器输出电压高于输入电压，而这也是传统电压源逆变器所不可能出现的情况。

虽然Z 源逆变器能够有效地调节逆变器直流母线电压的大小，并能克服传统电压源逆变器的局限，但是由于Z 源逆变器存在一些不足[4,5]:①逆变器母线电压低于电容电压，不能充分利用电容的电压等级，如果是高压应用场合，需要高压电容，体积较大；②只能通过控制逆变桥臂的直通零矢量来调节母线电压，升压能力有限，过大的直通占空比反而会减小调制度和输出电压幅值。这些不足大为限制了Z 源逆变器的适用范围。

随后的研究中，学者安德森在传统Z 源逆变器的基础上提出了4 种准Z 源逆变器（quasi-ZSI，qZSI）[6]拓扑，它们与Z 逆变器的基本原理大致相同，理论上，适用于Z 逆变器的控制方法都可以用于准Z 逆变器。文献[6]总结了准Z 逆变器的特点，与Z 逆变器相比其无源器件的电压电流定额更低，开关器件的电压应力更小，但并没有从根本上克服Z 逆变器的局限性。

本文对一种带抽头电感的准Z 逆变器（Tappedinductor Z-Source-Inverter，TL-qZSI）进行研究[7]，通过对比传统ZSI 及qZSI，本文所论述的TL-qZSI具有更高的升压能力，更小的电容电压应力，并且不存在升压网络电感电容高度对称的问题；与此同时，通过合理设计抽头电感Lt的匝比[8,9]和控制逆变桥臂直通零矢量可实现大压差范围转移传递电能。本文通过分析TL-qZSI 的各种工作模态，使用状态空间平均法[10]，建立了其直流侧小信号模型，并根据控制量与输出量之间的传递函数，对升压网络参数及直通占空比变化对系统的影响进行了分析；此外为了提高系统的动态性能及补偿非最小相位特性，设计了闭环调节器。最后通过仿真和实验验证了拓扑的上述特性。

2 抽头电感准Z 源逆变器

2.1 拓扑简介

图1 为带抽头电感的准Z 源逆变器拓扑，该拓扑用抽头电感Lt、二极管VD2、VD3代替了文献[6]qZSI 拓扑中的电感L2。由于引入了抽头电感Lt，使该拓扑在获得与传统Z 源逆变器、准Z 源逆变器相同升压比的情况下，所需的直通占空比更小，增大了调制度范围[8]，在异步电机调速等应用场合，能减小电机铁损耗[12]；同时由于抽头电感Lt的存在，可大为减小电容C1、C2的容量，以至于可用无极性电容替代电解电容，能有效的延长变换器的寿命及提高系统可靠性。

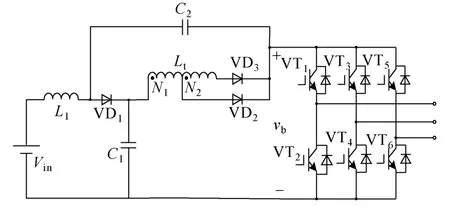
图1 带抽头电感的准Z 源逆变器拓扑Fig.1 Main circuit of TL-quasi-Z-source inverter

2.2 拓扑模态分析

图2 为TL-qZSI 在各模态下的等效电路图。直通零矢量状态时，逆变桥直通，等效为短路；传统零矢量状态时，逆变桥等效为开路；有效矢量状态时，逆变桥等效为电流源iload。同时假设电容C1、C2足够大，使电容电压在各状态变化中保持恒定。

（1）直通零矢量状态:如图2a 所示，电容C1电压大于输入电压源电压Vin，二极管VD1截止；电容C1通过抽头电感一次绕组N1放电，一次绕组N1中电流从最小值开始上升，此时一次绕组N1两端电压左“+”右“-”，感应到二次绕组N2的电压左“+”右“-”，且大于一次绕组N1两端电压，二极管VD3截止，即vN1=vC1；电容C2和输入电压源电压Vin串联给电感L 充电，即vL=Vin+vC2。

（2）传统零矢量状态:如图2b 所示，一次绕组N1电流停止增加，从最大值开始下降，感应到二次绕组电压左“-”右“+”，一次绕组N1与二次绕组N2串联，给电容C2充电，即vLt=vC2；二极管VD1导通，输入电源电压Vin和电感L 串联给电容C1充电，电感L 电流从最大值下降，即vL=vC1-Vin。

（3）有效矢量状态:如图2c 所示，一次绕组N1与二次绕组N2串联继续释放能量，vLt=vC2；输入电源电压Vin与电感L 串联，继续给电容C1充电，vL=vC1-Vin。

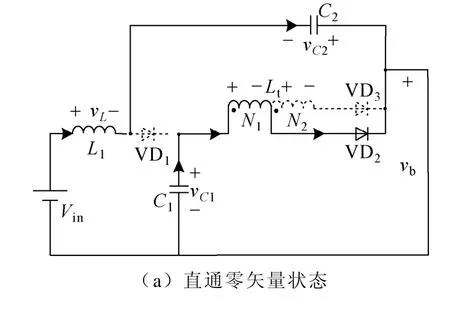
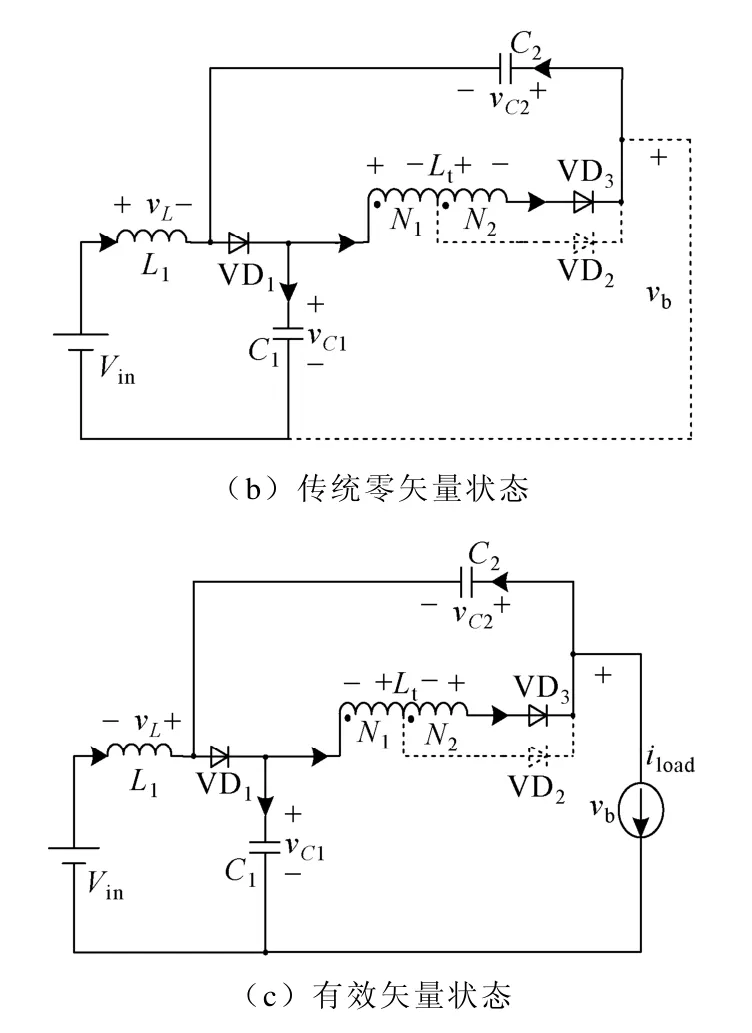
图2 带抽头电感的准Z 源逆变器拓扑模态图Fig.2 Equivalent circuit under three switching states

根据电感的伏秒特性，即整个周期内电感的平均电压等于0，整理可得

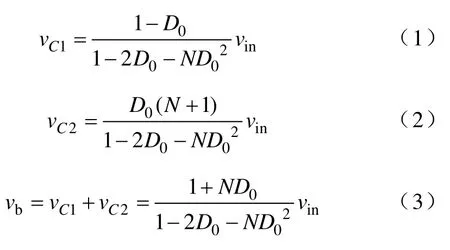
式中，D0为直通占空比；N 为抽头电感匝比。

2.3 拓扑特性比较

根据式（1）～式（3）、文献[2,6]可知，在简单升压控制下，带抽头电感的准Z 源逆变器、传统Z源逆变器、传统准Z 源逆变器的相关特性见下表。

表 三种拓扑特性Tab. Properties of three topological

图3 为三种拓扑特性比较，可以看出，TL-qZSI在相同直通占空比下升压能力较传统ZSI、qZSI 高；在相同电压增益下最大调制度较传统ZSI、qZSI 高，大的调制度能减小逆变器输出电压的谐波含量，获得较好的输出波形；在相同升压比下电容C1电压应力较传统ZSI、qZSI 低；在相同直通占空比下，母线电压vb与电容电压vC1的比值最大，即在相同电容电压vC1下，TL-qZSI 母线电压vb最高，可认为TL-qZSI 较传统ZSI、qZSI 更能够利用电容电压等级，即便是高压应用场合，需要的电容耐压值更小，体积更小；与此同时，随着抽头电感匝比N 的增加，TL-qZSI 的上述特性更明显。

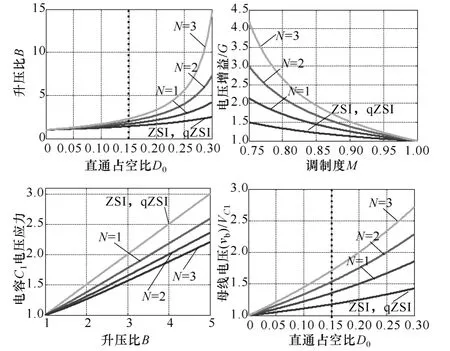
图3 三种拓扑特性比较Fig.3 Feature comparison of three topology

3 带抽头电感的小信号模型

为了进一步分析TL-qZSI 拓扑的内在特性，需建立TL-qZSI 较完整的小信号模型。升压网络中电感、电容作为重要储能元件，参与各模态的能量传递，其等效内阻对于研究拓扑特性及构建系统控制器具有重要意义，故在建模中，考虑电容等效串联电阻RC1、RC2，电感寄生电阻rL、rLt、rLp[13]；同时，根据文献[9]分析，忽略抽头电感漏感的影响。

3.1 模型建立

TL-qZSI 拓扑在直通零矢量时，抽头电感一次绕组储能；非直通零矢量状态时，抽头电感一次绕组和二次绕组串联给负载供电，因此抽头电感一次绕组电流iLp能够反应整个周期中抽头电感的状态变化。故选取抽头电感一次电流iLp、输入电感电流iL1及升压网络中电容电压vC1、vC2作为状态变量，构建状态方程。

3.1.1 直通零矢量状态

3.1.2 非直通零矢量状态

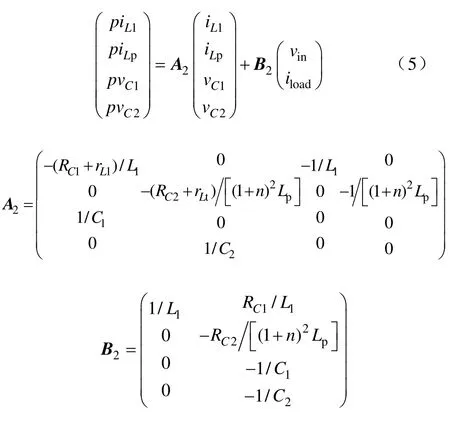
3.1.3 状态空间方程

综合考虑直通零矢量状态与非直通零矢量状态，在一个周期内取状态平均

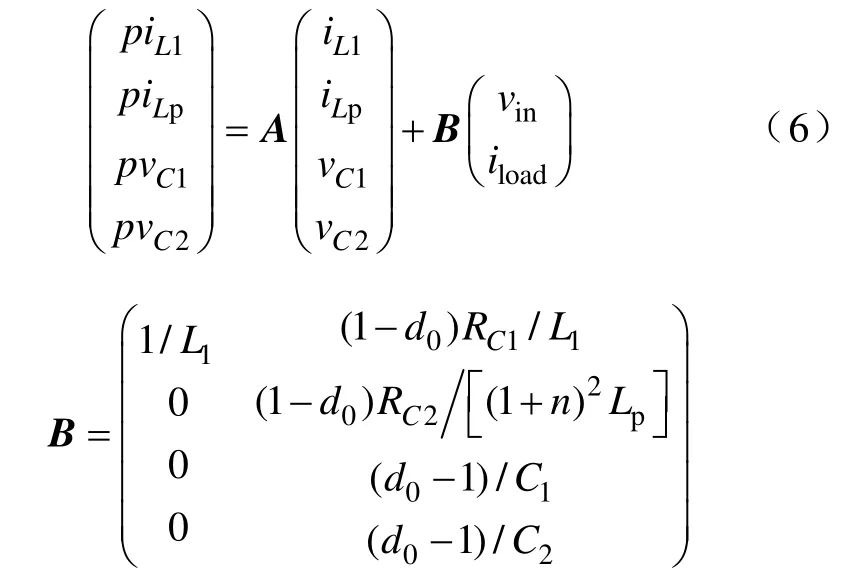
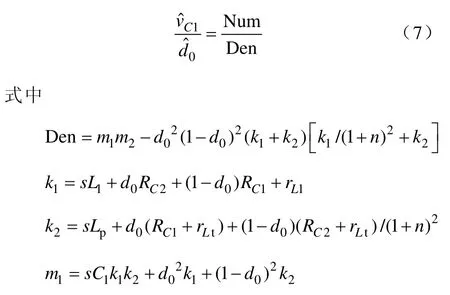
3.2 TL-qZSI 拓扑参数变化分析

为了定性认识TL-qZSI 拓扑各参数及直通占空比变化时对系统性能指标如超调量、动态响应、负向幅值等的影响，分别对TL-qZSI 拓扑电感取值、电容取值、内阻取值及直通占空比取值变化，并观察系统零极点分布情况。此处选定一组参数:L1=1.0mH，Lp=800µH，N=3，C1=10µF，C2=100µF，rLp=0.06Ω，rLt=0.5Ω，rL1=0.1Ω，RC1=0.01Ω，RC2=0.02Ω，d0=0.09，在此基础上分析系统零极点变化，相应的结果如图4 所示。

3.2.1 电感取值变化

输入电感L1增大，右半平面零点沿实轴向原点移动，系统非最小相位特性加剧，负向超调幅值增大；极点沿着虚轴向原点移动，系统阻尼增大，动态响应变慢。

抽头电感由于互感的存在，不同于普通电感对系统的影响。图4b、图4c 所示为抽头电感一次电感值及匝比变化时的零极点分布图，可以看出，当抽头电感一次电感Lp及匝比N 增大时，系统右半平面零点沿着实轴方向远离原点，系统非最小相位特性减弱，负向超调幅值减小；极点沿着虚轴向原点移动，系统阻尼增大，动态响应变慢。

图4 TL-qZSI 拓扑参数变化系统零极点分布图Fig.4 Pole-zero locus if the control-to-capacitor-voltage function with different parameters of TL-quasi-Z-source

3.2.2 电容取值变化

如图4d、图4e 所示，电容C1、C2值增大，右半平面零点位置保持不变，系统负向超调幅值不变；极点沿着虚轴向原点靠近，系统阻尼增大，动态响应变慢。

3.2.3 内阻取值变化

如图4f 所示，内阻RC1值增大，右半平面零点沿实轴向原点移动，系统非最小相位特性加剧，负向超调幅值增大，但由于极点远离虚轴，系统输出衰减振荡，会使系统最终输出负向超调幅值减小。

如图4g 所示，内阻rLp值增大，右半平面零点沿实轴远离原点，系统非最小相位特性减弱，负向超调幅值减小；极点远离虚轴，系统输出衰减振荡。

通过上述分析发现，较大的电感和电容值，能够获得较好的稳态特性，器件电压电流纹波较小；但系统会表现出较差的动态响应，因此在设计实际系统时，应根据应用场合合理选取二者的参数。

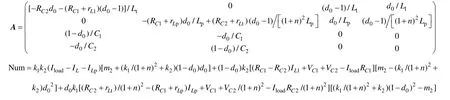
3.2.4 直通占空比取值变化

TL-qZSI 由于能够实现大压差范围转移传递电能，适用于燃料电池电动汽车驱动等场合，当电池端电压跌落时，通过控制直通零矢量可以有效补偿电压跌落，此时TL-qZSI 直通占空比的变化对于逆变器输出性能有很大影响。

如图4h 所示，当直通占空比d0值增大时，右半平面零点沿着实轴向原点移动，系统负向超调幅值增大；极点沿着虚轴向原点移动，系统阻尼增大，动态响应变慢。

4 闭环控制器设计

4.1 系统分析

根据系统开环传递函数可知TL-qZSI 拓扑为六次高阶系统，其动态性能指标的确定比较复杂；且由于该非最小相位系统存在两对对消的零极点，以及系统表现的欠阻尼特性，在设计闭环调节器时应格外注意。

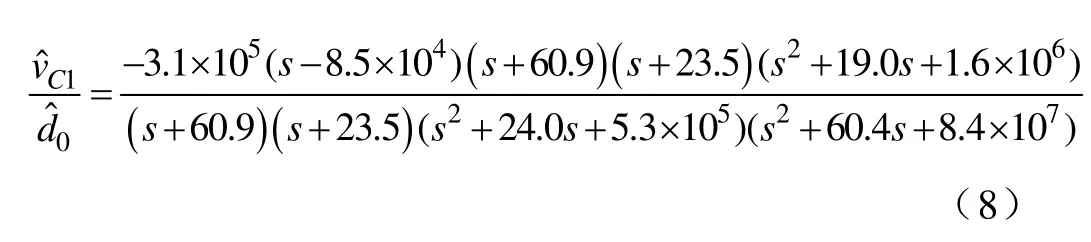
4.2 闭环设计

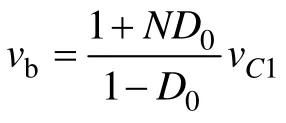
图6a 上半部分曲线为无母线电压闭环调节器时系统的幅频特性曲线，可以看出幅值裕度Ag=-74.1dB，相位裕度γ=-75.3°，为不稳定系统。同时考虑在设计调节器时，系统穿越频率必须低于右半平面零点的频率，即在TL-qZSI 中右半平面零点的频率为85kHz，因此闭环系统的带宽可以适当放大以保证系统的动态响应；此外由于该拓扑具有非最小相位特性，系统输出响应会出现负向的超调。

基于上述分析，对于TL-qZSI 拓扑所示的高阶系统，采用实际工业应用中常用的PID 调节器构造母线电压闭环，其欠阻尼特性可以被近似为惯性对象，虽然忽略的振荡特性有可能引起控制品质的恶化，但是能很大程度上简化闭环控制器的设计。此处采用PID 调节器设计母线电压闭环，用以得到稳定的输出，以及改善非最小相位特性，同时加快系统动态响应。

如图5 所示为简化后的TL-qZSI 母线电压闭环调节器框图，其中 Gvd(s) 为电容C1电压扰动与直通占空比扰动 dˆ0之间的传递函数，Gpi(s) 为PID调节器，根据系统稳定性与动态响应的要求，母线电压闭环调节器为[11]

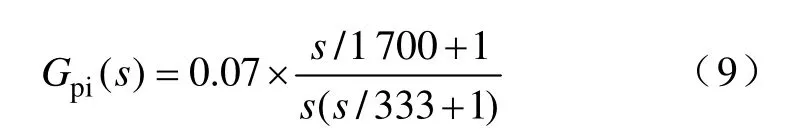
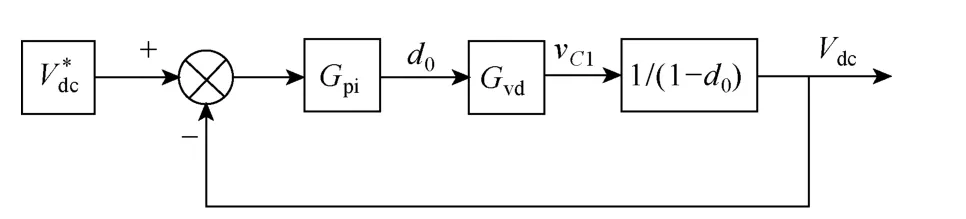
图5 简化后母线电压闭环控制框图Fig.5 Simplified voltage loop controller configuration

图6a 下半部分曲线为加入母线电压闭环调节器后系统的伯德图，此时幅值裕度Ag=20.7dB，相位裕度γ=82.2°，该系统稳定性很好，且穿越频率为640Hz。图6b 为加入母线电压调节器后系统的阶跃响应图，可以看出本文所采用的闭环调节器参数能使系统较快达到稳定状态，且无超调。

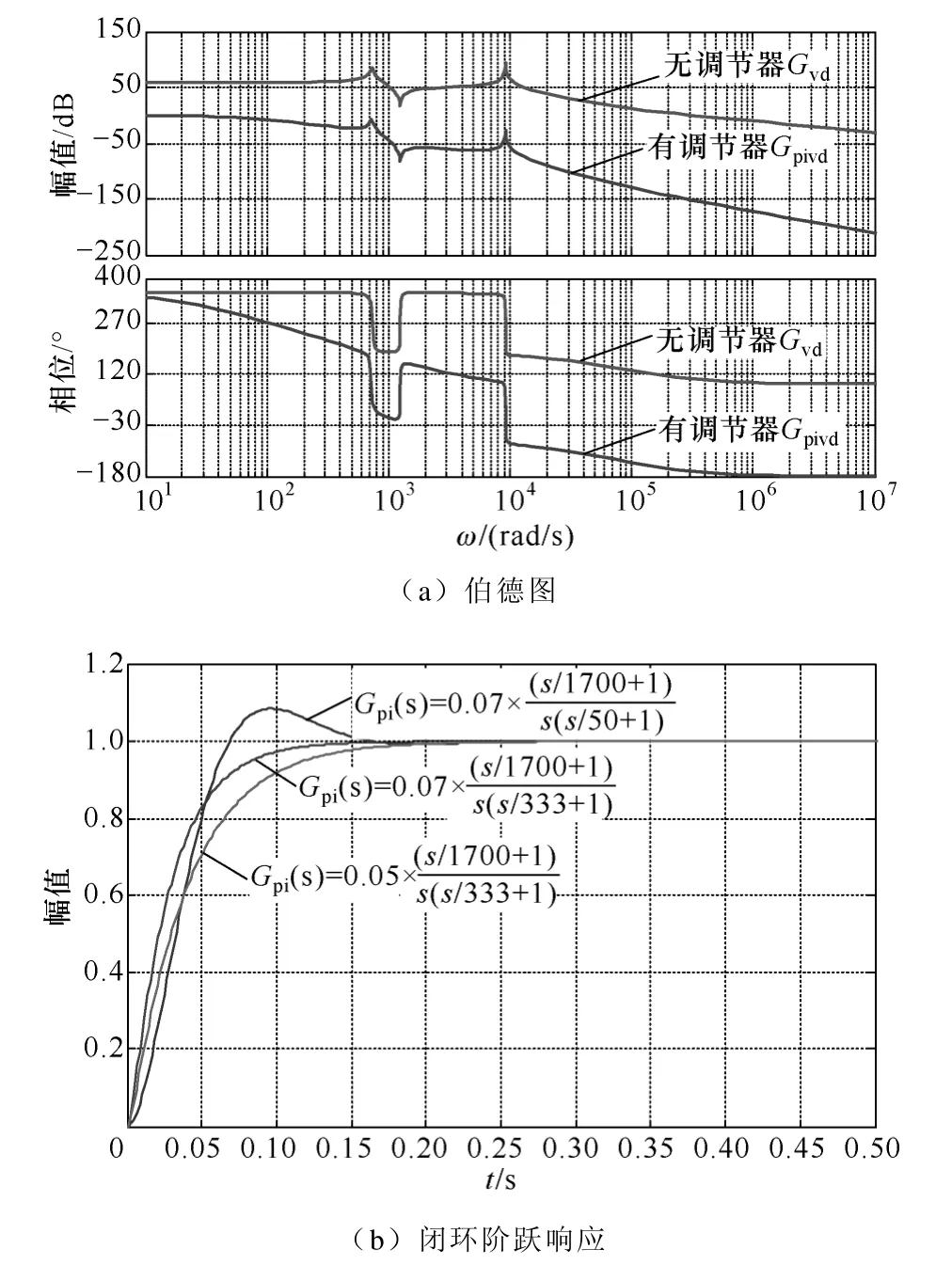
图6 系统伯德图和阶跃响应图Fig.6 Bode plot and step response with PID controller

5 TL-qZSI 的特性仿真与实验验证

为了验证前述理论分析，使用3.2 节中系统参数，分别在Matlab/Simulink 以及TL-qZSI 实验平台上对拓扑特性进行研究。

5.1 仿真研究

5.1.1 拓扑特性

搭建TL-qZSI 仿真模型，使用简单升压控制方式，令输入电压Vin=220V，直通占空比d0=0.09。仿真结果如图 7a 所示，TL-qZSI 直流母线电压vb=360V，升压比B≈1.64；在相同直通占空比下，ZSI、qZSI 的母线电压为vb=270V，升压比B≈1.22，可以看出TL-qZSI 较ZSI、qZSI 具有更高的升压能力。图7b 为电容电压应力仿真结果，电容C1电压应力VC1=252V，电容C2电压应力VC2=99V，在相同升压比下，ZSI、qZSI 的电容 C1电压应力为VC1=289V；电容 C2应力分别为 VC2(ZSI)=289V，VC2(qZSI)=69V，可以看出TL-qZSI 较ZSI、qZSI 的电容C1电压应力更低，较ZSI 电容C2电压应力更低。

同时，根据前述TL-qZSI 拓扑参数变化对系统的影响，碍于文章的篇幅，此处仅给出抽头电感参数变化对系统的影响。选取两组参数:Lp1=220µH，N1=2.5；Lp2=800µF，N2=3。图7c、图7d 所示为0.1s直通占空比变化时系统的输出响应，可以看出当抽头电感一次电感Lp及匝比N 增大时，系统非最小相位特性减弱，负向超调幅值减小，动态响应变慢，与前述理论吻合。

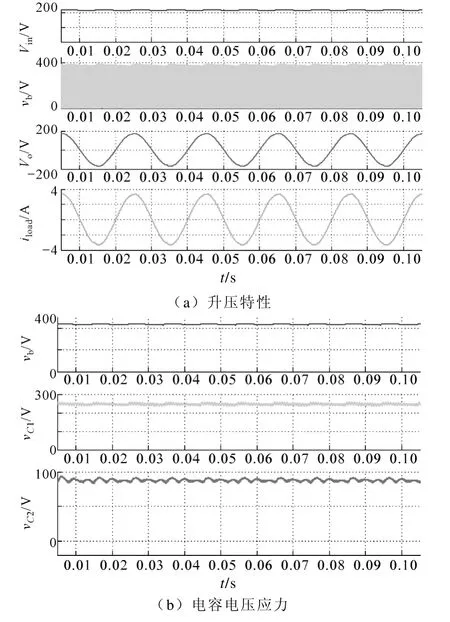
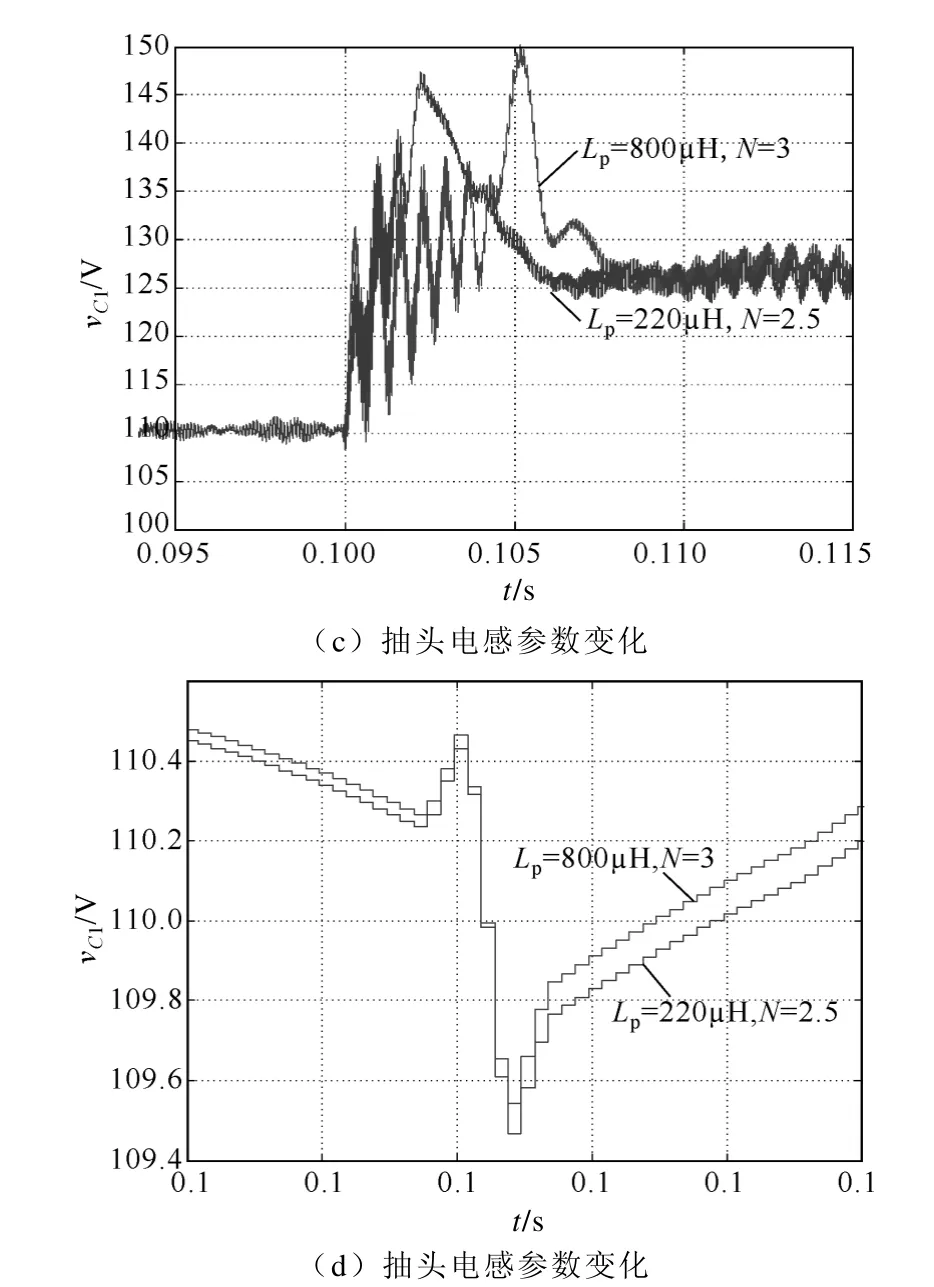
图7 特性仿真结果Fig.7 Characteristic simulation results

5.1.2 母线电压闭环特性

在TL-qZSI 仿真模型上构建前述母线电压闭环调节器，分别进行输入电压变化、负载变化实验，观察直流母线电压动态响应。图8a、图8b 为输入电压在Vin=140V 与Vin=195V 之间突升、突降时的直流母线电压动态响应，可以看出，系统通过母线电压闭环调节器调节输出量d0，能使母线电压保持稳定；图8c、图8d 为负载电流在I=2.9～1.5A 之间突增、突卸时的系统仿真波形，可以看出，直流母线电压依然能保持稳定。

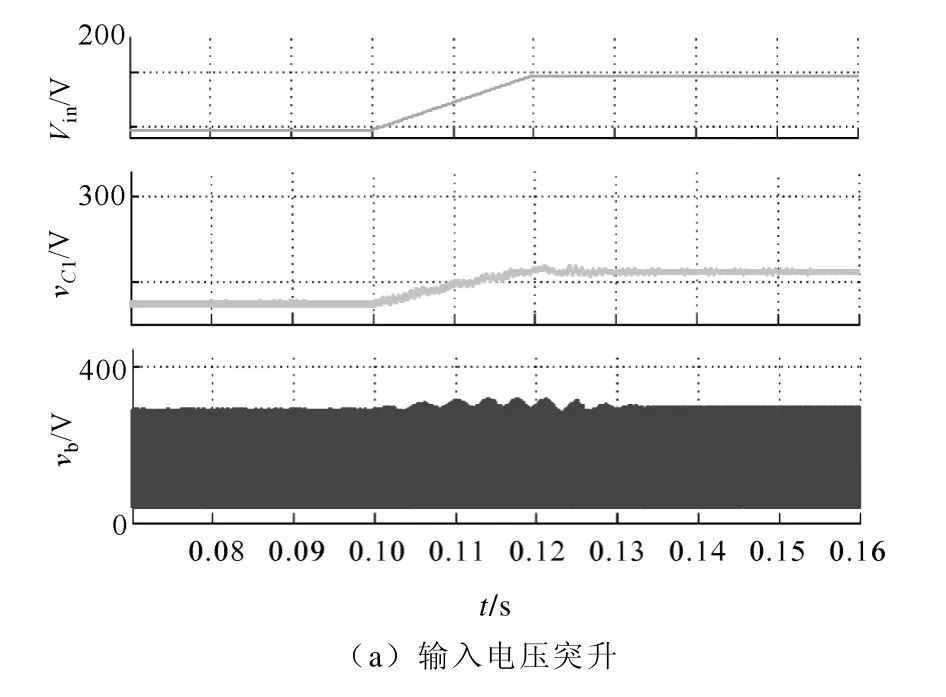
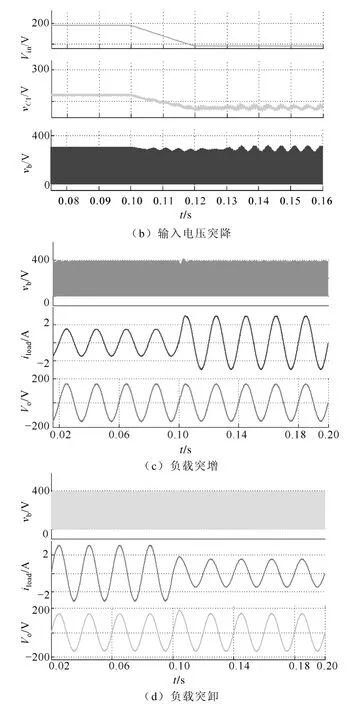
图8 动态特性仿真结果Fig.8 Dynamic behavior simulation results

5.2 实验验证

5.2.1 拓扑特性

在TL-qZSI 实验平台上进一步的对理论分析进行验证。图9a、图9b 分别为拓扑升压特性与电容电压应力实验结果，可以看出，当输入电压Vin=220V时，母线电压vb=360V，升压比B≈1.64，且电容C1电压应力VC1=250V，电容C2电压应力VC2=100V，与理论计算吻合。

同时，图9c、图9d 分别为抽头电感Lp1=220µH，N1=2.5；Lp2=800µF，N2=3 时的输出响应，可以看出系统负向超调幅值减小，动态响应变慢。由于实验采样自制的抽头电感，其寄生参数会一定程度上引起输出响应的振荡，后续的实验中会考虑此问题。

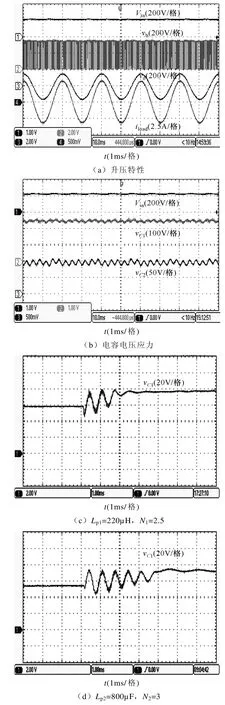
图9 TL-qZSI 特性实验结果Fig.9 Characteristic experimental results

另一方面，根据前述分析可知，TL-qZSI 在相同升压比下，最大调制度较ZSI、qZSI 高，即表现为系统输出电压谐波含量更小。图10 为负载电流I=2.9A 时，TL-qZSI 输出功率与输出电压THD 实验数据，可以看出TL-qZSI 有较好的电压输出特性。

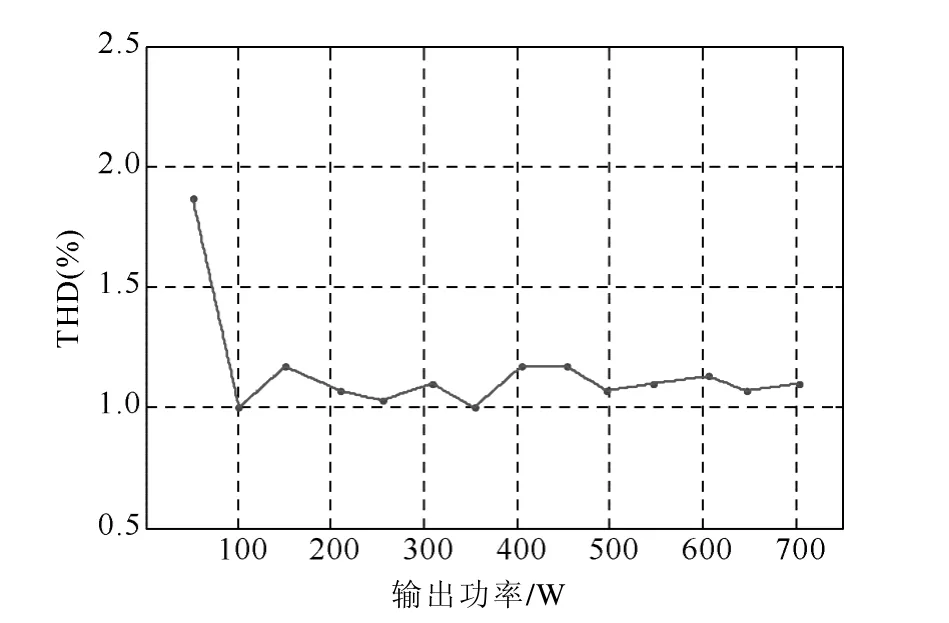
图10 THD 与输出功率特性Fig.10 THD and output characteristic

5.2.2 母线电压闭环特性

图11a、图11b，图11c、图11d 分别为TL-qZSI在输入电压Vin=140～195V，负载电流I=2.9～1.5A之间突变，系统的动态响应，可以看出，TL-qZSI直流母线电压保持稳定，系统有较好的动态响应。

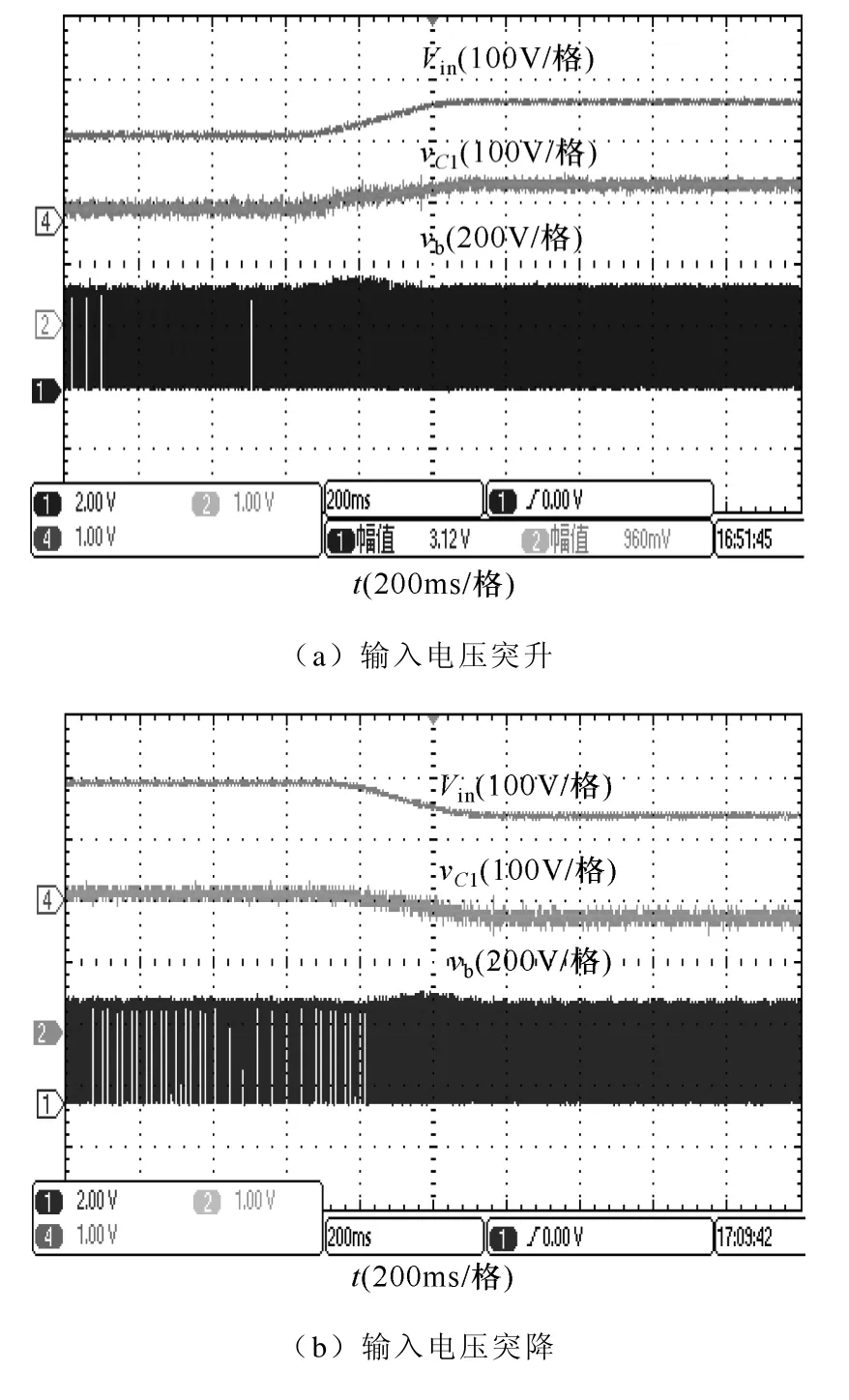
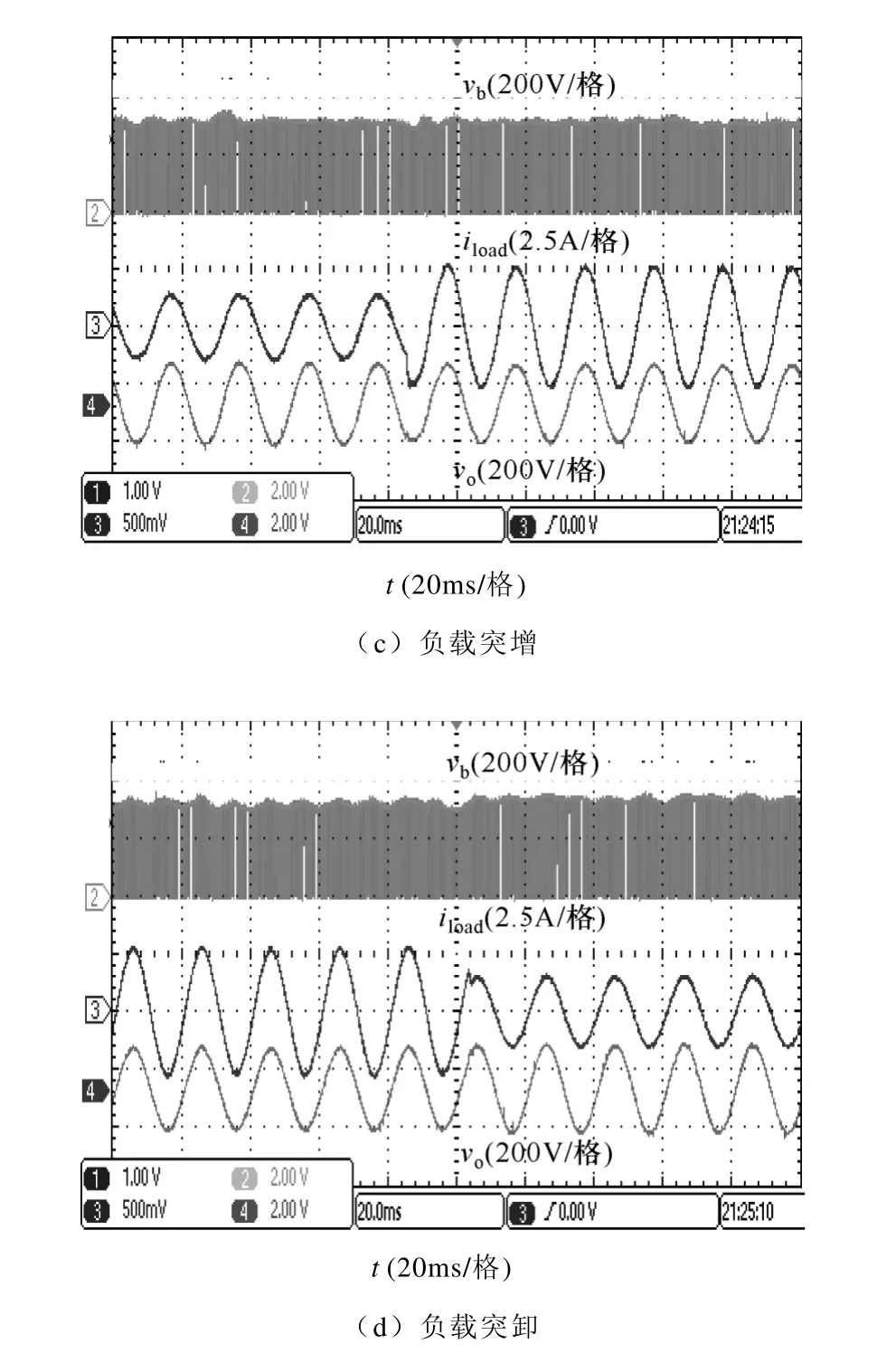
图11 动态特性实验结果Fig.11 Dynamic behavior experimental results

6 结论

本文对一种带抽头电感的准Z 源逆变器进行了研究，通过研究发现，该拓扑具有以下特点:

（1）控制方法上继承了Z 源逆变器的控制思想，运用直通零矢量使逆变器直流母线电压得到提升，提高了逆变器的可靠性，且避免了由于加入死区时间造成的输出波形畸变。

（2）通过合理设计抽头电感（Lt）的匝比和控制直通零矢量的长度可实现大压差转移传递电能，并可灵活地配置无源器件满足不同应用要求，比传统Z 源逆变器、准Z 源逆变器增加了一个可控制变量。

（3）相比于Z 源逆变器、准Z 源逆变器，该拓扑的直流母线电压能充分利用电容的电压等级。

（4）通过合理设计母线电压闭环调节器，TL-qZSI 系统具有较好的动态响应。

基于以上特点，带抽头电感的准Z 源逆变器拓扑具有更广阔的应用前景。

[1]杨奇,黄文新,胡育文,等.新型单级可升压逆变器[J].电工技术学报,2011,26(4):122-127.Yang Qi,Huang Wenxin,Hu Yuwen,et al.A novel single stage Boost inverter[J].Transactions of China Electrotechnical Society,2011,26(4):122-127.

[2]Fang Z P.Z-source inverter[J].IEEE Transactions on Industry Applications,2003,39(2):504-510.

[3]Fang Z P,Joseph A,Jin W,et al.Z-source inverter for motor drives[J].IEEE Transactions on Power Electronics,2005,20(4):857-863.

[4]Yu T,Shaojun X,Chaohua Z,et al.Improved z-source inverter with reduced z-source capacitor voltage stress and soft-start capability[J].IEEE Transactions on Power Electronics,2009,24(2):409-415.

[5]Zhou Yufei,Huang Wenxin.Single-stage boost inverter with coupled inductor[J].IEEE Transactions on Power Electronics,2012,27(4):1885-1893.

[6]Anderson J,Peng F Z.Four quasi-Z-Source inverters[C].Proceedings of the IEEE Power Electronics Specialists Conference(PESC),2008:2743-2749.

[7]周玉斐,黄文新,胡育文.带抽头电感的单级升压逆变器[P].2011.

[8]Miao Z,Ding L,Poh C L,et al.Tapped-inductor Z-source inverters with enhanced voltage boost inversion abilities[C].2010 IEEE International Conference on Sustainable Energy Technologies(ICSET),2010:1-6.

[9]Zhou Y,Zhao J,Huang W,et al.Tapped inductor quasi-Z-source inverter[C].Proceedings of the 27th IEEEApplied Power Electronics Conference and Exposition(APEC),2012:1625-1630.

[10]Yushan L,Baoming G,Ferreira F J T E,et al.Modeling and SVPWM control of quasi-Z-source inverter[C].Proceedings of the IEEE 11th International Conference on Electrical Power Quality and Utilisation(EPQU),2011:1-7.

[11]周玉栋,许海平,曾莉莉,等.电动汽车双向阻抗源逆变器控制系统设计[J].中国电机工程学报,2009,39(36):101-107.Zhou Yudong,Xu Haiping,Zeng Lili,et al.Control system of bi-directional Z-source inverter for electrical vehicle[J].Proceedings of the CSEE,2009,39(36):101-107.

[12]Poh C L,Vilathgamuwa D M,Lai Y S,et al.Pulsewidth modulation of Z-source inverters[J].IEEE Transactions on Power Electronics,2005,20(6):1346-1355.

[13]Poh C L,Vilathgamuwa D M,Gajanayake C J,et al.Transient modeling and analysis of pulse-width modulated Z-source inverter[J].IEEE Transactions on Power Electronics,2007,22(2):498-507.

[14]Ding X,Qian Z,Yang S,et al.A direct peak DC-link Boost voltage control strategy in Z-source inverter[C].Proceedings of the 22nd Annual IEEE Applied Power Electronics Conference,2007:648-653.