相关观测值的可靠性研究

（中国地质大学信息工程学院 湖北武汉 430074）

1 引言

可靠性理论由荷兰Baarda[1]教授于1968年最早提出。在一定的假设检验条件下，将平差系统发现、区分不同模型误差的能力称为内部可靠性，将不可发现、不可区分的模型误差对平差结果的影响称为外部可靠性。Baarda 教授给出了可靠性理论的推导方法和计算公式。可靠性理论引起了测量学界的广泛关注，国际上Heck、Pope、Teunissen[2-3]等人和我国李德仁院士对该理论做了深入研究并取得重大发展。可靠性是测量网优化设计和数据质量控制要考虑的重要因素之一，将可靠性理论应用于粗差探测、定位与定值，数据检测与统计分析领域，满足科研和经济建设的需要，取得了良好的效果。

可靠性理论将观测值的多余观测分量ri定义为可靠性指标[4]，多余观测分量越大，该观测值的可靠性越强。然而在观测值相关的情况下，多余观测分量ri的值域已超出[0，1]区间，甚至可能出现负数，内、外部可靠性除了受到ri影响，还有观测值相关程度有关，ri不是唯一影响因素，把ri定义为观测值的可靠性指标是不合适的[5-7]，笔者拟从理论上证明这一结论，论证内、外部可靠性在同一观测位置的统一性和不同观测位置的矛盾性，建议采用一种新的可靠性度量指标，将不同观测位置的内、外部可靠性综合考虑，对新指标的值域和与多余观测分量的关系做说明。新指标是一种统一的指标，值域在[0，1]区间，既适用于独立观测，也适用于相关观测。

2 多余观测分量的值域

2.1 残差理论

设平差的高斯—马尔科夫模型为[8]

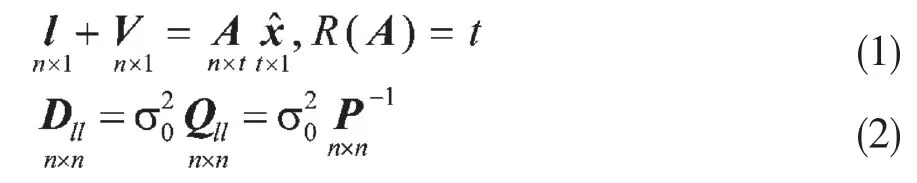
其中l是观测值向量，A是系数阵，秩为t，V是改正数向量，D是协方差阵，Q是协因数阵，P是权阵。由此模型，可以得出

式(4)表示了观测值改正数与观测值误差之间的关系，借助于这个关系式分析观测残差对改正数的影响，形成了可靠性理论。假设第i个观测值含有粗差▽li，它对所有改正数的影响为∶

对其自身观测值的改正数vi的影响为∶

根据Baarda 教授建议定义QVVP的第i个对角线元素为第i个观测值li的多余观测分量，即

考虑到方阵QVVP 为幂等阵，可以证明∶并且ri的值域为[0，1]。

由式(6)可以得出∶某个观测值的粗差仅部分地反映在该观测值的改正数中，ri的值越大，越容易通过检验改正数来发现粗差。因此，将多余观测分量ri作为内部可靠性指标。但这仅仅是针对观测值之间相互独立的情况。

2.2 ri的值域

考察QVVP，有∶

其中，E 为n×n 阶单位阵。令F=A(ATPA)-1AT，G=FP=A (ATPA)-1ATP，这时QVVP 和G 都是对称的正定阵，它们的对角线元素值域都在[0，1]，且考虑到QVV、Qll和Qll都为正定阵，因此观测值权阵P 正定，则有唯一的Cholesky 分解[9]，即P＝HHT，其中H 为n×n 阶非奇异下三角矩阵。

为不失一般性，将要考察的第i个观测安排到第一个观测方程中，将H、HT和F 分块，有

其中 m =n -1。则 G =FHHT，G11=F11H11H11+F1mH11Hm1,当观测值相互独立时，F1m和Hm1为0，G11=1-(QVVP)11∈[0，1]即1-r11∈[0,1]，有r11∈[0,1]；当观测值相关时，G11的值域是F1m和Hm1的函数，无法保证在[0，1]，则r11的值域也无法保证在[0，1]。

以文献[6]和[7]中提到的简单水准网网形A 为例，

G11=2，r11＝1-G11＝-1∉[0，1]。G22＝0.5，r22=0.5∈[0,1]。G33=-0.5，r33=1.5∉[0，1]。从本例子可以看出，相关观测情况下，ri的值域已超越[0，1]，甚至会出现负值。

3 可靠性指标

3.1 内部可靠性指标

观测值的内部可靠性定义为能以一定的检验功效β0，通过显著水平为α0的统计检验可发现的粗差下界值▽0li。根据α0，β0可以确定统计量的非中心化参数δ0。若只含有一个粗差，则该位置内部可靠性为

其中，σ0为单位权中误差，fiT=[0,L,1,0,L,0]为单位化向量，第i个元素为1。记μVi=fiTΡQVVPfi，因此，式(10)可以写成

由式(11)可得出∶在单位权中误差确定的情况下，μVi越小，系统内部可靠性越差；μVi越大，内部可靠性越好。

3.2 外部可靠性指标

外部可靠性是指不可发现、不可区分的模型误差对平差结果的影响程度。

影响向量为

其中▽0s 为参数向量▽s的下界域，将▽0s 分解为表征方向的单位矢量部分s 和表征大小的标量部分▽0s，即▽0s=s▽0(s)，且｜s｜=1。在上式中，我们仅研究外部可靠性大小，不考虑s，▽0s的标量部分▽0(s)即内部可靠性▽0li。定义影响向量长度作为外部可靠性∶

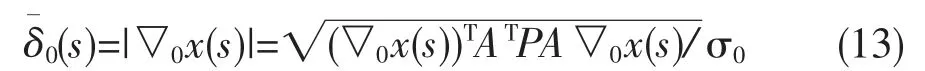
将式(10)和(12)代入(13)中，有

记μi=fiTPQllPfi=fiTPA(ATPA)-1ATPfi，因此，式(14)可以写成

由式(15)可得出∶外部可靠性与单位权中误差无关，而与μi和μVi的比值有关，μi越小，μVi越大，外部可靠性越小；μi越大，μVi越小，外部可靠性越大。

3.3 外部可靠性和内部可靠性的关系

进一步分析式（11）和（15）可以得出

将上式所得结果定义为第i个观测值li的可靠比，记作ηi，可进一步研究∶

(1)对于确定的观测值li，外部可靠性与内部可靠性是统一的，即内、外部可靠性成固定比例，为定值，值的大小取决于观测值的精度和网的几何图形条件，已知内、外部可靠性中一个值时，可以根据可靠比求出另一值。

(2)不同观测值之间，由于精度和几何图形条件不同，可靠比不同，精度和几何图形条件越好，可靠比越小；精度和几何图形条件越差，可靠比越大。内、外部可靠性无法统一，极有可能出现按照内部可靠性定义出现的最弱处与按照外部可靠性定义出现的最弱处矛盾，可见，单纯依靠内、外部可靠性定义无法客观评估观测值的可靠性，需要引入能够克服这一缺陷，综合表示可靠性的新指标。

(3)实际应用中，可在获得观测值之前，根据所设计的平差图形计算出可靠比，初步用于网形优化设计和测量质量控制。

应当指出，文献[5]中提出外部可靠性λxi与内部可靠性λli相差一个常数，即

λxi=λli-λ0

其中λ0是一定概率条件下的非中心参数。事实上，内外部可靠性之差并不是常数，而与观测值的精度和该观测值所处的图形条件相关，这点将在算例中体现。

3.4 内外部可靠性与多余观测分量的关系

当观测值相互独立时，Qll和P 都是对角阵，μVi=Piiri，μli=Pii，分别代入式(10)和式(14)中，有∶

由上式可知∶μli与μVi都与ri有关，ri可以统一表示内部可靠性▽0li和外部可靠性。但当观测值相关时，μli与μVi都与ri没有确定函数关系，ri无法统一表示▽0li和，再结合本文2.2 节关于ri值域的证明，可以看出，当观测值相关时，ri已不能作为表征可靠性的指标，需要提出一种新指标。

文献[6]和[7]建议采用Ri=qiifiTPQVVPfi=qiiμVi定义可靠性指标，Ri越大，可靠性越强，Ri越小，可靠性越弱。应当指出的是0≤Ri≤QiiPii，值域不在[0，1]，且采用该指标定义的内外部可靠性矛盾，本文将在第5 节的算例中证明。

4 一种新的可靠性指标

4.1 定义

将式(3)代入式(15)，记μli___=fiTPQllPfi，有

笔者建议定义一种新的可靠性指标，即定义

为系统在第i个观测位置的可靠性度量，φi为比值，无量纲。将式(20)分别代入式(11)、(15)和(16)，有

可以看出φi越大，内部可靠性▽0li越小，外部可靠性越小，由于外部可靠性幅度大于内部可靠性，可靠比ηi越小，可靠性越好；φi越小，可靠性越差。

4.2 φi的值域

由式(3)结合定义，得∶μli=μVi+μi。考察式(20)，有

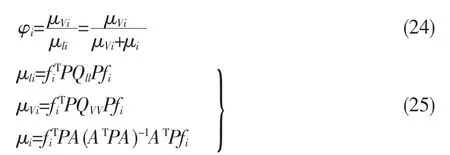
式(25)中三个量均为二次型，各设为

其中行向量n 维xT为fiTP，n 维列向量x 为Pfi，x1，x2，L，xn为P的第i行元素pi1，pi2，L，pin，M分别为Qll、QVV和A(ATPA)-1AT。因为Qll、QVV和A(ATPA)-1AT均为正定阵，所以对于任何x≠0，都有μli＞0、μi＞0、μVi＞0 恒成立，所以有φi∈[0,1]，当观测值li为完全必要观测时，φi=0；当观测值li为完全多余观测时，φi=1。

4.3 可靠性指标φi 与多余观测分量ri的关系

为研究新指标是否适合观测值相互独立的情况，现考察可靠性指标φi与多余观测分量ri的关系。为不失一般性，将要考察的第i个观测安排到第一个观测方程中，第二组为剩余的全部观测值。相应的方差—协方差矩阵分解为[4，5]

由分块矩阵求逆公式可得∶

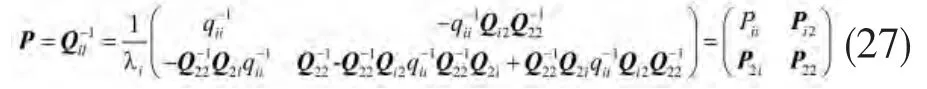
式中∶

由于P是正定阵，0≤λi＜1。按上述观测值的分组方法，可靠性矩阵QVVP 也可以被分解，有

几何条件矩阵的对角元，即观测值li的多余观测分量ri为

根据φi和ri的定义，可导出如下关系式∶

式(17)表明，可靠性指标φi和多余观测分量ri一般是不相等的。下面就一些特殊情况进行进一步讨论∶

(1)当λi=1时，即观测值相互独立，Qi2=0，φi=ri；

(2)当0≤λi＜1，且li为完全必要观测值时，ri=0，可以证明∶Qi2Q-122QV22Q-122Q2i=Q2iQ-122QVi2。从而导出φi=0；当0≤λi＜1，且li为完全多余观测值时，ri=1，QV21=Q2i，当Qi2Q-122Q2i=Qi2Q-122QV22Q-122Q2i时，φi取得最大值1。

根据φi与ri关系，进一步考察式(21)和(22)，当观测值相互独立时，φi=ri，μli=Pii，式(21)和(22)变成式(17)和(18)。即新指标φi既适用于观测值相关的情况，也适用于观测值相互独立的情况，实现了内、外部可靠性的统一表示。

4.4 关于可靠性指标的进一步思考

(1) μli、μVi、μi和σ0=VTPV/r 都是正定二次型，分别表征了观测值误差、平差误差、不可发现不可区分的模型误差和已知的模型误差，进一步分析得∶观测值经过平差后，在改正数的修正下，产生改正值；观测值的误差在经过改正数修正后，不可发现不可区分的模型误差残存在改正值中。当然，改正数也是有误差的，即平差误差，因此观测值误差由平差误差和不可发现不可区分的模型误差构成。

(2)由式(11)、(15)和(16)可知，内部可靠性是已知的模型误差与平差误差的比值，即已知误差对于平差结果的影响，具体表现为可发现的粗差下界值；外部可靠性是不可发现不可区分的模型误差与平差误差的比值，即不可发现不可区分的模型误差对平差结果的影响。可靠比ηi是不可发现不可区分的模型误差与已知模型误差的比值。

(3)进一步考察式(20)可知，新的可靠性指标φi表征了平差误差与观测值误差的比值，反映了平差误差所占观测值误差的比例，该比例越大，平差模型越接近真实情况，残余误差（即不可发现不可区分的模型误差）越小，系统可靠性越高，反之亦然。φi值域必为[0，1]，当平差误差为0时，即不用平差，该观测值为完全必要观测，φi=0；当平差误差为观测值误差时，该观测值为完全多余观测，φi=1。

(4)由式(31)可知∶新指标φi与多余观测分量ri在观测值相关时不相等，之间的差值由第i个观测值与其他观测值的相关程度决定，因此，m=r（多余观测数）。

5 算例与分析

下面通过三个算例计算相关指标来说明或验证上述结论。

【例1】 利用文献[5]中[例3]的GPS 单频相位差分观测实验计算有关指标见表1。

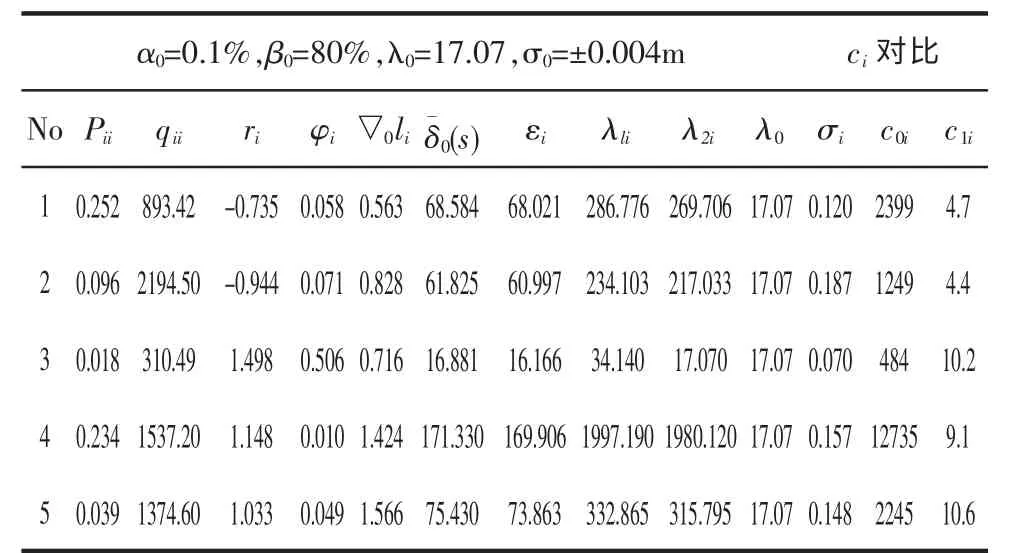
表1 GPS 单频相位差分算例的有关可靠性指标比较

从表1的数值可以看出∶

(1) ri值域不在[0，1]区间，变化幅度非常大，甚至出现负值，且ri与▽0li、的大小没有表现出一致性，可见相关观测情况下，ri已无法再作为可靠性指标；φi值域在[0，1]区间，按照φi分析，网中可靠性最弱的位置在l4处，φ4=0.01 最小；可靠性最强的位置在l3处，φ3=0.513 最大。

(2) 按照内部可靠性指标，l5处最弱，l1处最强；而按照外部可靠性指标，l4处最弱，l3处最强，可见内、外部可靠性出现了不统一。

(4)外部可靠性与内部可靠性的差值εi随着观测位置的不同而发生变化，文献[5]中说明内外部可靠性差值为定值λ0（一定概率条件下的非中心参数），这种说法的合理性值得商榷。

(5)按照文献[5]中内部可靠性计算得出的可控性数值非常大，而本文产生的结果都在10 倍以内，文献[5]中内部可靠性定义值得商榷。

【例2】 利用文献[6]中的GPS 三次差分观测值数据进一步计算有关指标，见表2。Ri为文献[6]中定义的可靠性指标，最后两列的▽0li和为以l1观测值内外可靠性为基准，其他观测位置可靠性的比值，用以更明了的表示各个位置可靠性强弱。

表2 文献[6]中GPS 算例数据的进一步分析

从表2的数值可以看出∶

(1)该算例的特点是各个观测位置权值、内部可靠性都没有明显差异，外部可靠性差异较大。十四个观测值可靠比ηi各不相同，这是由于ηi由精度和几何图形条件决定，精度和几何图形条件越差，ηi越大；精度和几何图形条件越好，ηi越小。l14处，η14=18.974 最小；l5处，η5=41.110 最大。所以网中精度和几何图形条件最好的在l14处，最差的在l5处。φi值域在[0，1]区间，按照φi分析，网中可靠性最弱的位置在l5处，φ5=0.492 最小；最强的位置在l14处，φ5=0.820 最大。φi与ηi表现出相反性。

(2)按照文献[6]定义的可靠性指标Ri=qiiμVi值域不在[0，1]，无法直观显示出可靠性强弱。Ri最大在l11处，R11=1.639；最小在l7处，R7=0.940。由于该算例qii的值没有变化，因此Ri与μVi正相关。而▽0li与μVi反相关，所以Ri与▽0li反相关，▽0li最小在l11处，▽0l11=0.377；最大在l7处，▽0l7=0.498，而最大在l5处，()5=41.110，最小在l14处，()14=18.974。可见Ri只能部分地表征内部可靠性，而无法表征外部可靠性，不能将两者综合考虑，所以该值定义为可靠性度量指标的合理性值得商榷。

(3)按照内部可靠性指标，l7处最弱，▽0l7=0.498，l11处最强，▽0l11=0.377；而按照外部可靠性指标，l5处最弱，()5=41.110，l14处最强，()14=18.974。可见内、外部可靠性出现了不统一。综合l5、l7的可靠比ηi、μi、μVi可以看出，l5虽然内部可靠性稍强于l7，但外部可靠性()5=17.328 大出()7=13.222 很多，即l5处发现粗差的下界值较小，但平差误差占观测值误差的比例较小，大量不可发现不可区分的模型误差存在，因此综合衡量考察φi，网中可靠性最弱的位置在l5处。同理，可靠性最强的位置在l14处。

【例3】 构建一组水准网的模拟的相关观测值进一步阐述上述结论。图1为一水准网，A 为已知水准点，高差观测数n=5，必要观测数t=3，多余观测数为r=n-t=2，路线上方的数字表示编号。权阵P 有如下形式∶

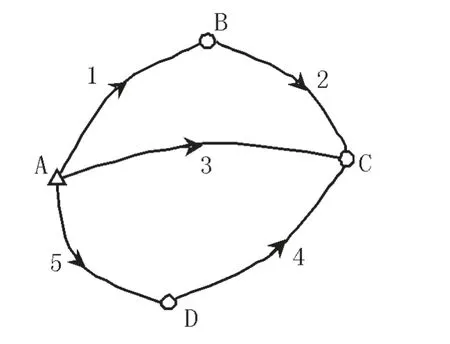
图1 水准网示意图

计算有关可靠性指标，数值列在表3中。

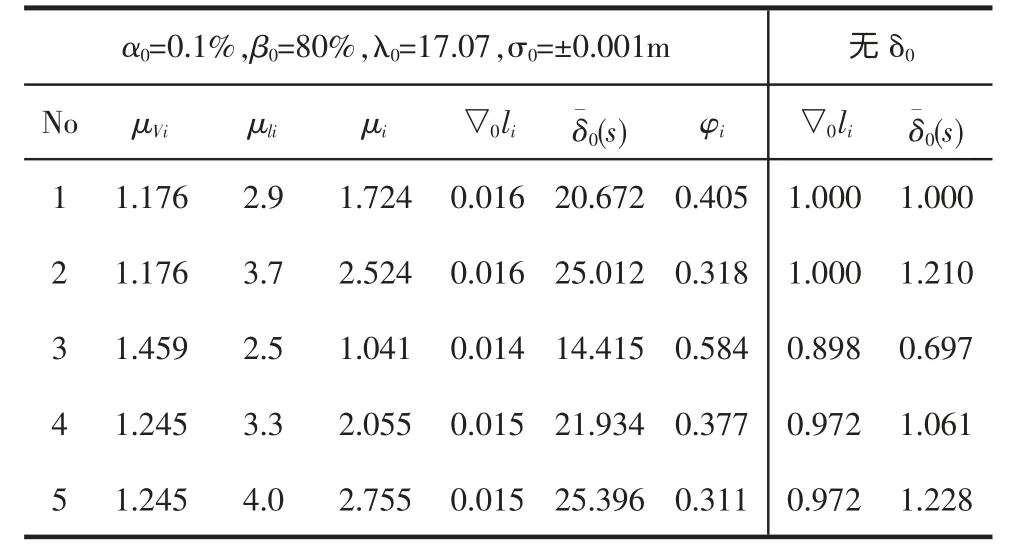
表3 水准网算例数据的可靠性指标

从表3的数值可以看出∶φi值域在[0，1]区间，按照φi分析，网中可靠性最弱的位置在l5处，φ5=0.311 最小；最强的位置在l3处，φ3=0.584 最大。

6 结束语

(1)本文证明了在观测值相关的情况下，多余观测分量ri值域不为[0，1]且不能用于度量可靠性。

(2)本文论证了内、外部可靠性的辨证统一性，即对于确定的观测值，内、外部可靠性成固定比例，该比例大小取决于观测值的精度和网的几何图形条件；不同观测值之间，由于精度和几何图形条件不同，内、外部可靠性无法统一，极有可能出现按照内部可靠性定义出现的最弱处与按照外部可靠性定义出现的最弱处矛盾。

(3) 本文建议采用一种新的可靠性指标φi=μVi/μli，将内、外部可靠性综合表示，φi∈[0，1]，φi越大，可靠性越好，φi越小，可靠性越差。

(4)本文讨论了φi与多余观测分量ri的关系，当观测值相互独立时，φi＝ri；当观测值相关时，φi与ri的关系不确定。

[1]Baarda W.A Testing Procedure for Use in Geodetic Networks[J].Neth Geod.Comm，1968，2(5).

[2]Teunissen P J G.Inteiding Toetsings Theorie [J].Faculty of Geodetic Engin -eering，The Netherlands:Delft Univ.of Technology，1989.

[3]Teunissen P J G.Quality Control in Geodetic Networks[J].Optimization and Design of Geodetic Networks，1984，526-547.

[4]李德仁，袁修孝.误差处理与可靠性理论[M].武汉:武汉大学出版社，2002:98-104.

[5]欧吉坤.相关观测情况的可靠性研究 [J].测绘学报，1999，28(3):189-194.

[6]王金岭，陈永奇.论观测值的可靠性度量[J].测绘学报，1994，23(4):252-257.

[7]黄声享，王金岭.多余观测分量与可靠性度量指标研究[J].武汉测绘科技大学学报，1997，22(2):114-118.

[8]武汉大学测绘学院测量平差学科组.误差理论与测量平差基础[M].武汉:武汉大学出版社，2003:102-104.

[9]方保镕，周继东，李医民.矩阵论[M].北京:清华大学出版社，2004:291-300.

[10]施闯，刘经南.基于相关分析的粗差理论[J].武汉测绘科技大学学报，1998，23(1):05-09.