炉法炭黑结构参数对橡胶电性能的影响
赵志正 编译
(西北橡胶塑料研究设计院, 陕西 咸阳 712023)
把不同牌号的炭黑加入橡胶,提高炭黑在胶料中的含量,这样,就会引起胶料和硫化胶电性能、塑弹性、硫化特性、弹性强度性能发生变化。能使橡胶电性能发生重大变化的因素,是向胶料中添加特种牌号的炭黑,即具有中等分散性及高结构的炭黑[乙炔炭黑(П367Э)];或者是高分散性及中等结构的炭黑(УМ66、УМ76、УМ85),或者是高分散性和高结构的炭黑(П267Э)。与此同时,将活性较低的炭黑(П803、П705等)加入胶料,无论添加多少,也不会引起橡胶电性能发生明显的变化,尽管这些牌号的炭黑的电性能参数,跟以上所述的炭黑并没有什么不同之外。
橡胶电性能的高低取决于多种因素:生胶的品种、炭黑粒子表面的纯洁度和孔隙度、配合工艺因素(例如增塑剂或者表面活性剂的含量)等。在改变橡胶电性能方面作出主要贡献的是炭黑的含量、炭黑粒子的尺寸(分散性)与结构性。这些因素会同时产生作用。因此,要确定每一个因素对改变电性能的贡献的大小,是十分复杂的。能够把橡胶加工成导电橡胶的不同牌号的炭黑,在橡胶内的含有量上下要相差好几倍。即使橡胶中不同炭黑的结构度与分散性非常接近,其体积电阻率也相差好几个数量级。
由此,必须寻找出一个综合性的指标,该指标在兼顾炭黑的物理化学特性的同时,还适用于制造高导电橡胶。
该文作者认为,可以把橡胶中炭黑的原生聚集体之间接触点的数量比值(KK)作为这一指标,它可以同时兼顾炭黑的含量、分散性及结构性。可以用一种模型来计算接触点的数量,该模型的基础是表达了炭黑的特性,这些特性又是通过对炭黑进行综合分析后确定的。这种方法的实质是,用高温裂解的碳对炭黑原生聚集体的内部空隙进行充填,并周期性控制这一充填过程。通过测定最终填充度接近于“零”时的质量和吸附表面来实现周期性控制。这里就提出了炭黑的吸附比表面积(Aа)和外比表面积(Aв)这二个概念,当然还包括了最终填充度(SK)。这个最终填充度与高温裂解碳的质量相等。高温裂解碳又是充填聚集体内部空隙所必需的,它的质量归属于炭黑的初始称量。应当指出,用这种方法测出的Aв实际上是跟炭黑粒子的几何比表面积相吻合的[4]。由于高温裂解的碳的密度与炭黑的密度几乎是一样的(ρ=1800 kg/M3),因此最终填充度(SK)就是炭黑聚集体中,粒子之间的孔隙容积(VП)与粒子的体积(VЧ)之比。

假如说,构成炭黑原生聚集体的所有粒子都是球形的,其直径(DЧ)相同,那么它们的直径、容积(VЧ)以及比粒子数(NЧ)都是炭黑的质量单位,可以利用下式进行计算:

式中,DЧ—粒子的直径/nm;Aв—外比表面积/(m2·g-1);ρ—炭黑密度/(g·cm-3)。

式中:VЧ—粒子的体积/m3;DЧ—粒子的直径/Hm;m—质量/g;ρ—炭黑密度/(kg·m-3);NЧ—按质量单位计的比粒子数。
正如研究所指出的那样[5],大多数炉法炭黑聚集体都是由球形粒子构成的线形和串状的物质。为了简化计算,假设最初的炭黑聚集体是球形的,并由相同的粒子数(Z)构成。这样,橡胶中聚集体的数量Na可用下式表示:

式中:M—炭黑的含量/g。
在相同直径的球体被充填的条件下,胶料的总体积VS(胶料中所有组份体积的总和)与炭黑球形体积Vа(此处为炭黑原生接触聚集体)之比,跟每个球体(聚集体)与相邻球体接触点数量(n)之间的关系,可以用下式计算:

VS/Vа是橡胶中炭黑原生聚集体的体积分率。为了简化起见,用C表示VS/Vа,经过一系列转换得到以下二次方程式
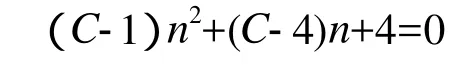
式中的根n—每个炭黑原生聚集体与相邻聚集体的接触点的数量,可用下式计算:
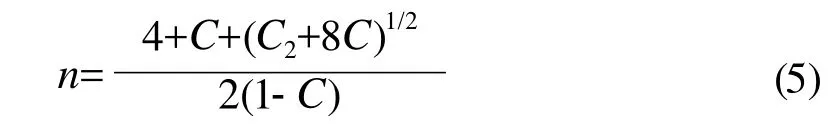
炭黑聚集体之间接触为的总量为:

式中:Z—炭黑聚集体内粒子的数量。
根据文献报导,可以确认Z值约为100~400个粒子。假设所研究的所有炭黑品种Z=100,则在单位质量中聚集体的比例为:

为了检验关于接触点数量与硫化胶电性能之间的相关性的假设是否可靠,曾从卡博特公司的产品目录中找到了含有50质量份不同牌号炭黑的硫化胶体积电阻率(ρV)的数据。按照公式(5)确定每个聚集体与相邻聚集体的接触点数量时,曾获得下列典型参数:
● 胶料的总体积VS=142·10-6(包括胶料中所有配合剂的总的体积);
● 炭黑粒子的体积(VЧ=50/1.8);
● 炭黑聚集体孔隙的容积(Vn=VЧ·SK);
● 炭黑聚集体的体积[Vа=VЧ+Vn=VЧ·(1+SK)];
● 在总体积中炭黑聚集体的体积份(C=Vа/VS)。
计算聚集体之间接触点的数量所必需的实验与统计数据见表1所示。
KK这一指标可以用来表示橡胶中聚集体跟相邻聚集体之间接触点的总的数量。为了对计算结果进行比较和分析,使用有比例的指标比较方便。它适合于所研究的对象——单位体积中接触点数量的比值。
在图1中绘出了体积电阻率与炭黑聚集体之间比接触点数的对数关系曲线。看来,尽管有许多假设可以被采纳,坐标平面上的许多点的近旁有一条有走向的曲线,这条曲线可以用幂方程式lgρV=8,16·105,表示,也就是说lgρV=f(Kv)关系曲线具有明显的规律性。这极有可能是由以下原因造成的:引数Kv本身就同时包含了炭黑的含量(M)以及用NЧ表示的炭黑的分散性,当然,也包括了由聚集体之间的接触点数(n)表示的结构度。

图1 体积电阻率与不同牌号炭黑聚集体之间比接触点数的对数关系曲线
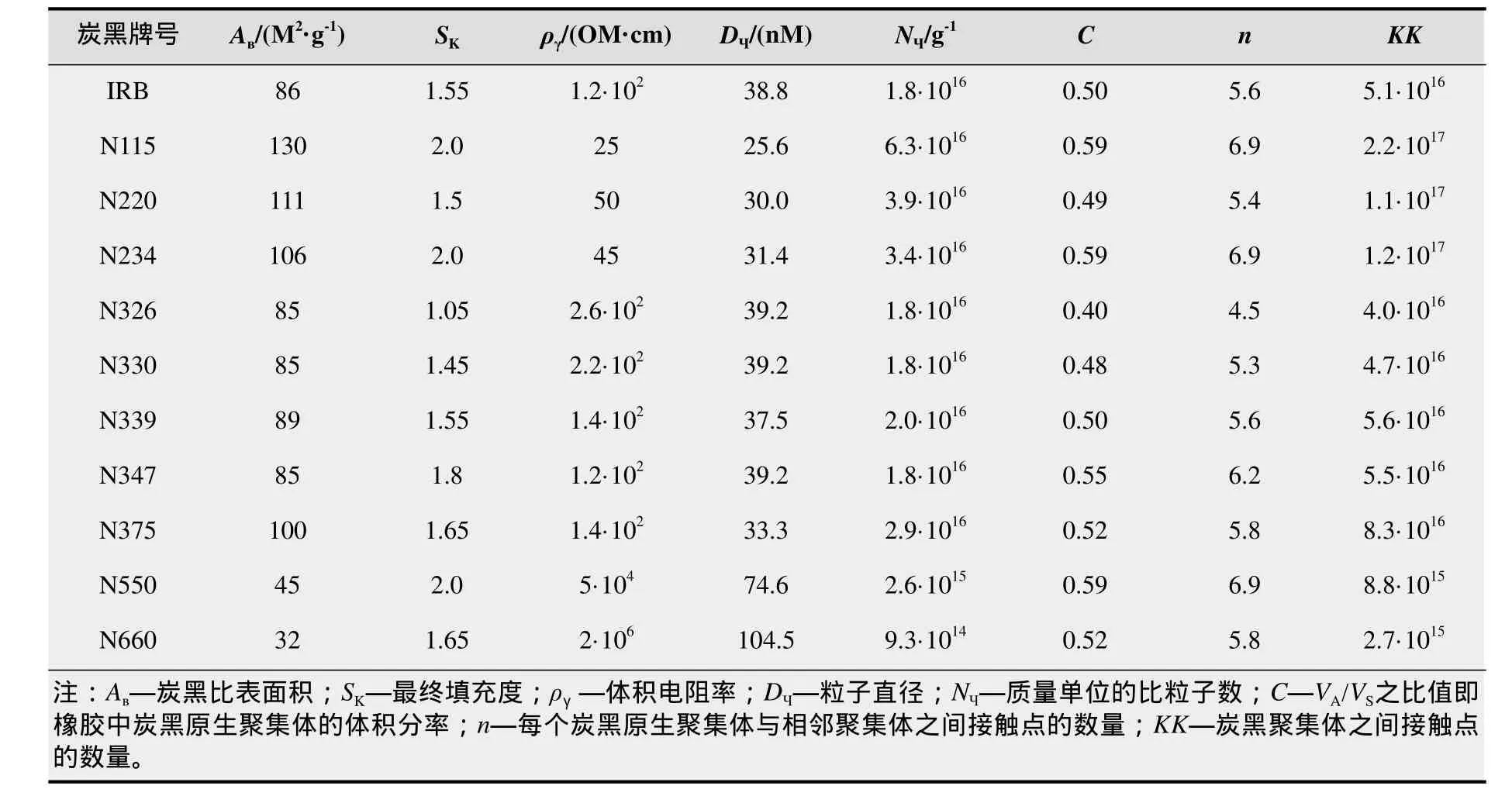
表1 不同牌号炉法炭黑原生聚集体之间接触点数量的实验与统计数据
实际上把具备ρv<106OM·cm(104OM·M)条件的橡胶都归于导电橡胶的范畴。对所得曲线的分析表明,在所研究的方案中,当Kv>2.4·1013时,这一条件能得到保证。在表1中列出的所有炭黑牌号(N660炭黑除外)都能满足这个条件。在所有被研究的炭黑牌号中比粒子数N660炭黑最小,分别为9.3·1014及Kv=1.9·1013。使用这一牌号的炭黑也许能制备导电橡胶,但必须将炭黑的含量增加到10质量份,在这种情况下Kv的值才能够达到3·1013。然而,对于如П803这样的炭黑来说,填充量为50质量份,NЧ=9.7·1013,Kv=2.2·1012。在这种情况下,要使NЧ提高一个数量级(无论橡胶中含有多少П803炭黑)都是不可能的。也就是说,不可能制得ρv<104OM·M的橡胶。
为了对所推荐的模型进行检验,测定了分别含有20、30、40和60质量份УМ(76)炭黑的天然橡胶的ρv。该牌号炭黑的Aв=135M2/g,SK=1.65。相应的点坐标实际上都与方程式lgρv=8.16·105Kv-0.36相吻合(参见图1)。
综上所述,可以把炭黑聚集体之间接触点数量的比值(Kv)(即分数性与结构度相结合的参数)用来对橡胶的导电性能进行预测和分析。有三种因素会使指标(ργ)发生变化,其中,分散性的作用最大。这是因为填充剂的分散性在质量单位上决定了聚集体接触点数量的比值(NЧ)。
[1]Корнев А.Е. Овсянников Н.Я.//Вестник МИТХТ. 2009. Т.4. No 2. C. 3.
[2]Крикоров В.С., Колмакова Л.А. Электропроводящие полимерные материалы. М.:Энергоатомиздат, 1984. -176 c.
[3]Песин О.Ю., Эстрин Р.И. // Химия твердого топлива. 1997. No 3. C.14.
[4]Печуро. Н.С, Песин О.Ю. Эсмрин Р.N. и гр//тамже. 1977. No 5. С.90.
[5]Орлов В.Ю., Комаров А.М., Ляпина Л.А Производство и использование технического углерода для резин.Ярославль:Изд-во Александр Рутман, 2002. - 512 c.
[6]Эсмрин Р.И. // Наука и технология углеводородов. 2000. No 4(11), C. 92.
[7]Ильин А.Н., Цыганкова Э.И., Гришин Б.С. и др. // Пути развития промышленности технического утлерода:Сб. научн. тр. М.:НИИШП, 1976. C.28.
[8]Горюнов Г.Л., Суровикин В.Ф. // Достижения в области производства и применения техничского углерода: Сб.научн. тр. М.:ЦНИИТЭнефтехим, 1980. C.25.
[9]Суровикин В.Ф., Горюнов Г.Л., Шуплецов В.Г. //Там же. 1980. C. 40.
[10]Аникеев И.В., Аникеев В.Н., Никиmин Ю.Н.//Тез. докл. ХV Межд. научно-практ. конф.《Резиновая промышленность.Сырье, материалы, технологин》(Москва, 2009). C.204.
[11]Эсмрин Р.И //《КИР》2010. No.3 C24-26.

