基于导频的三维信道估计

于国庆，段红光

(重庆邮电大学通信与信息工程学院，重庆400065)

为了方便相干检测，已知的参考信号(导频符号)一般在发射端被插入到发射信号中。对于PACE，导频信号被等间距地放置在发射信号流中。如果放置的间隔充分接近并满足抽样定理，整个数据序列的信道响应可以通过插值得到。对于OFDM系统，接收到的信号在时域和频域是相关的。应用于OFDM系统，PACE通过在时域和频域分散配置导频，从而扩展到时域和空域，在时域和频域抽样，通过插值［1］进行二维信道估计。由于实现了估计精度和所需导频开销的良好平衡，2D PACE被广泛选为无线通信标准，如地面数字视频广播(DVB－T)［2］、第三代移动通信系统。

采用多个发射和接收天线的系统称为多输入多输出(MIMO)系统，能使系统容量大大增加，并且是3G系统的一个组成部分。然而，因为发射天线互不相关，使得发射导频符号所消耗的资源随着发射天线数的增加而增加。从而，MIMO的优势会由于导频开销的增加而被抵消，尤其是发射天线数很大时。

在基站发射机安装在屋顶的MIMO－OFDM的下行链路中，波的离开角度包含了一个比较小的角度扩展，从而使发射天线空间相关。天线间的空间相关性［3］被用来提高信道估计的精度，本文采用另一种方法:利用空间相关性来减少导频开销。通过仅在所选发射天线子集插入导频符号，所有发射天线的信道响应通过插值被保留。对MIMO－OFDM系统，在时域和频域二次抽样而扩展到空域，即三维的PACE。

1 系统/信道模型

考虑每帧具有L个OFDM符号、Nc个子载波的OFDM系统。OFDM符号l、子载波n的发射信号矢量由具有Nt个元素天线阵列发射，表示为 xn，l= ［，…，］T，总的发射功率为。OFDM 调制是一个Nc点的逆DFT(IDFT)变换，伴随着长度为Ncp的循环前缀。发射信号通过一个Nt×1维的多径衰落信道传播，空间信道响应为。假设在时域和频域是完全正交的，接收符号表示为

式中:zn，l代表加性高斯白噪声(AWGN)，它的均值为0、方差为N0。假设归一化平均信道增益为，由天线μ接收的每个符号的平均信噪比为。

接收信号式(1)应用于配有1根接收天线的移动接收器，可扩展到多个接收天线处理。如果MIMO－OFDM系统中接收天线不相关，每根接收天线的信道估计将独立进行，并直接应用。当接收天线相关时，信道估计的精度可以通过对接收天线接收到的训练序列利用空间平滑进行改进。OFDM符号块l的矢量符号可以表示为

维数为Nc×NTNc的二维发射信号矩阵由频域和空域发射符号组成，表示为Xl=diag［，…，］。同样地，维数为NTNc×1的二维矩阵CTF(信道转移函数)描述为。最后，维数为Nc×1 的噪声矢量表示为 zl= ［z1，l，…，zNc，l］T。

接收信号由L个OFDM符号组成，即

式中:X=diag［X1，…，XL］;h=;z=［，…，］T。

信道模型:式(1)中维数为NT×1的矢量hn，l表示了信道转移函数(CTF)，hn，l第μ列描述了发射天线μ和接收器之间的CTF，表示为

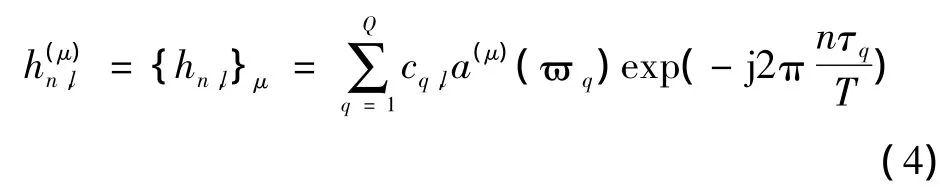
式中:T=NcTsp1，Tsp1代表抽样间隔;cq，l为信道抽头q的复数权重，1≤q≤Q;φq为离开基站的角度(AOD);τq为到达时延。由于终端移动产生多普勒效应，对于天线间隔d为均匀线性阵(ULA)，天线μ的阵列响应为

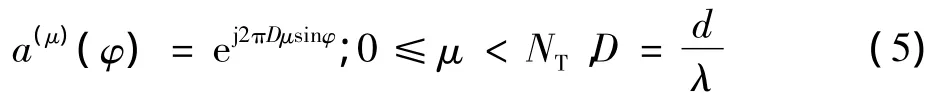
式中:d代表天线元素间距;λ为载波波长。

信道的相关性:第二阶段的统计由在时域、频域和空域独立的三维相关函数确定，即

一般假设对于所有的Q信道抽头，时间相关Rt［Δl］是相同的，因此Rt［Δl］与信道抽头q无关，另一方面，测量表明空间相关Rs，q［Δμ］与信道抽头q有关。从而，三维的相关函数可以分解为Rt［Δl］和Rf，s［Δn，Δμ］。

假设基站安装在屋顶上，AOD分布在具有角度扩展为θ的平均AODφ 附近，即φq∈［φ－θ，φ+θ］，∀q，如图1所示，θ导致发射天线之间空间相关。

图1 空间信道模型，基站处的AOD分布在角度扩展为θ的平均AODΦ附近

2 基于训练序列的3D信道估计

PACE对噪声信道响应抽样并通过插值［1］的方式获得整个序列的信道估计。对于常规的二维PACE，已知训练序列符号按等间距插入到时域、频域，间隔分别为Dt，Df，然而以前的MIMO－OFDM信道估计利用空间相关性来提高信道估计［3］的精度，对于3D PACE，空间相关性被用来减少导频开销。通过允许空域导频间隔为Ds，导频符号仅插入到发射天线的一个子集，所有发射天线的信道响应通过在空间插值得到。

总数为NP=NP，s×NP，f×NP，t的导频符号分布在空域、频域和时域。一个常规的三维网格结构可以唯一地描述为

为了获得所有NT发射天线的信道估计，属于不同发射天线的导频符号分别在时域或频域正交。为了达到这个目的，一种方法是利用条件mod(dsf，Df)≠0或mod(dst，Dt)≠0，使不同天线元素的导频在频域分开。这就为式(3)中三维的CTFh提供了一个受噪声干扰的二次采样版本，避免了属于不同天线的导频干扰。注意，也可能有其他正交分离导频符号的方法，但是会导致更高的复杂性或至少相同的导频开销。然而，该3D PACE也可以推广其他方案，如相移导频序列［4］，将二维扩展到三维。

并不是所有的NP=NP，s×NP，f×NP，t导频符号都可能用于信道估计。而某个子载波的CTF估计可能被限制在导频符号的一个子集，时域Mt≤NP，t，频域Mf≤NP，t，空域Ms≤NP，t。接收到的维数为M×1的训练序列为=+，其中M=MtMfMs，接收到的训练序列是受到噪声干扰的三维CTFh的二次抽样版本。

2.1 维纳插值滤波器的推导

由~h表示的对三维CTFh的估计是通过基于三维插值的最小均方误差得到的。维纳插值滤波器(WIF)是由一个FIR滤波器w(n)来实现的，抽头为M=MtMfMs。对子载波n，OFDM符号l，发射天线μ的CTF估计表示为

矢量n=［μ，n，l］T指被估计的符号。利用已知的接收训练序列，维纳插值滤波器，期望响应和滤波器实际输出之间的最小均方误差。

2.2 与模型不匹配的维纳插值滤波器

与模型不匹配的维纳插值滤波器的特征在于所假设的用来生成滤波器系数的相关函数R'与实际的R不同。与模型不匹配的WIF的优点是，它可以基于最坏传播条件的先验知识计算滤波器系数。为了生成滤波器系数，假设非匹配的三维相关函数为

然后在维纳—霍夫方程中插入R'替代真正的相关系数R而得到滤波系数。根据文献［5］，对于二维的PACE，在频域和时域非匹配的相关函数，是假设功率延迟和多普勒功率都是均匀分布的的前提下产生的，在［0，τmax］和［－fD，max，fD，max］内是非 0 的。此外，为了计算式(8)，需要已知滤波器输入端的平均。

在空域，发射天线μ和μ+Δμ之间的相关性表示为

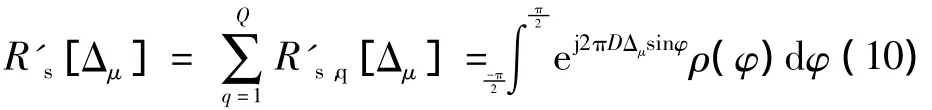
式中:ρ(φ)代表AOD角度分布的概率密度函数。当实际的频率空间相关性不能被分为空域Rs和频域Rf时，与模型不匹配的3D PACE的性能将有所下降。这跟时域和频域相关性函数一般可分开的2D PACE形成鲜明的对比。这表明，由于模型不匹配产生的性能损失，3D PACE大于2D PACE。

2.3 空间抽样定理

2D PACE抽样定理为时域和频域的导频间隔提供了上限。应用到空域，抽样定理确定了空域导频间隔的最大值Ds。在天线μ=Ds按间隔Ds周期地插入导频信号，按速率进行空间抽样，，二次抽样矩阵响应表示为

式中:「x⏋代表向上取整。由于(φ)是以2π为周期的周期函数，空间混叠被分开，其中k为任意的整数。对于参考空间信道模型，离开电磁波包含了一个在平均AODφ附近的角度展θ，在一定范围内，角度分布Δ=sinφ为非零的。

抽样定理表明对于给定的空间内的无限数目的导频，即－∞≤≤∞ ，所有天线的阵列响应，即式(5)中的a(μ)(φ)能被理想重建。如果Δ =sinφ角度分布不发生混叠，当空域导频符号数目被限制在内时，空间抽样定理给出了最大Ds的一个非对称上限。由于实际导频数目是有限的，所以实际上Ds的值应该比理论值小。由不混叠的条件和三角加法定理，可以推导出空间导频间隔的上限，即

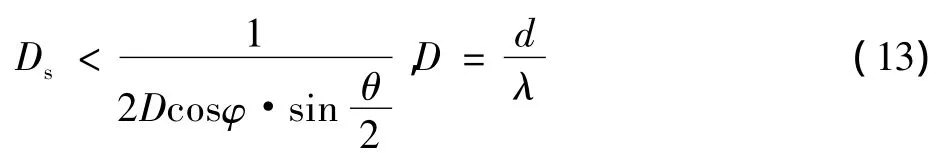
3 MSE分析

任意维数为1×M的3D估计器的MSE的一般表达式为

一个具有4根发射天线的MIMO－OFDM系统，元素间隔为=0.5，以IST－WINNER2参数为基础。一帧包括L=12个OFDM符号，每个OFDM符号有Nc=1 024个子载波，循环前缀的长度为TCP=128·Tsp1。信号带宽为B=40MHz，从而得到采样周期为，一个子载波间隔为≈39 kHz。OFDM符号间隔为Tsym=35.97μs，其中循环前缀为TCP=3.2μs。假设在城市环境中，终端的移动速度为50 km/h。载波频率为5 GHz，转化为归一化最大多普勒频率为fD，maxTsym≤0.006 7。WINNER project规定典型的城市信道环境的角度扩展为35°。

对于时域和频域的导频间隔，选择Dt=9，Df=6。对于空域导频间隔，由采样定理可知，Ds≤3。为了允许过采样，选择Ds={1，2}，此外，设l0=1 ，μ0=1 ，n0=1。通过设置dsf=1和dst=0，使不同发射天线的导频正交。信道估计单元由WIF执行，滤波器系数为:Mt=2，Mf=16，Ms=。

图2和图3绘制了3D PACE的信噪比MSE图，把没有利用空间相关性的传统2D PACE用作对比。图2展示了Ds=1，即导频在所有天线上发射的3D PACE的结果。在这种情况下，2D PACE和3D PACE使用相同的网格结果，具有相同的导频开销。与2D PACE相比，3D PACE利用了空间相关性，以此来提高信道估计的准确性。但是，当使用非匹配模式的估计器时，3D PACE相对2D PACE的性能增益减小，在高信噪比时尤其严重。造成匹配WIF和非匹配WIF这种相当大差异的原因是，空间频域相关函数的特性Rfs［Δμ，Δn］，它是导致与非匹配 WIFR'f［Δn］·R's［Δμ］重大不同的原因。另一方面，对于2D PACE，时域频域相关函数R2D［Δn，Δl］能够被分解为时域和频域成分Rf［Δn］ = ∑q Rf，q［Δn］和Rt［Δl］，这就意味着匹配WIF和非匹配WIF能够密切接近。图3展示了Ds=2的3D PACE空间插值结果。对于菱形网格结构，3D PACE的性能和2D PACE很接近，而3D PACE的导频数目仅仅是2D PACE导频数目的一半。因此，3D PACE可以在不牺牲性能的情况下，使导频开销减少一半。对于矩形网格结构，在高信噪比时，将出现平底效应，即使是完全匹配WIF的情况。这种效应主要是因为边缘效应造成的:当导频只在天线1和天线3上发射时，对于天线4的估计是通过插值得到的，这将导致估计误差显著增加。因此，3D导频模式对提高信道估计精度具有显著的影响。

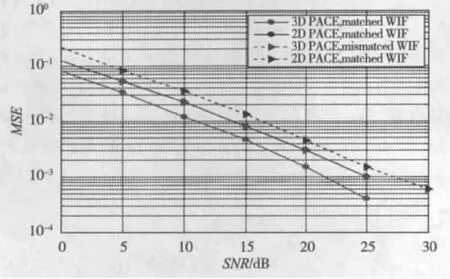
图2 3D PACE，D s=1情况下的MSE图

图3 3D PACE，D s=2情况下的MSE图

4 结束语

三维导频设计通过插值将MIMO－OFDM信道估计从时域、频域扩展到空域。合适的网格结构能够最佳地利用空间相关性。如果发射天线阵列具有相关性，通过在发射天线使用插值原理，可以在不牺牲性能的情况下大大减少导频开销，提高信道估计精度。

［1］ OHER P H.TCM on frequency selective land－mobile fading channels［C］//Proc.5th Tirrenia InternationalWorkshop on Digital Communications.Tirrenia，Italy:Citeseer Press，1991:317－328.

［2］ ETSI EN 300 744，V 1.4.1(2001－01)，Digital video broadcasting(DVB);framing structure，channel coding and modulation for digital terrestrial television［S］.2001.

［3］ CHOI JW，LEE Y H.Complexity－reduced channel estimation in spatially correlated MIMO－OFDM systems［J］.IEICE Trans.Communicaitons，2007，E90－B(9):2609－2612.

［4］ BARHUMI I，LEUSG，MOONEN M.Optimal training design for MIMO OFDM systems inmobilewireless channels［J］.IEEE Trans.Signal Processing，2003，51(6):1615－1624.

［5］ SANZI F，SPEIDEL J.An adaptive two－dimensional channel estimator forwireless OFDM with application tomobile DVB－T［J］.IEEE Trans.Broadcasting，2000，46(2):128－133.