基于排序QR分解的VBLAST解码算法研究

吴 军，吴云龙，黄雅兰

(江西理工大学信息工程学院，江西赣州341000)

MIMO(Multiple Input Multiple Output)技术是新一代移动通信的关键技术之一［1］，它能够提高系统容量并实现高速率的传输。1996年贝尔实验室提出的垂直分层空时码(Vertical Bell Laboratories Layered Space Time，VBLAST)［2］就有效地使用了MIMO多天线系统，它在不增加系统带宽的情况下能够成倍地提高通信系统的信息容量。作为第一个MIMO实验系统，VBLAST系统以其简单的结构和较高的频谱效率成为研究热点。对于VBLAST系统，主要的研究集中在如何设计有效的检测接收算法使检测算法的复杂度和误码性能之间得到合适的折中，其中最大似然(Maximum Likelihood，ML)检测算法［3］是最优的，但其算法的复杂度随着发射天线数和调制阶数的增加而呈指数形式增加，无法实用化。迫零(Zero Forcing，ZF)准则和最小均方误差(Minimum Mean Square Error，MMSE)准则［4］的线性检测算法性能较差，不能满足实际需要。基于上述两种准则下的串行干扰消除(Optimizing Serial Interference Cancellation，OSIC)算法虽然获得较好的性能，但每一层检测都要求信道矩阵的伪逆和对伪逆矩阵的行范数进行排序，在发射天线数较多的情况下，算法复杂度会随天线数的增加而增大［5］。QR分解可以避免信道矩阵求伪逆运算，但其检测性能不够理想［6］，所以后来提出了排序的 QR 分解(SQRD)［7］。本文在基于信号功率排序的基础上，将串行干扰消除思想和最后层分集增益应用到SQRD算法中，提出一种改进的SQRD算法。该改进的算法在性能上取得很大改善，而算法复杂度相对较低，具有很高的实用性。

1 系统模型

如图1所示，输入数据经过串并转换后变成nT层并行数据，每层数据经调制送到发射天线进行发射;发射信号经过信道到达nR接收天线，每根接收天线同时接收到带有噪声的所有发送符号，并送入VBALST译码器进行检测和判决。

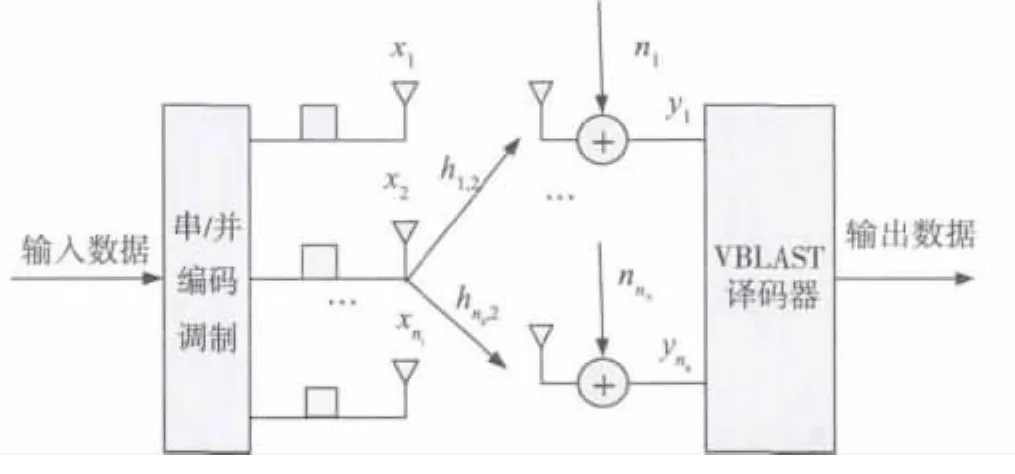
图1 VBLAST系统模型

在接收端，一根接收天线会收到每根发送天线送出的信号，将所有接收天线收到的符号作为一个矢量y=(y1，y2，…，)T来表示，将会得到

式中:x=(x1，x2，…，)T是发射信号矢量;H 是nR×nT维的信道矩阵，元素hj，i为第i(i=1，2，…，nT)根发射天线到第j(j=1，2，…，nR)根接收天线的信道增益;n=(n1，n2，…，)T是各分量独立且都服从N(0，σ2)分布的复高斯白噪声。

2 信号检测算法

2.1 QR 分解算法

该算法是将信道矩阵进行QR分解，即H=QR。其中Q为nR×nT酉矩阵，R为nT×nT上三角矩阵。用Q的共轭转置矩阵QH左乘接收信号矢量y得到

因为Q为酉矩阵，所以噪声w=QH·n统计特性不变。将式(2)展开为

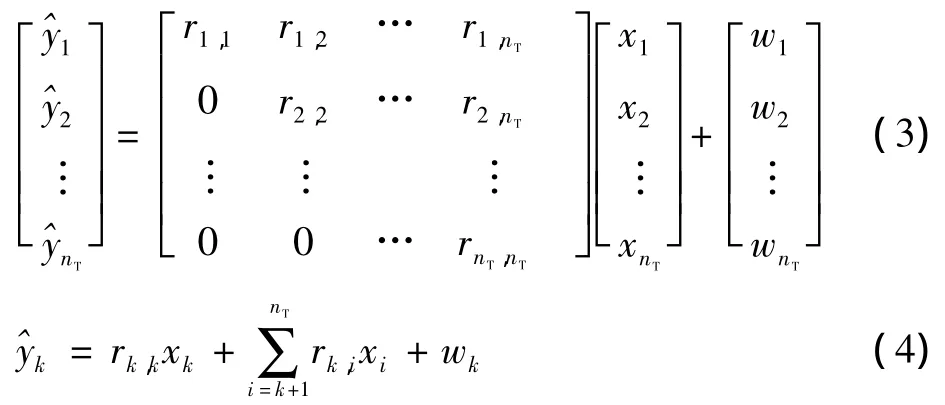
由于没有受到其他信号的干扰，因而可以先检测第nT层信号，得到估计值

式中:Q［·］是代表硬判决，硬判决就是对Demodulator输出信号做N比特量化，如果分量高于门限就认为Demodulator输出为1，否则输出为0。

2.2 改进的QR分解算法

通过信道矩阵H的QR分解，能够把发送信号矢量检测出来。从式(7)可以看出QR分解算法的检测性能取决于最先检测层，如果最先检测层出现错误，则会导致后面检测层判决符号的持续错误，这种错误传递现象称为误码传播［8］，所以提高最先检测层的准确度可以提升整个算法的误码性能。上三角矩阵R的对角线元素与对应层信号的检测后信噪比成正比，与信号估计误差成反比。所以最大的具有检测后最大的信号功率和最小的估计误差。如果得到最大的就可以提高整个算法的性能，所以对QR进行改进。

设信道矩阵 H=(h1，h2，…，hnT)，hi为 H 的列向量，将H的列向量循环左移得到

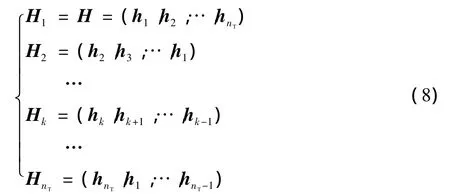
对 H1，H2，…，分别进行QR分解得到，，…，然后比较(i=1，2，…，nT)最大，对应的信道矩阵Hi=(hi，hi+1，…，hi－1)(当i=1 时，i－1=nT;当i=nT时，i+1=1)。

对Hi作上面所述的QR分解得到发射符号的估计值。

2.3 SQRD 算法

改进的QR分解算法保证了最先检测层的信号功率最大，这样在一定程度上减少了误码传播，但不能保证后续检测层是按信号功率从大到小的顺序检测，这样还是有很大的误码传播。最优的检测顺序应该是在每一步检测中都要检测具有最小估计误差的信号，因此满足最优检测顺序的R矩阵需要在检测过程的每一步最大化。为了得到最优的检测顺序，一种直接的方法就是在信道矩阵H的列向量所有全排列构成的矩阵中找到满足最优检的大小。假设测顺序的R矩阵，这样需要对信道矩阵H进行O(/2)次QR分解，计算复杂度较高。启发式的排序QR分解检测(SQRD)不能保证得到检测顺序是最优的，但以小的性能损失为代价换来复杂度的大大降低。

SQRD算法步骤如下:

1)首先按照上面改进的QR分解算法对信道矩阵H列向量进行循环左移，然后对每一个信道矩阵Hk(k=1，2，…，nT)进行QR分解，得到最大的(i=1，2，…，nT)对应的Hi。

2)对 Hi进行 QR分解，对应的检测结果为xi，xi+1，…，xi－1，通过式(6)得到最先检测层xi－1的估计。

5)重复上述步骤，直到所有信号被检测出来。

2.4 改进的SQRD算法

上述SQRD算法能保证每层检测时对应信道矩阵QR分解后得到的最大，这样很大程度上避免了误码传播现象。文献［9］表明，nR×nT信道矩阵H进行QR分解检测算法，最先检测层的分集增益是nR－nT+1，最后检测层的分集增益是nR。当发送天线数nT和接收天线数nR相等时，则最先检测层就没有分集增益。为了得到最大的分集增益，对SQRD算法进行改进，改进的SQRD算法在每次排序检测中只保留最后检测层作为估计检测层，即

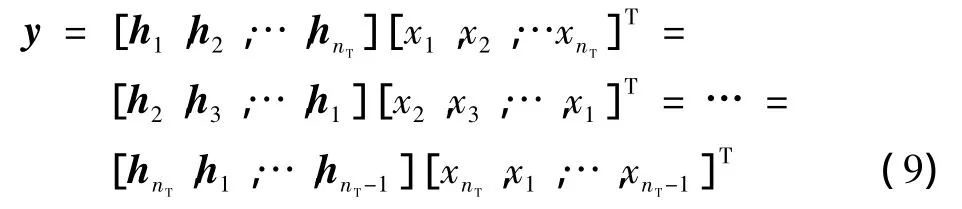
对式(9)中信道矩阵 H= ［h1，h2，…，hnT］循环移位对应的各种情况都进行QR分解，比较每种情况下所得的，找出其值最大的一种情况，设Hi=［hi，hi+1，…，hi－1］时分解所得的最大，则此时对应的发射信号为x= ［xi，xi+1，…，xi－1］T，取最后一个检测层信号xi的估计值^xi作为本次检测的最终结果。新的待检测的接收信号y'=y－xiH(:，i)，相应的信道矩阵H缩减第i列，发射天线信号矢量x缩减第i行，重复上述全部过程，直到完整的发送信号被检测出来为止。

3 仿真结果与分析

3.1 算法仿真

对文中所提出的4种检测算法进行仿真，仿真参数如表1所示。

表1 仿真参数的设置

其中信源含有10 000个符号，分成2 500帧，每帧含有4个符号。信道矩阵系数在一帧内保持不变，其实部、虚部分别为独立同分布零均值复高斯随机变量，方差为1/2。信噪比的变化范围为［0，20］dB，每个信噪比的统计平均数为100，所求误码率为100次误码数的统计平均值除以发射信源数目。仿真实验结果如图2～图4所示。

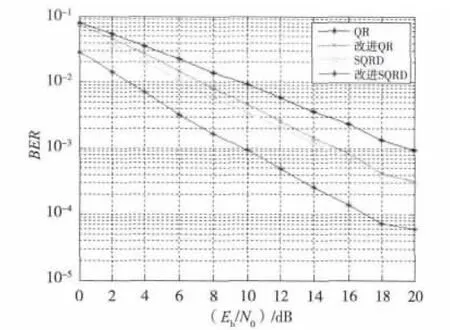
图2 4×4平坦瑞利衰落信道各检测算法性能曲线

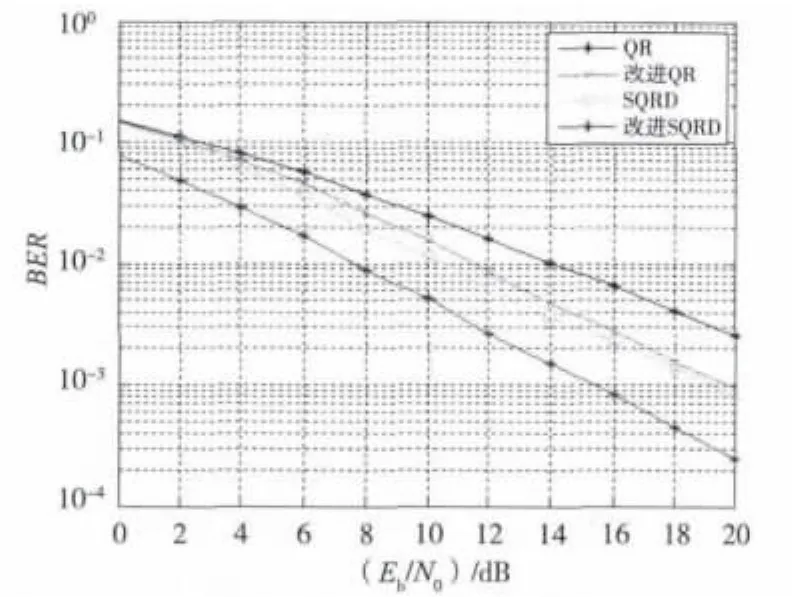
图3 4×4空间相关信道各检测算法性能曲线

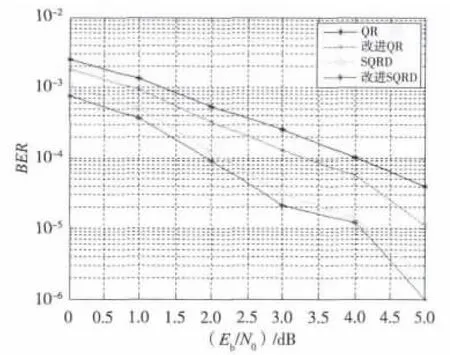
图4 4×8平坦瑞利衰落信道各检测算法性能曲线

3.2 仿真结果分析

各算法复杂度比较如表2所示。

表2 算法复杂度的比较

由图2和图3可见，在4发4收情况下，不论是平坦瑞利衰落信道和空间相关信道，两种改进算法都比原来算法的检测性能好很多。从图2中看出，改进的SQRD算法性能要优于SQRD算法4 dB左右，特别是在信噪比大于10 dB以后，基本上保持5 dB以上，这得益于改进的SQRD算法在误码传播得到有效的遏制下又得到了最后一层最大分集增益。表2可知，相应的算法复杂度上增加了检测总层数。SQRD算法性能优于改进QR算法0.5 dB到1 dB，因为检测层经过排序后遏制了误码传播现象。

由图4可知，当接收天线大于发射天线数时，系统检测性能得到明显提高。对比图2，在仿真条件均相同的情况下，4发8收系统与4发4收系统相比在误码率为10－4处，检测性能要改善至少10 dB以上。在接收端信噪比为5 dB时，即使采用检测性能最差的QR分解算法，误码率也能达到10－4数量级以上，而改进SQRD算法达到10－6数量级。这是由于接收天线数越多，系统的接收分集越大，使衰落的可能性减少，误码率明显降低。

4 结论

本文对MIMO技术中广泛应用的VBLAST系统接收端检测算法进行了研究，在传统的QR分解算法中存在两个主要问题:误码传播现象和最先检测层获得的分集增益最小。针对以上问题提出了一种改进的SQRD算法，它不但能有效遏制误码传播现象，而且能够取得最后检测层的最大分集增益，从而带来性能上的改善，特别在接收天线较多的情况下，检测性能得到明显提高。本算法的复杂度比SQRD的复杂度略有增加，不过其检测性能较好，而且可以有效地避免传统算法中复杂的信道矩阵求伪逆运算。改进的SQRD算法在相对不高的复杂度下拥有优秀的系统检测性能，符合新一代无线通信的要求，具有较高的实用性。

［1］张建忠，李宏伟，邓东虎.一种低复杂度的空时分组码检测算法［J］.电视技术，2011，35(2):67－68.

［2］ BROWNE DW，MANTEGHIM，FITZM P，et al.Experiments with compact antenna arrays for MIMO radio communications［J］.IEEE Trans.Antennas and Propagation，2006，54(11):3239－3250.

［3］ SHAKO SH，TANG Y X，KONG T，et al.Performance analysis of a modified V－BLAST system with delay offsets using zero－forcing detection［J］.IEEE Trans.Vehicular Technology，2007，56(2):3827－3837.

［4］ PAULRAJA，NABAR R，GORE D.Introduction to space－time wireless communications［M］.［S.l.］:Cambridge University Press，2003:1－270.

［5］ HASSIBI B .An efficient square－root algorithm for blast［C］//Proc.IEEE International Conference on Acoustic，Speech，Signal Processing.Istanbul，Turkey:IEEE Press，2000:5－9.

［6］ UBBEN DW，RINAS JM，OHNKE R B，et al.Efficient algorithm for detecting layered space－time codes［C］//Proc.International ITGConference on Source and Channel Coding.Berlin，Germany:IEEE Press，2002:399－405.

［7］史开新.MIMO系统中信号检测技术的研究［D］.西安:西安电子科技大学，2008.

［8］李永杰，傅洪亮.一种改进的QR分解VBLAST解码算法［J］.系统仿真学报，2010，22(6):1447－1449.

［9］ LIU Haitao，CHEN Xingqing，LIDaoben，et al.A joint M－IQRD and ML detection algorithm for V－BLAST［C］//Proc.GMC.Beijing:Electronic Industry Press，2005:18－22.