自升式平台桩靴承载力研究
庞雪涛,冯国庆,任慧龙
(哈尔滨工程大学,哈尔滨150001)
0 引言
自升式平台是海上油气勘探、开发的主要设备之一[1,3],但我国沿海地层复杂,部分地质疏松,且自升式平台是唯一使用桩靴来承受海底对平台作用力的海洋平台,鉴于这一特性,在安装或作业的时候有可能发生桩靴入泥过深导致平台倾斜失效的严重事故。实践经验表明,由于地基土的承载力不足而使平台发生危险的例子非常多,在操作时保证平台的桩靴不要入泥太深,即地基土有足够的承载力就显得尤为重要。
挪威SINTF、英国City University和美国SNAME都发表过自升式平台桩靴与土的相互作用的研究论文,研究方法多为理论分析、海上现场实测和实验室测试,挪威船级社有专门针对自升式平台的地基承载力计算的公式介绍[6]。使用地基承载力经验公式计算所得的地基承载力并不能真实的反映地基土的实际情况,且海上现场实测又较为复杂,由于较接近于土体的本构模型的出现,使用数值模拟的方法来预估地基承载力更能真实的反映地基土的实际情况,且更为容易实现。
通过使用地基承载力经验公式和数值模拟,分析比较两种方法所计算的地基承载力差别,进行土体特性参数对地基土承载力的影响规律的计算,从而对工程人员对自升式平台的安装选址和平台的安全作业提供指导性建议。
1 地基土承载力经验公式
海洋土主要为砂土和粘土,土的抗剪强度对平台基础的设计有重要影响。抗剪强度与土的内摩擦角和粘聚力有关,表1列出了粘土的粘聚力范围[7]。

表1 粘土的粘聚力范围
1.1 砂土地基土的极限承载力计算公式
地基土为砂土时,采用Peck和Terzaghi提出的公式计算:

式中:qu为地基极限承载力;B为桩靴的宽度;Nr和Nq为承载力系数,查文献[7]图形可得;D为海底泥面到桩靴计算断面的深度;γ为桩靴计算断面处土的有效容重;γ1为桩靴计算断面下B/2范围内土的平均有效容重;γ2为桩靴计算断面以上土的有效容重;V为桩靴排开土的体积;A为桩靴最大截面面积。
1.2 粘土地基土的极限承载力计算公式
当桩靴插入土壤时,地基土被挤开,此时被挤开的地基土会出现回填和非回填两种情况,对计算地基土的极限承载力影响很大。通常情况下,以Skempton公式计算[2]。
(1)有回填情况极限承载力
地基土的极限承载力计算公式为:

式中:NC为承载力系数,查文献[7]图形可得;su为桩靴计算断面下B/2范围内土的平均不排水抗剪强度。
skempton给出承载力系数NC的计算方法[7]:

式中:L为桩靴的长度。
当满足su相当于一个常数和D/B<2.5两个条件时,公式(2)适用。若桩靴计算断面下2B/3范围内土的抗剪强度变化达±50%时,此式不再适用。
(2)非回填情况
地基土的极限承载力计算公式为:

2 自升式平台桩靴入土的数值模拟方法
有限元数值模拟方法能够比较真实的反映桩靴与地基土之间的相互作用关系,因而在分析地基承载力时应用广泛。
2.1 地基土的弹塑性基本理论
土是弹塑性介质,其本构模型主要建立在塑性增量理论基础上。地基土的本构关系由以下三个方面组成:
(1)屈服准则与破坏准则,确定材料塑性变形开始时和破坏前的极限应力状态。当材料的单向屈服值超过屈服准则定义的极限时,材料出现塑性应变。材料发生塑性应变时需要满足屈服函数:

式中:C是常数;f(σ)取决于地基土应力状态。对于各相同性材料,屈服与坐标无关,因此:

用应力张量不变量表示为:


(2)流动准则,确定应变的方向。当材料受单向作用力时,应变方向与应力方向一致,三维受力时,有6个应变分量。流动准则假定,塑性势Q的应力梯度与塑性应变增量成正比:

式中:Q为塑性乘数;dλ是一个大于0的比例因子。
(3)硬化准则,确定在材料硬化后仍然发生塑性变形时应力状态应满足的规律。这里将地基土的模型认为是理想的,不考虑硬化准则。
2.2 ABAQUS中的Mohr-Coulomb模型理论
Mohr-Coulomb塑性模型主要适用于单调荷载下的颗粒状材料,在岩土工程中应用非常广泛。其基本理论主要包括屈服面和塑性势面两方面。
(1)屈服面,模型屈服面函数为:

式中:φ是q-p应力面上Mohr-Coulomb屈服面的倾斜角,称为材料的摩擦角;c是材料的粘聚力;Rmc控制了屈服面在π平面的形状。
(2)塑性势面,为了避免在尖角处出现塑性流动方向不唯一,导致数值计算繁琐,收敛缓慢的问题,ABAQUS采用了连续光滑的椭圆函数作为塑性势面:

式中:Ψ是剪胀角;c0是没有塑性变形时的粘聚力;ε是子午面上的偏心率,控制了G在子午面上的形状与函数渐近线之间的相似度;Rmw控制了G在π面上的形状。
Mohr-Coulomb模型使用时应注意以下事项:(1)只适用于ABAQUS/Standard;(2)需和线弹性模型联合使用;(3)必须采用非对称求解器,尤其是对应极限承载力计算的情况,否则可能出现数值不易收敛的问题。
2.3 桩靴入土数值模拟要点
模型的创建与网格划分:首先采用MSC/Patran完成土壤和桩靴的几何建模和有限元网格划分。由于自升式平台具有大桩靴,入泥深度较浅,鉴于这一特点,在对土体进行网格划分时,在桩靴贯入土体的范围内将土体分为较小的网格,逐渐向四周增大,将生成的模型导入ABAQUS中。
土体范围的选取与边界条件的约束:根据实际情况,土体范围为无限大,在进行数值模拟的过程中,取有限边界的土体来模拟无限边界。若土体边界过大,则造成计算费时繁琐,若土体边界较小,则不可避免的对计算结果带来误差,根据Hossain等人的观点,文中取土体的深度和直径均为50m。根据实际情况,对土体侧面约束水平位移,顶面自由,底面用多点约束关联到一点上,并施加固定约束。
桩靴入土数值模拟的基本假定:(1)桩靴材料为钢材,其所受的力主要为轴向力,简化为平面问题;(2)土体为粘性土,采用Mohr-Coulomb模型;(3)桩靴与土一旦接触就不再分离,摩擦类型为库伦摩擦。
荷载的施加与桩靴贯入阻力数据的提取:在计算实例中,固定桩靴贯入的位移,在桩靴达到贯入位移的过程中,ABABQUS自动计算贯入每个位移处时所需要的力,此力即为桩靴贯入的阻力。通过对桩靴贯入阻力的分析可以预估地基土的承载力。
3 实例分析计算
3.1 有限元模型和参数
桩靴的有限元模型如图1所示,参数见表2;土体的有限元模型如图2所示,参数见表3。

图1 桩靴的有限元模型

图2 桩靴和土壤的有限元模型

表2 桩靴的参数

表3 土的参数
3.2 理论计算与数值模拟对比
将桩靴的底面中心设置为提取应力的参考节点,以桩靴受到的垂直作用力(地基承载力)为纵坐标,桩靴贯入深度为横坐标,当桩靴最大贯入深度为5m时,理论计算与数值模拟的计算结果如图3所示。
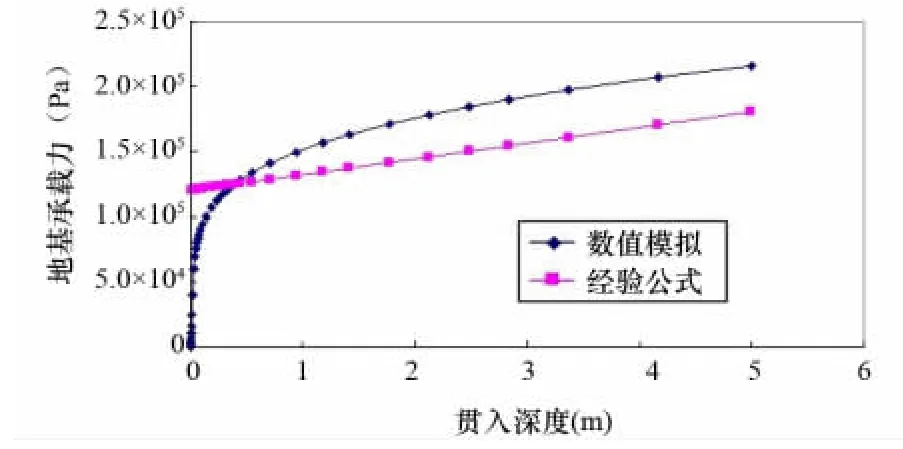
图3 理论计算与数值模拟的对比
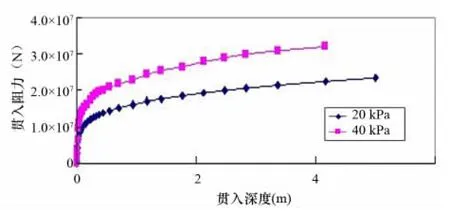
图4 贯入阻力—入泥深度关系
由图3可知,根据理论公式(2)和(4)计算所得到的地基承载力与贯入深度之间呈线性关系,而数值模拟曲线在开始阶段为直线,当地基承载力达到某一极限值时,桩靴的贯入深度急剧增加,此时地基土发生破坏,即出现桩靴的“穿刺”现象。从图3中可以看出,当桩靴所受的垂直作用力超过140kPa时,其贯入深度急剧增加,因此可以预测该处的地基承载力约为140kPa,此时贯入深度约为70cm,与理论计算得到的结果误差约为7.4%。
3.3 贯入深度对贯入阻力的影响
分别选取粘聚力c=40kPa和c=20kPa两种工况计算,其余参数见表2和表3,计算结果如图4所示。图中曲线的变化趋势相同,但在同一深度处,土的粘聚力越大(抗剪强度越高),贯入阻力越大(地基承载力越大)。
3.4 土的参数对地基承载力的影响
(1)弹性模量的影响
分别选取土的弹性模量为100、80、60、40、20、8进行计算,其余参数参见表2和表3,计算结果如图5所示。由曲线可知,在贯入深度相同时,桩靴贯入阻力(地基承载力)随土体弹性模量增大呈增长趋势。
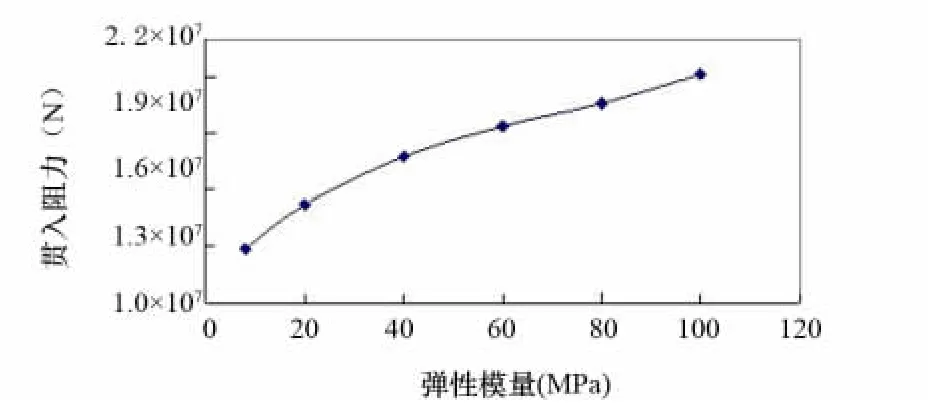
图5 弹性模量的影响

图6 粘聚力的影响
(2)粘聚力的影响
分别选取土的粘聚力为80、60、40、20、10进行计算,其余参数参见表2和表3,计算结果如图6所示。由曲线可知,在贯入深度相同时,随着粘聚力增大,桩靴贯入阻力(地基承载力)几乎成线性增长。
(3)内摩擦角的影响
分别选取土的内摩擦角为10°、7.5°、5°、2.5°、0°进行计算,其余参数参见表2和表3,计算结果如图6所示。由曲线可知,在贯入深度相同时,随着内摩擦角的增大,桩靴贯入阻力(地基承载力)几乎呈线性增长。

图7 内摩擦角的影响
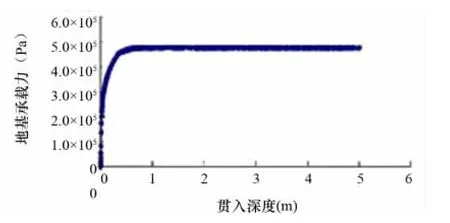
图8 地基承载力计算
3.5 极限承载力的校核
选取某一具有相同桩靴的三桩靴海洋平台进行地基土的极限承载力校核。通过提取桩靴所受的垂直力与计算所得的地基承载力比较,以判断该条件下的地基土是否能够承受该海洋平台。三桩靴所受的垂直力分别为29 030 344N,36 808 560N,36 807 180N,选取桩靴所承受的最大力进行比较。由图3可知,在土体粘聚力c=20kPa,内摩擦角φ=0,弹性模量E=20MPa时,地基土的承载力约为15 120kN,显然小于36 809kN,此时地基土不能承受该海洋平台,需要选取更硬的地基土。设置土体参数粘聚力c=80kPa,内摩擦角φ=5°弹性模量E=100MPa,其余参数同前,数值计算得到的地基承载力如图8所示。
由图8得知,当桩靴贯入深度约为50cm时,地基土的极限承载力约为480kPa,垂直力约为52 000 kN,大于36 809kN,此条件下的地基土能够承受该海洋平台。
4 结语
(1)对于桩靴入土,理论计算与有限元数值模拟结果接近,但理论计算被认为较实际情况偏于保守,在新的更接近于地基土的本构模型出现以前,理论计算与数值模拟仍是研究桩靴入土的重要手段。
(2)在贯入深度一定时,桩靴的贯入阻力随地基土的弹性模量、粘聚力和内摩擦角的增大而增大。
(3)对于其他未进行计算的情况可参考该方法进行计算,对工程人员选取地基土有一定的指导意义。
[1]付军强.海上可移动钻井装置发展综述与展望[J].中国海洋平台,2003,18(5):6-9.
[2]郑喜耀.自升式钻井平台插桩深度计算及几个问题的探讨[J].中国海上石油(工程),2000,12(2):18-21.
[3]Paul Dempsey.Liftboats go international with ten-fold jump in business[J].Offshore,2002.
[4]艾金发.有限元方法在岩土工程中的应用[J].科技风,2009,3(4):78-79.
[5]李强.基于桩土相互作用的自升式平台桩靴强度研究[D].大连:大连理工大学,2008.
[6]付丽娜.自升式钻井船桩靴承载能力研究[D].天津:天津大学,2008.
[7]陈希哲.土力学地基基础[M].北京:清华大学出版社,1998.
[8]朱以文,蔡元奇,徐晗.ABAQUS与岩土工程分析[M].北京:中国图书出版社,2005.

