基于转矩补偿的风电变桨加载系统的研究及仿真

余清清，孙 勇，周 浩

(浙江运达风电股份有限公司 风力发电系统国家重点实验室，浙江 杭州 310012)

0 引言

变速变桨距风力发电机组目前已成为大型风力发电机组研发和应用的主流机型，风力发电系统中的电动变桨技术不但改善了桨叶和整机的受力状况，而且优化了风力发电控制系统，使整机获得了最优发电效率［1-3］。

变桨控制系统根据风速变化实时调节桨距角。在低风速起动时，桨叶调整到合适角度，使风轮获得最优起动力矩;当风速过高时，系统通过调整桨叶，改变气流对叶片的攻角，从而改变风力发电机组获得的空气动力转矩，使机组功率输出保持稳定。

我国的风力发电技术起步晚，风力发电变桨系统方面的测试就更晚了。近些年国内涌现出不少变桨系统测试台，但国内的测试台无论从模型建立还是控制方法上均存在很多不足，变桨系统的测试方法也处在较低水平。变桨系统的性能对于风电机组的稳定运行起到关键的作用，笔者对如何建立能够真实模拟风电机组变桨系统运行工况的加载试验系统进行了研究。

风力发电系统国家重点实验室成功建设变桨系统试验台。研究通过Bladed 风电机组仿真软件与机组主控控制变桨系统的输出，同时Bladed 仿真软件模拟各种风况，试验台根据不同风况给出相应的载荷。电机加载采用转矩闭环控制［4］方法，确定桨叶模拟系统的补偿转矩［5-7］，使得控制准确性高、反应速度快，试验台可模拟任何机型的桨叶在不同工况下运行并进行测试。

1 变桨系统试验台介绍

试验台由两个系统组成:加载系统和变桨系统。加载系统主要有风机仿真软件、控制系统和数据采集装置、变频器、加载电机、扭矩仪、编码器等。变桨系统主要由风机主控、变桨控制器、变桨驱动器、变桨电机等组成。风电机组变桨加载试验台的结构框架如图1所示。

图1 风电机组变桨加载试验台的结构框图

试验台实物图如图2 所示。

图2 风电机组变桨加载试验台的实物图

Bladed 仿真软件配合机组主控建立不同工况的模型，通过计算得出相应数据，将模拟的机组数据发送给风电机组主控，并通过变桨控制柜与变桨驱动器，实现对变桨电机的控制，将模拟的电机加载转矩值发送给试验台数据采集系统处理，试验台控制系统对收到的目标转矩值进行转矩补偿处理，并将处理后的目标转矩值发送至加载系统中的变频器，控制变频器根据目标转矩对电机进行转矩补偿。

该设计采用的转矩闭环控制方法，对加载电机进行转矩补偿，可采用分段补偿的方法，根据任何一段时间内的起始和终止时间风速对应的转矩差值来得出这段时间内的转矩变化量。

转矩闭环控制方法可以利用高采样率、高精度的扭矩传感器每隔一段时间采集和测量加载电机的输出转矩并发送给控制中心，对加载系统进行分段补偿，高采样率、高精度的扭矩传感器能够可靠地完成转矩的采集工作，采集率可以达到6 kHz。

2 桨叶模拟系统的补偿转矩分析

2.1 模拟桨叶的输出转矩变化量

本研究将Bladed 仿真软件中空气动力学产生的转矩和摩擦力产生的转矩，进行叠加计算后确定为所模拟桨叶的输出转矩。将不同风速下得到的所模拟桨叶的输出转矩做差值运算，得到所模拟桨叶的输出转矩变化量。

下面将通过推导公式对上述步骤予以阐述:

公式如下:

式中:ΔT1—所模拟桨叶的输出转矩变化量;TM—风速为v1时，对应的所模拟桨叶的输出转矩值;T0—风速为v0时，对应的所模拟桨叶的输出转矩值。

该转矩闭环控制方法用于对加载电机进行转矩补偿，研究者可采用分段补偿的方法，根据任何一段时间内，起始和终止时间风速对应的转矩差值来得出这段时间内的转矩变化量。

2.2 加载系统的补偿转矩

(1)确定被模拟桨叶的总转动惯量与模拟桨叶输出转矩的加载系统的总转动惯量的差值;

(2)将差值与被模拟桨叶的总转动惯量做除法运算;

(3)确定除法运算的结果与所模拟桨叶的输出转矩变化量的乘积，得到加载系统的补偿转矩。

下面将通过推导公式对上述步骤予以阐述:

由所模拟桨叶的运动方程:

加载系统的运动方程:

由于试验平台变桨加载系统是用加载电机来模拟桨叶，通过计算后得出J1与J2不相同，经过相同的转矩变化量ΔT1后，两者的转速变化是不相同的。

本研究将现有技术中的目标转矩经过转动惯量补偿算法计算后，作为目标转矩中的补偿转矩，就可以真实地模拟桨叶的动态特性。

得到施加转动惯量补偿后的加载系统的动态特性:

这样，加载电机与桨叶经过两种相同的转矩变化的同时，加载电机经过齿轮箱速比折算后，会经历相同的转速变化，相当于对加载系统施加了额外的转矩，可以达到转矩补偿的目的。

则:

由式(2，5)推导，得出:

式中:J1—被模拟桨叶的总转动惯量，dω1/dt—模拟桨叶的转速变化率，J2—模拟桨叶输出转矩的加载系统的总转动惯量，dω2/dt—加载系统的转速变化率，ΔT1—模拟桨叶的输出转矩变化量，ΔJ—加载系统的补偿转动惯量，ΔT—加载系统的补偿转矩。

2.3 补偿转矩的折算

对于该加载系统，并未模拟变桨系统中的速比变化，故在模拟桨叶的加载系统的补偿转矩必须进行速比折算，生成加载电机的补偿转矩。本研究将转速比与加载系统的补偿转矩进行乘法运算。

下面将通过推导公式对上述步骤予以阐述:根据式(6)得到:

式中:λ—变桨系统中的低速轴与高速轴的转速比，ΔTH—加载系统中的加载电机的补偿转矩。

本研究在对加载系统的补偿转矩进行折算后，生成加载电机的补偿转矩，结合测得的加载电机的实际输出转矩，生成加载电机的目标转矩，并将目标转矩向加载系统中的变频器发送，控制变频器根据目标转矩对加载电机进行转矩补偿。

3 仿真结果与试验结果的分析

本研究依据上述的转矩补偿理论，基于2.5 MW风电机组Bladed 模型［8-9］和加载系统，搭建了试验平台，在该平台上模拟了风电机组运行工况下的变桨转矩并通过加载系统给变桨系统加载，风电机组工况仿真结果:风速曲线如图3 所示。发电机转速曲线如图4 所示。桨距角曲线如图5 所示。功率曲线如图6所示。

图3 风速曲线

图4 发电机转速曲线

图5 桨距角曲线

图6 功率曲线

本研究利用Bladed 仿真软件运行上述工况，将Bladed 中的空气动力学产生的转矩和摩擦力［10］产生的转矩，进行叠加计算及转矩补偿计算后仿真得出加载电机的响应波形，仿真结果如图7 所示。

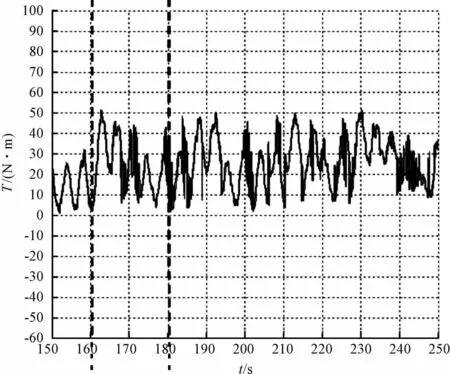
图7 仿真的加载电机的响应曲线

本研究采用与上述一样的机组模拟相同的工况，将Bladed 软件中模拟的机组工况通过风机主控实时传给变桨系统来控制变桨电机转速;将Bladed 模拟的桨叶输出转矩值通过风机主控以模拟量信号实时传给加载系统，经过转矩补偿处理后对加载电机进行转矩闭环控制，测试结果如图8 所示。

图8 实测加载电机响应曲线

(1)从图7 中160 s～180 s 的曲线和图8 的响应曲线比较可知，相同的仿真工况下，仿真形成的响应曲线和实测的响应曲线基本上一致;

(2)由图8 可知，加载电机转矩给定值与实测值基本一致，跟随性也基本保持同步，验证了利用转矩闭环控制能达到对加载电机的良好控制;

(3)从仿真结果和试验数据两方面验证了转矩补偿处理优化了变桨加载试验台。

4 结束语

本研究介绍了利用Bladed 仿真软件，通过转矩闭环控制与转矩补偿优化相结合的控制方法，实现了变桨系统的半物理，为变桨系统的测试与开发提供了可靠的平台。研究中分析了桨叶模拟系统的转矩补偿，推导出了加载系统补偿转矩的公式，最后经过速比折算，得出系统中加载电机的补偿转矩值。

基于2.5 MW 风电机组Bladed 模型进行仿真及加载试验，通过软件仿真与试验台实测对比，仿真结果与实测数据基本保持一致，验证了转矩补偿能优化加载控制。研究中介绍的转矩补偿可应用到不同工程上，为优化控制提供参考。

［1］叶杭冶.风力发电机组监测与控制［M］.北京:机械工业出版社，2011.

［2］宋海辉.风力发电技术及工程［M］.北京:中国水利水电出版社，2009.

［3］叶杭冶.风力发电机组的控制技术［M］.2 版.北京:机械工业出版社，2006.

［4］冯国楠.现代伺服系统的分析与设计［M］.北京:机械工业出版社，1990.

［5］盛朝强，谢昭莉.基于电惯量的汽车惯性式制动试验系统的设计［J］.重庆大学学报:自然科学版，2005，28(1):90-92，101.

［6］朱晓锦，张为公，金伟民，等.汽车同步器试验系统机械惯量电模拟研究与实现［J］.汽车工程，2001，23(2):134-138.

［7］张安明，柴建云，王善铭，等.电力系统动态模拟中发电机组转动惯量的补偿［J］.清华大学学报:自然科学版，2006，46(10):1661-1664.

［8］SORENSEN J D，SORENSEN J N.Wind energy systems:optimising design and construction for safe and reliable operation［M］.Cambridge:Woodhead Publishing Limited，2011.

［9］BIANCHI F D，BATTISTA H D，MANTZ R J.Wind turbine control systems principles modelling and gain scheduling design［M］.北京:机械工业出版社，2009.

［10］贺德馨.风工程与工业空气动力学［M］.北京:国防工业出版社，2006.