存在信道反馈延迟时Turbo-BLAST系统的自适应功率分配算法

于晓丹 陈小敏谭 伟 虞湘宾

(南京航空航天大学电子信息工程学院 南京 210016)

1 引言

在 Turbo-BLAST系统中采用链路自适应技术可以有效改善系统性能[1,2]。其中，发送功率分配是一种简单可行的方法，根据不同的优化目标，可选用不同的发送功率分配方案。以信道容量为优化目标的注水功率分配算法可显著提高系统容量[35]-，而以系统误比特率(Bit Error Rate, BER)为优化目标的自适应功率分配算法可以有效改善系统的BER性能[68]-。

近年来，自适应功率分配算法得到广泛应用[9,10]，以最小化系统BER为优化目标，文献[6,7]分别提出一种基于迫零(Zero Forcing, ZF)和最小均方误差(Minimum Mean Square Error, MMSE)检测的自适应功率分配算法；文献[8]给出了一种基于MMSE软干扰抵消迭代检测的发送功率分配方案，较大程度改善了系统的BER性能。功率分配的性能取决于信道状态信息(Channel State Information, CSI)，而在实际应用中信道信息的反馈存在时延或误差[11]。已有文献针对反馈时延对系统性能的影响做了研究[12,13]，但没有给出反馈时延对功率分配性能的影响。

为提高功率分配算法的工程应用价值，本文针对存在信道反馈延迟的Turbo-BLAST系统，推导出系统BER的表达式，在总功率约束条件下，以BER为优化目标，提出基于拉格朗日极值法的次优功率分配方案和基于牛顿迭代法的最优功率分配方案。仿真结果表明，本文推导的BER表达式可以有效评估反馈时延对系统性能的影响，提出的两种自适应功率分配算法均可改善系统的BER性能。

2 存在信道反馈延迟的Turbo-BLAST系统模型

Turbo-BLAST系统有M根发送天线和N根接收天线，比特流经过编码、调制、空时变换和功率加载后发送出去，信道为准静态瑞利衰落，某一时刻接收信号可表示为

图1 信道反馈有延迟时的系统模型

3 信道反馈有延迟条件下Turbo-BLAST系统的BER推导

接收端采用基于 ZF准则的软干扰抵消算法进行检测，检测用的权向量矩阵为，则发送信号的估计为

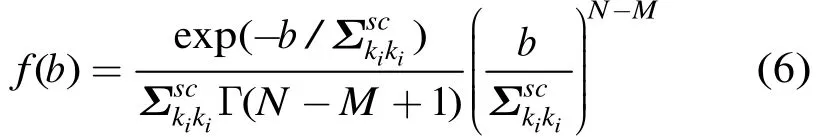
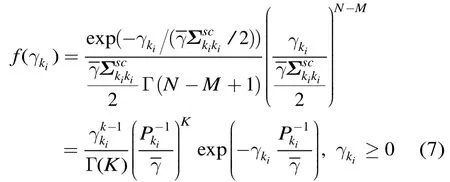
已知采用 M-QAM 调制时第ik个发送符号的BER表达式[6]，则t时刻的系统瞬时BER可表示为

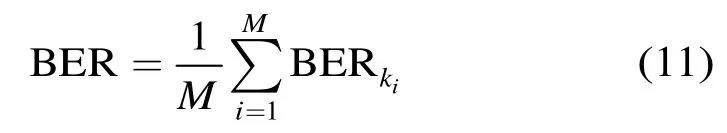
本节推导出了信道反馈有延迟时系统 BER的表达式，下面将在总功率约束条件下以BER为优化目标，分别给出次优和最优的功率分配矩阵的求解过程。

4 信道反馈有延迟条件下的自适应发送功率分配方案

4.1 次优的自适应功率分配算法

在总发送功率约束条件下，以系统总BER为优化目标的约束优化问题可以描述为

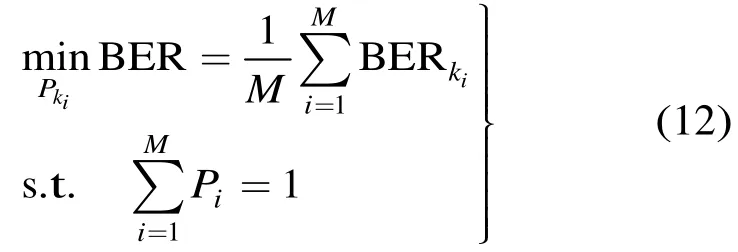
式(12)的约束优化问题可以采用拉格朗日极值法求解，则代价函数可表示为

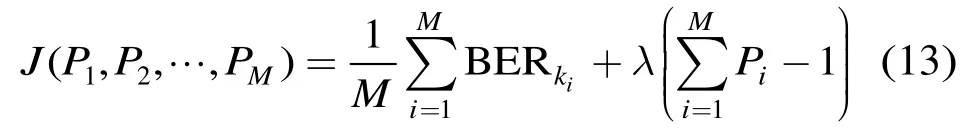
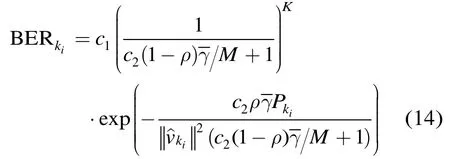
利用式(14)重新构造代价函数，便可得到次优的功率分配矩阵和拉格朗日乘子：

4.2 最优的自适应功率分配算法

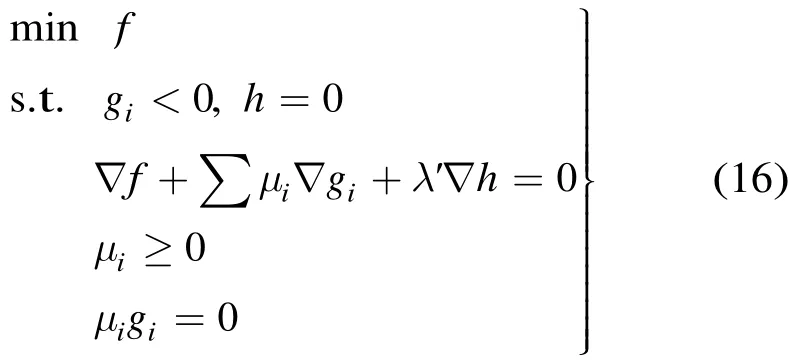
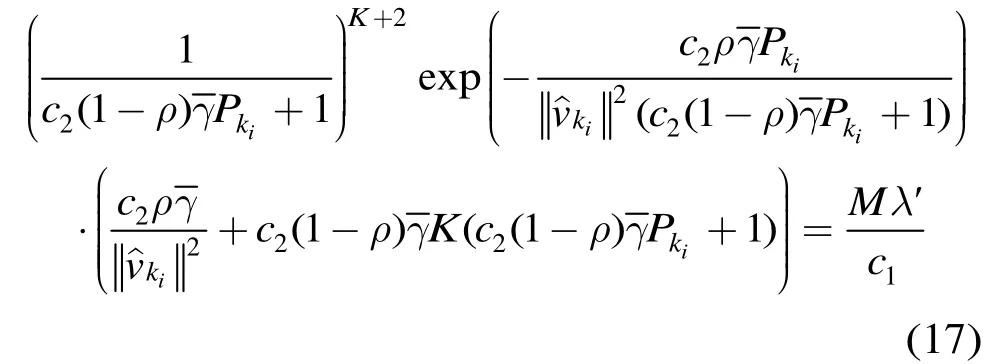
对式(17)等号两边取对数，可得代价函数：

4.3 复杂度分析

本节给出求解发送功率分配矩阵次优解与最优解的计算复杂度比较，如表1所示。

表1 求解次优解与最优解的复杂度比较

从表1可以看出，次优功率分配算法虽对BER做了近似，但其计算复杂度相比于最优功率分配算法大大降低。

5 仿真结果

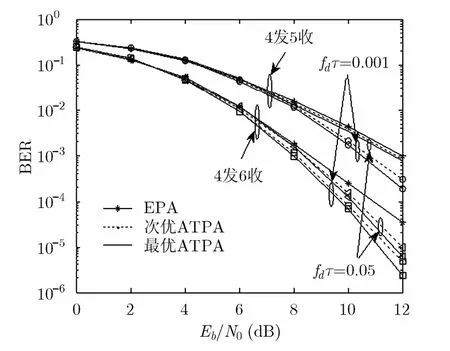
图2 迭代次数不同时次优/最优功率分配算法与等功率算法的性能比较

图3 迭代次数对最优与次优ATPA算法性能的影响

本节通过仿真实验给出系统的BER性能，以验证所提算法的有效性。在图2-图3的仿真中，信道是准静态瑞利衰落，假设接收端完全已知信道状态信息。发送端采用(2,1,2)卷积编码，4-QAM调制，接收端采用基于ZF准则的软干扰抵消检测，BCJR译码。iter表示迭代次数，表示归一化反馈时延，EPA表示等功率分配算法，最优次优ATPA表示最优次优功率分配算法。

从图2可以看出，和等功率分配相比，采用本文所提的两种功率分配算法均可明显改善系统性能，在，接收天线数为6时，采用最优功率分配算法要比采用等功率算法提高约1.2 dB，比采用次优功率分配算法提高约0.3 dB。另外，系统性能随着接收天线数目的增大，归一化反馈时延df τ的降低而逐渐变好，说明系统的接收分集越大系统性能越好，并且可以有效反映归一化反馈时延对系统BER性能的影响，与理论预期结果一致。

从图3可以看出， 接收端的迭代检测算法可进一步改善系统的BER性能，无论对次优的功率分配算法还是最优的功率分配算法，随着迭代次数的增加，系统的BER性能均得到了改善。这说明本文所提算法在信道反馈有延迟时仍然是有效的。

6 结束语

针对信道反馈有延迟的 Turbo-BLAST系统，提出次优和最优两种自适应功率分配算法，通过仿真验证了所提算法的有效性。最优功率分配方案可以显著改善系统的BER性能，次优功率算法具有较低的算法复杂度，基于 ZF的软干扰抵消迭代检测算法进一步改善了系统的BER性能。由于本文接收端采用的检测基于 ZF准则，虽可抑制信号干扰，但同时也损失了部分有用信息，因此，在以后的工作中，将进一步研究信道反馈有延迟情况下，基于MMSE检测的自适应功率分配算法。

[1] Chen Xiao-min, Yu Xiang-bin, Zhu Qiu-ming, et al.. Waterfilling power allocation scheme for Turbo-BLAST system with imperfect channel state information[C]. IEEE 4th International Symposium on Microwave, Antenna,Propagation, and EMC Technologies for Wireless Communications, Beijing, 2011: 611-614.

[2] Sellathurai M and Haykin S. Turbo-BLAST for wireless communications: theory and experiments[J]. IEEE Transactions on Signal Processing, 2002, 50(10): 2538-2546.

[3] 李晓辉, 易克初, 刘乃安. 一种MIMO系统中的新型资源分配算法[J]. 电路与系统学报, 2006, 11(5): 84-87.Li Xiao-hui, Yi Ke-chu, and Liu Nai-an. A novel resource allocation algorithm for MIMO system[J]. Journal of Circuits and Systems, 2006, 11(5): 84-87.

[4] 姜永权, 刘乃安, 沈民奋, 等. MIMO系统一种新的功率分配算法及容量分析[J]. 电子学报, 2007, 35(9): 1749-1753.Jiang Yong-quan, Liu Nai-an, Shen Min-fen, et al.. A novel power allocation algorithm for MIMO system and capacity analysis[J]. Acta Electronica Sinica, 2007, 35(9): 1749-1753.

[5] Kostina V and Loyka S. Optimal power and rate allocation for coded V-BLAST: instantaneous optimization[J]. IEEE Transactions on Communications, 2011, 59(10): 2841-2850.

[6] Nam Seung-h, Shin Oh-s, and Lee Kwang-b. Transmit power allocation for a modified V-BLAST system[J]. IEEE Transactions on Communications, 2004, 52(7): 1074-1080.

[7] 许威, 赵春明, 史志华, 等. MIMO系统中基于ZF/MMSE检测的自适应功率分配方案[J]. 电子学报, 2008, 36(10):1891-1897.Xu Wei, Zhao Chun-ming, Shi Zhi-hua, et al.. Adaptive power allocation for ZF/MMSE detected MIMO systems[J]. Acta Electronica Sinica, 2008, 36(10): 1891-1897.

[8] 唐万斌, 张亮, 李少谦. V-BLAST系统中采用发射功率分配的MMSE迭代软干扰抵消算法[J]. 电子与信息学报, 2006,28(9): 1640-1644.Tang Wan-bin, Zhang Liang, and Li Shao-qian. MMSE iterative soft interference cancellation algorithm using transmit power allocation scheme in V-BLAST system[J].Journal of Electronics ＆amp; Information Technology, 2006, 28(9):1640-1644.

[9] Karami M and Beaulieu N C. Channel adaptive power allocation and pilot optimization for OFDM systems[C].IEEE Global Communications Conference on Wireless Communications, Anaheim, CA, 2012: 4893-4899.

[10] Heo Ayoung, Cho Yeon-j, Jin Seung-r, et al.. Adaptive relay selection and power allocation for hybrid relay systems[C].International Conference on Future Generation Communication Technology, London, 2012: 117-120.

[11] Zhou S L and Giannakis G B. Optimal transmitter eighenbeamforming and space-time block coding based on channel mean feedback[J]. IEEE Transactions on Signal Processing,2002, 50(10): 2599-2613.

[12] 赵爽, 杨鸿文. 时变瑞利信道下反馈时延对选择发送分集性能的影响[J]. 北京邮电大学学报, 2009, 32(4): 94-99.Zhao Shuang and Yang Hong-wen. The impact of feedback delay on the performance of selective transmit diversity under time-varying Rayleigh channel[J]. Journal of Beijing University of Posts and Telecommunications, 2009, 32(4):94-99.

[13] Guharoy S and Mehta N B. Joint evaluation of channel feedback schemes, rate adaptation, and scheduling in OFDMA downlinks with feedback delays[J]. IEEE Transactions on Vehicular Technology, 2013, 62(4):1719-1732.

[14] Gore D A, Jr Heath R W, and Paulraj A J. Transmit selection in spatial multiplexing systems[J]. IEEE Communications Letters, 2002, 6(11): 491-494.

[15] Alouini M S and Goldsmith A J. Adaptive modulation over Nakagami fading channels[J]. Wireless Personal Communications, 2000, 13(1/2): 119-143.