基于串联信号延迟对消法的三相非理想电网锁相控制策略

吴 恒 杨东升 阮新波

（南京航空航天大学自动化学院航空电源重点实验室 南京 210016）

1 引言

由于能源危机和环境污染，可再生能源的利用越来越得到人们的重视，而并网逆变器作为可再生能源发电与电网的接口，起着将可再生能源发出的电能转变为交流形式向电网输送的重要作用，因此并网逆变器安全稳定运行对可再生能源的利用具有重要意义。

逆变器在并网运行时，其输出电压被电网电压钳位，因此必须采用电流控制方式。电能质量的相关国内和国际标准要求并网逆变器馈入电网的电流接近正弦波，且各次谐波在一定范围内。同时，为了能够控制逆变器向电网馈送的功率，就必须首先准确地检测出电网电压的相位。通常采用锁相环（Phase-Locked Loop, PLL）跟踪单相电网的基波分量或三相电网的基波正序分量的相位来确定电网电压的相位角。由于并网逆变器的电流基准是利用锁相环的输出相位信息生成的，当锁相环输出的相位信息存在脉动时，会导致电流基准的波形畸变，进而影响入网电流波形，无法满足电能质量的标准；更严重的是，当锁相不准确时，可能导致入网电流反向，造成能量回灌，使逆变器母线电压升高，并使逆变器开关器件承受过大的电压应力而损坏。因此，锁相环的性能在并网逆变器的控制中起到至关重要的作用。

在三相系统中，锁相环的目标是快速准确地得到三相电网电压的基波正序分量。目前较常采用的方法是同步旋转坐标系法（Synchronous Reference Frame PLL, SRF-PLL），该方法通过坐标变换将三相电压变换到 dq坐标系，并通过控制 q轴上的电压uq为零来实现锁相。当三相电网电压为理想时，该方法可以快速准确地得到锁相结果。但是当三相电网电压发生畸变时，三相电压中会存在基波负序分量、零序分量和谐波分量，它们会在uq中引入不同频率的脉动，进而造成锁相误差。虽然可以通过降低控制环路带宽的方法来抑制脉动，但由于其最低频率是由基波负序分量引起的两倍工频，因此要将锁相环的带宽取得很低才能取得较好的脉动抑制效果，这将会严重影响系统的动态性能。所以同步旋转坐标系法在三相电网电压存在畸变时，无法兼顾稳态性能和动态性能[1,2]。

为了提高在非理想电网下锁相环的性能，国内外许多学者进行了大量的研究。为了消除基波负序分量造成的低频脉动，文献[3,4]提出了解耦的双旋转坐标系法（Decoupled Double Synchronous Reference Frame PLL, DDSRF-PLL）。该方法通过双旋转坐标系将正负序分量进行分离并消除了负序分量，对于不平衡的三相电网有着很好的锁相效果。但对低次谐波分量引起的相位脉动，该方法仍然需要通过降低锁相环的带宽来抑制，因此其动态性能依然受到限制。文献[5,6]提出了基于广义二阶积分环节的锁相环（Second Order Generalized Integrators, SOGI），它首先采用带通滤波器滤除三相电压中的谐波成分，再通过对称分量法对基波分量进行分解，在得到基波正序分量后再锁相。该方法的主要难点是带通滤波器Q值的选取：若Q值高，则滤波器的选择能力强，即只允许基波分量通过，对谐波的衰减能力强，但这也使得锁相环的鲁棒性变差，同时也降低了其动态性能；如果Q值低，鲁棒性和动态性能好，但对低次谐波的衰减能力差。因此仍然需要在稳态性能和动态性能之间做出折中。文献[7-9]提出了基于串联信号延迟对消法的锁相环（Cascaded Delayed Signal Cancellation PLL, CDSC-PLL），其主要思想是利用延时半个周期的正弦信号与原信号叠加能够正负抵消的特性，来消除由于基波负序分量以及谐波分量在uq中引起的脉动。文中提出的延时对消算子（Delayed Signal Cancellation Operator,DSCn）本质上是一个周期性的陷波滤波器，可以一次滤除多个频率的谐波，大大简化了算法，与其他锁相方法相比有着较大的优越性。但文献[7-9]中对于所有谐波都采用延迟对消算子来滤除，当谐波次数较多的时候，其实现方案仍然较为复杂。本文在此基础上对延迟对消算子进行了优化选择，在保证系统锁相精度和动态性能的前提下减少了延迟对消算子的数量，从而减少了延迟时间，简化了锁相算法。

上述文献主要着眼于消除三相不平衡和低次谐波对锁相造成的影响，而忽略了高次谐波。而随着新能源发电装置接入电网的容量越来越大，电网中高次谐波的影响也不可忽略[10]，因此本文在串联信号延迟对消法的基础上，提出了一种二型三阶的调节器，该调节器与传统的调节器相比，对高次谐波的抑制能力大大增强了。同时，由于该调节器的参数较多，通过传统试凑的方法很难得到一个优化的结果。针对这一问题，本文还提出了一种根据系统相位裕度和谐波抑制要求直接计算出调节器参数的方法，避免了反复试凑。

本文首先建立了同步旋转坐标系法的数学模型，说明了该方法在三相畸变电网下存在锁相误差的原因。然后介绍了延迟对消算子消除谐波的原理并优化选择了延迟对消算子。为了消除高次谐波对锁相造成的影响，本文接着提出了一种二型三阶的调节器，并给出了一种根据系统相位裕度和谐波抑制要求直接计算出调节器参数的方法，同时给出了闭环设计实例。最后通过实验验证了理论分析的正确性和闭环设计的有效性。本文提出的二型三阶调节器和闭环设计思路同样也可以应用到别的锁相算法中去。

2 同步旋转坐标系法

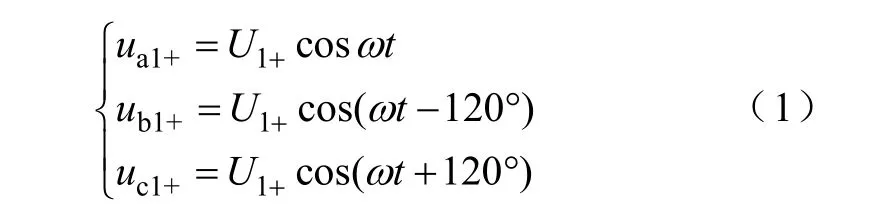
首先分析三相电网电压为理想时的情况，此时电网电压只含有基波正序分量。其时域表达式为式中，ω是电网电压的角频率。令θ=ωt，显然，由于三相对称，只要求出 a相电压的相角 θ，即可很容易地求出其他两相电压的相角。

对于三相电网电压，一种更直观的表示方法是通过abc坐标系下的综合矢量来表示。综合矢量定义为

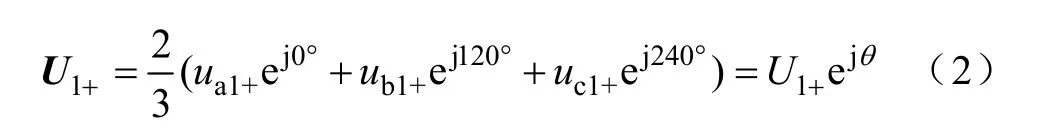
由式（2）可以看到，综合矢量是一个以U1+为模，以角速度ω逆时针旋转的旋转矢量。如图1所示。从图中可以看到，要得到的相角θ就是综合矢量 U1+与 a轴的夹角。尽管 θ是客观存在的，但是无法通过直接的方法得到 θ，因此常用的方法是通过abc到dq坐标变换构造一个与综合矢量旋转角速度相同的dq坐标系，如图2所示。此时该综合矢量相对于dq坐标系静止，当综合矢量的相角θ与dq坐标系的相角θ1相同时，综合矢量在q轴上分量uq为零。所以可以通过控制uq为零来实现锁相。

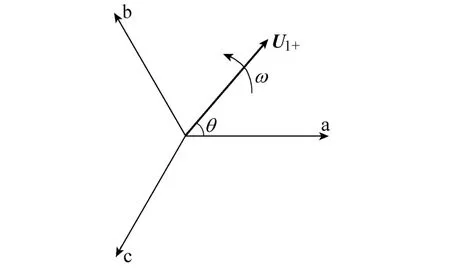
图1 abc坐标系及综合矢量U1+Fig.1 abc frame and rotating voltage vector U1+

图2 abc到dq坐标系变换Fig.2 abc to dq transformation

坐标变换具体实现分为两步，分别为abc到αβ变换和αβ到dq变换，其变换矩阵分别为

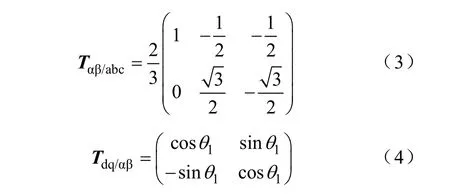
当三相电网电压为理想时，其经过abc到dq变换得到的电压uq和ud为

该结果也可以从图2中直观地看出，而当锁相成功时，有θ=θ1，则uq=0，在实际物理实现时需要通过控制uq为零来实现锁相，则控制框图如图3所示。图中虚框部分是校正环节，为了保证整个环路是负反馈，需要在校正环节中加一个–1。

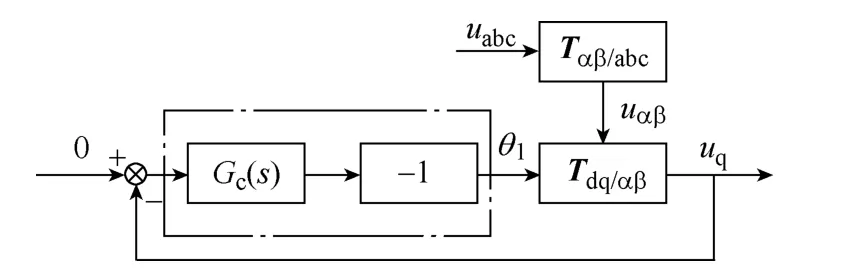
图3 系统的控制框图Fig.3 Block diagram of the system

上面的讨论均是基于三相电网电压为理想这一前提，而实际中三相电网电压存在着不同程度的畸变。三相电网电压的畸变主要表现为三相电压不平衡、存在谐波。在此首先讨论不平衡的情况。

根据对称分量法，不平衡的三相电压可以分解为正序、负序和零序分量。由于零序分量可以被坐标变换所消除，对锁相不会造成影响，因此在此仅考虑负序分量。基波负序分量的时域表达式为

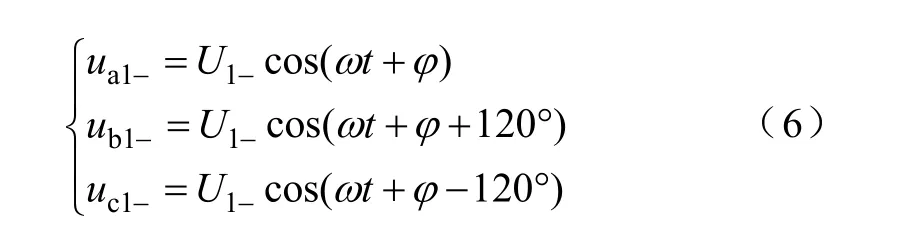
当存在负序分量时，综合矢量除了逆时针旋转的基波正序分量外，还有顺时针旋转的基波负序分量，如图4所示。从图中可以看出，该负序分量相对于dq坐标系是以2ω的角频率顺时针旋转的，因此变换到 dq坐标系中会在 uq中引入 2ω的交流分量。具体表达式为

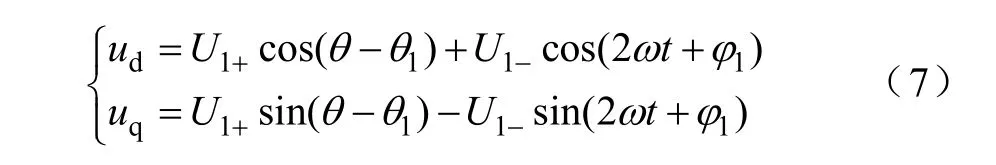
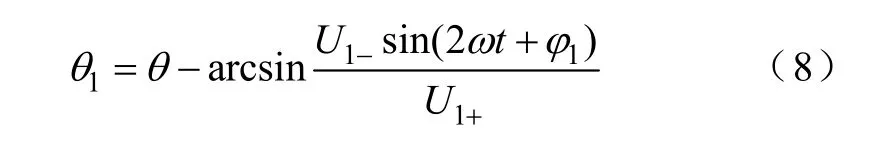
可见，输出相角θ1中含有两倍工频的交流脉动，显然，θ1≠θ。

同理，对于存在谐波时做同样的分析可以得到类似的结果：h次谐波正序分量会在uq中引入角频率为(h-1)ω 的交流分量，h次谐波负序分量会在uq中引入角频率为(h+1)ω 的交流分量。此时同样无法通过直接控制uq为0来实现锁相。

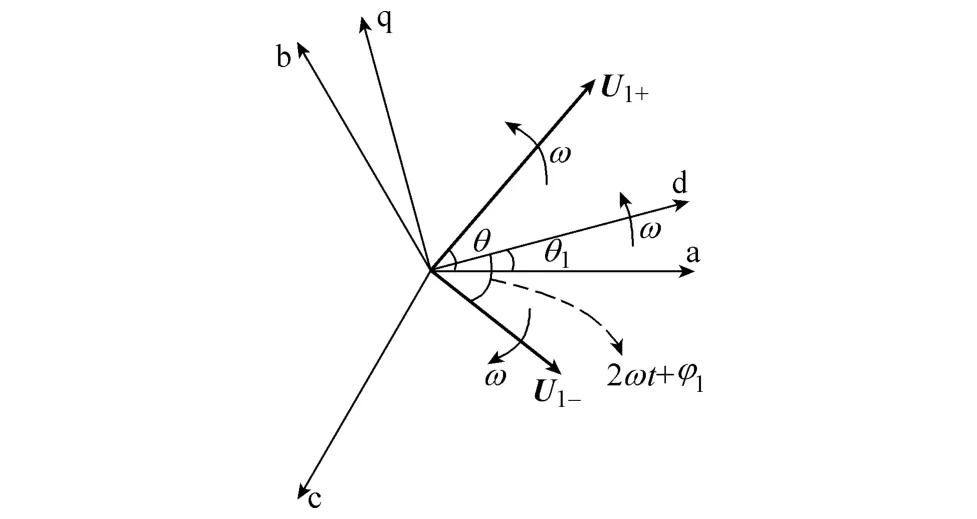
图4 存在基波负序分量的abc到dq变换Fig.4 abc to dq transformation with fundamental negative-sequence component

从上面的分析可以看出：当电网电压存在畸变时，电压综合矢量通过坐标变换变换到 dq坐标系后，uq不再是直流量，而是直流量叠加上不同频率的交流分量，而这些交流分量是造成锁相偏差的主要原因。虽然可以通过降低控制环路的带宽来抑制这些交流分量，但由于交流分量中的最低频率是基波负序分量引入的两倍工频（即100Hz），因此需要将锁相环的带宽设置得非常低（10Hz以下）才能取得比较好的抑制效果，而这势必会大大降低系统的动态性能。

3 串联信号延迟对消法

由上节的讨论可知，通过降低带宽的手段来抑制uq中的交流量会影响系统的动态性能。而本节将讨论的串联信号延迟对消法则是一种在不降低系统带宽的前提下抑制基波负序分量和谐波分量的方法。基于这种方法来设计的锁相环在其动态性能和稳态性能均达到令人满意的效果。

3.1 延迟对消算子的原理

延迟对消算子的本质思想是：对于一个直流量中叠加了交流量的信号，将该信号延迟特定的时间与原信号相加再除以 2就可以消除其中的交流信号，而对直流量的大小没有影响。如图5所示，具体的延迟对消算子的数学表达式为

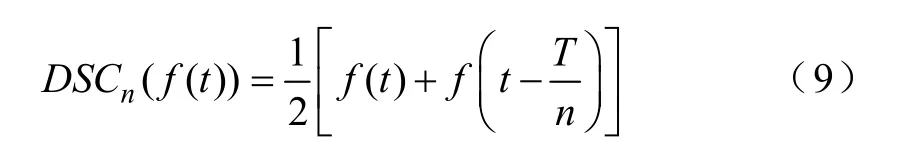
图5 信号延迟对消算子消除信号中的交流分量Fig.5 Demonstration of how DSC operator eliminates the AC component in the signal

uq中的脉动是不同频率的交流量的叠加，对于其中特定频率的交流量，可以写成

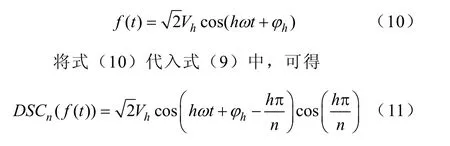
为了用 DSCn算子消除该次谐波，即DSCn(f(t))=0，显然只要cos(hπ/n)=0，即

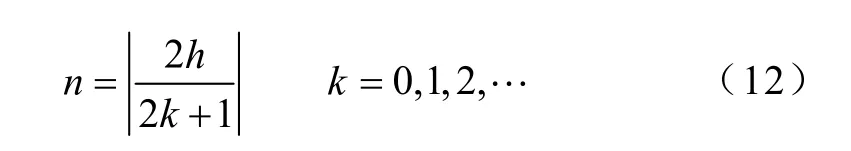
对于特定的h次谐波，根据式（12）可以解出合适的延迟系数n，即可通过DSCn算子来消除该次谐波。

3.2 延迟对消算子的优化选择

对于三相电网电压而言，谐波一般为 6k±1次（k=0, 1, 2, …, n）[11]。由3.1节的讨论可知，对于每一次谐波，都可以根据式（12）计算出所需要的延迟系数 n，具体结果见表 1（谐波抑制考虑到 41次），其中h(abc) 表示在abc坐标系下的谐波次数，h(dq) 表示相应变换到dq坐标系下的谐波次数。从表1可以发现，由于正弦信号的周期性，一个DSCn算子可以消除多次谐波，所以没有必要每次谐波都配备一个DSCn算子，这就大大减少了需要的DSCn算子的数目。

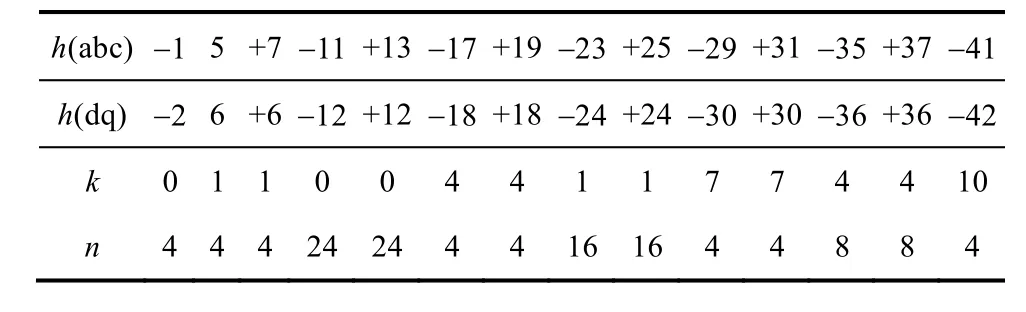
表1 消除各次谐波所需要的延迟环节Tab.1 The DSC operators needed to eliminate harmonics

当电网电压发生畸变时，如果完全用信号延迟对消算法来消除uq中的交流量，需要的信号延迟对消算子分别为：DSC4、DSC8、DSC16和 DSC24[7-9]。实现该算法所需要的延时为 T/4+T/8+T/16+T/24≈0.5T=10ms，其延时时间较长，程序所占用的存储空间也较大。

进一步观察表1可以发现，如果用信号延迟对消算法消除 uq中 18次以下的脉动，只需要 DSC4和DSC24两个算子即可。而18次以上的脉动属于高次谐波，完全可以通过控制环路本身来滤除，而对系统的动态性能影响不大。综合系统动态性能和算法实现复杂度的考虑，本文采用 DSC4和 DSC24两个算子串联消除uq中18次以下的脉动，18次以上的脉动则通过设计控制环路来滤除。则控制框图如图6所示。此时算法所需要的延时约为5.8ms，与文献[9]中的方案相比减少了延时，同时也简化了程序。

图6 加入串联延迟对消算子后的控制框图Fig.6 Block diagram of system with DSC operators

由于信号延迟对消算子中存在延时环节，在控制环路中会引入相角的滞后，会对控制环路的设计带来不利的影响。为了避免这种影响，可以将信号延迟对消算子等效地变换到αβ坐标系中[9]，即

变换后的等效控制框图如图7所示，此时信号延迟对消算子起到了一个前置滤波器的作用，可以有效地消除电网电压不平衡和存在低次谐波对锁相造成的偏差，并且对控制环路的相位裕度没有影响。

图7 将延迟对消算子变换到αβ坐标系中的控制框图Fig.7 Block diagram of system with DSC operators transformed into αβ frame

4 控制环路的设计

4.1 二型三阶调节器的提出

当三相电网电压为理想时，有 uq=U1+sin(θ-θ1)，当系统进入稳态，有 θ≈θ1，则 uq=U1+sin(θ-θ1)≈U1+(θ-θ1)，可以将图3进行线性化为图8。

29个不同品种的枣叶均采集于新疆阿拉尔市(东经81°17′41. 61″，北纬40°32′23. 50″)塔里木大学园艺试验站红枣资源圃内多年生的枣树叶片(见表1)，经植物科学学院吴翠云教授鉴定为鼠李科枣属植物叶片。采集时间为2016年6月，采集的样品经50℃干燥恒重后粉碎，过40目筛，密封，室温储藏备用(已留样保存)。

图8 线性化后的的控制框图Fig.8 Linearized block diagram of system

而锁相的本质是要求输出相角θ1无静差地跟踪电网电压的相角 θ，为了使得控制环路的物理意义更为明确，以θ为输入，θ1为输出对图8所示的方框图进行等效变换，可以得到图9。

图9 控制框图8的等效变换Fig.9 Equivalent block diagram of Fig.8

由于θ(s) 是从0线性上升到2π，再回到0，如此周期反复。可认为θ(s) 是斜坡函数，要对斜坡函数进行无静差跟踪，则 Gc(s) 必须是二型系统，传统的调节器设计方法是将Gc(s) 设计为一个PI调节器加上一个积分环节[12,13]，即

而当三相电网电压非理想的时候，虽然可以通过串联信号延迟对消算子消除电压不平衡和低次谐波对锁相造成的偏差，但电网电压的高次谐波仍然需要通过控制环路本身来滤除。而传统的调节器如式（14）所示，在高频处是-20dB/10倍频程下降的，对高次谐波的抑制能力较差，为了提高调节器对高次谐波的抑制能力，本文对调节器进行了改进，在高频处加入一个极点，如式（15）所示。

图 10给出了加入高频极点和未加入高频极点的调节器的伯德图对比。

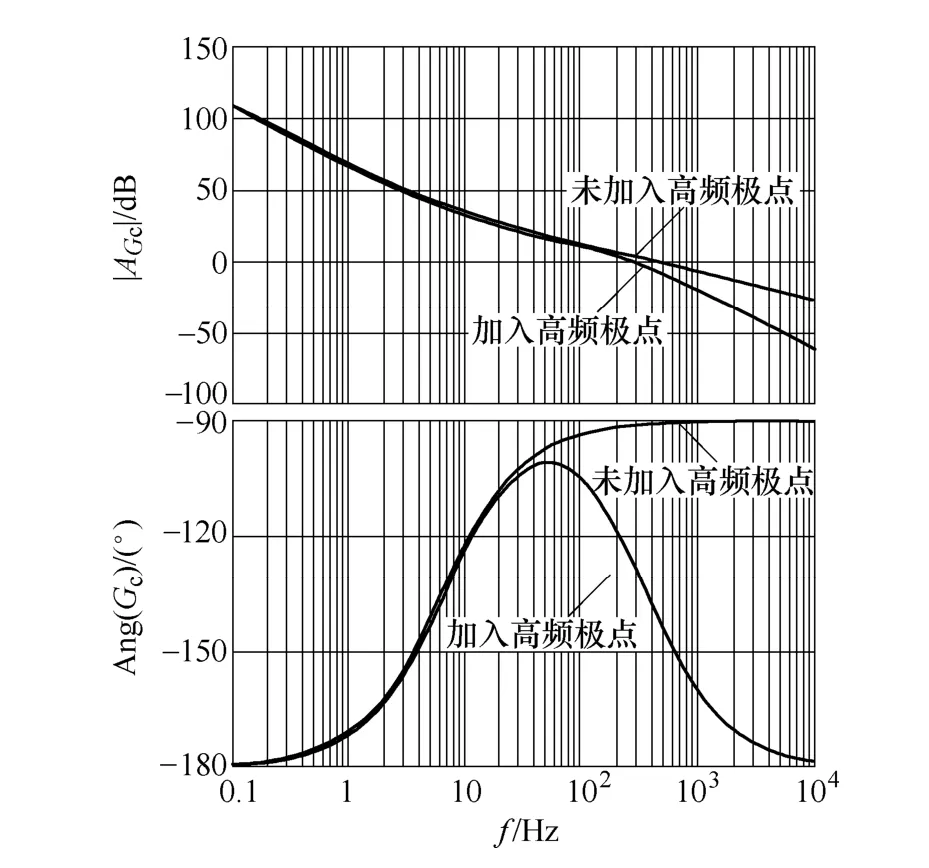
图10 调节器的伯德图Fig.10 Bode diagram of the controller

从图10可以看出，当在调节器中加入高频极点后，系统在高频处是-40dB/10倍频程下降的，对高次谐波的抑制能力大大增强了，但加入极点的同时也会对系统相位裕度造成恶劣的影响。在实际设计调节器时，调节器本身参数较多且互相影响，而人们既希望其对高次谐波有较强的抑制能力，又希望其能有足够的相位裕度，同时还希望系统的带宽能尽量高以获得较好的动态性能。而通过传统的参数试凑的设计方法很难同时满足这些要求，下面就给出一种调节器参数的设计方法，根据系统的性能指标要求进行相应的计算，直接得出一个优化的结果，避免了反复试凑。

4.2 调节器参数设计的详细步骤

从式（15）可以看出，Gc(s) 包含三个环节：积分环节1/s，PI环节Kp+Ki/s以及一阶低通滤波环节1/(T1s+1)。图11给出了这三个环节的伯德图。

PI调节器的转折频率为 fL1和一阶低通滤波环节的转折频率为fL2分别为

图11 Gc(s) 三个环节的伯德图Fig.11 Bode diagram of three components in Gc(s)

先讨论PI调节器的转折频率fL1和Gc(s) 截止频率 fc的关系。若fL1＞fc，则在截止频率fc处，PI调节器引入的负相移大于 45°，而积分环节的相角始终是-90°，同时一阶低通滤波环节的相角始终是负的，那么系统的相位裕度一定小于 45°。所以要保证相位裕度大于45°时，必须按照fL1＜fc来设计。

因为 fL1＜fc，而 Ki对高于 fL1频率段的系统的幅频特性影响很小，所以在截止频率处PI调节器可以近似为一个比例环节Kp。由于在截止频率处系统环路增益幅值为1，由式（15）可得

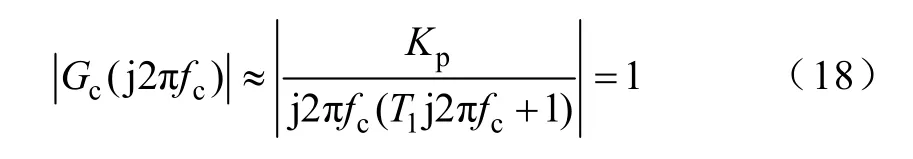
为了通过控制环路来滤除高次谐波，则该控制环路对高次谐波的增益是有要求的，假设要求该系统对电网电压h次谐波增益小于a%，则有

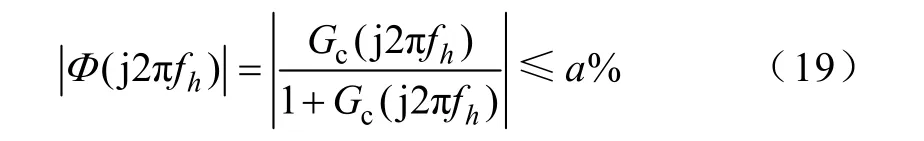
最后，对于一个控制系统，根据相位裕度的要求，则有

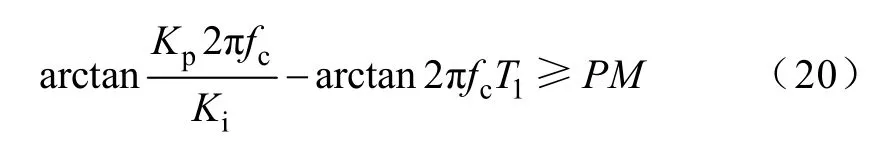
将式（18）代入式（19），可以得到T1的取值下限，即

由式（20）和式（24）可以知道：尽管系统的相位裕度由T1、fc、Kp和Ki共同决定，但T1的取值有一个上限，当T1的取值超过由式（24）所确定的上限时，无论怎样设计fc、Kp和Ki都不可能满足系统的相位裕度要求。

由式（21）和式（24）可以画出T1和fc的可选域，如图12所示（相关参数在第4.3节给出）。图12的物理意义是很明确的，T1越大，一阶低通滤波环节的转折频率fL2就越小，控制环路对高次谐波的抑制能力就越强，相应地，在截止频率处引入的负相移也越大，系统的相角也会更恶劣。所以要在相位裕度和谐波抑制能力之间做一个权衡。又因为希望系统的动态响应速度快，所以在满足相位裕度和谐波抑制约束要求的前提下，fc取越大越好。

由图 12可以确定 T1和 fc，再根据式（18），可以解出Kp，即

Ki越大，系统低频增益越大，稳态性能越好，但相应地PI调节器的转折频率越大，在截止频率处引入的负相移也越大，系统的相位裕度就越小。本文设计的原则是在满足相位裕度的前提下 Ki取越大越好。

4.3 设计实例

上面给出了控制环路设计的详细步骤，下面根据本文的具体参数，给出一个设计实例。本文设计控制环路时，综合动态性能和稳态性能的要求，取PM=45°。根据表1可知，从24次谐波开始以后的高次谐波需要用控制环路本身来滤除，所以取fh=24f =1 200Hz，同时取 a%=10%。由式（21）和式（24）可以画出T1和fc的可选域，如图12所示。

图12 T1和fc的可选域Fig.12 The possible region of T1 and fc

因为希望系统有较快的动态响应，所以在满足相位裕度和谐波抑制约束要求的前提下，fc取越大越好。根据图 1 2，取 fc=300Hz，T1=4.8×10-4。根据式（25）可以求出Kp=2.77×103。根据式（26）可以求出1 .13× 1 05，由于Ki越大，低频增益越大，系统的稳态性能越好，所以在此取Ki=1.13×105。

根据以上控制参数，可以画出Gc(s) 的伯德图，如图13所示。对设计出的Gc(s) 进行校核，计算得出 Gc(s) 的相位裕度为 46.6°，闭环传递函数在 24次谐波处的增益为 10.8%，与设计指标相比较，误差较小，可以看出本文提出的设计方法可以快速准确地得到满足设计要求的闭环参数而不需要反复试凑。

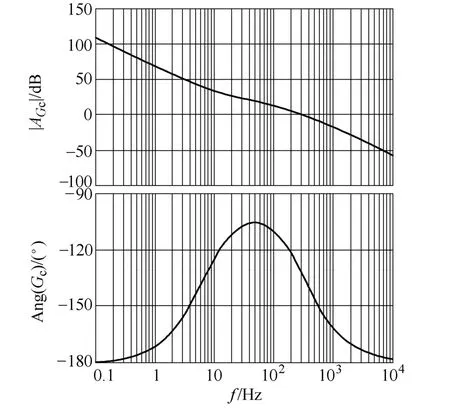
图13 设计调节器的伯德图Fig.13 Bode diagram of the designed controller

5 实验验证

为了验证上述理论分析的正确性和闭环设计方法的有效性，在实验室搭建了硬件平台进行了实验验证。系统的硬件框图如图14所示，即三相电网电压经过调理电路，由A-D采样后送入DSP，在DSP中进行锁相运算，最后通过D-A输出锁相结果。其中电压检测采用电压霍尔 HNV025A，A-D采用Maxim公司的 max1324,DSP采用 TI公司的TMS320F2812，D-A采用DAC7624。通过AC source（Chroma 6590）来产生畸变的三相电网电压。

图14 系统硬件结构框图Fig.14 Block diagram of the prototype

图15给出了三相电压不平衡时的锁相结果，实验参数如下：Ua:1pu(0°)，Ub:1(pu)(-190°)，Uc:0.2(pu)(-240°)。从图 15中可以看到，当三相电网电压不平衡时，基波负序分量会在uq中引入二倍基波频率的脉动。对于同步旋转坐标系法，在不降低带宽的情况下是无法抑制该脉动的，最终会在输出的相角中反映出两倍工频的脉动，使得锁相输出有很大误差。而加入了信号延迟对消算子后，由于其对uq中的二倍工频脉动有很强的抑制能力，最终输出相角可以很好地跟踪基波正序分量的相角。

图15 三相电压不平衡的实验结果Fig.15 Experimental results with grid voltage unbalanced

图16给出了电网电压存在谐波时的锁相结果，为了验证所提出的二型三阶调节器能有效地抑制高次谐波对锁相的影响，在实验中特意加大了高次谐波的含量。具体实验参数见表 2。从实验结果可以看出：未加入一阶低通滤波环节时，尽管串联延迟对消环节对低次谐波抑制能力较强，但由于锁相环路对高次谐波抑制能力较差，使得输出相角θ中会含有高频的脉动，从而导致进网电流参考iref中也会含有高频的脉动，进而会影响入网电流质量。而加入了一阶低通滤波环节后，大大加强了对高次谐波的抑制能力，进而可以得到理想的锁相结果。

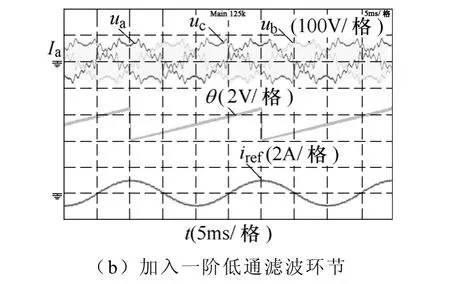
图16 三相电压存在谐波情况下的实验结果Fig.16 Experimental results with grid voltage consists of harmonic components

表2 三相电压存在谐波时实验参数Tab.2 Experimental parameters of grid voltage consists of harmonic components

图17给出的是锁相环动态实验，图17a给出的是电网电压下跳实验，在10ms时，Uc的电压从1(pu)下跳至0.2(pu)，图17b给出的是电网电压上跳实验，在30ms时，Uc的电压从0.2(pu)上跳至1(pu)。从实验结果可以看出：由于基于串联信号延迟对消法设计的锁相环通过算法来消除低次谐波，因此控制环路的带宽可以做得较高，动态响应也较快，从实验上来看约为10ms左右。

图17 锁相环动态实验结果Fig.17 Experimental results of the dynamic performance of the PLL

6 结论

本文通过优化选择延迟对消算子消除了三相电压不平衡和低次谐波对锁相的影响。在此基础上，提出了一种二型三阶的调节器来消除电网电压中的高次谐波。同时也给出了基于系统相位裕度，谐波抑制要求的闭环参数设计方法，采用该方法可以根据系统的性能指标快速准确地计算出优化的闭环参数，而不需要反复试凑。最后通过实验验证了理论分析的有效性。本文提出的二型三阶调节器和闭环设计思路同样也可以应用到别的锁相方法中。

[1] Chung S K. Phase-locked loop for grid-connected three-phase power conversion systems[J]. IEE Proceedings-Electric Power Applications, 2000, 147(3):213-219.

[2] Blaabjerg F, Teodorescu R, Liserre M, et al.Overview of control and grid synchronization for distributed power generation systems[J]. IEEE Transactions on Power Electronics, 2006, 53(5):1398-1408.

[3] Rodríguez P, Pou J, Bergas J, et al. Decoupled double synchronous reference frame PLL for power converters control[J]. IEEE Transactions on Power Electronics, 2007, 22(2): 584-592.

[4] 王颢雄, 马伟明, 肖飞, 等. 双 dq变换软件锁相环的数学模型研究[J]. 电工技术学报, 2011, 26(7):237-241.Wang Haoxiong, Ma Weiming, Xiao Fei, et al. Study of model of software phase locked-loop basedon dual-dq synchronous transform[J]. Transactions of China Electrotechnical Society, 2011, 26(7): 237-241.

[5] Rodriguez P, Luna A, Ciobotaru M, et al. Blaabjerg.Advanced grid synchronization system for power converters under unbalanced and distorted operating conditions[C]. In Proc. 32nd Annunnal Conference IEEE Industry Electronics, 2006, 5173-5178.

[6] Pedro Rodríguez, Alvaro Luna, Ignacio Candela, et al.Multiresonant frequency-locked loop for grid synchronization of power converters under distorted grid conditions[J]. IEEE Transcations on Industrial Electronics, 2011, 58(1): 127-138.

[7] Francisco A S Neves, Marcelo Cabral Cavalcanti,Helber Elias Paz de Souza, et al. A generalized delayed signal cancellation method for detecting fundamental-frequency positive-sequence three-phase signals[J]. IEEE Transcations on Power Electronics,2010, 25(3): 1816-1825.

[8] Wang Yifei, Li Yunwei. Analysis and digital implementation of cascaded delayed-signal-cancellation PLL[J]. IEEE Transcations on Power Electronics,2011, 26(4): 1067-1080.

[9] Wang Yifei, Li Yunwei. Grid synchronization PLL based on cascaded delayed signal cancellation[J].IEEE Transcations on Power Electronics, 2011, 26(7):1987-1997.

[10] 王学华, 阮新波, 刘尚伟．抑制电网背景谐波影响的并网逆变器控制策略[J]．中国电机工程学报,2011, 31(6): 7-14.Wang Xuehua, Ruan Xinbo, Liu Shangwei. Control strategy for grid-connected inverter to suppress current distortion effected by background harmonics ingrid voltage[J]. Proceedings of the CSEE, 2011,31(6): 7-14.

[11] Timothyl. Skvarenina. The power electronics handbook[M]. Florida: CRC Press, 2002.

[12] Guo Xiaoqiang, Wu Weiyang, Chen Zhe, Multiplecomplex coefficient-filter-based phase-locked loop and synchronization technique for three-phase gridinterfaced converters in distributed utility networks[J].IEEE Transcations on Power Electronics, 2011, 58(4):1194-1204.

[13] Helber E P de Souza, Fabrício Bradaschia, Francisco A S Neves, et al. A method for extracting the fundamental frequency positive sequence voltage vector based on simple mathematical transformations[J]. IEEE Transcations on Industrial Electronics, 2009,59(5): 1539-1547.