基本药物配送路径优化新思路——基于山西省X物流公司的实证研究

闫娟娟，李瑞风（山西中医学院，山西 太原 030024）

1 研究背景

作为深化医药卫生体制改革的五项重点工作之一，国家基本药物制度包括药品生产、流通、使用、价格管理、报销等内容。为了发挥基本药物“保基本、重基层、强基础”的作用，配送成为关键环节。按照基本药物制度规定，基本药物实行“以省为单位、公开招标、统一配送”，即招标确定基本药物配送企业，生产企业要么直接配送基本药物，要么委托具有现代物流能力或具备相应条件的药品经营企业配送。随着基本药物制度推进的深入，各省出台了相应的基本药物配送制度，如上海松江模式、北京社区医药配送模式、浙江社区医药服务共同体配送模式等。但是各省在基本药物配送参与模式、配送权的委托、月采购次数及配送到位时间、药款集中支付周期等方面存在很大差异[1]，并出现了受限于配送利益低而致使医药商业公司配送动力不足以及配送企业能力低无法保障基本药物的需求和质量的现象[2]。因此，结合各省当前配送实际情况，降低配送成本，减少配送环节，完善各省配送模式，保证国家基本药物保质保量及时送达基层医疗卫生机构成为研究的关键问题。

依据《山西省基本药物配送管理办法》，山西省的基层医疗机构及村卫生室使用的基本药物实行省级网上集中采购和统一配送。但是在药品经营企业实际配送中，配送利润的高低往往成为制约医药物流企业基药配送效率的关键因素。因此，有效削减配送企业的基药配送成本、提高其配送利润，将大大提高企业基药配送的速度和积极性，避免众多配送企业“踢皮球”现象的产生。

2 提出问题

以山西的某家医药物流企业X为例，研究它在山西省某一区域的基药物流配送情况。经实际调研，取样配送区域如图1所示。

现以基药的件数（箱）为基本数量单位，根据企业的历史数据得知基药的月均配送量为2 830件，而配送区域各地区的月均需求量相差悬殊，分布极不均衡，具体见表1。

表1 地区基药月均需求分布表

基药配送仓库距离该区域8个地区的距离如表2所示。

表2 仓库—地区距离表

X企业为节省配送的资源和成本，欲在上述地区中选择3个中间站进行一次配送，后续再由中间站对周边地区进行二次配送。对于中间站的选择，方案计划选择文水、孝义和太谷。我们将研究如何选择配运量和路径，构成的基药配送方案将达到最优。

考虑到配送中车型分大货（每次200件）和小货（每次100件），一次配送有两种情况：一为文水配货800件、孝义1 500件、太谷530件；另一为文水配货1 200件、孝义1 300件、太谷330件；而二次配送则由这3个地区再配送给该区域内的8个地区（中间站包含在内），各地区均可相互通达。

根据距离、油耗、人工、仓储等因素，综合的基药配送通达单位成本如表3所示。

表3 基药配送的单位成本表

3 建模求解

考虑到一次配送有两种情况，分别建立配需平衡成本表。

情况1（表4）：

表4 配需平衡成本表（一）

情况2（表5）：

表5 配需平衡成本表（二）

分别用Mi（i=1,2,3 ）和Nj（j=1,2,…,8）表示3个中间站和8个需求地区；

Dj（j=1,2,…,8）分别表示Nj所对应需求量；Si（i=1,2,3 ）分别表示Mi所对应的配运总量；

cij（i=1,2,3;j=1,2,…,8 ）表示把基药从Mi运到Nj的单位成本；

设 xij（i=1,2,3;j=1,2,…,8 ）表示从Mi运到Nj的配运量，f表示配运方案对应的成本，建立模型[3]，则目标函数表示为：minf

在这里，xij≥0,（i=1,2,3;j=1,2,…,8）

（1）对情况1进行配运优化

根据表4，求得初解为：x11=89,x12=711,x21=278,x23=146,x24=1 067,x25=9,x31=49,x36=194,x37=73,x38=214,依次求检验数，可得 x13、x14、x15、x16、x17、x18的检验数分别为 18、26、26、34、44、44；x22、x26、x27、x28的检验数分别为 0、8、20、28；x32、x33、x34、x35的检验数分别为 6、16、16、12。

由于所有的检验数都大于等于零，故初解所对应的配送量即为表4的最优解[4]。

经过调研，由于一次配送时采取的是集中模式，其单位成本将比二次配送少50%。情况1的一次配送成本为f1=7.5×800+14×1 500+5×530=19 650，二次配送成本为 f2=3×89+16×278+4×146+2×9+22×49+10×194+4×73=8 627。

情况1的基药配送综合成本为f=f1+f2=29 650+8 627=38 277。

（2）对情况2进行配运优化

根据表5，求得初解为：x11=416,x12=711,x16=73,x23=146,x24=1 067,x25=9,x26=78,x36=43,x37=73,x38=214，依次求检验数，可得 x13、x14、x15、x17、x18的检验数分别为－8、0、0、10、10；x21、x22、x27、x28的检验数分别为 26、26、12、20；x31、x32、x33、x34、x35的检验数分别为 34、40、24、24、20。

由于存在检验数－8＜0，表明初解所对应的配送量并非最优解，在闭回路x13→x16→x26→x23→x13中选择调运量min｛ x16,x23｝=73[5]，得到的新解为：x11=416,x12=711,x13=73,x23=73,x24=1 067,x25=9,x26=151,x36=43,x37=73,x38=214。

依次求得检验数，可得x14、x15、x16、x17、x18的检验数分别为8、8、8、18、18；x21、x22、x27、x28的检验数分别为18、18、12、20；x31、x32、x33、x34、x35的检验数分别为 26、32、24、24、20。

此时所有的检验数都大于等于零，故新解所对应的配送量即为表5的最优解。

情况 2 的一次配送成本为 f1=7.5×1 200+14×1 300+5×330=28 850，二次配送成本为 f2=3×416+9×73+4×73+2×9+12×151+10×43+4×73=4 749。

情况2的基药配送综合成本为f=f1+f2=28 850+4 749=33 599。

显然，选择情况2的配送模式、配运量和路径，构成的基药配送方案将达到最优，成本节省13.92%。

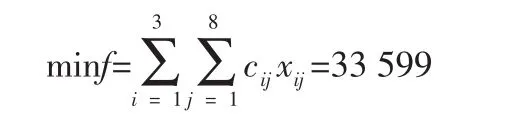
此时基药配运的最优方案为：

X企业基药配送仓库首先进行一次配送，即分别向中间站文水配送基药1 200件、孝义配送1 300件、太谷配送330件。中间站进而继而进行二次配送，具体路径为：文水站点留下711件，再向交城和汾阳分别配送416件、73件；孝义站点留下1 067件，再向汾阳、介休和平遥分别配送73件、9件和151件；太谷站点留下214件，再向平遥和祁县分别配送43件、73件。具体如图2所示。

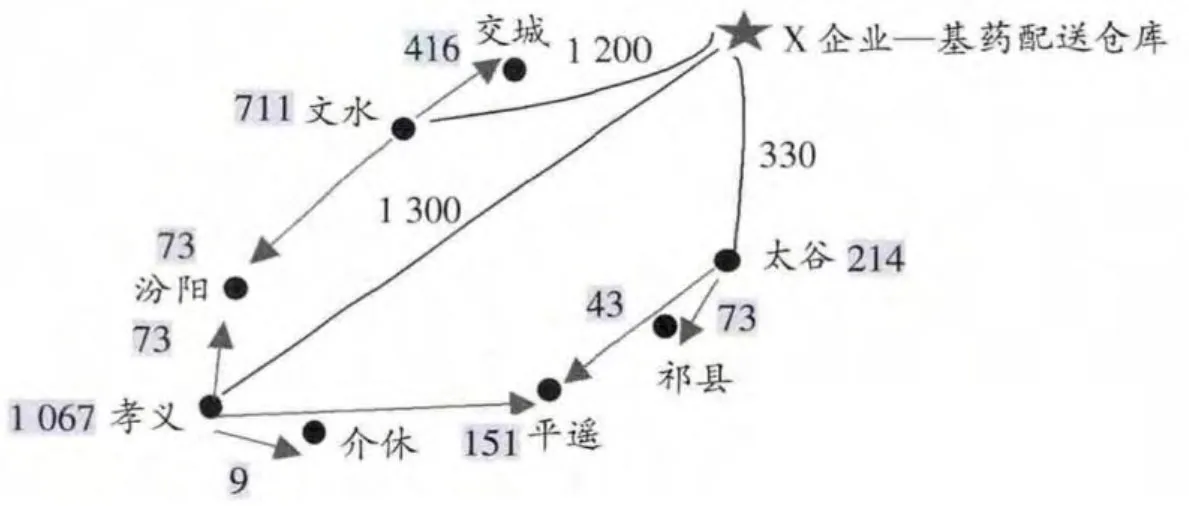
图2 最优配送路径分布图

4 结束语

本研究对基药配送中利益导向的物流企业进行了配送路径优化，运输模型在中间站二次配运路径中的应用实现了成本的最优化，结果表明节省13.92%配送成本。值得提出的是，研究数据来源于实际的调研，对于基药配送物流企业的成本、利润改善及配送及时性都有很好的实际意义。研究中，基药配送通达单位成本的核算虽然涵盖了距离、油耗、人工、仓储四项成本，数据来源于调研企业的具体核算，实际中可能还存在其他一些成本，在这里未能包含在内，因此，参考本研究的配送优化方法时，须要结合实际情况。

[1] 杨林，吴逢波，杨敏,等.全国各省基层医疗卫生机构基本药物统一配送实施方案比较研究[J].中国药房，2012(20):1845－1846.

[2] 焦婷婷，冯泽永.基本药物配制配送环节影响因素分析及对策[J].中国药房，2012(16):1474－1476.

[3] 韩伯棠.管理运筹学[M].3版.北京：高等教育出版社，2010:127－128.

[4] Dror M,Laporte G,Trudeau P.Vehicle Routing with Split Deliveries[J].Discrete Applied Mathematics,1994,50(3):239－254.

[5] Wang Zhufang,Miao Wenqing.An Improved Algorithm to Solve the Transportation Problems of Relief Materials[C]//Proceedings of the 29th Chinese Control Conference.Beijing,China,2010:1742－1746.