热带太平洋上层洋流异常的复EOF分析

卢姁，包赟，吕庆平

（1.中国人民解放军61741部队，北京 100094；2.中国人民解放军东海舰队海洋水文气象中心，浙江宁波 315122）

1 引言

海洋，尤其是热带海洋，是大气运动的重要能源，对气候变化有着不可忽视的影响。大洋环流既影响海洋热含量的分布，也影响到海洋向大气的热量输送过程。低纬度海洋获得了较多的太阳辐射能，通过大洋环流可将其中一部分输送到中高纬度海洋，然后再提供给大气。前人对热带太平洋海洋状态的异常多集中在表层温度异常（SSTA）上，并探讨了其与东亚冬、夏季风异常和长江中下游及华北降水、温度异常之间的关系[1]。海洋流场是重要的动力学变量，其地位不亚于海洋温度场；为此对热带太平洋上层洋流异常进行统计动力诊断是很有必要和十分有意义的。在气候诊断方面，EOF分解是常用的方法[2]，该方法可用个数较少的几个模态的叠加来描写原来的气候变量场，且又能基本涵盖原来变量场的信息；在此各模态是相互独立（正交）的，并具有各自的物理意义；故而该方法已获得普遍应用。与通常对标量场（如温度场）EOF分解不同，因水平流场是一个二维向量场，这样对其做统计动力诊断则必须采用复EOF分解，这是由于复数可描写二维向量的缘故；然而复EOF分解要比通常的实EOF分解来得复杂；正因如此，除我们的工作外[3-5]，复EOF分解前人涉及较少。

从北太平洋海域SSTA的EOF分解知，其有两个主要的年代际变化气候模态，分别称为PDO模态（第一模态，其年代际变化周期为约22年）[6]和NP⁃GO模态（第二模态，其年代际变化周期为约13年）[7]；它们也是北太平洋的两个主要气候模态，并对年代际气候异常有重要影响。我们对热带外北太平洋海域的大洋环流异常做过复EOF分解[5]。并发现其流场异常的第一、二模态均有3—7年的年际变化，这是ENSO现象在该海域大洋环流异常上的反映；在年代际变化上，第一、二模态分别有明显的约20年、约18年的周期，第二模态还有较明显的约13年的周期，这分别是PDO和NPGO在该流场异常上的反映。众所周知，ENSO在热带太平洋表现最显著，其具有3-7年的年际变化周期，并与赤道海洋Kelvin波和混合Rossby-重力惯性波关系密切，是气候变化的强信号。我们的工作[5]表明，热带太平洋的EN⁃SO能够对热带外北太平洋的流场异常发生影响。

ENSO除有3—7年的年际变化周期外，还有年代际变化。Di Lorenzo等[8]通过量化太平洋年代际尺度的动力作用，建立了一个太平洋气候变量的概念模型，该模型依赖于海洋年代际变量(PDO,NP⁃GO)，大气强迫(AL,NPO)和ENSO循环以及它们之间的相互联系。PDO和NPGO与ENSO循环的不同阶段有关。春季北部的NPO使热带太平洋中部产生SSTA，并可通过季节足迹机制[9-10]来引发ENSO在下个冬季达到顶峰，然后ENSO通过大气遥相关对AL产生影响，进而影响到PDO、NPO。通过该季节足迹过程，NPO不但可影响东太平洋厄尔尼诺[11]，而且也可改变中太平洋厄尔尼诺[12]。在这个过程中，北太平洋的变化在冬季通过海表面热通量在SST上留下“足迹”，并在海洋中一直储存到夏季；在副热带则可改变包括纬向风在内的大气环流。该环流向南延伸至赤道，进而改变ENSO的年代际变化。由此可知，ENSO的年代际变化与北太平洋主要气候模态PDO、NPGO两者关系密切且相互影响。因此要更好理解PDO、NPGO的动力机制，特别是其年代际变化的机制，则必须要考虑到热带太平洋的作用以及热带与中纬度各大气、海洋系统之间的相互耦合。

为揭示ENSO在热带太平洋流场上的表现，了解其年际和年代际变化的规律，并探索其与北太平洋主要气候模态PDO和NPGO之间的关系；本文采用复EOF分解方法，对全年热带太平洋上层大洋环流异常做了统计动力诊断；给出了其第一、二模态流场异常的空间分布和时间系数，以及其年际、年代际变化的情况，并探讨了这两个模态的性质特点。

2 资料和诊断方法

本文所用的资料为美国UMD（University of Maryland）的Carton（beta 7）逐月全球海洋同化分析资料[13]，对海洋上层，其可靠性较好，有关这方面的具体分析参见文献13和14。该资料已在国内外得到广泛应用[3-5，15-16]。本文所用的该资料提供了海洋上层1950—2001年共52年在深度112.5、97.5、82.5、67.5、52.5、37.5、22.5、7.5 m上的各月平均洋流，其水平方向采用高斯网格，网格距约为1°×1°。本文的统计动力诊断范围则取热带太平洋范围，其为30°S —30°N，120°E —180°E —80°W。这里采用的诊断方法为复EOF分析，其原理可参见文献2和17。具体操作步骤是：首先将各年各月份在上述8个深度上的各月平均流场分别求其52年的平均流场，将各年各月的平均流场减去该52年的平均流场，则可得各年各月这8层上的流场异常，即偏差流场；然后将各月这8层上的流场异常作为一个整体进行复EOF分析。此时各月各EOF模态的空间场和时间系数都是复数；各月空间场的模表示各月各模态流场异常的流速大小，辐角则表示其流向；而时间系数则表示这52年中各月流速、流向随年份的变化。由于这里将各月各层上的偏差流场看作一个整体来做复EOF分析，故各月各层有相同的时间系数，这也是该复EOF分析方法的特色和优点。本文主要讨论深度为7.5 m和112.5 m的两层，前者可作为表层的代表，后者可作为次表层的代表，为简单下文中就直接称呼这两层为表层和次表层。

3 诊断结果分析

该复EOF分析的结果表明，所得到的偏差流场前3个模态都通过了显著性检验[18]，各月第一、二模态的方差贡献见表1。由该表可见，第一模态方差贡献平均为30.5%，是最重要的模态，第二模态方差贡献平均为11.6%，其仍较重要，第三模态方差贡献平均为7.9%，相对较小。前3个模态累积方差贡献为50.0%，占总方差贡献的一半。从前三个模态方差贡献的月变化看，第一模态在冬季的方差贡献最大，春季次之，秋季最小；第二模态在秋季最大，春季次之，冬季最小；第三模态在秋季最大，夏季次之，冬季最小。由上分析可知，同一模态的大洋环流异常，其在各季节的重要性是各不相同的。因第三模态方差贡献较小，以下仅给出各季节第一、二模态的结果并进行讨论。

表1 热带太平洋各月各模态的方差贡献及其累计方差贡献

3.1 第一模态

表层1、4、7、10月份的空间场分布见图1，这4个月份在一定程度上可分别代表冬、春、夏和秋季，以下简称冬、春、夏、秋季。由图1可见，明显的流场异常均位于5°S—5°N之间，即其为赤道所俘获，并具有赤道陷波的性质。表层流场异常除在临近大洋东、西边界的小范围海域外，在整个太平洋的赤道上及临近赤道处，均表现为同一方向的纬向流，而几乎无经向流；在1、4、7月份更是如此，10月份则经向流稍大，但相比纬向流仍小很多。次表层则流场异常的分布与表层类似，并具有与表层相近的特点；在这8层上，该空间场的差异不大，这表明第一模态流场异常大体具有正压性。正因如此，在此略去了次表层的图。

从各月第一模态流场异常时间系数的辐角图（1、4、7、10月份见图2，其余图略）可见，一部分月份辐角大体集中在0°和 ± 180°附近（其中1、4、7、10月份均如此）。这表明此时辐角的分布有两个状态，可分别称其为态A、B。前者因辐角余弦值约为＋1，故其偏差流场的分布形势与该模态的空间场相同，而后者为-1，故该分布形势则与该空间场相反。另一部分月份的辐角大体集中在角α和180°+α附近，而角α则小于等于30°。这表明此时辐角的分布也有两个状态A、B。对这部分月份而言，相应于状态A，其流场异常的分布则需对原空间场的流向再做角度α的旋转；相对状态B，则要做180°+α的旋转；不过因这里角度α并不算太大（α≤30°），故在旋转后，态A、B仍保持与原空间场大致相同和相反的形势。综上，在此可分别称态A、B为相似态和相反态，因这时的偏差流场与该模态的空间场呈（大致）相同或相反的分布。由此可知，在1、7、10月份，当时间系数的辐角位于0°附近时，除在临近大洋东、西边界的小范围海域外，在整个太平洋上的赤道及临近赤道处，流场异常均为一致的西向流，而4月份则为一致的东向流；而当该辐角位于±180°附近时，则有流动的反向。其他各层次（含次表层）的情况则与表层类似。

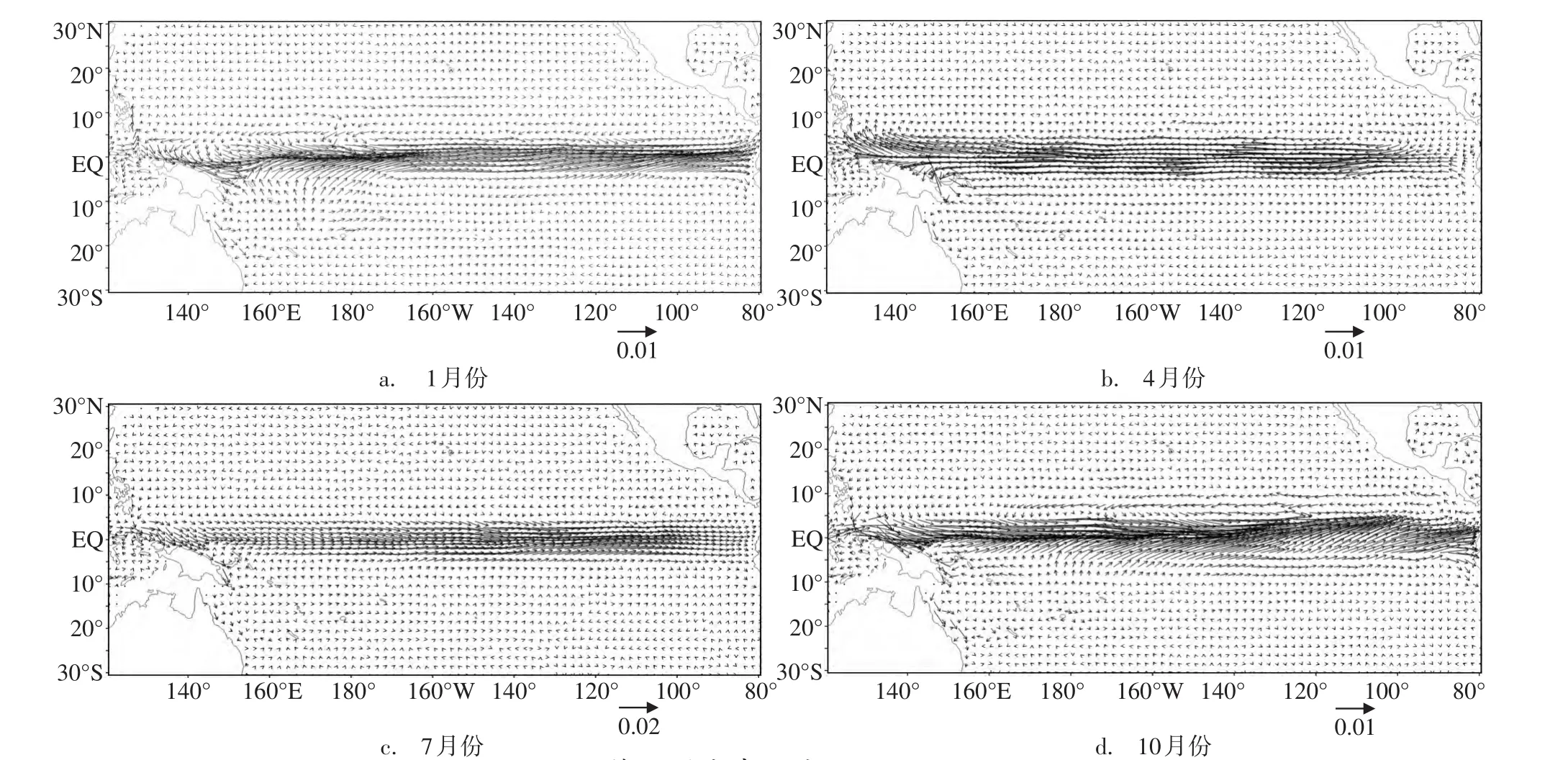
图1 第一模态表层空间场（单位/（m/s））

图2 第一模态时间系数的辐角(横坐标代表年份，纵坐标代表角度）

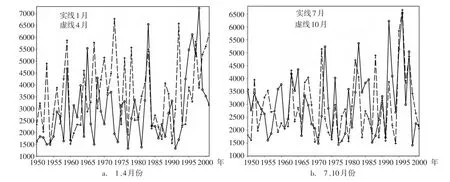
图3 第一模态时间系数的模

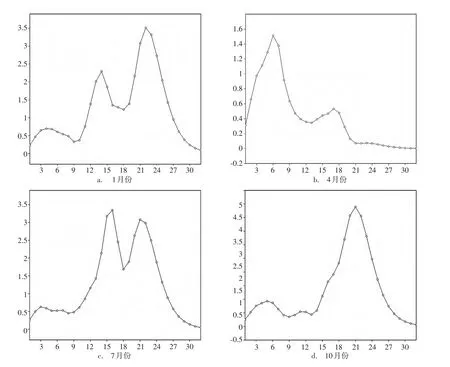
图4 第一模态时间系数序列的小波全谱

从各月第一模态流场异常时间系数模的图上（1、4、7、10月份参见图3，其余月份图略）可见，各月份该模的值每年也各不相同，为此求取各月模值的52年平均值。各月以该平均值为界，也可将其划分为两个态：大于等于该平均值的称为强模态S；小于该平均值的称为弱模态W；而各年模的数值大小则决定了其流场异常强弱的程度，数值越大则该流场异常就越大。

根据各月第一模态时间系数模和辐角的分类，可得以下4种配置组合：AS、BS、AW、BW，即相似强模、相反强模、相似弱模、相反弱模，这里相似与相反均对第一模态空间场而言。在此AS和BS是两个强异常的态，对于AS态则上述流场异常很强，而对BS态则流场异常的流动方向发生反向且强度也很强。

由第一模态流场异常时间系数辐角和模的演变可见（见图2—3），其具有明显的年际和年代际变化。为揭示四季时间系数的变化规律，因1、4、7、10月份辐角大体集中在0°和±180°附近，故可将这4个时间系数的模乘以其辐角的余弦值后构成一个新的实数时间序列（此时该余弦值约为±1，该新的实数时间序列的图略），该实数序列可综合反映辐角和模的时间演变，且便于分析。现对该序列作小波分析，图4给出了1、4、7、10月份即冬、春、夏、秋季该序列的小波全谱。由图4可见，四季均有3—7年的年际变化周期和十分明显的年代际变化周期；除春季外，年代际变化显著程度均远大于年际变化。在明显的年代际变化上；冬季有约14、22年的周期，且后者更显著；春季约有17年的周期，不过6年的年际变化更要显著，这是因此季节ENSO最明显的缘故；而夏秋两季则均有约21年的周期，在秋季则还有约16年的周期。综上，热带太平洋流场异常第一模态，其四季年际变化周期均在3—7年内，且在春季有最明显的约6年的周期；在其他季节则以21—22年的年代际变化周期表现最显著。

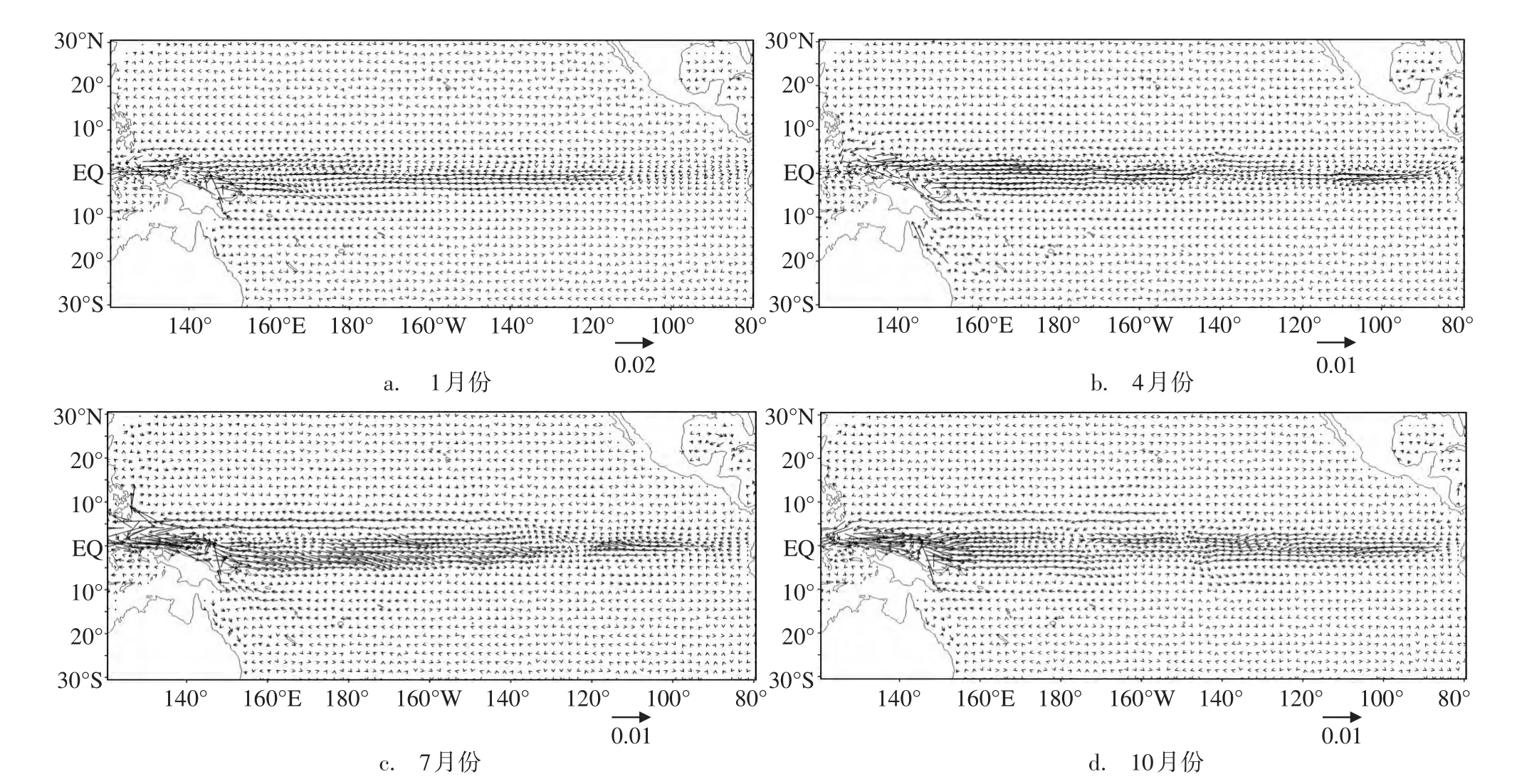
图5 第二模态次表层空间场（单位/(m/s））

3.2 第二模态

从诊断得到的第二模态各月空间场的分布可知，该模态的流场异常（偏差流动）仍为赤道所俘获，其也具有赤道陷波的性质。此时在海洋上层，赤道太平洋第二模态的流场异常则与第一模态不同；在邻近赤道的南北两侧，其纬向流异常的流动方向相反；在东、西太平洋的赤道上，纬向流异常的方向也不一致，并在某些地方还出现了经向流大于纬向流的情况。在赤道中太平洋海域，从表层以下直至次表层，纬向流流向大致关于赤道呈反对称分布形式，即在赤道北侧和南侧纬向流的流动方向相反，参见图5；该图分别给出了四季第二模态空间场在次表层上的结构。在表层以下直至次表层，第二模态空间场分布的差异也不大，即在海洋上层第二模态的流场异常仍具有正压性。

第二模态时间系数的辐角也有两个状态A、B，其与第一模态类似，但第二模态在以上A、B两个状态的离散度要较第一模态大（图略）。可仿照第一模态的做法，将第二模态模的值（其图略）也划分为强模态S和弱模态W；这样也能得到类似第一模态的4种配置态：AS、BS、AW、BW；其意义则与第一模态相同，不再赘述。

因四季（1、4、7、10月份）第二模态辐角的分布与相应的第一模态相同，均分布在0°和±180°附近，故可仿照第一模态的做法，对第二模态亦可得到综合反映辐角和模随时间变化的实数时间系数序列。该第二模态实数时间系数也具有明显的年际和年代际变化（图略）。

采用与第一模态同样的处理方法，对该实数时间系数序列做了小波分析（见图6）。结果表明，四季第二模态年代际变化周期均比年际变化周期要显著，而年际变化周期则均在3—7年内。年代际变化周期在冬季为12—13年、约18年和约24年，且以约18年的最显著；在春季为约15年和19—21年，且以19—21年的最显著；在夏季为约12年、约17年和约24年，且以约17年的最显著；在秋季为约17年和约24年，且以约17年的最显著。综上，四季第二模态的年际变化周期均在3—7年内，而最明显的年代际变化周期均在18年左右，此外冬、夏、秋还有约24年的周期，春季该周期缩短为19—21年。

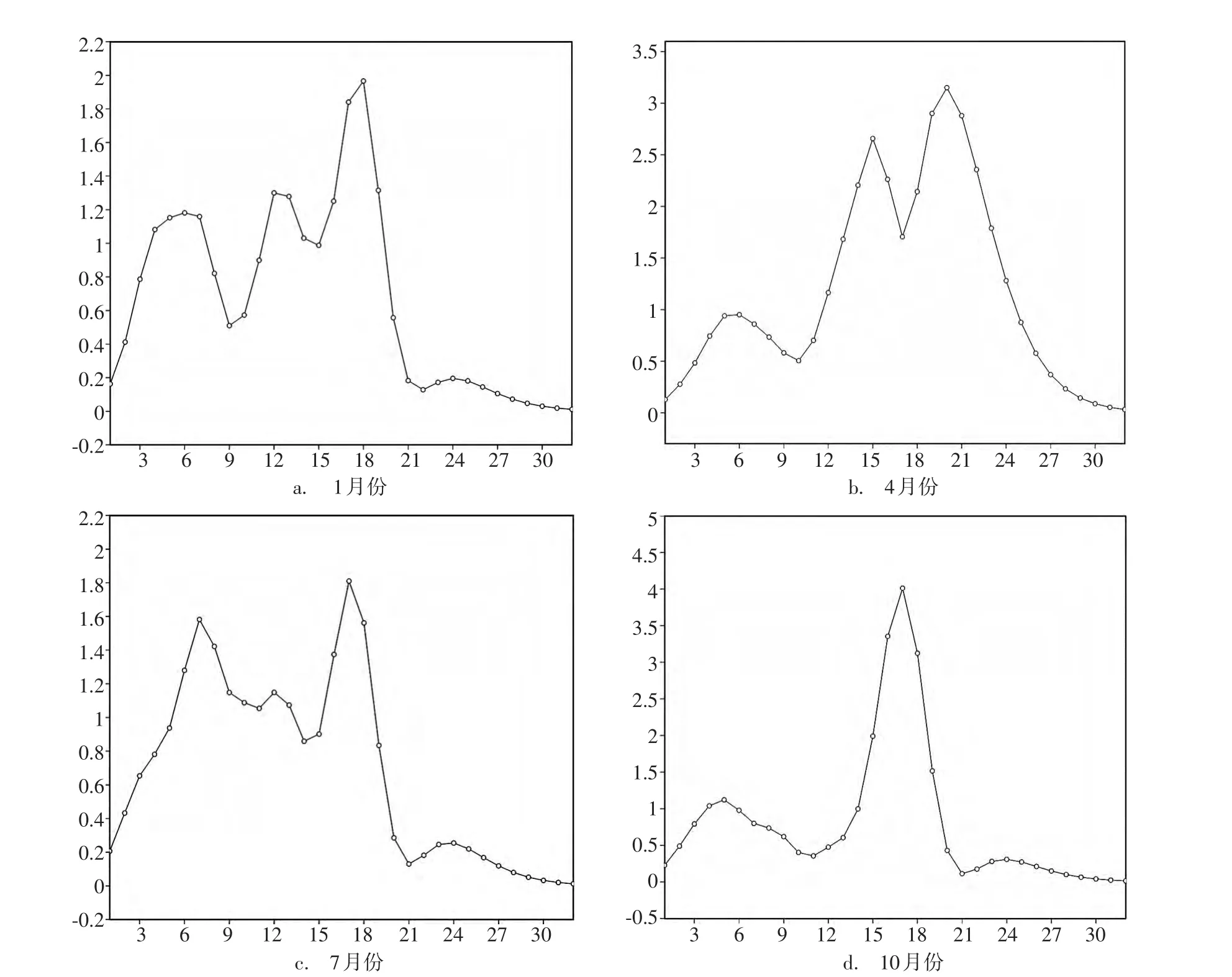
图6 第二模态时间系数序列的小波全谱

4 各模态的特点性质

4.1 第一模态

由第一模态空间场的性质知，其具有赤道海洋Kelvin波的特点；该特点为，其流场的纬向流的最大值出现在赤道，且关于赤道呈对称分布，并随纬度的增高其呈指数迅速衰减，而经向流则几乎为0；故而该第一模态的性质为赤道海洋Kelvin波的异常。

海洋次表层的垂直运动异常与海温的动力异常有着密切的关系，当该层某处垂直运动为正，即有上升流时，则会造成该处的动力降温；反之亦然。由本文的复EOF分析得到的各模态流场异常可直接计算其各层的散度场异常，对该散度场异常在垂直方向积分则可算得相应的垂直速度异常（计算时取海气界面处的海洋垂直运动w≈0）；这样w＞0（w＜0）则对应于上升（下沉）运动异常[15]；而由近表层（在此为22.5 m处）的垂直速度异常则可方便地决定SST异常的动力变化。

图7给出了该第一模态由各季近表层（22.5 m处）流场异常计算得到的相应垂直运动的异常。由该图可见：1月份，在赤道西太平洋至赤道中太平洋上垂直运动有下沉带，而赤道中太平洋到秘鲁沿岸则有上升带(见图7a)；这表明，前者处SST的动力异常为暖异常，后者处为冷异常。4月份垂直运动异常和SST动力异常的分布则与1月份大致相反，即原下沉运动处现为上升运动，暖异常处现为冷异常(见图7b)，注意，此时空间场的流动异常也大致相反。7、10月份，因流动异常与1月份类似，故垂直运动异常(见图7c、d)和SST动力异常的分布也与1月份类似。

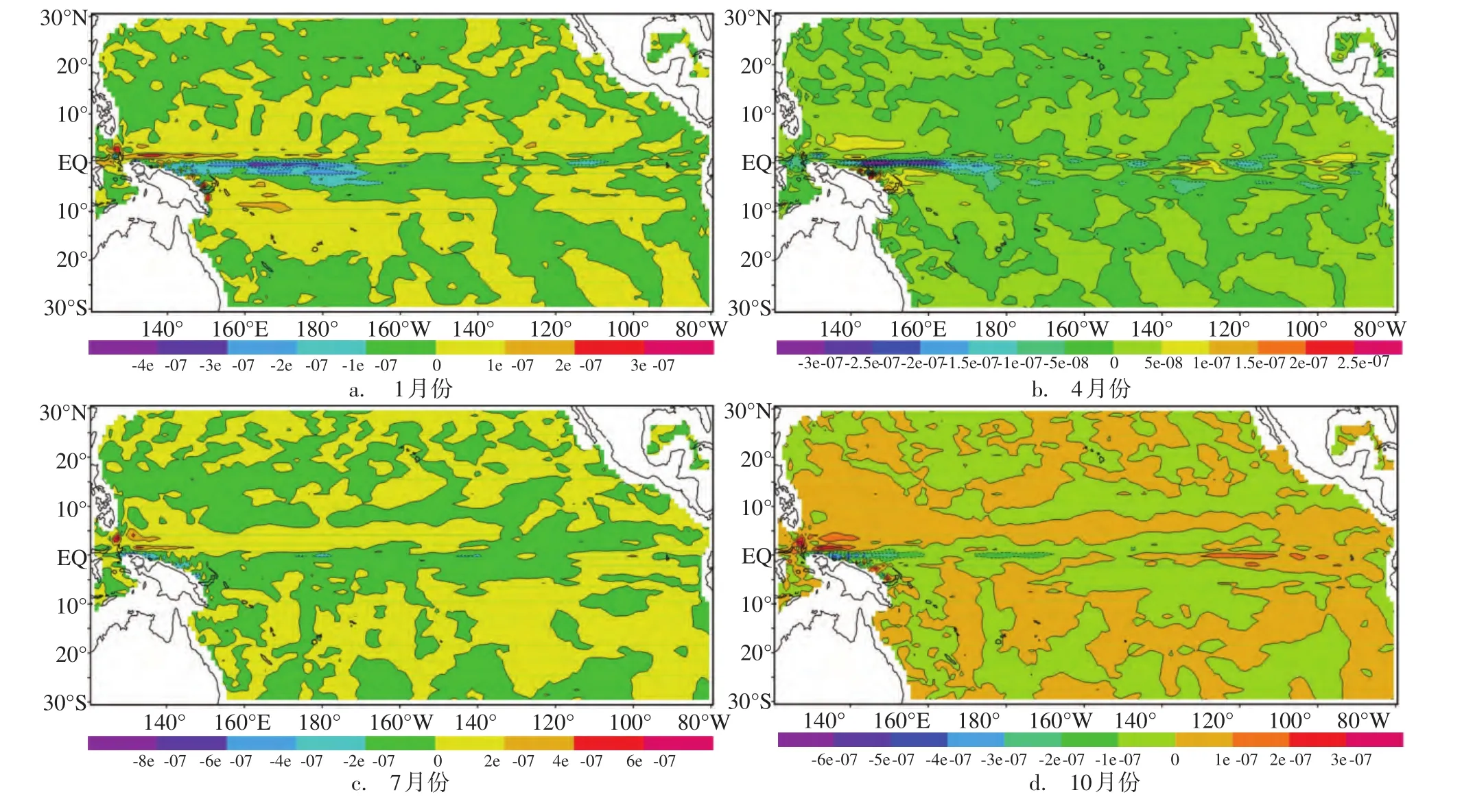
图8 第二模态垂直运动场分布（单位/kg ms2）

以上是该模态时间系数为正时的情况，当该系数为负时，则SST的动力异常发生反相，偏高转为偏低，反之亦然。这样当时间系数作3—7年（年际）正负间的交替变化时，赤道上的SST动力异常则在西太平洋和东太平洋作相应东西向的跷跷板式变化。而这与ENSO主要的SSTA变化一致。为此可称第一模态为ENSO的主要模态，并可见ENSO与Kelvin波的异常关系很密切。

4.2 第二模态

海洋混合Rossby-重力惯性波也是一种重要的赤道陷波，经典的该混合波的特点为：波动关于赤道呈反对称分布，在赤道两侧流向相反，其最大振幅也出现在该处；在赤道上有最大的经向流。在东、西边界海域之外，由第二模态的空间场知（见图5），其分布与上述经典的该混合波大体类似。经典的该波是无背景流（基本流）的，而该第二模态空间场则由实际海洋资料诊断而得，应包含背景流等其他因素的影响，故两者有一定差异也是正常的；不过从总体上来看，在第二模态空间场上该经典混合波的特点还是表现明显的；这样第二模态的性质应为海洋混合Rossby-重力惯性波的异常。

图8给出了该第二模态由各季近表层（22.5 m处）流场异常计算得到的相应垂直运动的异常，以便据此来推断SST的动力异常。由该图可见：各季从西太平洋到中太平洋垂直运动异常在赤道上及其临近处均有下沉带，在该下沉带两侧则有上升带；在西太平洋该下沉带上垂直运动异常很强，但各季的强度表现并不一样，在该下沉带北面的西太平洋暖池海域，则为较强的上升区，各季则该上升区的强度表现也并不相同。

由赤道太平洋海域近表层的垂直速度异常可推断出SST的动力异常。该动力异常表现为，各季从西太平洋到中太平洋在赤道上和临近赤道处，其均表现为一条偏高带，在该偏高带的南北两侧则为偏低带；在西太平洋，该偏高带上的异常很强，而在该该偏高带北侧的西太平洋暖池海域则有有较强的偏低区；各季在这些偏高、低带和偏低区，其动力异常的强度也不一样。以上是时间系数为正时的情况。当时间系数为负时，该SST动力异常则也反相。这样当时间系数在3—7年（年际）内做正负间摆动时，在西太平洋赤道上以及其北的该暖池海域，SST动力异常则有南北向跷跷板式的变化，而这正与ENSO在该两处特别是在该暖池海域上的SS⁃TA变化一致。然而因ENSO在赤道上SSTA的东西向变化要较南北向变化更重要和显著，两者相比后者则相对处于次要地位。这样可称该第二模态为ENSO的次要模态。由此还可见，ENSO与混合Rossby-重力惯性波异常的关系也很密切。

4.3 有关年代际变化的讨论

上面已指出，从年际变化出发，本文复EOF分解的第一、二模态可分别看作ENSO的主要、次要模态。然而这两模态还都有明显的年代际变化，通常其比年际变化还要显著。冬季，第一模态分别有约22年、14年的年代际变化周期，且前者表现更显著；第二模态则有约24年、约18年和12—13年的该周期，且以18年的表现最显著。在注意到冬季这两个模态的年代际变化周期与引言中冬季PDO、NPGO的该周期（分别为约22年和约13年），以及冬季热带外北太平洋流场异常复EOF分解[5]的第一、二模态的该周期（分别为约20年和约18年、约14年）相同或相近之后（这里只给出了冬季的情况，其他季节因缺乏相应研究故未讨论）；可知此情况的出现决不是偶然的，而是引言中所述的热带与中纬度各大气、海洋系统之间相互耦合的结果，并值得深入研究。

5 结语

本文采用复EOF分析方法，对全年热带太平洋海域的上层洋流异常做了统计动力诊断，得到了以下主要结论：

（1）热带太平洋上层洋流异常复EOF分解第一、二模态的空间场均为赤道所俘获，并均在南北方向呈迅速衰减的态势，其表现为赤道陷波的形式；

（2）第一、二模态时间系数为复数，其辐角均集中在两个状态，其模则表示了流场异常的大小；为此可用一个实时间序列序列来表示该系数，从而使问题得到简化；

（3）该时间系数都有年际和年代际变化；前者的周期均与ENSO相同，在冬季，后者的周期与PDO和NPGO，以及热带外北太平洋流场异常复EOF分解前两模态的周期相同或相近，这反映了热带与中纬度各大气、海洋系统之间的相互耦合；

（4）由各模态流场异常可得相应的垂直运动异常，从而可估计SSTA的动力变化；第一模态的变化在赤道东、西太平洋处呈现东西向的跷跷板变化；第二模态的变化则在西太平洋的赤道上以及其北侧的西太平洋暖池处，呈现南北向的跷跷板变化；

（5）第一模态的性质为海洋赤道Kelvin波的异常，可称之为ENSO的主要模态；第二模态的性质为海洋混合Rossby-重力惯性波的异常，可称之为EN⁃SO的次要模态。

最后要指出的是，本文主要工作是进行诊断分析，对造成热带太平洋大洋环流异常的原因分析得尚不够；另外，本文也未研究热带太平洋大洋环流异常对我国天气气候的影响，这些都是我们今后所要进行的工作。

［1］蔡怡.赤道太平洋温度、流场距平EOF分析及与厄尔尼诺的关系[J].海洋学报,2003,25(1):12-18.

［2］黄嘉佑.气象统计分析与预报方法[M].北京:气象出版社,2000:135-139.

［3］卢姁,张东凌.10月份热带印度洋海气耦合的统计动力诊断[J].大气科学,2010,34(2):351-360.

［4］卢姁,张东凌.热带太平洋5月份上层洋流的动力统计诊断[J].热带海洋学报,2009,28(2):22-30.

［5］吕庆平,卢姁,张铭.冬季赤道外北太平洋流场异常的复EOF诊断分析[C].第28届中国气象学会年会,福建厦门,2011.

［6］杨修群,朱益民,谢倩,等.太平洋年代际振荡的研究进展[J].大气科学,2004,28(6):79-992.

［7］张立凤,吕庆平,张永垂.北太平洋涡旋振荡的研究进展[J].地球科学进展,2011,26(11):1143-1149.

［8］Di Lorenzo E,Schneider N,Cobb K M,et al.ENSO and the North Pacific Gyre Oscillation:an integrated view of Pacific decadal dynamics[J].Geophysical Research Letters,2009(Submitted).

［9］Vimont D J,Wallace J M,Battisti D S.The seasonal footprintingmechanism in the Pacific:Implications for ENSO[J].Journal of Climate,2003,16(16):2668-2675.

［10］Anderson B T.Tropical Pacific sea-surface temperatures and preceding sea level pressure anomalies in the subtropical North Pacific[J].Journal of Geophysical Research-Atmospheres,2003,108(D23):18.

［11］Yu J Y,Kao H Y,Lee T.Subtropics-related interannual sea surface temperature variability in the equatorial central Pacific[J].Journal of Climate,2010,23(11):2869-2884.

［12］Yu J Y,Kim S T.Relationships between extratropical sea level pressure variations and the central-Pacific and eastern-Pacific types of ENSO[J].Journal of Climate,2011,24(3):708-720.

［13］Carton JA,Chepurin G,Cao X,et al.ASimple Ocean Data Assimilation analysis of the global upper ocean 1950-1995,Part I[J].J Phys Oceanogr,2000,30(2):294-309.

［14］Carton,J A,Chepurin G,Cao X.A Simple Ocean Data Assimilation analysis of the global upper ocean 1950-1995 Part 2:Results[J].J Phys Oceanogr,2000b:30:311-326.

［15］张东凌,曾庆存.5月热带印度洋大气大洋耦合环流的统计动力分析[J].中国科学D辑,2007,37(12):1693-1699.

［16］Carton J A,Hackert E C.Data assimilation applied to the temperature and circulation in the tropical Atlantic1983-84[J].J Phys Oceanogr,1990,20:1150-1165.

［17］曾庆存.大气红外遥感原理[M].北京:科学出版社,1974:160-166.

［18］North G R,Bell T L,Cahalan R F,et al.Sampling errors in the estimation of empirical orthogonal function.Mon Wea Rev,1982(110):699-706.