热带气旋风场非对称性对表面海浪场的影响

洪新，赵玮，候查伟

（1.国家海洋局烟台海洋环境监测中心站，山东烟台 264006；2.中国海洋大学，山东青岛 266100）

1 引言

热带气旋是热带或副热带海区最为严重的自然灾害，其带来的狂风、巨浪、暴雨和风暴潮等恶劣海洋天气现象每年都对我国海上石油平台、远洋运输以及沿海地区经济和人民生命财产的安全造成严重威胁和巨大损失，准确预报热带气旋的强度、结构及热带气旋产生的海浪对减灾具有重大意义。由于热带气旋下海浪场的空间分布特征主要依赖于热带气旋风场，因此了解风场的细结构如何影响海浪场是十分必要地。

过去几十年，通过观测研究和数值模拟的方法做了大量努力来研究热带气旋下海浪场对风的响应。通过数据分析已经证实了热带气旋移动速度，最大风速，最大风速半径以及先前生成的并随着气旋移动的涌浪是海浪平均要素空间分布特征的最主要影响因素[1-7]。Wright等[8]和 Walsh 等[9]用 NASA机载扫描雷达高度计数据首次研究了热带气旋Bonnie在开阔大洋和登陆情况下各象限的海浪方向谱的空间分布特征。Young[10]用全面的方向海浪浮标数据提供了在热带气旋通过时的海浪方向谱。另一方面，海浪模式也被用来研究热带气旋下的海浪场而没有观测的限制，并且海浪模式的模拟结果已经被证实了与实际观测结果符合的很好，可以被用来研究热带气旋下海浪场的特征及其影响因素[11-18]。Moon 等[11]用WAVEWATCHIII（WW3）模式模拟了热带气旋Bonnie下的海浪方向谱，与实际观测符合的很好且进一步研究了热带气旋移动速度对方向谱的影响。其他一些研究用WW3或SWAN模式探讨了热带气旋强度，风场分布，背景风场，最大风速半径，与气旋中心相对距离以及入流角度对海浪平均要素和方向谱的影响[13-14,19-20]。然而，海浪场对热带气旋风场非对称性的响应却并没有受到关注，而已有研究发现非对称风场和对称风场下海浪的空间分布特征是不同的[20-21]。

在Zhao and Hong文章中[21]，我们用WW3海浪模式研究了热带气旋入流角度对海浪场的影响。在这个研究中我们用同样的方法致力于探讨热带气旋风场非对称性对海浪场的影响。为了这个目的，我们选了五个具有不同非对称性风场的理想热带气旋做敏感性实验，并将结果作对比。第二部分中会介绍WW3海浪模式。第三部分我们介绍了敏感性实验设计方案和风场的计算方法。第四部分讨论热带气旋风场非对称性对海浪场的影响。第五部分给出结论。

2 WAVEWATCHIII海浪模式介绍及设置

WAVEWATCHIII（WW3）模式是由NOAA/NCEP开发的高分辨率表面海浪模式。它是继Delft University of Technology研发的WAVEWATCHI和NASA Goddard Space Flight Center研发的WAVE⁃WATCHII之后的第三代海浪模式。WW3海浪模式中的源函数包括风-浪相互作用项Sin，波-波相互作用项Snl，白冠耗散Sds，在浅水中还要考虑底摩擦耗散项Sbot。它在假设介质（深度和海流）和海浪场在时间和空间尺度上的变化比单个波变化尺度要大得多的情况下，解决了方向波数谱的谱密度平衡方程。但是模式不包括海浪受深度限制的情况，这就意味着WW3模式可以应用在空间尺度超过1—10km并且在海浪破碎带之外的海域。这个海浪模式可以输出网格区域的海浪方向谱以及有效波高（）、平均波长（）、平均波周期（）、平均波向、峰频、峰向等平均海浪要素。其中，E是谱能量，k是波数，σ是角频率。峰频是通过对一维频谱的离散峰值进行抛物线拟合计算获得的。峰的波数（波长）是利用频散关系和峰频计算获得的。

本研究中WW3模式的模拟空间范围为经向2000 km，纬向3500 km，平均水深5000 m,空间分辨率为9 km×9 km，谱分辨率为48个方向（7.5°），25个频率（从0.0418到0.41），风能输入时间间隔为600 s，海浪要素平均参数输出时间步长为3600 s。

3 实验设计

我们设计实验来研究热带气旋应力下风场非对称性对海浪场的影响。实验中选取三级理想热带气旋（根据Saffir-Simpson分级方法）的风场作为模式的输入风场，其包括Willoughby理想风剖面，移动速度和SLOSH入流角度三个部分。其中，Wil⁃loughby理想风剖面是通过一个热带气旋风场统计参数模型计算获得的随半径变化的轴对称切向风[22-23]，SLOSH入流角度是由美国NOAA的SLOSH技术报告中基于大量观测数据建立的入流角度统计模型计算获得[24]。在此基础上，通过一个因数来改变热带气旋风场的非对称性，它可以表述为：U=U0× [a-(1-a)× cosӨw]。其中，U代表非对称风场风速，U0是对称风场风速，a是非对称因子，Өw是风向。

在这个研究中我们用了5个理想热带气旋来探讨风场非对称性对表面海浪场的影响（见表1）。在这些实验中，最大风速和最大风速半径分别为56 m/s和50 km。假设热带气旋以5 m/s的速度在深度为5000 m，范围为经向3500 km，纬向2000 km的矩形大洋上匀速直线移动（见图1）。图1中矢量代表风的大小（m/s）和方向，空心长箭头代表热带气旋移动方向，等值线代表等风速线，单位为m/s。风场的最大风速为56 m/s，最大风速半径为50 km，入流角度为SLOSH报告中入流角度统计模型计算获得的随半径变化的值。风场的时间分辨率为600 s，空间分辨率为9 km×9 km。

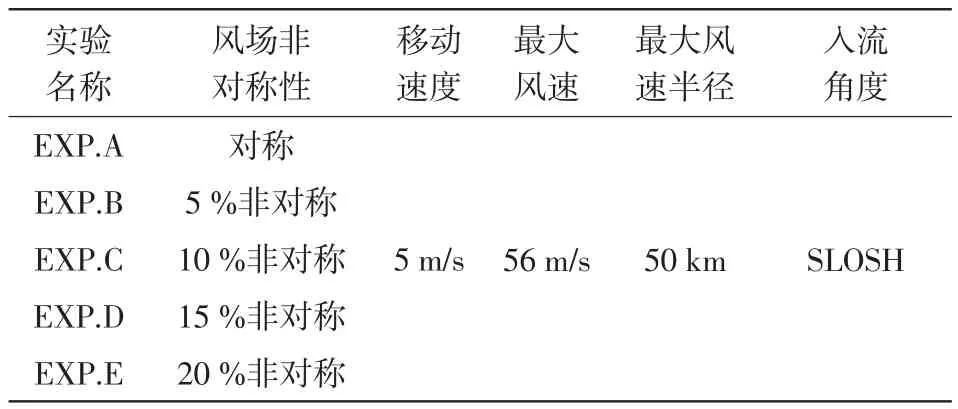
表1 实验设计方案

图1 WW3海浪模式的模拟区域以及理想热带气旋风场分布图

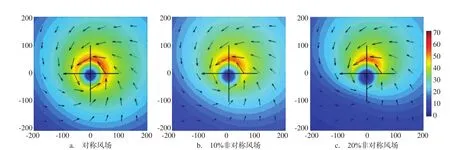
图2 热带气旋风场的空间分布特征随非对称性增强的变化

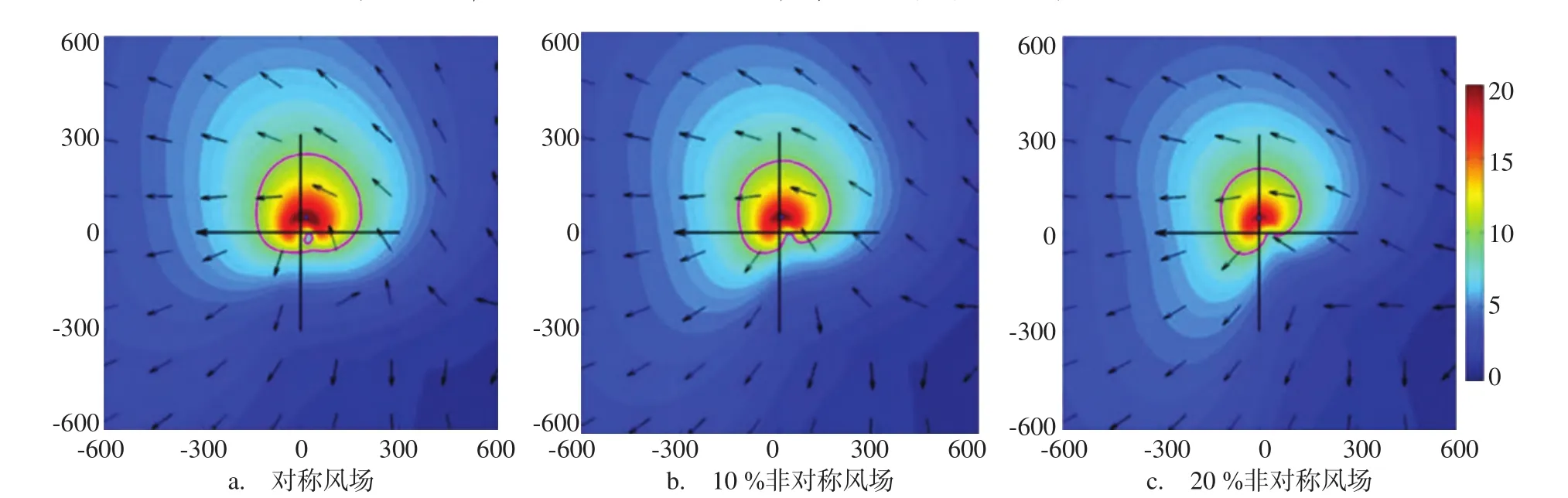
图3 有效波高（颜色，单位/m）和平均波向（矢量）的空间分布特征随热带气旋非对称性增强的变化

模式共运行72 h，由于模式积分所利用的理想风场，热带气旋中心以恒定速度自东向西移动，而其风速大小相对于气旋中心是恒定的，则模式计算区域内海浪平均要素随时间发展将会逐渐趋于稳定。实验中有效波高在24 h后可以达到稳定状态，在下面的讨论中我们只对第72 h的数据进行分析。由于一个热带气旋会产生复杂的并且空间上快速变化的海浪谱，我们模拟了第72 h所有网格点上的海浪谱。在分析海浪方向谱时，我们分别选取了4个象限内距气旋中心100 km半径上的8个点为代表进行对比研究。通过风场空间分布特征的对比显示随着风场非对称性加强风速减小,并且左侧象限减小的比右侧象限更快（见图2）。

4 热带气旋风场非对称性对海浪场的影响

4.1 对有效波高的影响

通过对比可以看出，最大有效波高值会随着风场非对称性加强而减小。在EXP.A中，最大有效波高为22 m，当对称性增加到20%时最大有效波高减小到20 m，减小了9%。1000 km半径内的平均有效波高随着非对称性增强除了左前象限以外，其他象限内由于风应力的减小而减小。实验EXP.E和EXP.A之间的对比显示，平均有效波高分别在右前象限、右后象限、左后象限减小了9.26%，20.16%，19.52%，在左前象限增大了13.01%。

图3展示了不同热带气旋风场下有效波高的空间分布。从图中可以清楚地看到热带气旋风场的非对称分布对海浪场的空间非对称性有重要的影响，风场分布越不对称，有效波高场分布越不对称。同时，有效波高场的非对称轴随着风场非称性加强逆时针旋转，最大有效波高的位置向前移动。实验EXP.E与EXP.A相比看出，有效波高场的空间非对称轴由气旋移动方向右偏80°逆时针移动到右偏50°，逆时针旋转了30°，与风场逆时针旋转的角度相同，最大有效波高的位置由右后象限移动到右前象限，这与以往的实际观测结果一致。这是因为随着风场非对称性加强，风速减小，风能输入减少，根据海浪能量平衡方程可知，风能输入源函数项Sin减小，则波浪能量E减小，而波浪有效波高与波能量E的平方根成正比减小，因此有效波高随风场非对称性加强而减小，最大有效波高减小。在左前象限，虽然风力减小使局地风浪能量减少，却更有利于先前位置生成的涌浪的传播，涌浪部分能量增加，因此总体能量增加，有效波高增高。

4.2 对平均波向的影响

不同实验之间平均波向的空间分布的对比表明热带气旋风场的非对称性会影响平均波向，尤其是在左后象限最为显著（见图3）。在右前和左前两个象限，风场非对称平均波向基本没有影响，除了在左前象限距离风暴中心前100 km，左300 km的长方形区域内平均波向随非对称性加强发生顺时针旋转，当非对称性增加到20%时，平均波向旋转了10°—60°。这是由于在前两个象限内主导波为远处生成的涌浪，平均波向主要由涌浪的传播方向来决定，而这两个象限中涌浪的传播方向主要与热带气旋移动的方向有关，因此，在这两个象限内大多数区域波向没有变化。在那个特殊区域，主导波包含了风浪和涌浪，随风速减小，主导波中的风浪消失，平均波向会向着涌浪的传播方向旋转。

在左后和右后两个象限内，平均波向随着非对称性增强而发生逆时针旋转。当非对称性达到20%时，在右后象限旋转了10°—30°，而在左后象限旋转的角度甚至超过了180°。在左后象限，主导波包含了风浪和涌浪。随着非对称性增强，由于风应力的减小，风浪部分减弱，涌浪的影响增强。因此，平均波向会向着涌浪的传播方向旋转。在左后象限的某些区域，当非对称性达到15%时，主导波中的风浪消失，只剩下涌浪。

4.3 对平均波长和平均周期的影响

图4 平均波长（颜色，单位/m）和峰向（矢量）的空间分布特征随风场非对称性增强的变化

图5 平均周期（单位/s）的空间分布特征随风场非对称性增强的变化

图6 左前象限的海浪方向谱分布特征随热带气旋风场非对称性增强的对比

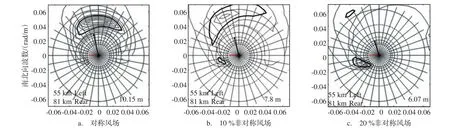
图7 左后象限的海浪方向谱分布特征随着热带气旋风场非对称性增强的对比

从图4可以看出，除了在正左侧和左后象限外，随着风场非对称性增强平均波长减小。当风场非对称性达到20%时，平均波长在右前象限，右后象限和左前象限分别减小了10—40 m，30—70 m，10—50 m。在热带气旋中心正左侧增加了0—140 m，在左后象限，平均波长在400 km半径内从气旋中心向外增加100—0 m，在这之外的范围减小了0—40 m。平均波长随着非对称性增强的这种变化可以解释为风浪部分的波长随着风速的减小而变短，因此大部分区域波长是减小的，然而，在气旋中心左侧和左后象限，随着风力的减小，主导波中风浪部分消失，较长的低频涌浪为主导波，因此，在这些范围内平均波长增大。

另外，随着热带气旋风场非对称性的增强，风力减小，海浪场能量E减小，由于平均波长与波能量E成正比，因此平均周期在各个象限内略有减小。当非对称性达到20%时，各个象限的平均周期均减小了2—3 s左右（见图5）。

4.4 对波峰方向的影响

热带气旋风场的非对称性对波峰方向也有影响（见图4中矢量方向）。随着非对称性加强，峰向在前两个象限没有变化，在后两个象限逆时针旋转。当非对称性增强到20%时，右后象限旋转了10°—60°，在左后象限旋转达到了180°。这种现象的解释与平均波向相同。

4.5 对海浪方向谱的影响

在这个研究中，我们选了第72 h距热带气旋中心100 km半径上的5个点来对研究风场非对称性对海浪方向谱的影响（见图6—7，以左前象限和左后象限为例）。图中实线等值线（从外向内）代表100 m，200 m，300 m，400 m波长。虚线等值线（从外向内）代表150 m，250 m，350 m波长。每个谱包含五个等值线，分别为谱峰密度的10%—90%，增长率为20%，加粗的等值线代表谱峰密度的50%。左下角信息表示模拟点距热带气旋中心的距离。加粗的黑色箭头代表风速，0.03 rad/m的长度相当于30 m/s的风速。右下角的数字代表有效波高，红色加粗箭头代表热带气旋的移动方向和移动速度大小。不同风场非对称性下方向谱的对比显示非对称性对海浪谱的多峰性有重要作用，对海浪谱的频率以及主导波的传播方向都有重要影响。

在右前象限，实验EXP.A中，主导波为波长较长的沿着热带气旋移动方向传播的涌浪且传播方向为30°。随着非对称性加强，方向谱的谱形没有明显变化，只是频率变高。在左前象限大部分区域，主导波为在气旋移动方向左偏20°—50°方向传播的涌浪，且随着风场非对称性增强没有明显变化。但是在气旋中心左侧，方向谱随着非对称性增强有显著地变化。在这里，主导波包含涌浪和风浪两部分，随着非对称性增强，风浪部分消失，主导波只包含涌浪，在非对称性达到15%之前，海浪谱仍然是双峰的。当非对称性达到15%之后，双峰结构消失，主导波沿着气旋移动方向左偏30°—60°方向传播。显而易见，在气旋前面的两个象限内，主导波为涌浪且海浪谱是单峰的，这与观测结果一致。在右后象限，主导波为局地生成的风浪。随着非对称性增强，局地风能量减小，风浪减弱，主导波的传播方向向着气旋移动方向逆时针旋转，而谱形基本没有变化。在左后象限，实验EXP.A中主导波为风浪。随着风场非对称性增强，涌浪逐渐增强成长为主导波，而风浪逐渐减弱，但是没有消失，海浪谱出现双峰结构，这与观测结果也很吻合。

5 结论

在这个研究中，我们用WW3模式研究了热带气旋风场的非对称性对表面海浪场的影响。模拟结果显示风场的非对称性对海浪平均要素和海浪方向谱都有很重要的影响。从非对称性分别为0%,5%,10%,15%和20%的五个理想热带气旋的模拟中，我们详细地讨论了非对称风场对表面海浪场的作用。

热带气旋下的海浪场包含远处传来的涌浪和局地生成的风浪两部分。随风场非对称性增强，由于风应力减小风浪减弱，有效波高在所有象限内减小，除了左前象限。波高场的非对称性增强且非对称轴逆时针旋转，最大有效波高位置向前移动，同时平均波长变短，平均周期变短。

在热带气旋中心前两个象限内主导波为先前位置生成的随着气旋移动的涌浪。因此，平均波向和波峰方向随风场非对称性增强基本没有变化。在右后象限，随着风场非对称性加强，平均波向和波峰方向会向着气旋移动方向逆时针旋转。在左后象限，随着风场非对称性增强，平均波长和峰向变化很大，甚至达到180°，并且波长在左后象限也变长。

热带气旋风场的非对称性会影响海浪谱的多峰结构以及主导波的频率和传播方向。但是风场非对称性对海浪谱的影响主要依赖于与气旋中心的相对位置。

[1]Elachi C,Thompson T W,King D B.Observations of the ocean wave pattern under Hurricane Gloria with synthetic aperture radar[J].Science,1977,198(4317):609-610.

[2]Gonzalez F I,Thompson T E,Brown W E,et al.Seasat wind and wave observations of Northeast Pacific Hurricane Iva,August 13,1978[J].Journal of Geophysical Research,1982,87(C5):3431-3438.

[3]Holt B,Gonzalez F I.SIR-B observations of dominant ocean waves near Hurricane Josephine[J].Journal of Geophysical Research,1986,91(C7):8595-8598.

[4]King D B,Shemdin O H.Radar observation of hurricane wave directions[J].Paper presented at 16th International Coastal Engineering Conference,Hamburg,Germany,ASCE,1978:209-226.

[5]McLeish W,Ross D B.Imaging radar observations of directional properties of ocean waves[J].Journal of Geophysical Research,1983,88(C7):4407-4419.

[6]Young I R,Burchell G P.Hurricane generated waves as observed by satellite[J].Ocean Engineering,1996,23(8):761-776.

[7]Young I R.A review of the sea state generated by Hurricanes[J].Marine Structures,2003,16(3):201-218.

[8]Walsh E J,Wright C W,Vandemark D,et al.Hurricane directional wave spectrum spatial variation at landfall[J].Journal of Physical Oceanography,2002,32(6):1667-1684.

[9]Wright C W,Walsh E J,Vandemark D,et al.Hurricane Directional Wave Spectrum Spatial Variation in the Open Ocean[J].Journal of Physical Oceanography,2001,31(8):2472-2488.

[10]Young I R.Directional spectra of hurricane wind waves[J].Journal of Geophysical Research,2006,111(C08020):doi:10.1029/2006JC003540.

[11]Moon I J,Walsh E J,Ginis I,et al.Numerical Simulation of Sea Surface Directional Wave Spectrum under Hurricane Wind Forcing[J].Journal of Geophysical Research,2003,33(8):1680-1706.

[12]Tolman H L,Alives J-H G M,Chao Y Y.Operational Forecasting of Wind-Generated Waves by Hurricane Isabel at NCEP[J].Weather and Forecasting,2005,20(4):544-557.

[13]Xu F M,Perrieb W,Zhang J,et al.Toulany Simulation of typhoon-driven waves in the Yangtze Estuary with multiple nested wave model[J].China Ocean Engineering,2005,19(4):613-624.

[14]Xu F M,Perrie W,Toulany B,et al.Wind-generation waves in hurricane Juan[J].Ocean Modeling,2007,16(3-4):188-205.

[15]陈希,闵锦忠.近岸海浪模式在中国东海台风浪模拟中的应用—数值模拟及物理过程研究[J].海洋通报,2003,22(2):9-16.

[16]丁亚梅,董克慧,周林,等.大气-海浪耦合模式对台风“碧利斯”的数值模拟[J].海洋预报,2009,26(2):15-26.

[17]蒋小平,钟中,张金善,等.台风Winnie（1997）影响下海浪的数值模拟研究[J].热带气象学报,2007,23(4):376-382.

[18]于卫东,乔方利,袁业立,等.Betty（8710）台风过程风、浪数值模拟[J].海洋学报,1997,19(6):27-37.

[19]Liu H Q,Xie L,Leonard J,et al.Sensitivity of wind waves to hurricane wind characteristics[J].Ocean Modelling,2007,18:37-52.

[20]Zhao W,Chen S S.Hurricane Forced Ocean Surface Waves and Potential Feedback[J].Investigation of Tropical and Extra-tropical cyclones using passive and active microwave radar(EXTROP),Miami,USA,2006.

[21]Zhao W,Hong X.Impacts of tropical cyclone inflow angle on ocean surface waves[J].Chinese Journal of Oceanology and Limnology,2011,29(2):460-469.

[22]Willoughby H E,Rahn M E.Parametric Representation of the Primary Hurricane Vortex.Part I:Observations and Evaluation of the Holland(1980)Model[J].Monthly Weather Review,2004,132(12):3033-3048.

[23]Willoughby H E,Darling R W R,Rahn M E.Parametric Representation of the Primary Hurricane Vortex.Part II:A New Family of Sectionally Continuous Profiles.Model[J].Monthly Weather Review,2005,134(4):1102-1120.

[24]Jelesnianski C P,Chen J,Shaffer W A.SLOSH:Sea,Lake,and Overland Surges from Hurricane[M].USA,NOAA Technical Report NWS 48,1992:4-23.