油水两相间界面张力系数对胶凝原油单颗粒运动状态影响的数值模拟研究

刘晓燕，赵辰辰，李晓庆，李友行，刘立君

（l. 东北石油大学防灾减灾及防护工程黑龙江省高校重点实验室， 黑龙江 大庆 163318;2. 东北石油大学土木建筑工程学院， 黑龙江 大庆 163318）

我国原油大部分具有高含蜡、高凝点和高粘度，即“三高”特点。在寒区油田，对高凝原油采出液实行低温集输与处理，一直是国内外油田节能降耗技术领域里的一大难题[1-3]。刘晓燕课题组在大庆油田现场进行不加热实验时，发现在特高含水原油集输管道中原油在某些低于凝固点的工况下会出现胶凝颗粒状态，悬浮在水中流动。现已通过实验，使胶凝原油呈现不规则的非连续相颗粒状态,悬浮在水中,在温度远低于凝点后仍能流态化输送[4]。

水胶凝原油两相流具有复杂的流变特性，当流体温度在原油凝固点附近时，油气集输过程中胶凝原油可以表现出固态(凝胶颗粒)、拟固态(此时，原油呈现软物质特性，与固态颗粒相比密度、硬度、强度等下降，呈现柔软特性)、拟流体(此时，液态原油中夹杂着固态颗粒，粘度、密度等大于液态)和液态(流体)4种状态。为掌胶凝原油颗粒的流动形态及流动规律，有必要从单个胶凝原油颗粒入手，对其开展数值模拟研究。

1 相场模型及求解

胶凝原油在水的悬浮流动中，由于曳力、浮力、粘性力和表面张力等引起的原油颗粒内部对流复杂，并伴随自由界面的变形。研究单个胶凝原油颗粒的运动状态，既要探求其真实的运动轨迹，又要还原运动过程中伴随的变形情况，二者缺一不可。利用N-S方程和相场法耦合可以很好的求解这一问题。本文采用相场法对胶凝原油颗粒的运动进行数值模拟研究，利用相场法可以很好的模拟复杂界面的流动问题。

1.1 物理模型

图1中区域R1为胶凝原油颗粒，颗粒直径半径为0.005 m，C1为流动区域，其中管径为0.053 m，管长为0.3 m。各边界说明如表1所示。

图1 物理模型Fig.1 Physical Model

表1 边界条件Table 1 Boundary Conditions

1.2 数学模型

连续性方程:

动量方程:

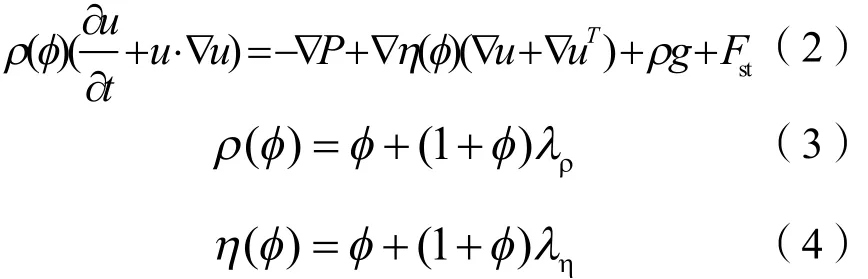
公式1-4中:

u—速度；

t—时间，时间标尺为Lref/uref，（Lref为特征长度。uref为特征速度）；

P—压力；

g—重力加速度；

Fst—表面张力分量;

φ—相场，φ的变化反映出界面形状的变化，当φ=1为模拟的主要对象，如气泡或液滴；

φ=0—气泡或液滴周围的环境流体；

0<φ<1—气液界面；

ρ(φ)—无量纲密度；

λp—密度比；

λp=ρ2/ρ1，ρ1和 ρ2—胶凝原油颗粒和周围流体的密度;

η（φ）—无量纲粘度；

λη—粘度比；

λη=η2/η1, η1和 η2—胶凝原油颗粒和周围流体的粘度。

Cahn-Hilliard方程（简称C-H方程）[5,6]

公式(5)-(8)中：Pe—Peclet数；

Mref—迁移率的标尺；

σ12—界面张力；

M（φ）—迁移率；

μ —化学式；

ε —界面厚度；

2 模拟结果及分析

因数值模拟长距离管道需花费较长时间，本文选取53×300范围为研究对象，利用相场法模拟得到相同速度，相同时间步长，不同油水两相间界面张力系数下的胶凝原油颗粒的流动、变形过程。计算区域采取均匀网格离散，控制方程采用有限元方法离散。管道内的不规则形状为不同时刻下和位置处对应的胶凝原油颗粒。

2.1 不同表面张力系数下的颗粒运动轨迹模拟

表面张力使液体的表面总是试图获取最小的、光滑的面积，使液体的总表面能总是试图达到能量最低的状态，在相场法中，要将表面张力处理成为N-S方程中的力的分量。故本文采取改变表面张力系数的方法观察表面张力对胶凝原油颗粒运动带来的影响。选取油水两相间界面张力系数分别为0.02、0.03、0.08 N/m的单个胶凝原油颗粒为研究对象，连续相与分散相物性如表2所示。选取胶凝原油颗粒半径为0.005 m，运动时间为1.35，经计算得到胶凝原油颗粒运动轨迹（各点时间间隔为 0.15 s）如图2-4所示。

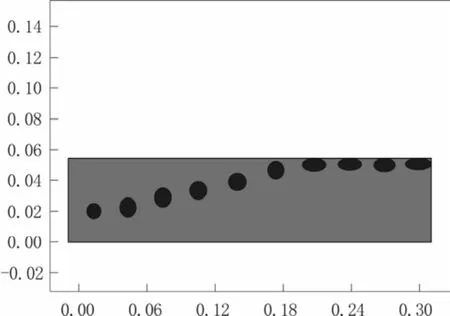
图2 界面张力系数0.02 N/m情况下的胶凝原油运动轨迹Fig.2 The gelled crude oil trajectory of the interfacial tension coefficient is 0.02 N/m

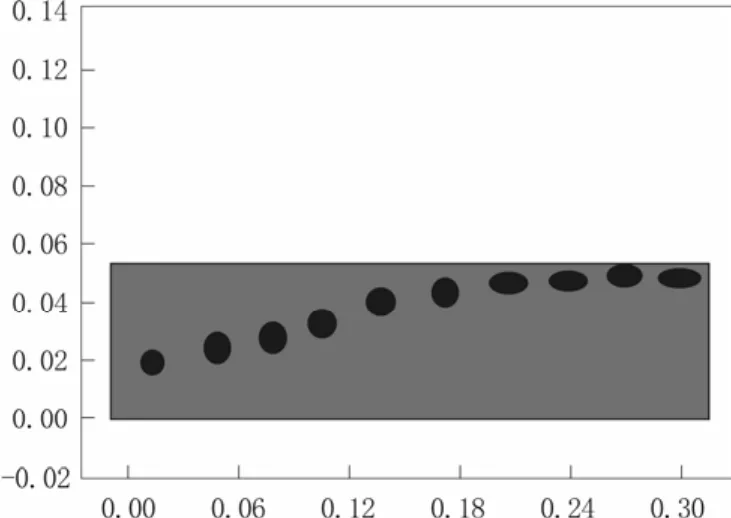
图3 界面张力系数0.03 N/m情况下的胶凝原油运动轨迹Fig.3The gelled crude oil trajectory of the interfacial tension coefficient is 0.03 N/m

图4 界面张力系数0.08 N/m情况下的胶凝原油运动轨迹Fig.4 The gelled crude oil trajectory of the interfacial tension coefficient is 0.08 N/m

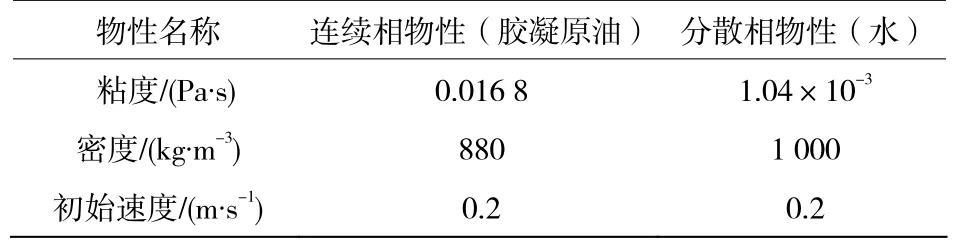
表2 模拟条件Table 2 Simulated Conditions

2.2 分析与讨论

如图2所示，胶凝原油颗粒初始速度与水流速度相同，由于浮力和生力的作用同时向上运动，由于剪切力的作用，在运动的同时伴有变形发生，从而影响原油颗粒所受曳力，进而影响原油颗粒的速度变化。胶凝原油颗粒在运动中由球形逐渐变成椭圆形，在图2和图3，胶凝原油颗粒碰壁后由于受到管壁给予的压力及水流的剪切力，逐渐铺展成片状。但是明显在图3中界面张力系数为0.3 N/m时变形情况较图2有所减弱。如图4所示，随着油水两相间界面张力系数增加，变形情况逐渐减弱。油水两相间界面张力系数为0.8 N/m时，胶凝原油碰壁后的变形亦不明显。不同油水两相间界面张力系数条件下，相同时刻的颗粒运动相对位置基本相同。选取胶凝原油颗粒上均匀分布的上、下、左、右四点为研究对象，得出不同油水两相间界面张力系数下x方向的速度分布如图5-7所示。图5中，由于油水两相间界面张力系数较小，颗粒变形严重，四点的速度整体在0.2 m/s（水流速度）上下震荡，速度变化较为剧烈。图6-7中，各点速度整体同样在0.2 m/s上下变化，随着油水两相间界面张力系数增大，形变减弱，速度变化幅度逐渐较小，且从图中可以观察到，随着颗粒形变的减弱，各点速度有趋于一致的趋势。

3 结 论

本文利用相场法模拟了胶凝原油颗粒的流动变形过程，分析了改变油水两相界面间的界面张力系数对胶凝原油颗粒运动的影响，得到的结论如下：

（1）由于浮力、升力、曳力及水流剪切力作用，胶凝原油颗粒在水中呈上升、悬浮流动状态，碰壁后由于受到管壁的压力作用，颗粒变形严重，逐渐铺展成片状，碰壁后颗粒形变逐渐减弱；

（2）改油水两相间界面张力系数主要影响液滴的形变，对颗粒的运动轨迹影响不大，在胶凝原油颗粒流动过程中，若要保持颗粒形状不变，可通过增大两相间界面张力系数的方法实现。

（3）胶凝原油颗粒上各点的速度在运动中呈不规则变化，且剧烈程度与变形程度有关。变形越剧烈，速度变化越大，形状基本不变后，各点速度趋于一致，近似于水流速度。

图5 界面张力系数0.02 N/m时胶凝原油颗粒各点速度分布Fig.5 The gelled crude oil velocity distributionof the interfacial tension coefficient is 0.02 N/m

图6 界面张力系数0.03 N/m时胶凝原油颗粒各点速度分布Fig.6 The gelled crude oil velocity distributionof the interfacial tension coefficient is 0.03 N/m

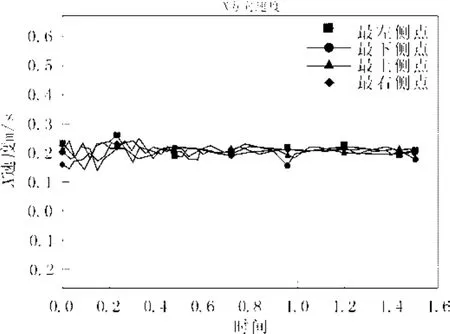
图7 界面张力系数0.08 N/m时胶凝原油颗粒各点速度分布Fig.7 The gelled crude oil velocity distributionof the interfacial tension coefficient is 0.08 N/m

［1］刘晓燕，韩国有，王德喜．特高含水采油期安全混输温度界限试验研究[J].石油学报,2005,26(3):102-105.

［2］刘晓燕，宛辉，韩国有,等．特高含水不加热集油运行管理关键技术[J]. 油气田地面工程, 2007, 26(10): 13-14.

［3］ Liu Xiaoyan，Zhao Bo，Zhang Yan．The Testing Study of The T emperature Limit for Oil-gas-water Mixed Transportation During Oil Production with Special High Water-cut[C].Proceeding of the 3rd IASME/WSEAS Int．Conf．On heat transfer，thermal enginee ring and environment，Corfu，Greece，August 20-22，2005: 49-54.

［4］刘晓燕，陈伟，高海智,等．水-胶凝原油两相流流态化实验研究[J]．工程热物理学报，2013，34(3)：480-483.

［5］石万元, 张凤超, 田小红, 塚田隆夫. 相场法模拟悬浮熔融硅液滴内部对流及自由界面变形现象[J]. 西南交通大学学报, 2012(04):692-697.

［6］DING H,SPELT P D M, SHU C. Diffuse interface model for inco mpressible two-phase flows with large density ratios[J]. J. Comput ational Physics, 2007(2): 2078-2095．