基于元胞自动机模型的人员疏散行为模拟

郭良杰，赵云胜

（中国地质大学工程学院，湖北 武汉430074）

近几年我国灾害频发，如近期发生的雅安地震、吉林宝源丰禽业公司氨气泄漏爆炸火灾以及厦门BRT公交车火灾等。灾害发生后，人员聚集场所的紧急安全疏散再次成为人们关心的问题和研究的热点。国内外针对此方面的研究主要集中在对紧急条件下疏散时间和人员逃生行为特征的研究，但由于实际数据的缺乏和实验准确性的不足，建立人员疏散模型并利用计算机进行仿真模拟已成为研究人员疏散行为的主要手段之一［1］。目前较常用的人员疏散模型有连续型（社会力模型等）和离散型（格子气模型、元胞自动机模型等）之分。本文基于元胞自动机模型对人员疏散过程中的现象和疏散行为进行了定性研究。

1 元胞自动机模型建立

1.1 元胞自动机简介

元胞自动机（Cellular Automata，CA）是由大量简单一致的个体通过局部联系组成的离散、分散及空间可扩展系统，它是在均匀一致的网格上由有限状态的变量（元胞）构成的动力系统［1］。元胞自动机最早由数学家S.M.Ulam和J.von Neumann于1948年提出，最初用于模拟生命系统所特有的自复制现象，是描述自然界复杂现象的简化数学模型［2］。

基本元胞自动机由元胞、元胞状态空间、元胞邻居、元胞规则四部分组成［3］。元胞是其最基本的组成部分，分布在离散的一维、二维或多维欧几里得空间的晶格点上；元胞空间是一种离散的空间网格，常见的有一维和二维两种；元胞状态是取值于一个有限的离散集；元胞邻居是指距离元胞一个半径内的所有元胞。二维元胞自动机常见的邻居类型有von Neumann型、Moore型和扩展Moore型。

1.2 基本元胞自动机模型的建立

本文采用二维元胞自动机模型，将疏散空间划分为均匀的网格，每个网格为一个基本单元。基本单元有被（人、障碍物或墙）占据和空置两种状态。邻居选取von Neumann型，每个元胞处的人员以一定的转移概率（或称偏好矩阵）向其上、下、左、右4个邻居元胞移动或者静止，如图1所示。一个元胞对应的实际空间大小本文取0.4m×0.4m。

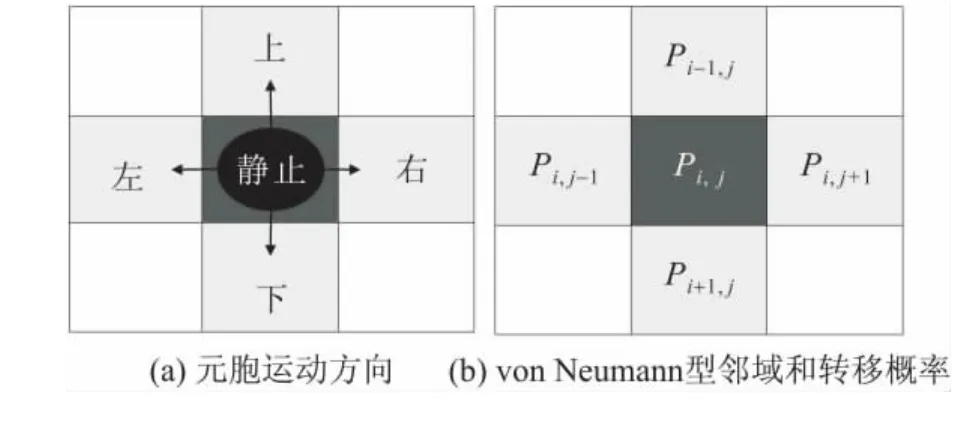
图1 元胞运动方向以及von Neumann型邻域和转移概率Fig.1 Motion direction of the cell and the neighborhood and transition probability of von Neumann

1.3 基于地面场的元胞自动机疏散模型的建立

人员紧急安全疏散研究中应用最为广泛的元胞自动机模型就是地面场模型［4］。地面场模型由C.Burstedde等［5］首次在元胞自动机模型中应用。地面场主要包括静态场和动态场，很多研究者对其扩展加入摩擦、惯性、作用力、障碍物等因素。动态场和静态场及其相关影响因素共同决定了元胞转移概率，此概率决定了元胞下一时刻运动方向，可描述人员下一步行走目标的选择。

中心元胞人员进入单元格（i，j）的概率Pij的计算公式为

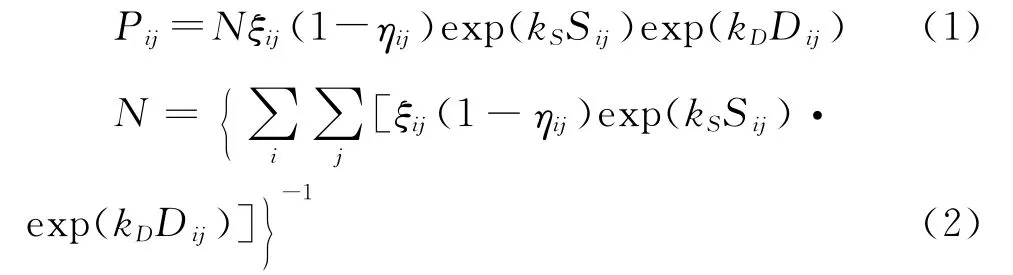
式中：N为正规化因子；kS和kD分别为静态场参数和动态场参数；Sij和Dij分别为静态场强和动态场强；ηij和ξij为元胞状态参数，确定原则如下：

1.3.1 静态场参数

静态场参数是对场所内部结构及场所熟悉程度的描述。静态场强Sij反映了建筑物内的结构和障碍物分布，而参数kS反映了人员对环境的熟悉程度或个体的逃生速度［6—8］。

（1）无障碍物时，Sij的计算公式为

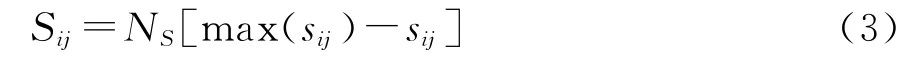
式中：NS为无量纲化因子，计算式类似于公式（2）；sij为（i，j）处元胞到第k个出口的最短距离；i0km和j0km分别为第k出口第m元胞的横、纵坐标。

（2）有障碍物时，常先采用Dijkstra算法找出最短路径，再采用式（3）计算静态场强。

1.3.2 动态场参数

动态场参数是对从众行为的描述。动态场强Dij反映了所有路过（i，j）处动态人员吸引力，而参数kD反映了逃生者对其他逃生者留下的虚拟路径信息的辨识和掌握程度［8］或从众心理的严重程度。其计算步骤如下：

Step1：初始时Dij＝0；

Step2：当有1人从元胞（i，j）处经过，则此处动态场强增加ΔDij，本文取ΔDij＝1；

式中：dtij为未经无量纲化处理的动态场强值；γ和β分别为衰减和扩散系数，分别表示动态场强随时间衰减和向周围元胞扩散的概率，它反映了行人所留下的路径信息随时间扩散和衰减的过程，根据经验本文取分别为上一时刻4个邻域动态场强。

Step4：对dtij进行无量纲化处理得Dtij，有

为了消除个体留下的动态场强对自身的影响，C.Burstedde等［5］提出了如下一步修正算法：

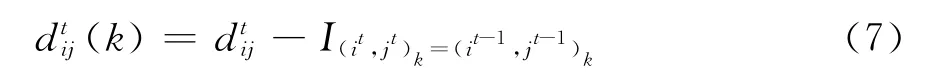
式中：I（it，jt）k＝（it－1，jt－1）k为指示函数，（it，jt）k和（it－1，jt－1）k分别为个体k在t和t－1时刻的位置，两者相等时指示函数I为1，否则为0。

上述方法仅修正一步，衰减较慢时效果仍不理想。对此，程远［8］做了完全修正，即用表示个体k在（i，j）处产生的动态场强，而表示除k外其他个体产生的动态场强。考虑到程序的易实现性，本文采用公式（7）的一步修正算法。

1.3.3 排斥和摩擦概率

排斥和摩擦概率是对躲避潜在伤害行为的描述。图2为人员疏散中存在排斥力和摩擦力的几种情况。对此宋卫国等［9］和于彦飞［10］引入了排斥和摩擦概率，为了便于研究此行为对疏散的影响大小，本文加入kr和kf两个参数，如下式：

式中：pr和pf分别为排斥和摩擦概率，即行人在上述情况下分别以概率pr和pf静止；kr和kf分别为调节影响大小的参数；α和θ分别为硬度系数和摩擦系数，α∈［0，∞］，θ∈［0，1］；v为相对速度。

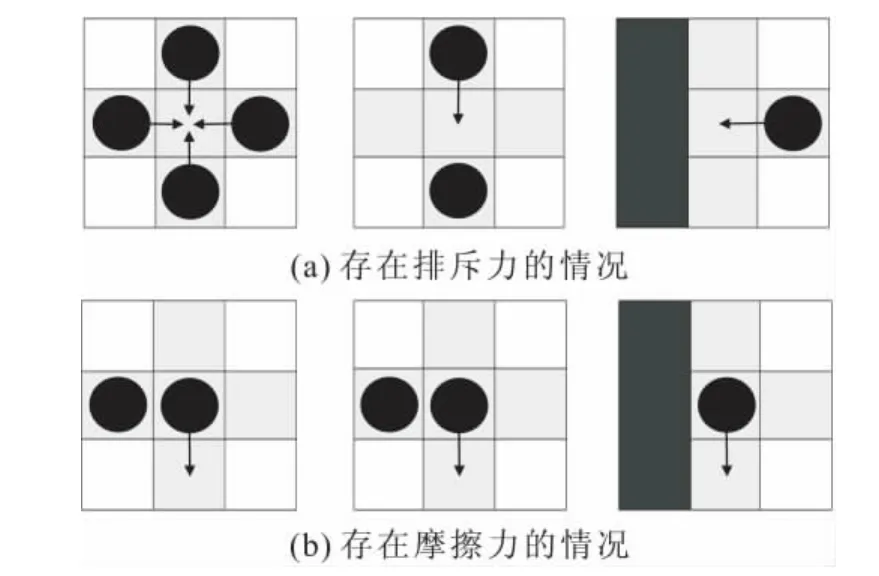
图2 人员疏散中存在排斥力和摩擦力的几种情况Fig.2 Friction force and repulsive force in the motion states

1.3.4 其他行为描述

（1）惯性行为描述：在计算目标选择概率时加入惯性作用影响参数ω，其中ω＞1，即在式（1）求得Pij的基础上乘以一个大于1的参数，有

式中：P′ij为该时刻疏散人员在上一时刻运动方向（即惯性方向）上的目标选择概率。

（2）竞争行为描述：当多人同时竞争进入同一目标时，所有人进入概率相等，最终进入的人从所有人中随机产生。

（3）跌倒和拥挤行为描述：引入随机慢化规则，即所有人员都以小概率p静止。p的大小与人员期望疏散速度和室内人员密度有关。

2 仿真模拟

基于以上建立的模型，利用MATLAB编写模拟软件，其界面如图3所示。除特殊说明外，模拟参数设置为：kS＝1、kD＝0.5、kf＝kr＝0.5、θ＝0.1（人与人）、θ＝0.3（人与墙）、α＝1（人与人）、α＝1.5（人与墙）、ω＝1.2、p＝0.05、β＝0.2、γ＝0.2，期望疏散速度v＝2.0m/s，则一个时间步长为0.2s。为了保证结果的科学性，模拟结果皆为多次模拟所得。

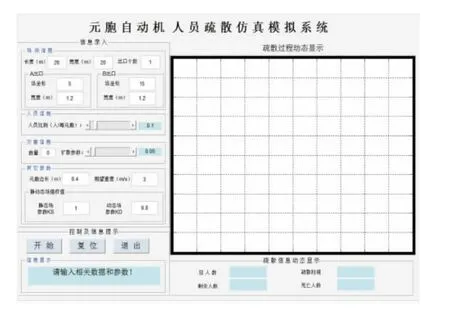
图3 模拟软件界面Fig.3 Simulation software interface

2.1 基本场景模拟

2.1.1 场景描述

图4为利用模拟软件模拟得到的人员疏散过程动态显示截图。图中a和b是两相同房间，长、宽分别为12m和8m，出口的宽度为1.2m，每个房间内随机分布约100人，其中b房间内障碍物的长、宽分别为4m和1.2m。

2.1.2 模拟结果分析

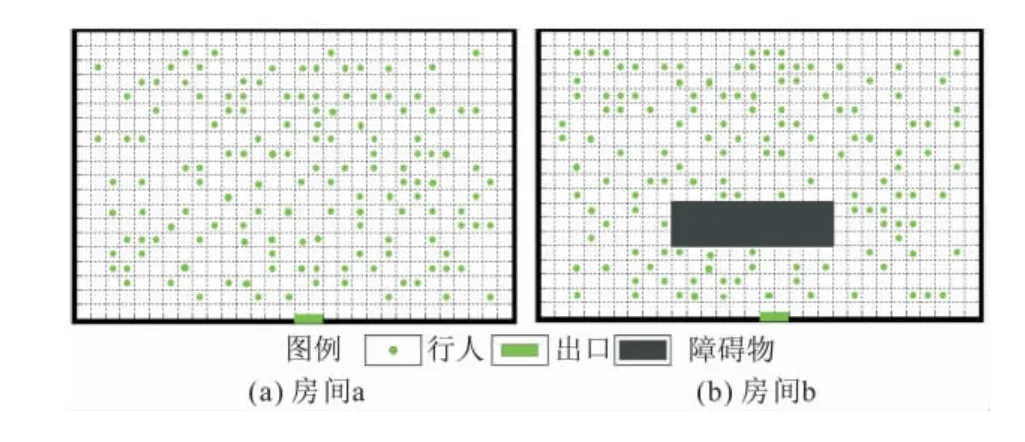
图4 房间a和b内初始人员分布Fig.4 Initial distribution of the personnel in rooms a and b

（1）初始静态场和转移概率场分布。图5为两个房间的静态场强分布，为了便于观察，将该图水平旋转180°，从图中可见障碍物的存在影响了静态场的分布，使得在障碍物远离出口的一边出现了一个左右绕行分界线。

图5 房间a和b的静态场强分布图Fig.5 Distribution of static floor field intensity in rooms a and b

图6为0.2s时房间b中人员转移概率分布，图中出口所在方向为下方。由图6可知，人员下移概率普遍大于上移概率；人员左、右移动概率出现了分界线，障碍物上方分界线是绕行线，下方是房间的中线，这说明往出口方向以及绕行障碍物方向人员移动的概率是最大的，较符合实际。

图6 0.2s时房间b中人员转移概率分布图Fig.6 Probability distribution of transferring to the motion direction at 0.2s

（2）两房间疏散时间比较。保持期望疏散速度不变进行多次模拟，发现房间b比房间a的平均疏散时间长，这说明出口处障碍物的存在对人员疏散有阻碍作用。

（3）不同期望疏散速度下的人员聚集和“欲速则不达”现象。①人员聚集现象：不同期望疏散速度会产生不同的人员聚集现象［9—10］，图7为房间a在不同期望疏散速度下的人员聚集情况。由图7可以看出：当期望疏散速度为1m/s时，出口较为通畅，基本没有出现堵塞［见图7（a）］；当期望疏散速度为3m/s时，出口轻微堵塞［见图7（b）］；而当期望疏散速度为5m/s时，出口堵塞稍严重，部分远离出口处出现了人员绕行行为［见图7（c）］。②“欲速则不达”现象：不同期望疏散速度的疏散时间也存在着差异，图8为不同期望疏散速度下的疏散时间变化情况。由图8可以看出：期望疏散速度从1m/s增加到5m/s过程中疏散时间先减小后增加。可见，适当地增加疏散速度会使疏散加快，但是当超过某个值时，疏散反而变慢，这是因为随着行人速度的增加，人与人、人与障碍物之间的作用力增加，且易造成出口严重堵塞，从而使得疏散时间增加。

图7 不同期望速度下的人员聚集情况Fig.7 Clustering phenomena at different expected speeds

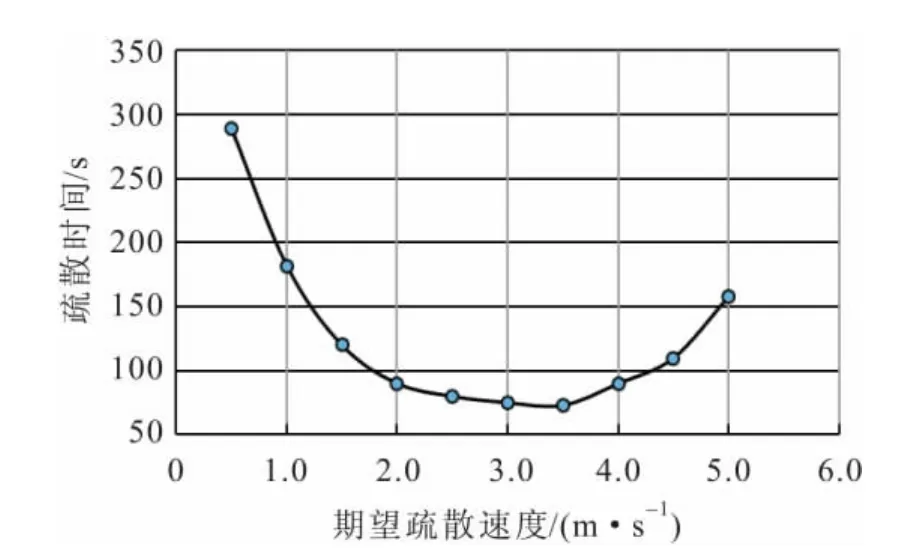
图8 不同期望疏散速度下的疏散时间变化情况Fig.8 Evacuation time change at different expected evacuation speeds

2.2 复杂场景模拟

2.2.1 场景描述

图9为某超市简化平面图及初始人员分布图。该超市长、宽分别为48m和28m，两出口宽度均为3m，室内随机分布约1 000人，期望疏散速度取3 m/s。

需要说明的是，本文将超市内人数设置为1 000人以及将出口设置为两个，主要是为了研究的需要。实际上超市中人数一般是低于1 000人的，同时出口也不止两个，一般还有应急出口。

图9 某超市平面图及初始人员分布图Fig.9 Plan of a supermarket and the initial distribution of the personnel

2.2.2 模拟结果分析

经过多次模拟，得到如图10所示的较具有代表性的人员疏散情况。基于图10做以下分析：

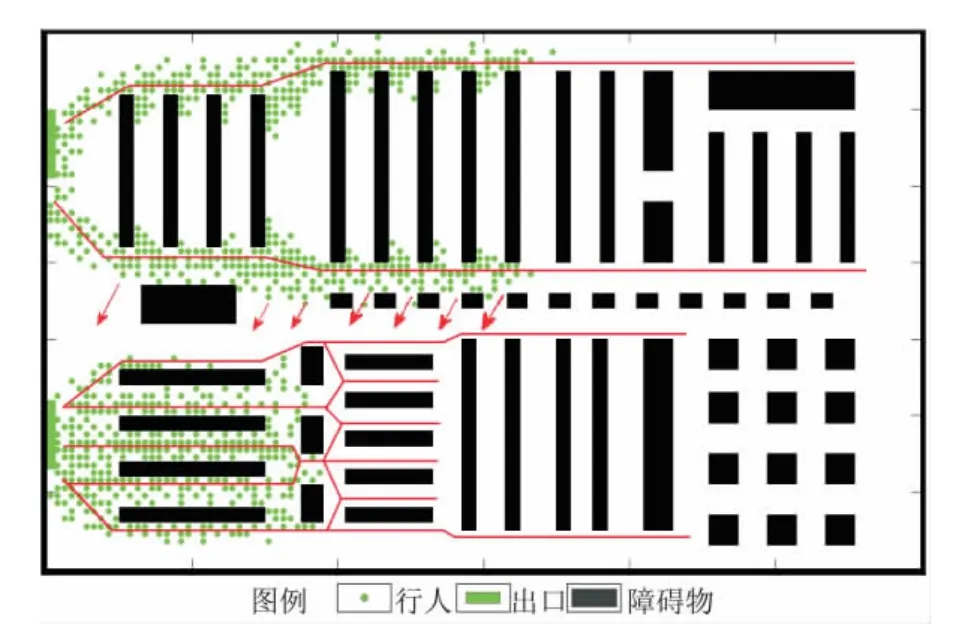
图10 某超市人员疏散情况仿真模拟Fig.10 Analogue simulation of evacuation situation in the supermarket

（1）出口处障碍物的布置对人员疏散的影响。两个出口处障碍物的个数和总面积是相等的，只是摆放方向不同。多次模拟发现，下方出口的人员疏散情况明显优于上方出口，说明出口处的障碍物相对出口纵向放置比横向放置更有利于人员疏散。

（2）从众效应。将kD的大小增加至1.5，kS减小至0.6，此时人员对环境的熟悉程度降低，而从众心理较为严重。图10为多次模拟出现的较有代表性的典型从众效应模拟结果。图中红色直线是根据动态场强的分布而粗略绘制的人员疏散轨迹。由于被疏散人员的从众心理过于严重，相对忽略了自己对环境的认识，使得人员过分地跟随前人的轨迹（即直线轨迹）行走，降低了自身的能动性，从而出现了拥挤的人流队列，同时这也导致箭头所在空闲区域没有被利用，而箭头上方区域却形成了拥挤的队列，造成疏散路径和疏散出口都没有被合理利用，降低了疏散效率。

为了进一步研究环境熟悉程度较低情况下的从众效应对人员疏散的影响，将kS的大小降低至0.5且保持不变，研究不同kD大小下的平均疏散时间。结果发现：当kD＝0即完全没有从众心理时，疏散时间为592.4s，kD＝0.7时的疏散时间为620.6s，并且发现将kD的大小从0增加至1的过程中，平均疏散时间呈先减小后增加的趋势。以上结果表明在对环境的熟悉程度不是很高时，适当的从众心理是有利的，而从众心理过于严重将不利于人员疏散。

3 结 论

基于元胞自动机模型对人员疏散行为进行仿真模拟，可以得到以下结论：

（1）当人们选择不同的期望疏散速度时，会在出口形成不同程度的人员聚集现象。

（2）人员疏散中存在“欲速则不达”现象，适当的增加期望疏散速度会使人员疏散加快，但是期望疏散速度过大时疏散反而变慢。因此，在发生紧急情况时，应注意引导人们合理选择步行速度，过慢或过快都不利于人员疏散。

（3）障碍物（特别是出口处障碍物）对人员疏散会造成阻碍作用，且相对出口横向放置的障碍物的阻碍作用要大于纵向放置。因此，在商场、超市等人员聚集场所，货物要尽量相对出口纵向放置，以最大限度地降低障碍物对人员疏散的阻碍。

（4）在对环境熟悉程度不高，或紧急情况下造成对环境的判断能力降低时，适当的从众心理有利于最优疏散信息的传递，可以帮助人们找到最佳疏散路径；但从众心理过于严重则易因盲从造成出口利用率降低或利用不平衡。因此，公共场所的设计中可以在不能合理利用的路径安排引导人员或设置指示标志，以便在疏散时帮助人们选择合理的疏散路径。

［1］赵道亮.紧急条件下人员疏散特殊行为的元胞自动机模拟［D］.合肥：中国科学技术大学火灾科学国家重点实验室，2007.

［2］von Neumann，J.TheoryofSelf－reproductionAutomata［M］.Urbana，IL：University of Illinois Press，1966.

［3］段晓东，王存睿，刘向东.元胞自动机理论研究及其仿真应用［M］.北京：科学出版社，2012.

［4］Zheng，X.P.，T.K.Zhong，M.T.Liu.Modeling crowd evacuation of a building based on seven methodological approaches［J］.BuildingandEnvironment，2009，44（3）：437－445.

［5］Burstedde，C.，K.Klauck，A.Schadschneider，et al.Simulation of pedestrian dynamics using a two－dimensional cellular automaton［J］.PhysicaA：StatisticalMechanicsandItsApplications，2001，295（3/4）：507－525.

［6］Kirchner，A.，A.Schadschneider.Simulation of evacuation processes using a bionics－inspired cellular automaton model for pedestrian dynamics［J］.PhysicaA：StatisticalMechanicsand ItsApplications，2002，312（1－2）：260－276.

［7］Peng，Y.C.，C.I.Chou.Simulation of pedestrian flow through a“T”intersection：A multi－floor field cellular automata approach［J］.ComputerPhysicsCommunications，2011，182（1）：205－208.

［8］程远.基于演化博弈论的群体疏散行为研究［D］.北京：北京化工大学，2012.

［9］宋卫国，于彦飞，范维澄，等.一种考虑摩擦与排斥的人员疏散元胞自动机模型［J］.中国科学－E辑 －工程科学－材料科学，2005，35（7）：725－736.

［10］于彦飞.人员疏散的多作用力元胞自动机模型研究［D］.合肥：中国科学技术大学，2008.

［11］郑营.基于元胞自动机模型的火灾环境下人员疏散研究［D］.北京：北京交通大学，2011.

［12］张莉.基于地铁火灾仿真的人员疏散研究［D］.上海：同济大学，2008.

［13］孙宽.基于运输模型的安全疏散方案优化方法探讨［J］.安全与环境工程，2010，17（3）：74－77.