基于子孔径拼接法测量高精度反射镜

郑立功

（中国科学院 长春光学精密机械与物理研究所 中国科学院 光学系统先进制造技术重点实验室，吉林 长春130033）

引言

大口径光学平面镜的检测，在传统光学检测中，通常需要配备大口径干涉仪或者搭建Ritcheycommon形式的检验光路［1-2］，这时往往需要一块与被检元件尺寸相同甚至更大尺寸的参考光学平面或球面，然而制造和检测大口径参考平面镜和球面镜存在很多的困难，并且所需的时间很长，费用也很昂贵。

子孔径拼接技术作为一种有效的大口径光学镜面检测手段，最早于1982年由C.J.Kim提出，该技术用一系列较小的光学平面阵列代替了较大的参考平面，从而实现对大型光学系统的检测。在国外，QED公司与亚利桑那大学光学中心对该技术进行了比较深入的研究。2003年，QED公司成功研制了自动拼接干涉仪，同时其基于VON（variable optical null）技术［3］，成功实现了对大偏离量凸非球面的子孔径拼接检测。亚利桑那大学光学中心基于 ML（maximum likelihood）算法，在标准参考镜存在较大面形误差的情况下，对1.6m光学平面镜实现了拼接检测［4］。

国内自上世纪90年代以来也有多家单位对此进行了研究，其中长春光机所实现了对非球面的拼接检测［5-6］；南京理工大学将子孔径技术应用到了相移平面干涉仪中［7］；四川大学成功搭建了一套子孔径拼接检测实验系统［8］。

本文基于最小二乘拟合提出了一套拼接算法，由标记点标定完成了子孔径间的对准，实现了对Φ120mm口径平面镜拼接。同时通过将拼接结果与全口径检测结果与自检检测结果进行对比，对拼接结果进行了误差分析。

1 子孔径拼接的数学模型与拼接算法

1.1 子孔径数据采集与坐标变换

子孔径拼接是指依据被检面的面形参数及干涉仪的技术参数将被检面划分为若干个子区域，对各子区域单独检测，再将检测结果拼接合并，从而获得整个被检面面形信息的检测方法。如图1所示，w1与w2分别代表两次干涉仪在待测光学镜面上检测区域，它们之间有一定面积的重叠（重叠区域面积不小于子孔径面积的25%），每个子孔径对应的相位分布用（x1、y1、z1）与（x2、y2、z2）表示（相位分布可以由Zygo干涉仪测得），由于2个子孔径间存在一定的位置关系（该位置关系可以通过靶标标定或者由2个孔径间的机械移动读取），对于光学平面镜的测量，2个子孔径间的位置关系可以用平移与旋转来表示，假设孔径2相对于孔径1有一个x方向的平移dx，一个y方向的平移dy，并且绕某一点（rx、ry）逆时针旋转了θ角度。

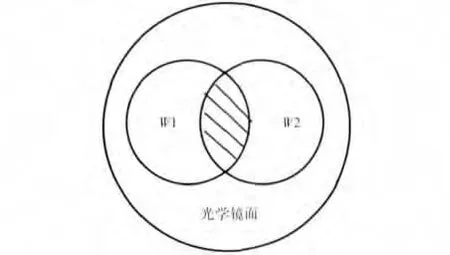
图1 子孔径示意图Fig.1 Two sub-apertures with a common area

以孔径1为基准建立全局坐标系，孔径2在全局坐标下的坐标表示为（x2’、y2’、z2’），由齐次坐标变换理论［9］，得到：

其中：

计算可得：

在子孔径检测中，利用标记点或靶标标定确定各子孔径间的相对位置关系，基于上述理论实现各子孔径间对准，通过选择基准子孔径，从而完成子孔径全局坐标的统一。

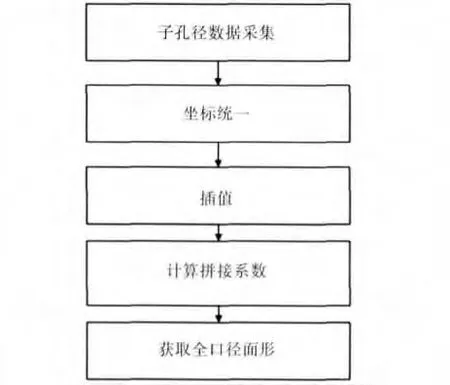
图2 拼接算法流程图Fig.2 Flow chart of stitching algorithm

1.2 拼接系数的求解与多个孔径拼接

利用重叠区域检测数据求解相邻子孔径间的相对调整误差，可以实现子孔径两两拼接。通过重复利用子孔径两两拼接原理就可以实现多个子孔径的拼接。但是这样会造成误差传递和累积，从而降低整个孔径的检测精度［7］。因此，在拼接中采用综合优化的拼接算法，子孔径算法流程图如图2所示。

首先，完成对子孔径相位信息的采集，依据各子孔径间的相对位置，采用上述方法实现子孔径的全局坐标统一，并定义插值点，通过三角剖分插值算法［10-11］获得插值点在不同子孔径内计算所得的相位值，计算各子孔径相对于参考子孔径的拼接系数。

假设共有N个子孔径，以第N个子孔径为基准子孔径，第i个子孔径的相位值可以表示为

式中：wi为第i个子孔径检测数据；pi、ai、bi分别对应第i个子孔径对应的平移与倾斜系数。由于不同子孔径在重叠区域应该检测到相同的相位值，基于最小二乘拟合算法，则

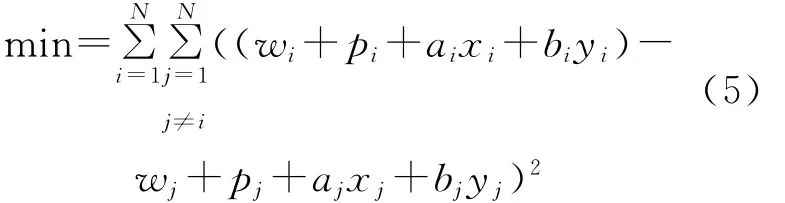
（5）式可以写为

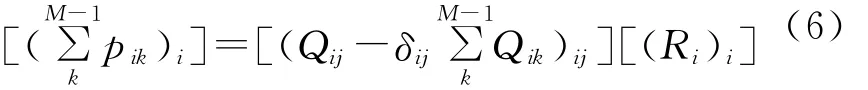
式中，矩阵P、Q、R分别为

（7）式～（8）式中的求和是在重叠区域进行的，若两子孔径wi和wj间没有重叠部分，则子矩阵Pij、Qij为零矩阵。通过（6）式～（11）式即可求得各子孔径拼接系数矩阵Ri，即可实现被检镜面的全口径面形重建。

2 子孔径拼接实验及结果

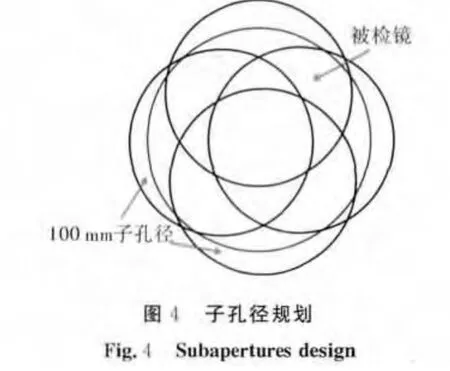
为了验证上述算法对高精度平面镜的拼接精度，对口径Φ120mm平面镜进行了拼接验证实验。检测装置如图3所示。其中利用口径Φ100mm 4个子孔径对被检测面形完成了全口径覆盖，子孔径规划如图4所示。子孔径检测结果如图4所示。

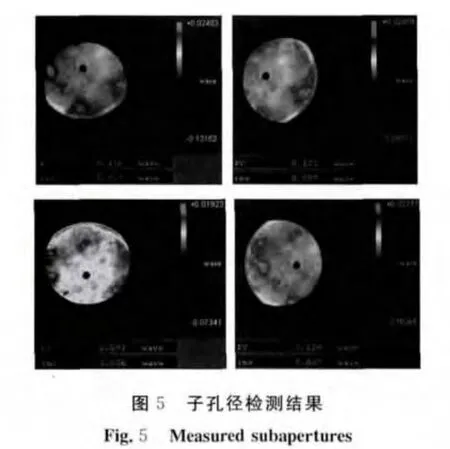
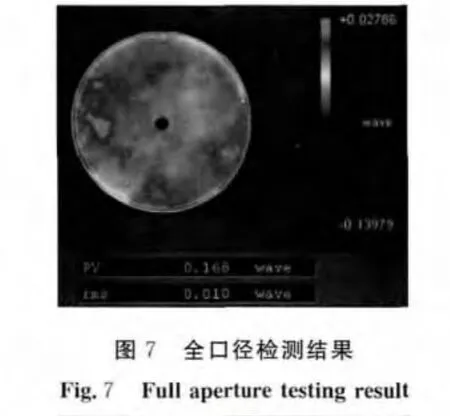
拼接中，基于标记点实现了各子孔径间的对准及全局坐标统一。如图5所示，标记点在各子孔径检测结果中体现为一圆形区域（该区域内检测结果为No Data）。各子孔径内该圆形区域应位于全局坐标内同一位置，基于该区域实现各子孔径X方向及Y方向的对准，从而完成各子孔径全局坐标的统一。在拼接算法中，采用三角剖分插值［10-11］。拼接结果如图6所示。同时基于2种方法对拼接精度进行了误差分析。首先，利用口径Φ150mm干涉仪对被检镜面进行了全口径面形测量，测量结果如图7所示。将全口径测量结果与子孔径拼接结果进行点对点相减，得到2次检测结果的残差图如图7所示。由图8可以看到残差图面形光滑连续，其PV（peak-to-valley）值与 RMS（root-mean-square）值分别为0.020λ与0.002λ。

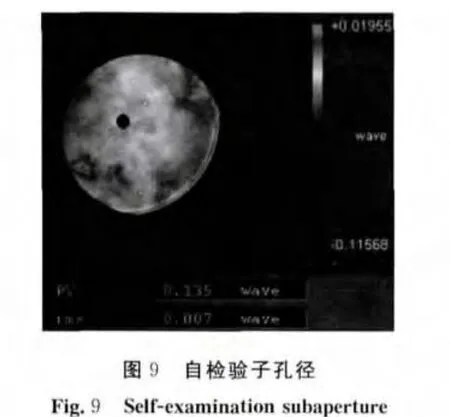
在实际检测中，通常并不能直接获得被检镜的全口径面形，特别是对大口径平面镜与凸非球面镜。此时可以通过自检验的方式对拼接精度进行分析。自检验即利用子孔径检测信息对拼接结果进行精度分析。通过分析拼接结果与自检验子孔径检测结果在自检验子孔径区域的残差从而对拼接精度进行评价。其中自检验子孔径检测结果如图9所示，自检验子孔径与拼接结果残差图如图10所示。由图10可以看到其PV与RMS值分别为0.011λ与0.002λ。亦验证了拼接算法在检测高精度平面镜时的可靠性与准确性。

3 结论

本文基于最小二乘拟合拼接算法，利用标记点标记的方式实现各子孔径的对准，利用Φ100 mm干涉仪对Φ120mm平面镜实现了拼接检测，拼接结果光滑连续，无狭缝。同时分别利用全口径检测结果与自检验的方式对拼接结果进行误差分析，其与全口径PV值与RMS值的偏差分别为0.020λ与0.002λ，与自检验子孔径PV 值与RMS值的偏差分别为0.011λ与0.002λ，验证了本文所述方法的可行性。本文所述技术具有检测精度高与设备要求简单等诸多优点，为高精度平面反射镜的拼接检测提供了一种有效可行的方法。

［1］ 李新南，张明意.大口径光学平面的子孔径拼接检验研究［J］.光学技术，2006，32（4）：514-517.LI Xin-nan，ZHANG Ming-yi.Study on the sub-aperture stitching interferometry for large plane optics optical technique［J］.Optical Technique，2006，32（4）：514-517.（in Chinese with an English abstract）

［2］ 张明意，李新南.子孔径拼接法检测大口径光学镜面精度分析［J］.应用光学，2006，27（5）：446-449.ZHANG Ming-yi，LI Xin-nan.Accuracy analysis of stitching interferometry for test of large-diameter mirror［J］.Journal of Applied Optics，2006，27（5）：446-449.（in Chinese with an English abstract）

［3］ PAUL MURPHY，GARY DEVRIES，FLEIG J，et al.Measurement of high-departure aspheric surfaces using shubaperture stitching with variable null optics［J］.SPIE，2009，7426：74260P.

［4］ SU Peng.Absolute measurements of large mirrors［D］.Arizona：The University Of Arizona，2008.

［5］ 王孝坤，郑立功，张学军，等.子孔径拼接干涉检测离轴非球面研究［J］.光子学报，2011，40（1）：92-97.WANG Xiao-kun，ZHENG Li-gong，ZHANG Xuejun，et al.Testing an off-axis asphere by subaperture stitching interferometry［J］.Acta Photonica Sinica，2011，40（1）：92-97.（in Chinese with an English abstract）

［6］ 王孝坤.利用子孔径拼接法测量大口径凸面反射镜［J］.应用光学，2013，34（1）：95-100.WANG Xiao-kun.large convex mirror measurement by subaperture stitching interferometry［J］.Journal of Applied Optics，2013 ，34（1）：95-100.（in Chinese with an English abstract）

［7］ WANG Q，CHEN J B，ZHU R H，et al.A new technique for testing large optical flat［J］.SPIE，1993 ，2003：389-397.

［8］ 张蓉竹，石琪凯，蔡邦维，等.子孔径拼接干涉检测实验研究［J］.光学技术，2004，30（2）：173-175.ZHANG Rong-zhu，SHI Qi-kai，CAI Bang-wei.Subaperture stitching interferometry detection experimental［J］.Optical Technology，2004 ，30（2）：173-175.（in Chinese with an English abstract）

［9］ 王孝坤，王丽辉，张学军.子孔径拼接干涉法检测非球面［J］.光学精密工程，2007，15（2）：192-198.WANG Xiao-kun，WANG Li-hui，ZHANG Xue-jun.Testing asphere by sub-aperture stitching interferometric method［J］.Optics and Precision Engineering，2007，15（2）：192-198.（in Chinese with an English abstract）

［10］ 闫力松，王孝坤，罗霄，等.采用三角剖分算法的子孔径拼接检测技术［J］.红外与激光工程 ，2013，42（7）：1793-1797.YAN Li-song，WANG Xiao-kun，LUO Xiao，et al.Subaperture testing technology based on triangulation algorithm［J］.Infrared and Laser Engineering，2013，42（7）：1793-1797.（in Chinese with an English abstract）

［11］ YAN Li-song，WANG Xiao-kun，ZHANG Li-gong，et al.Experimental study on subaperture testing with iterative triangulation algorithm［J］.Optics Express，2013，21（19）：22628-22644.