萤火虫算法在化工过程优化中的应用

常晓萍

杜文芳②

王凌②

何学甫②

（①武汉轻工大学电气与电子工程学院，武汉430023；②武钢氧气公司，武汉430083）

0 引言

许多化工过程中定态优化问题都属于非线性约束问题，在对其进行解决的时候通常采用常规经典数学方法，如广义梯度法和逐次二次规划法等。由于在化工领域的优化求解中此方法取得了良好的效果，从而得到广泛的应用[1]。

近些年以来，萤火虫算法、蚁群算法以及粒子群算法等群智能优化算法由于具有强大的寻优能力而得到了广泛的应用。该算法将待优化问题的所有可能解看成一个解空间，从一个随机的可能解开始，通过对该子集施加算法而产生新解集，最终达到最优解的状态。由于此算法在寻优过程中不受搜索空间连续或可微的限制，只需要目标函数的信息，因此具有良好的应用前景。

1 萤火虫算法原理

萤火虫算法（GSO）属于群智能算法之一，是由印度学者Krishnanand等人[2]在2005年提出的。每只萤火虫在GSO算法中分布在目标函数的定义空间中，这些萤火虫除了自带的荧光素外还拥有各自的视野范围，即区域决策范围。其所处位置的目标函数值对其亮度具有很大的影响，越亮的萤火虫表明所处位置越好，即拥有较好的目标值。在区域决策范围内，萤火虫都会寻找邻居集合，萤火虫越亮拥有的吸引力越高，从而吸引其他萤火虫向此方向移动。邻居数量会影响其区域决策范围的大小，为了利于找到更多的邻居，当邻居密度较低时就会加大决策半径，反之则减小决策半径，最终在较优点处聚集大部分的萤火虫。

在萤火虫算法中最重要的两个要素是亮度和吸引度：亮度除了体现萤火虫所处位置的优劣外，还决定了其移动的方向；吸引度则决定了萤火虫的移动距离，为了达到目标最优的效果，可通过不断更新亮度和吸引度来实现。

设I为萤火虫的相对亮度，数学表述为

式（1）中，I0为萤火虫的最大荧光亮度与优化问题中的目标函数相对应，目标函数越优，亮度越高；q为光强吸收系数，体现荧光因距离的增加和传媒媒介的吸收逐渐减弱；rij为萤火虫i与j之间的距离。

萤火虫的吸引度表述为：

式（2）中，β0为最大吸引度。

萤火虫i被吸引向萤火虫j移动的位置更新由下式决定：xi（t+1）=xi（t）+β×（xj（t）-xi

式（3）中，xi（t）和xj（t）为萤火虫i和j所处的空间位置；ε为步长因子，一般选取[0,1]之间的常数；rand为[0,1]上服从均匀分布的随机因子。

2 实例仿真

本文在进行优化仿真的时候以苯—甲苯闪蒸过程[3]为例。流程图如图1所示。

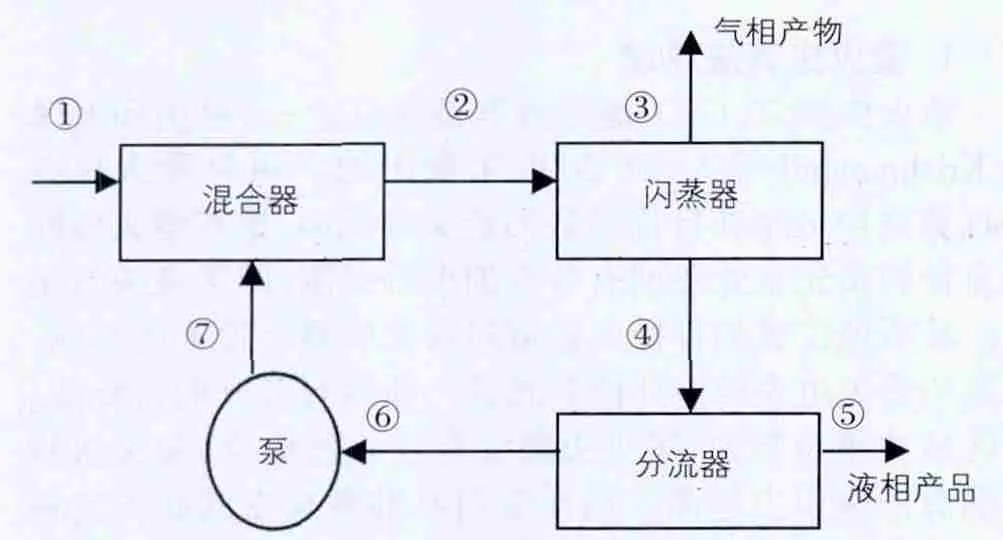
图1 苯-甲苯闪蒸过程

如图1所示，闪蒸器在此过程中，顶部输出气象产物，底部输出的流向分流器，除了一部分作为液相产品外，另一部分进入泵作为循环回流，由于与新鲜料液在混合器进行混合后进入闪蒸器从而提高了苯的回收率。

在进程①中，新鲜物料的状态如下：温度和压力分别为 110℃和 1.818×105Pa；苯和甲苯的流量均为 50kmol·h-1，可将此混合物认定为理想体系。优化的目的就是使得汽相产物中苯的产量最大，对此，可以通过调整闪蒸温度、压力、分流器操作分类系数即进程⑤对进程④的流量比实现。优化问题的数学模型参见文献[4]。采用Matlab语言编制的算法进程由于加入了记忆功能，从而避免了优化解的遗失，最终实现了算法的智能化。由于缩短了寻优过程和节省了计算时间，从而有效提高了程序运行的效率。

仿真程序设计如下：①初始化基本参数，主要是萤火虫数目m，最大吸引度β0，步长因子ε，迭代次数s及搜索精度等。萤火虫数目m对应优化变量X的解空间的数目，其规模大小决定每一次向吸引度强的位置趋近时解空间的多少，可以相应地计算出对应的目标函数。②随机给出一组萤火虫的初始位置，即变量X的一组初值。并计算出相应的萤火虫的荧光亮度，即目标函数。③计算萤火虫的相对亮度和吸引度，根据相对亮度决定萤火虫的移动方向。即根据步骤②中随机选取的变量X的初值，计算目标函数的值。④更新萤火虫的位置，即根据步骤③所计算出的目标函数值的优劣，重新选择变量X。如该次目标函数优于前次值，则保留该次变量X之值，反之舍去，重新更新位置，选取新的变量X值，进入迭代循环。⑤检查是否满足迭代条件，满足，结束程序运行，输出优化解和相应的目标函数。计算过程中，萤火虫数目取20个，光强吸收系数q=1.0，最大吸引度β0=1.0，步长因子ε=0.02，迭代次数s取300。

仿真运行5次，结果如表1所示，表2为各进程的优化操作条件，分流系数为0.5262，各符号意义如下：

F—流量，（kmol·h-1）；H—焓，（J）；p—闪蒸压力，（Pa）；T—温度，（℃）；x—摩尔分数；f(x)—目标函数（气相产物中的苯含量），（kmol·h-1）。下角标 b 表示苯；t表示甲苯；1，2，…，7分别代表图1中的进程序号。

3 结语

本文在对苯-甲苯闪蒸过程中进行优化仿真计算时采用GSO算法，采用此算法具有很好的遍历性，不仅能够有效对优化对象进行求解，还能够得到比经典数学方法更优化的结果。采用经典方法得出的结论为：闪蒸温度和闪蒸压力分别为95.0032℃和1.087×105Pa，进程③的流量和最优苯产量分别为 3.6583kmol·h-1和 2.5740kmol·h-1。这组数据充分证明了采用萤火虫算法能够有效地对化工生产过程[5]中的优化问题进行解决。

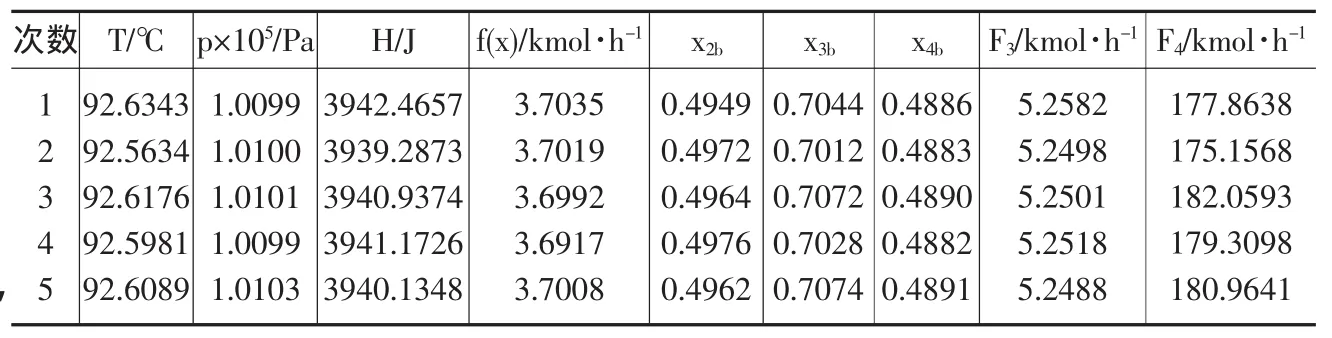
表1 优化仿真结果

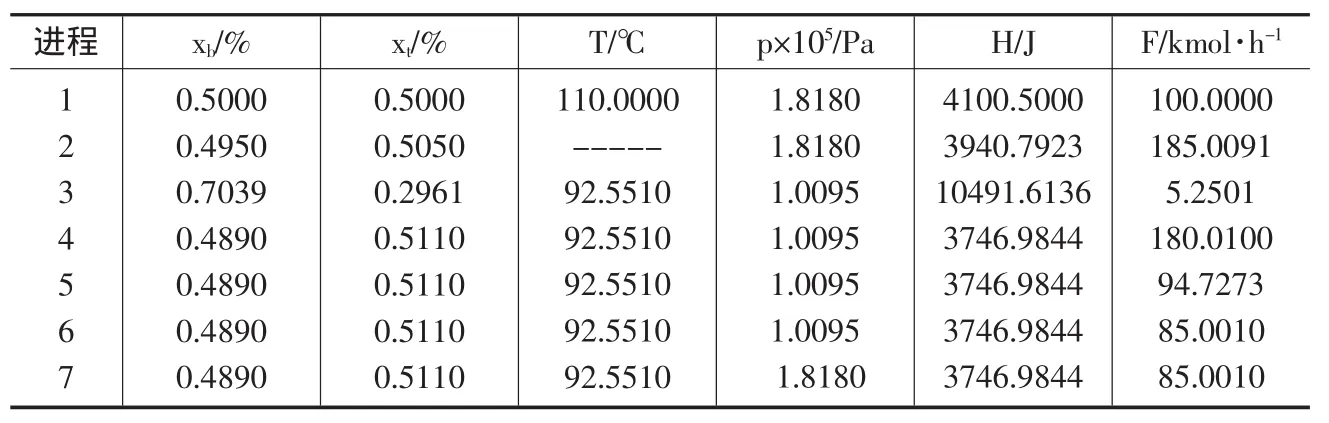
表2 各进程优化值

[1]姚平经.化工过程系统工程[M].大连：大连理工大学出版社,1992.

[2]KRISHNANAND K N,GHOSE D.Detection of multiple source locations using a glowworm metaphor with applications to collective robotics[C].Proc of IEEE Swarm Intelligence Symposium.Piscataway:IEEE Press,2005:84-91.

[3]骆晨钟,张志强,邵惠鹤.混沌搜索方法及其在化工过程优化中的应用[J].化工学报,2000,51（6）：757-760.

[4]邓正龙.化工中的优化方法[M].北京：化学工业出版社,1992.

[5]王克峰,修乃云,匡国柱等.非线性蒸汽动力系统参数优化新方法——改进遗传算法[J].化学工程，1998,26（4）:42-45.