国内35个大中城市房价指数预测

李 建，庄 健

（安徽工业大学 商学院，安徽 马鞍山243002）

进入21世纪以来，全国大部分地区的房价一直呈上升趋势，其中大中型城市的房价上涨趋势尤为明显。政府一直强调和重视房价稳定，为此出台多项稳定房地产市场的政策和措施。要科学调控房地产市场，稳定房地产价格，最为基础是要找出房地产价格变化规律，加强对房地产价格的预测。

一、文献回顾

学术界从来就没有停止对房地产价格规律的认识，许多学者一直在寻求有效预测房地产价格指数的方法。房价指数的时间序列预测始于Case和Shiller，他们对美国大都会地区的房价指数做了预测，证明了房价指数是可测的。［1］Muellbauer和 Murphy考察了英国房价的变化，发现房价与天气、家庭收入和地区有相互关联的作用，［2］在Ortalo-Magne和Rady开发的模型中引入了房产制度，从而使模型具有复杂的非线性动态行为。［3］G.W.Crawford和 M.C.Fratanton尝试用ARIMA模型、GARCH模型和regime-switch模型对美国的五个地区的92个季度房价指数增长率进行了建模和预测实验。结果发现，在拟合方面，regime-switch模型精度略高，但在预测时，简单的ARIMA模型更为精确。［4］

我国房价和房价指数时间序列的预测在预测模型上呈现多样性，这里列举具有代表性的文献。王婧和田澎用小波神经网络对上海的中房住宅指数的月度数据进行了预测。［5］杨楠和邢力聪用灰色马尔科夫模型对中房上海住宅指数做了预测。［6］谈萍和史占中基于灰色马尔科夫模型对上海房价走势作了实证研究。［7］WangY.S.等开发了一个将统计方法，数据挖掘和人工智能结合在一起的集成预测方法，［8］闫妍等应用这个算法，对1998年一季度到2006年三季度的商品房销售价格指数进行了短期预测。［9］黄鹂用GARCH家族的模型对商品房销售价格指数做了预测分析。［10］陆金铸和陈红丽用Kalman滤波和AHP法对武汉的房价进行了预测。［11］王倩、王莹、邱继勤等基于灰色 GM（1，1）和BP神经网络对我国的平均房价作了预测。［12］纵观这些文献，可以发现两个特点。一个是，只采用一个模型，并且这个模型是事先预设的，因此不能确认所采用的模型是否是最佳模型，是否具有普遍性；另一个是，只就一个地区的房价指数和房价进行预测，而且这个地区也是随意选择的，或就全国平均房价和房价指数作预测，也不能判断得到的预测精度是否也具有普遍意义，因而缺乏全面性和完整性。

笔者以我国35个城市的同比房价指数和环比房价指数为考察对象，考察的目的在于通过对这些城市的同比和环比房价指数时间序列进行建模与预测，比较完整和全面地揭示我国房价指数的客观属性，即可预测性以及所适合的预测模型。鉴于G.W.Crawford和M.C.Fratantoni的研究结果［4］，即在预测时，简单的ARIMA模型更为精确，我们提出了一个基于径向基函数网络及其广义信息量的判别时间序列是否服从线性模型的检验方法。利用这个方法，首先检验房价指数是否服从线性模型。如果房价指数时间序列服从线性模型，那么就采用ARIMA模型来建模；如果不服从线性模型，就用多层径向基函数网络来建模。采用多层径向基函数网络的理由是这种网络有很强的非线性函数的逼近能力，能高精度地预测非线性时间序列。［13-14］实际检验表明，83%的城市的房价指数时间序列都是线性的，只有17%的城市的数据显示非线性。而在线性模型中，绝大多数是AR模型，只有个别是ARMA模型。我们还将不服从线性模型的时间序列用线性模型进行建模和预测，并将预测误差同多层径向基函数网络模型的结果做比较，发现后者的误差远小于前者，这说明了多层径向基函数网络的有效性。

二、建模和预测

（一）检验时间序列是否服从线性模型的方法

为了更好地了解房价指数时间序列的特点，检验它是线性的还是非线性的十分重要，我们提出了基于RBF网络及其广义信息量的检验方法，具体步骤如下：

1.用AR模型、ARMA模型和ARIMA模型对时间序列y1，y2，…，yN进行建模，得到最佳线性模型和对应的拟合残差时间序列e1，e2，…，eN。

2.对残差时间序列用不带线性项的单层RBF网络进行建模得到最佳网络，记其广义信息量为GIC1。记网络在令其权重为零时的广义信息量为GIC0，这是网络不起作用时网络的广义信息量。［13］如果GIC1＜GIC0，则说明我们可以进一步用非线性模型去拟合残差时间序列，原时间序列为非线性的。如果GIC1≥GIC0，则说明该残差时间序列不能再用非线性模型去拟合，于是就认为原时间序列是线性的，原来的线性模型就是最佳模型。在实际数据处理中，如果（GIC0-GIC1）/｜GIC0｜≤ε，就认为模型是非线性的。

（二）建模方法

采用AR模型、ARMA模型、ARIMA模型以及带线性项和不带线性项的多层径向基函数网络作为房价指数的候选模型，从中选择最适合的房价指数模型。具体建模步骤如下：

1.用AR模型、ARMA模型和ARIMA模型对房价指数时间序列y1，y2，…，yN进行建模，根据AIC的值选择最佳线性模型，并计算拟合残差时间序列e1，e2，…，eN。

2.检验房价指数时间序列是线性的还是非线性的。本研究取ε＝0.01。如果是线性的，那么第1步所得到的模型就是该时间序列的最佳模型，建模结束。如果是非线性的，则进入步骤3。

3.先分别用不带线性项和带线性项的单层RBF网络对时间序列进行建模，分别得到它们的最佳网络，并计算它们的广义信息量GIC。如果不带线性项的网络的GIC小于带线性项的GIC就建立纯非线性多层RBF网络，其模型的数学表达式为：

这是一个纯非线性模型。如果相反，就建立第一层带线性项的多层RBF网络，其模型的数学表达式为：

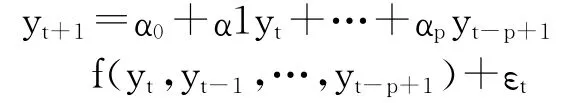
这是一个线性和非线性的混合模型。网络得到后，建模过程结束。

从上面的建模过程可以看到，本研究是在线性模型、非线性模型、线性和非线性的混合模型中挑选最合适的模型。而这些模型几乎涵盖了所有的定常时间序列模型，所以可以认为这个做法是恰当的。

需要说明的是，步骤2和步骤3中的每层RBF网络的中心和宽度都用采用浮点小数编码的自适应遗传算法得到，而权重都用正则最小二乘法得到，［14］适应度采用广义信息量GIC的倒数，这样得到的网络更具有泛化能力和良好的预测性能。此外多层RBF网络中各层的延迟步数取为第一层网络的延迟步数。

（三）数据和建模结果

我们采用了我国35个城市（见表1）从2005年8月到2012年12月的月度的同比和环比房价指数数据。将2005年8月到2012年9月的数据用于建模。用得到的模型对2012年10月、11月和12月进行动态预测。而2012年10月到2012年12月的实际数据用于检验预测精度。建模时对数据进行了归一化处理（见表1）。

同比房价指数时间序列线性和非线性检验结果显示：长沙、贵阳、合肥、济南、青岛、郑州这6个城市是非线性模型，占17%，其余29个城市都是线性模型，共占83%。环比房价指数时间序列线性非线性检验结果显示：长春、长沙、兰州、青岛、太原、武汉这6个城市是非线性的，占17%，其它29个城市是线性的，占83%。

需要指出的是，G.W.Crawford和M.C.Fratantoni，是首先将线性模型和非线性模型的预测值和实际值相比较，计算其均方根误差，由均方根误差的大小确定时间序列是线性的还是非线性的。所以在建模前是不知道房价指数时间序列是否服从线性模型。我们提出的检验方法恰好可以弥补这个缺点。

完成上述检验后，我们对房价指数时间序列进行建模，得到最佳模型。表1中列出了最佳模型，其中，LMRBF（p，m）表示第一层带线性项的多层RBF网络，PMRBF（p，m）表示纯非线性多层RBF网络，其中p为延迟步数，m为层数；此外“预测相对误差”按如下公式计算：

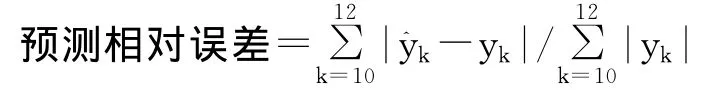
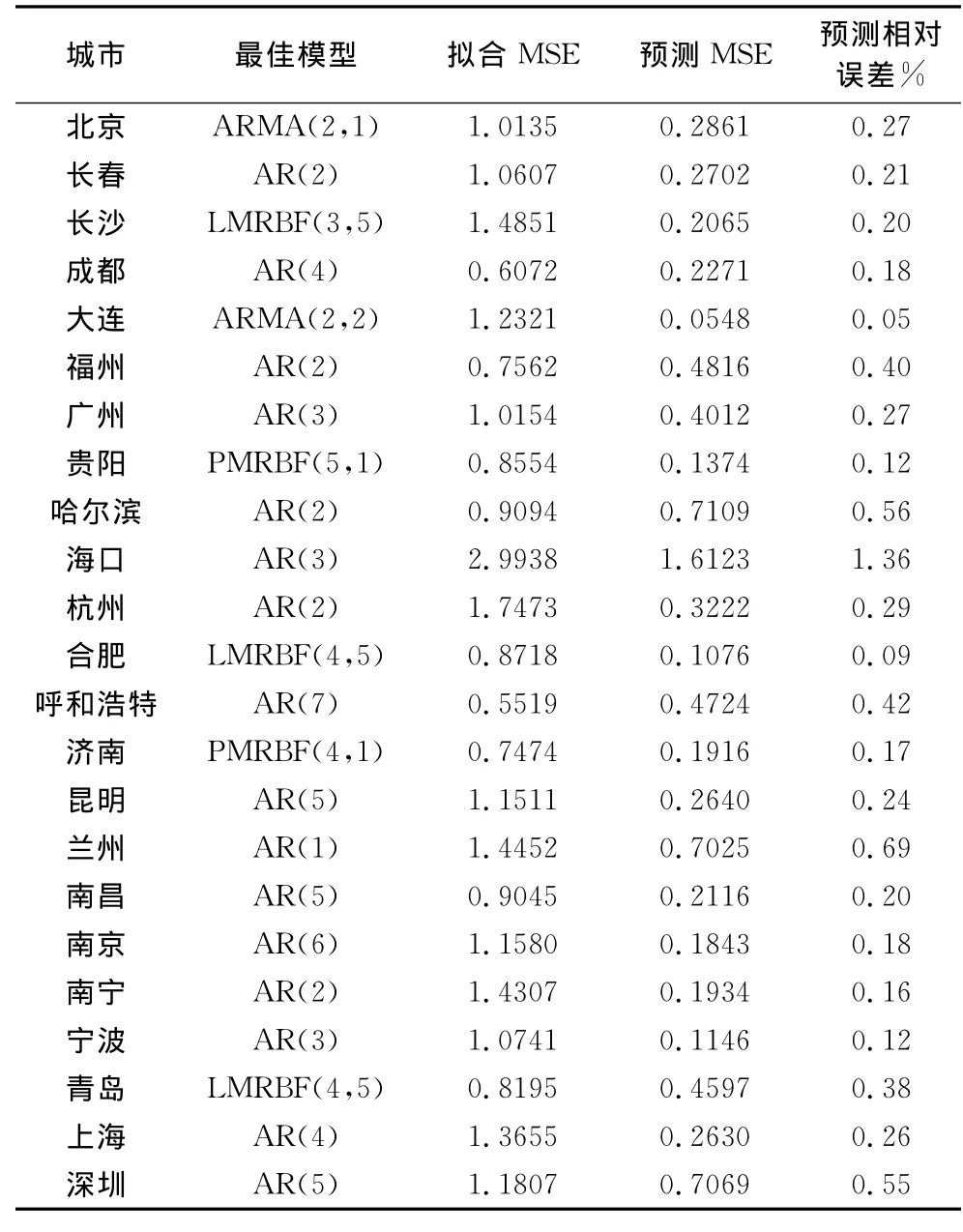
表1 同比房价指数建模和预测结果

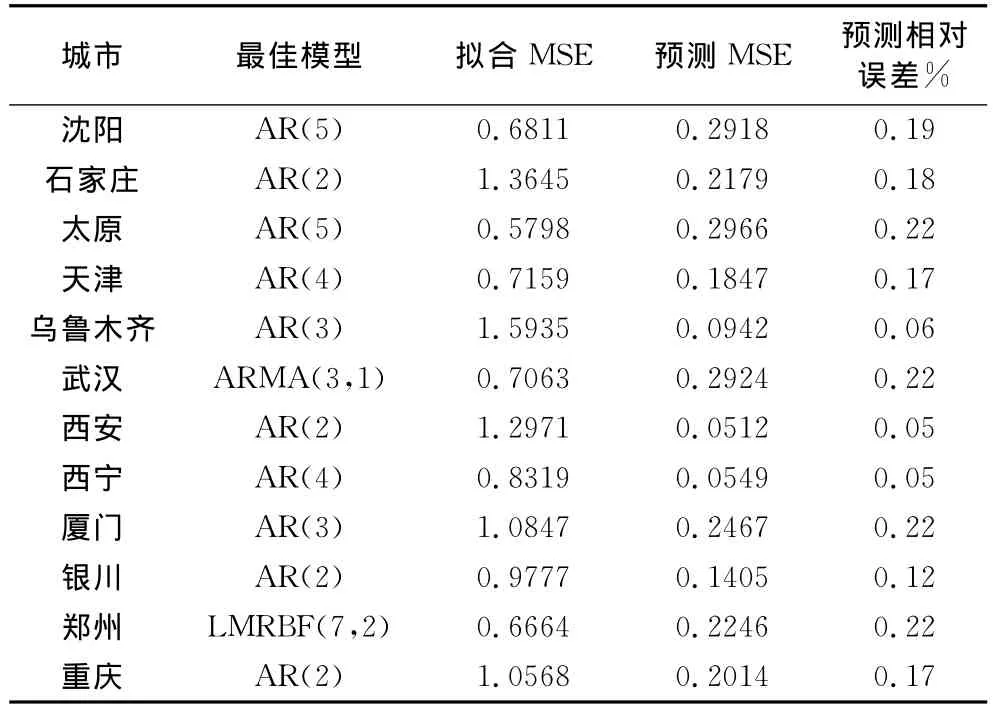
续上表

由表1可知，对同比数据，29个线性模型中，26个是最简单的AR模型，3个是ARMA模型。

对于环比数据（图表类似同比数据，限于篇幅限制，不在赘述），29个线性模型中，28个是最简单的AR模型，只有1个是ARMA模型。

以广州、上海两个城市为例。图1到图4列出了广州、上海两个城市的房价指数同比时间序列的拟合结果与预测结果。由这些图可以看到，拟合曲线和预测曲线在变化趋势上和实际数据是一致的，并且拟合和预测的精度大都较高。

此外，我们还对同比和环比时间序列的模型为非线性的序列进行了线性建模。同比数据的建模结果列在表2中，环比数据的建模结果列在表3中。为了便于比较，在表中列出了相应的非线性模型的结果。

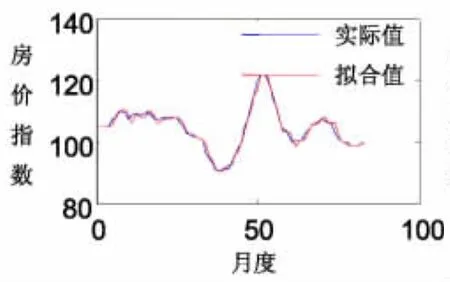
图1 广州同比房价指数拟合图

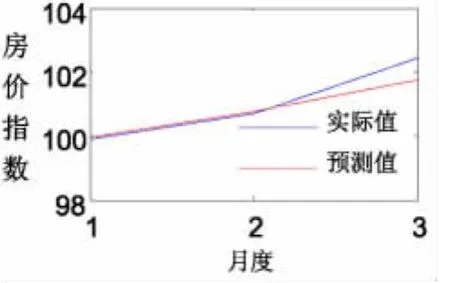
图2 广州同比房价指数预测图

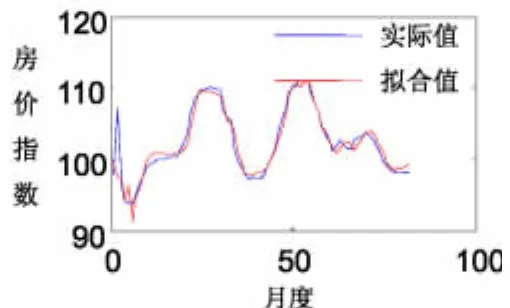
图3 上海同比房价指数拟合图

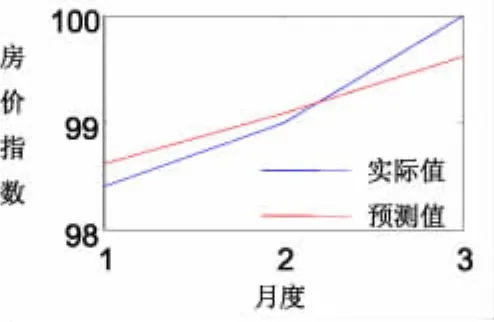
图4 上海同比房价指数预测图

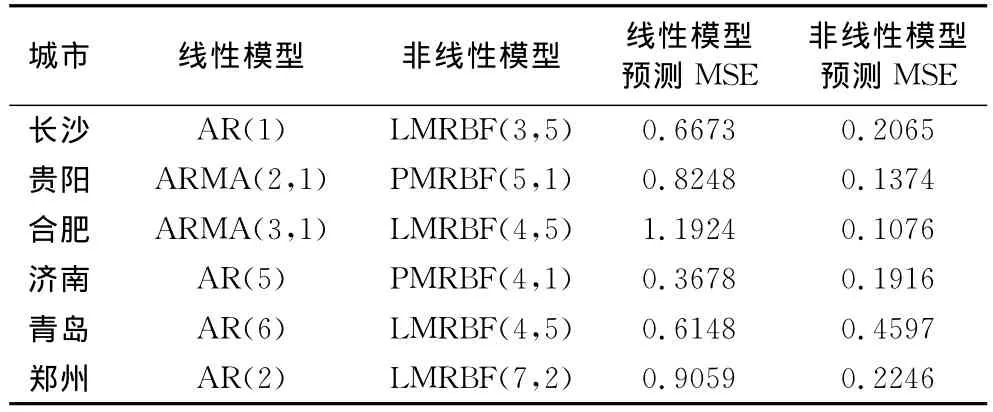
表2 同比时间序列的线性模型和非线性模型的预测误差比较

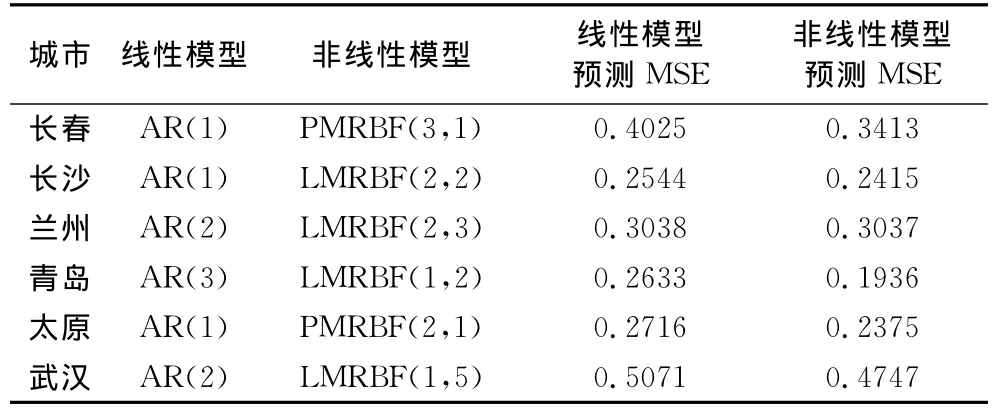
表3 环比时间序列的线性模型和非线性模型的预测误差比较

从表2可知，非线性模型的预测精度远高于线性模型。这说明对非线性同比时间序列，引入多层径向基函数网络是很有必要的。但从表3知，非线性模型的预测精度相比线性模型改善得不多。这说明同比房价指数非线性较强，环比房价指数非线性较弱。

四、结论

总结本文的研究结果，我们得到四个结论。（1）我国房价指数是可预测的。（2）我国房价指数的大部分模型都是线性模型，并且是简单的AR模型和ARMA模型。（3）房产价格指数的同比预测精度较高，环比的精度相对较差。（4）对不服从线性模型的房价指数，采用多层RBF网络可以大幅度提高预测精度。

［1］Case，K.and Shiller，R.The Efficiency of the Market for Single-Family Homes［J］.AmericanEconomicReview，1989，79（1）：125-137.

［2］Muellbauer，J.Murphy，A.Booms and Busts in the U.K.Housing Market［J］.EconomicJournal，1997，107（445）：1701-1727.

［3］Ortalo-Magne，F.，Rady，S..Housing Market Dynamics：On the Contribution of Income Shocks and Credit Constraints［R］.DiscussionPaper470，CESIfo.2001.

［4］Crawford，G.W.and Fratantoni，M.C.，Assessing the Forecasting Performance of Regime-Switching，ARIMA and GARCH Models of House Prices［J］.RealEstateEconomic，2003，V31（2）：223-243.

［5］王婧，田澎.小波神经网络在房地产价格指数预测中的应用［J］.计算仿真，2005，22（7）：96-98.

［6］杨楠，邢力聪.灰色马尔可夫模型在房价指数预测中的应用［J］.统计与信息论坛，2006，21（5）：52-55.

［7］谈萍，史占中.基于灰色-马尔可夫模型的上海房价走势实证研究［J］.科学技术与工程，2011，11（3）：661-663.

［8］Wang Y.S，Yu L，Lai KK.Crude oil price forecasting with TEI＠I methodology［J］.JournalofSystemsScienceand Complexity，2005，18（2）：145-166.

［9］闫妍，许伟，部慧，等.基于TEI＠I方法论的房价预测方法［J］，系统工程理论与实践，2007（7）：1-9.

［10］黄鹂.我国房屋销售价格指数AR模型的预测分析［J］，统计与决策，2013（7）：75-78.

［11］陆金铸，陈红丽.基于Kalman滤波法与AHP法的房价预测模型-以武汉市为例［J］，科协论坛，2007（12下）：54-55.

［12］王倩，王莹，邱继勤.基于灰色 GM（1，1）和BP神经网络的房价预测［J］，时代金融，2011（12下）：332-233.

［13］Zhuang，Jian，Jiang，Hai-Feng，Wu，Rui-Liu.Multi Layer RBF Network for Real Functions Approximation and nonlinear regression［C］//The2011InternationalConferenceonComputationalIntelligenceandSoftwareEngineering，2011.

［14］盛飞.多层径向基函数网络的自适应遗传算法［D］.马鞍山：安徽工业大学，2013.