A Periodic Single Species Model with Dissymmetric Bidirectional Impulse diffusion between Two Patches∗

LI Hong-li,ZHANG Long,WAN Hai-yun

(College of Mathematics and System Sciences,Xinjiang University,Urumqi,Xinjiang 830046,China)

Abstract: We consider a periodic single species model with impulse diffusion between two patches.By using the comparisontheoremofimpulsivedifferentialequationandsomeanalysismethods,weobtainsomesufficientconditionson the permanence of the system.Furthermore,by using Brouwer fixed point theorem and constructing a suitable Lyapunov function,some sufficient conditions on the existence and global asymptotic stability of unique positive periodic solution are established.

Key words:Dissymmetric impulse dispersal;Permanence;Periodic solution;Global asymptotic stability

0 Introduction

In recent years there has been a growing interest in the study of mathematical models of populations dispersing among patches in a heterogenous environment[1∼6].They obtained some sufficient conditions that guarantee permanence of population or stability of positive equilibria or positive periodic solutions.However,in all of above population dispersing systems,the authors always assume that the dispersal occurs at every time.In practice,it is often the case that diffusion occurs at certain moment.For example,when winter comes,birds will migrate between patches in search for a better environment,whereas they do not diffuse in other seasons,and the excursion of foliage seeds occurs at certain moment every year.Therefore,it is not reasonable to characterize the population movements in these cases with continuous dispersal models.This short-time scale dispersal is more appropriately assumed to be in the form of impulses in the modeling process,in order to be in much better agreement with the real ecological situation.With the developments and applications of impulsive differential equations,theories of impulsive differential equations have been introduced into population dynamics,and many important studies have been performed.Stability and permanence were considered by[7∼9].Existence of periodic solutions were studied by[10,11].

Hui and Chen[10]proposed the following single species logistic model with impulse dispersal:

where the authors suppose that the system(1)is composed of two patches connected by diffusion,xi(i=1,2)is the density of species in theith patch,ai,bi(i=1,2)are the intrinsic growth and density-dependent parameters of the population in theithpatch,diis the dispersal rate between theithpatch andjthpatch(ij,i,j=1,2).∆xi=xi(nτ+)−xi(nτ),wherexi(nτ+)represents the density of the population in theithpatch immediately after thenthdiffusion pulse at timet=nτ,xi(nτ)represents the density of the population in theithpatch before thenthdiffusion pulse at timet=nτ,n=1,2,···,i=1,2.

However,in the above impulsive dispersal models,it is assumed that the dispersal occurs between homogeneous habitat patches and the dispersal rate between any two patches is equal or symmetrical,which is really too idealized for a real ecosystem.Actually,in the real world,due to the heterogeneity of the spatio-temporal distributions in nature,movement between fragments of patches is usually not the same rate in both directions.In addition,once the individuals leave their present habitat,they may not successfully reach a new one,due to predation,harvesting,or for other reasons,so that there are traveling losses.Therefore,the dispersal rates among these patches are not always the same.Rather,in real ecological situations,they are different[12,13].Therefore,it is our basic goal to investigate single species model with dissymmetric impulse dispersal.

Besides,the coefficients of system(1)are assumed to be constant.However,in the real world,the coefficients are not fixed constants owing to the periodic variation of environment.The effects of a periodically varying environment are important for evolutionary theory as the selective forces on systems in a fluctuating environment differ from those in a stable environment.Thus,it is reasonable to assume that coefficients of system(1)are periodic functions.The effects of the periodic environment on the evolutionary theory have been the object of intensive analysis by numerous authors and some of these results can be found[14∼16].However,to the best of authors knowledge,there is no published paper considering the notion of a periodic single species logistic model with dissymmetric impulse dispersal in two patches.Therefore,it is worthwhile investigating the permanence of the species,existence,uniqueness,and global asymptotic stability of positive periodic solutions of system.

Based on the above considerations,in this paper,we consider the following periodic single species model with dissymmetric impulse dispersal between two patches.

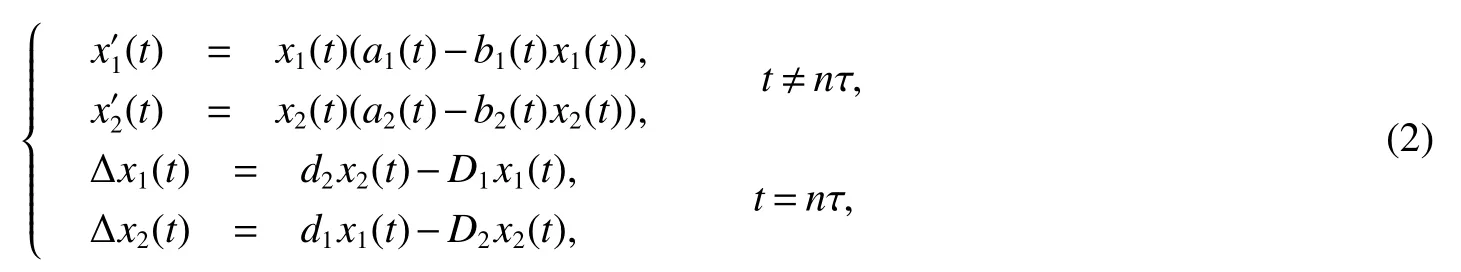
where we suppose that the system(2)is composed of two patches connected by diffusion,xi(i=1,2)is the density of species in theith patch,Di(i=1,2)is the rate of populationxiemigrating fromith patch,anddi(i=1,2)is the rate of populationxiimmigrating fromith patch.Here we assume 0≤di≤Di≤1,which means that there possibly exists mortality during migration between two patches.ai(t)andbi(t)(i=1,2)are τ-periodically continuous,andbi(t)>0(i=1,2)for allt∈R.

This paper is organized as follows.In section 1,we will give some notations and some lemmas.In section 2,some conditions for the permanence of the system(2)are obtained,we establish some conditions for the existence and global asymptotic stability of unique positive periodic solution of the system.

1 Preliminaries

In this section,we introduce some notations,and state some lemmas which will be useful in the subsequent sections.

LetPCandPC0denote two function spaces withPC={φ:[0,+∞)→Ris continuous fort,τk,φ()exist with φ(=limt→τ+kφ(t),k=1,2,···}andPC0={φ ∈PC:φ is differentiable attτk,k=1,2,···}.

Lemma 1[17]Let the functionx(t)∈PC0([t0,∞),R)satisfy the inequalities

wherea(t),b(t)∈PC([t0,∞),R)and αk≥0,βkare constants.Then

similarly,we obtain

for allt≥t0,if all the inequalities of(3)are inverse.

Consider the following nonlinear impulsive system:

wherea(t)andb(t)are bounded and continuous periodic functions de fined onR+,b(t)≥0 for allt∈R+and impulsive coefficients θk∈ (0,1),θk= θk+qandqis a fixed positive integer,andtk+q=tk+1.

Lemma2[18]Thereexistsauniquenonnegativeperiodicsolutionofsystem(4),whichisgloballyasymptotically stable.

Moreover,if

thenx∗(t)>0,if

thenx∗(t)=0.

2 Main results

In this section,we will study the existence and global asymptotic stability of positive periodic solution of species for system(2).

First,we discuss the permanence of the solutions of system(2).Throughout,letX=(x1,x2)≥0 forx1≥0 andx2≥0 and letX=(x1,x2)>0 forx1>0 andx2>0.Note that any solutionX(t)=(x1(t),x2(t))satis fiesX(t)≥0 for allt≥0 if the initial valueX(0)≥0.

Theorem 1We assume that

hold,then system(2)is permanent.

ProofFirst,we prove that the solutions of system(2)are ultimately bounded above.Let(x1(t),x2(t))be any solution of system(2)with initial valueX(0)>0,W(t)=x1(t)+x2(t),whent,nτ,we have

whereM=whent=nτ,we have

From(Theorem 3.11 of[19]),fort∈(nτ,(n+1)τ],we have

whent→∞,soW(t)is uniformly bounded.Hence,by the de finition ofW(t),there exist constantsM1>0,M2>0 such thatx1(t)≤M1,x2(t)≤M2fortlarge enough.

Finally,we prove that all the positive solutions of system(2)are ultimately bounded below.Sinced1≥0,d2≥0,we have

Little Thumb was not so much frightened as his brothers,30 and told them that they should run away immediately toward home while the Ogre was asleep so soundly, and that they should not be in any pain about him

In this system,we can see that there is no relation betweenx1(t)andx2(t).Thus,we can solve them independently.

Consider the impulsive comparison system of system(7)

If(5)holds,from Lemma 2,we obtain that(9)has a positive periodic solution(t),which is globally asymptotically stable,in view of Lemma 1,for any constant?>0 small enough,there is aT1>0 such that

for allt≥T1.A similar argument as in the proof of(10),for the above?>0 small enough,there exists aT2>0 such that

for allt≥T2.This completes the proof of Theorem 1.

Base on the discussion above mentioned,we know the set Ω =M2}is strictly positively invariant if conditions(5)and(6)hold.

Now,we will discuss the existence of positive periodic solution of system(2).LetX(t,X0)be unique solution of system(2)with initial valueX0=(x1(0),x2(0)),whereX(0,X0)=X0.Since Ω is positively invariant set of system(2).Then we can de fine a poincare map:

Obviously,the fixed point of mapFis corresponding to the periodic solution of system(2).

Theorem 2Assume that periodic system(2)satis fies the conditions(5)and(6)of Theorem 1,then system(2)at least exists a strictly positive τ periodic solution.

ProofFrom Theorem 1,we can obtain that

is a bounded closed convex set,andFΩ⊂Ω.

According to the property of continuous dependence of solutions with respect to initial value,Fis continuous.Furthermore,by applying the Brouwer fixed point theorem,there at least exists a fixed point of mapFin Ω,homologous,system(2)at least exists a strictly positive τ-periodic solution.This completes the proof of Theorem 2.

Following,we will try to establish some conditions under which the τ-periodic solution((t),(t))is unique and globally asymptotically stable.

Theorem 3Assume that the conditions of Theorem 1 hold,and

then system(2)has a unique globally asymptotically stable positive τ-periodic solution.

ProofLet(x1(t),x2(t))be any solution of system(2),de fine the Lyapunov function as follows:

Whenτ,we have

whent=nτ,we have

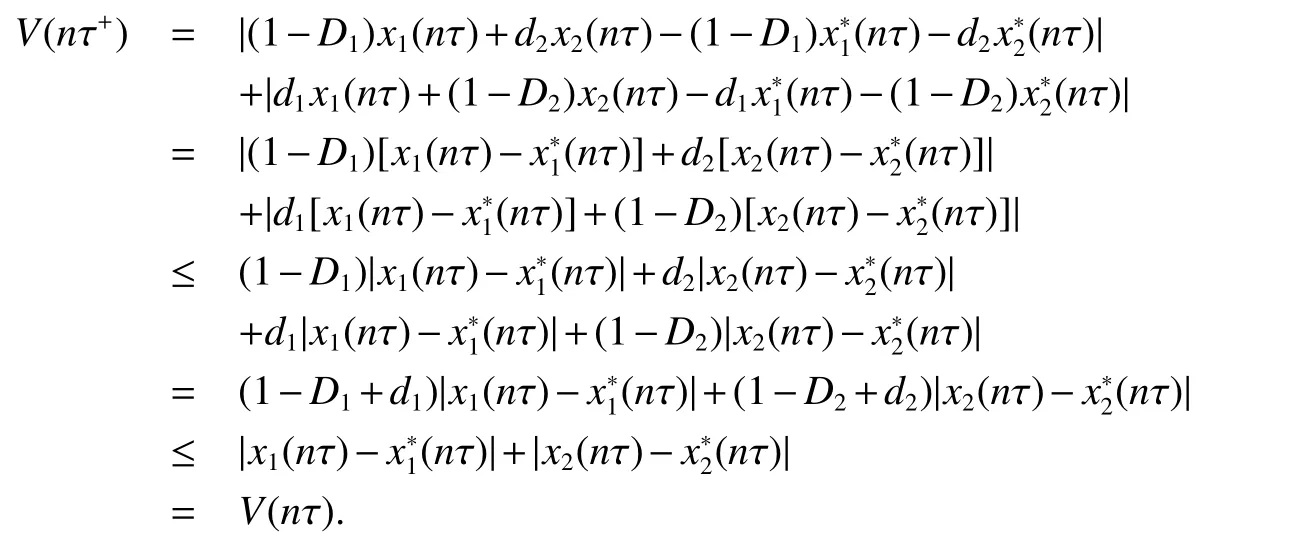
From(Theorem 3.11 of[19]),fort∈(nτ,(n+1)τ],we have

Hence,from(12)and(13),we haveSince the arbitrariness of the solution(x1(t),x2(t)),we finally obtain the uniqueness and the global asymptotic stability of the positive τ-periodic solution((t),(t)),this completes the proof of the Theorem 3.