Stochastic SIRS Epidemic Model with Generalized Nonlinear Incidence and Vaccination∗
Ramziya Rifhat,Xamxinur Abdurahman
(College of Mathematics and System Sciences,Xinjiang University,Urumqi,Xinjiang 830046,China)
Abstract: This paper deals with global dynamics of an SIRS epidemic model for infection with nonpermanent acquired immunity.The SIRS model studied here incorporates a preventive vaccination and generalized non-linear incidence rate as well as the disease-related death.The stochastic version,the global existence and positivity of the solution is showed,the global stability in probability and stochastically asymptotically stable in the large is proved under suitable condition on the intensity of the white noise perturbation.
Key words:Epidemic model;Lypunov function;Ito’s formula;Global stability in probability;Stochastic asymptotic stability;Almost sure exponential stability
0 Introduction
Quarantine and vaccination are commonly used in controlling and preventing the spread of diseases.Vaccination is considered to be the most successful intervention policy as well as a cost-effective strategy to reduce both the morbidity and mortality of individuals.It has been used to tackle diseases such as measles,mumps,rubella,diphtheria,tetanus,hepatitis B and in fluenza.However,vaccination does not necessarily imply life-long immunity for a vaccinated person.In some cases,vaccination is ineffective and fails to provide immunity at all,sometimes immunity acquired through vaccination wanes and does not provide life-long protection[1,2].Furthermore,it is practically impossible to vaccinate all susceptible individuals in a given community,especially in countries where such vaccines are not easily available or a ffordable.Hence,it is a task of great importance to determine a fraction of immune individuals in a population called the herd immunity threshold,above which a disease cannot become endemic[2].
To derive our model equations,we split the total population(denoted byN)into three compartments,the susceptible to disease,the infective and the recovered individuals with temporary immunity.The number in each class are denoted byS,I,andR,respectively.The rate at which new individuals enter the population isb,of which a fractionqis vaccinated,so the fraction(1−q)is susceptible with 0≤q≤1.The rate of natural death isµ.Infective individuals have an additional death rate due to the disease with rate constantc.The infective individuals recovered with rate α.We assume that that the transmission of the infection is governed by the incidenceabove hypotheses lead to the following model equations:
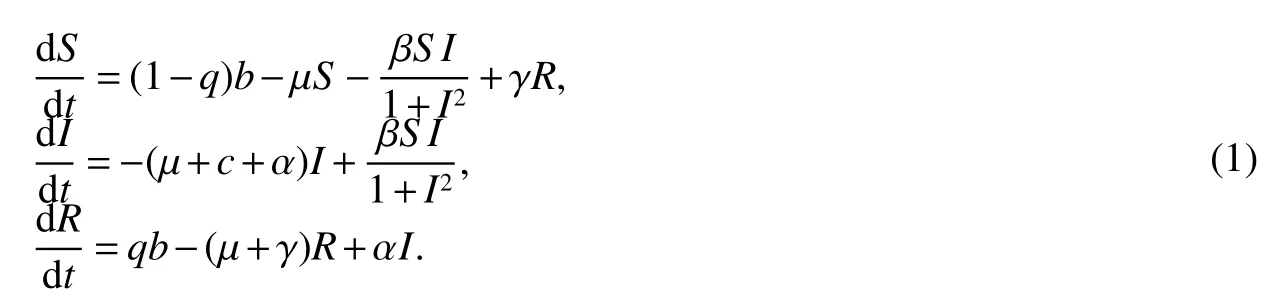
It is easy to show that system(1)is well-posed,in the sense that ifS(0),I(0)andR(0)are positive,then there exists a unique solution andS(t),I(t)andR(t)are positives for allt.
For the model(1),the basic reproduction number is
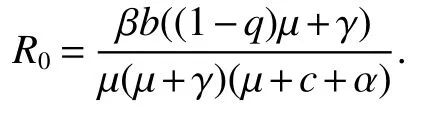
Set the right sides of(1)equal to zero,in the absence of infection(i.e.,I=0),the model has disease-free equilibrium state

And second one is the endemic equilibrium stateP∗
(i)IfR0≤1,then the disease-free equilibrium stateP0is global asymptotically stable.
(ii)IfR0>1,then the unique endemic equilibrium stateP∗is global asymptotically stable.
The proof of(i),(ii)can be found in[3].
In[4],global analysis of a deterministic and stochastic nonlinear SIRS epidemic model,where the incidence ratesa fractionqis vaccinated(q=0),in the paper mainly consider a stochastic version of the SIRS model by perturbing the deterministic system by a white noise.For the stochastic version,the global existence and positivity of the solution is showed,and the global stability in probability and pth moment of the system is proved under suitable conditions on the intensity of the white noise perturbation.
The next section will consider a stochastic version of the SIRS model where incidencea fractionqis vaccinated 0 whereS,IandRrepresent the number of susceptible,infective and recovered individuals,respectively,it should be positive.Moreover,in order for a stochastic differential equation to have a unique global solution for any given initial value,the coefficients of the equation are generally required to satisfy the linear growth conditions[5]that are not veri fied for our system.We must establish that the solution of system(2)is positive for allt≥0:This,will help us to study the global behavior of the solution of system(2)and to generalize the local results obtained in[6,7]by linearizing system(2)around the pointP0in the caseb=µanda=c=0. Throughout the rest of this paper,let(Ω;F;P)be a complete probability space with a filtration{Ft}t≥0satisfying the usual conditions(i.e.,it is increasing and right continuous whileF0contains all P-null sets).Let Theorem 1Let(S0,I0,R0)∈∆,then system(2)admits a unique solution(S(t),I(t),R(t))ont≥ 0,and this solution remain inwith probability 1. ProofLet(S0,I0,R0)∈∆,since the coefficients of system(2)are locally Lipschitz continuous,for any given initial value(S0,I0,R0)there is a unique local solution.The total population in system(2)veri fies the equation, Then,if(S(s),I(s),R(s))∈for all 0≤s≤talmost surely(brie fly a.s.),we get Hence,by integration we check ThenN(s),so Let?0>0 such thatS0,I0,R0>0,For≤0,considering stoping times where τeis explosion time.Consider functionV2de fined forX=(S,I,R)∈ <3+by Using Ito’s Formula,we have,for allt≥0,s∈[0,t∧τ] By(3),we assert thatS(s),I(s),R(s)∈It follows that wherek=By integration we obtain From(3),we haveV2(X(t∧τ))>0,thus where χAis the characteristic function ofA.Note that there is some component ofX(τ?)equal to?,we haveTherefore Combining(4)with(5)gives for allt≥0 Taking?to zero,we obtain for allt≥ 0,P(τ≤t)=0.Hence,P(τ= ∞)=1.Since τe≥ τ,we have τe= τ= ∞ a.s.This completes the proof. Consider the general n-dimensional stochastic system ont≥0 with initial valueX(0)=X0.The solution is denoted byX(t,X0).Assume thatf(t,0)=g(t,0)=0 for allt≥ 0,then origin pointX=0 is an equilibrium of system(6). De finition 1EquilibriumX=0 of system(6)is said to be: (i)almost surely exponentially stable if for allX0∈ (ii)stochastically stable in probability if for all?>0, (iii)stochastically asymptotically stable in the large if it is stochastically stable and,moreover for allx0∈Rd For more de finitions of stability for system(6)we refer to[8].We denote byLthe differential operator associated to system(6),de fined for a functionV(t,x)∈C1,2(<× Now we present the following theorem which gives conditions for the stochastic asymptotic stability of the equilibrium of the stochastic system(6)in terms of Lyapunov function(see[8]): Lemma 1If there exists a positive-de finite decrescent radially unbounded functionV(x,t)∈C1,2(Rd×[t0,∞);R+)such thatLV(x,t)is negative-de finite,then the trivial solution of system(6)is stochastically asymptotically stable in the large. Theorem 2then disease-free equilibriumP0of system(2)is stochastically asymptotically stable in the large. ProofConsidering Lyapunov function wherex=(S,I,R),we have and as0,thenV3(x)>0.HenceV(x)is positive-de finite decrescent radially unbounded. we obtain that which can be simpli fied to Lemma 2[10](Strong law of large numbers)LetM={Mt}t≥0be a real-valued continuous local martingale vanishing att=0.Then Theorem 3disease-free equilibriumP0is almost sure exponential stability in∆. ProofLet(S0,I0,R0)∈∆.In virtue of Theorem 1,the solution of system(2)remains in∆.Then,we de fine function With the application of the multi-dimensional Ito’s formula(see[9]),we obtain where dBdB=dtand dBdt=dtdB=0.Since dSdSand dRdR=dSdR=dIdR=0,we have, and by integration we get From Theorem 1,the quadratic variation of stochasticThus,from Lemma 2,the strong law of large number for local martingales[10]implies that Therefore,from(10)and(11),we conclude that This completes the proof. Concerning the stochastic model,we obtained sufficient conditions for stochastic stability of the disease-free equilibriumP0of system is stochastically asymptotically stable in the large and probability sense by using a suitable Lyapunov function and other technics of stochastic analysis.The investigation of this stochastic model revealed that the stochastic stability ofP0depends on the magnitude of the intensity of noise σ as well as the parameters involved within the model system.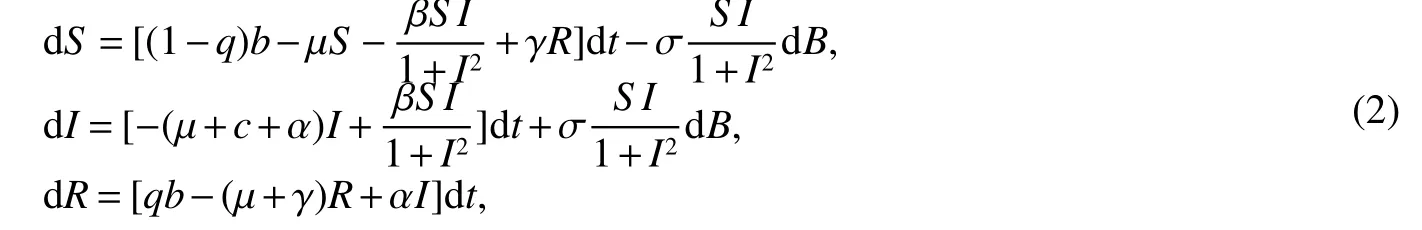
1 Global existence and positivity
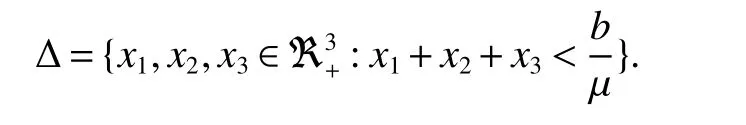
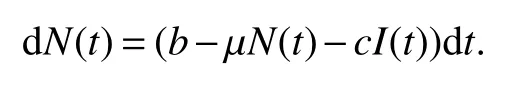
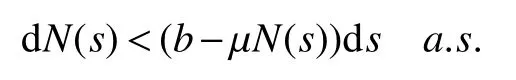
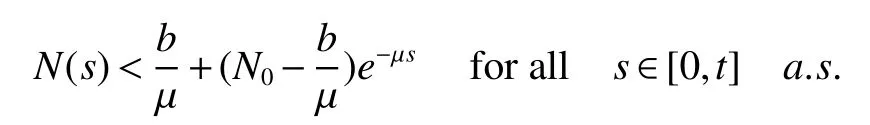

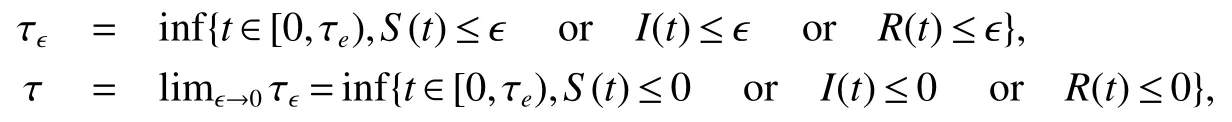

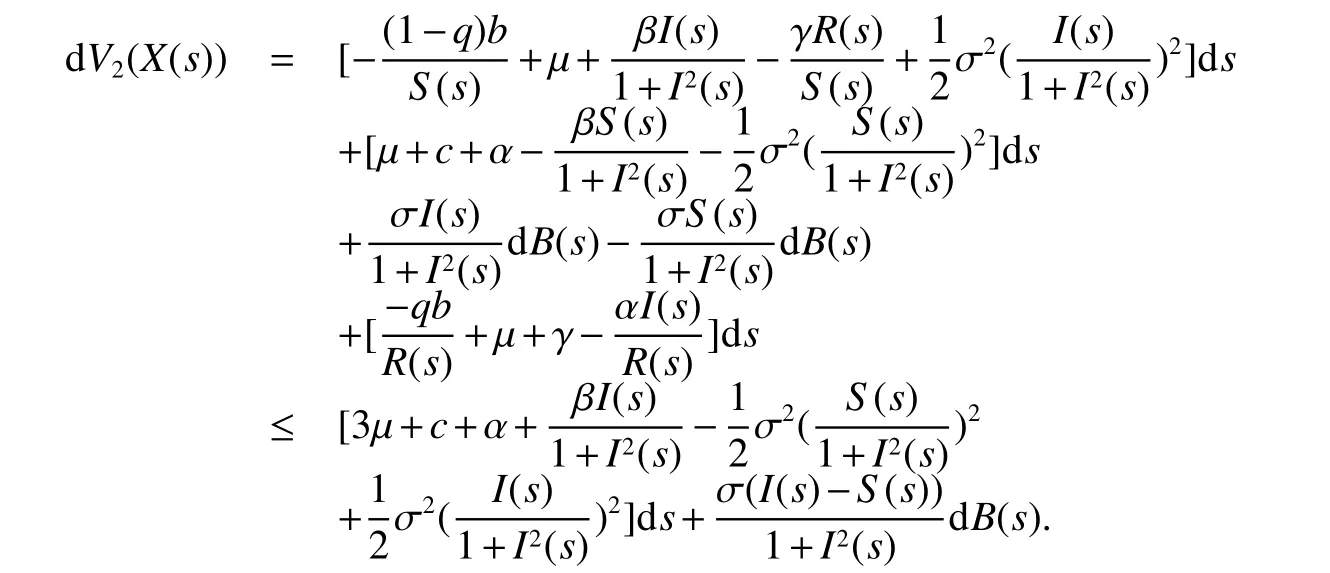
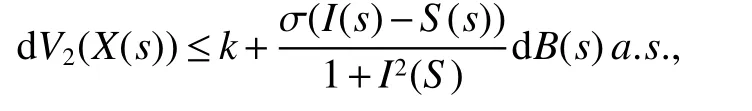
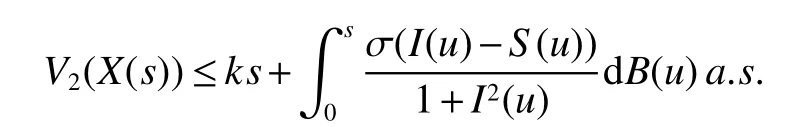

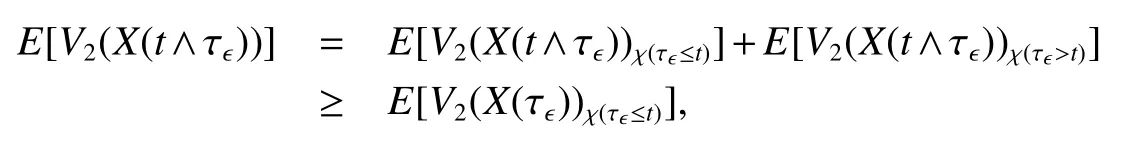
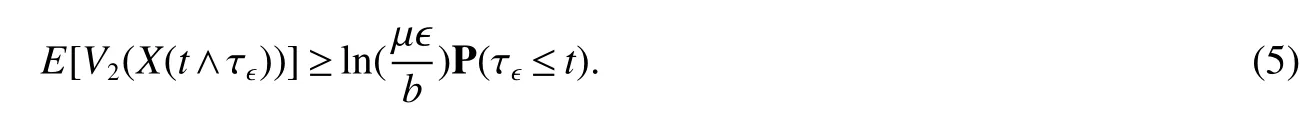

2 Global behavior

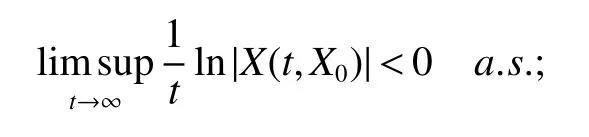
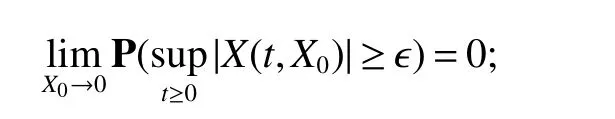
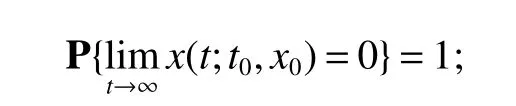
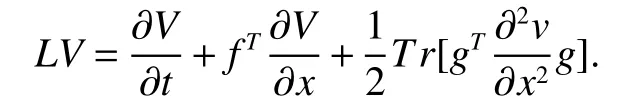
2.1 Stochastic asymptotic stability
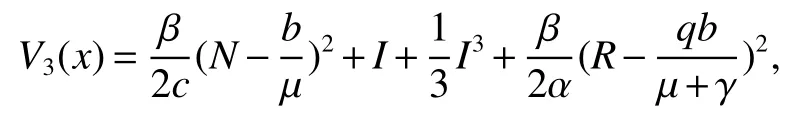
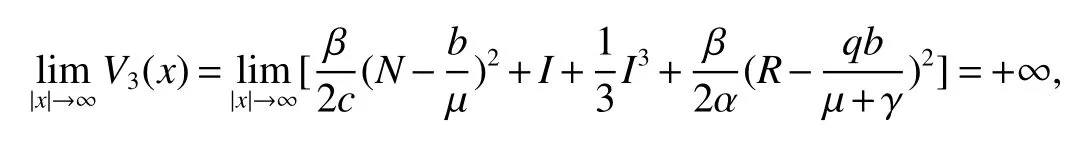
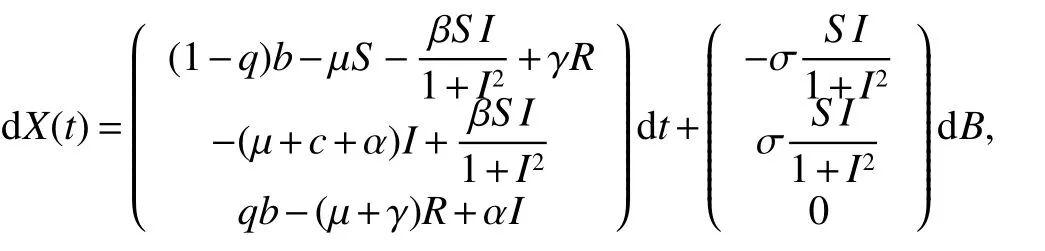
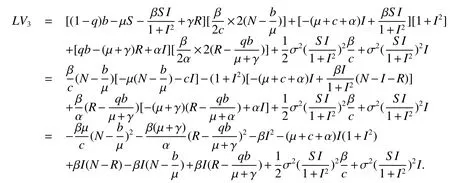


2.2 Almost sure exponential stability
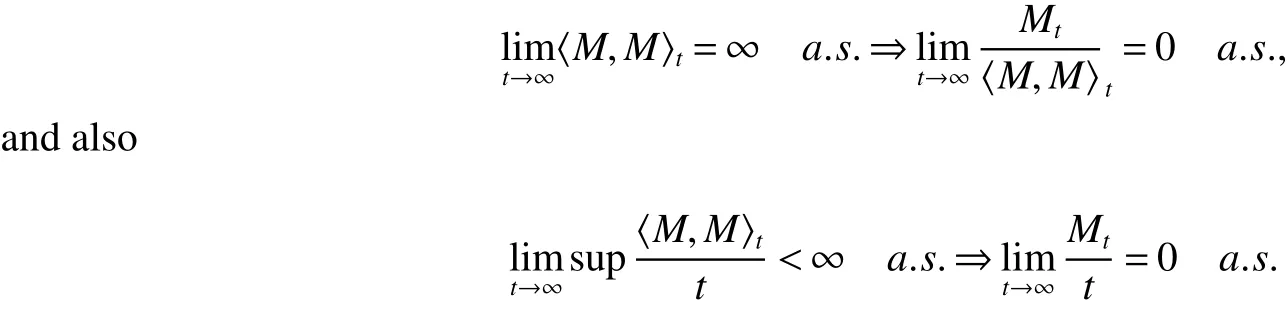
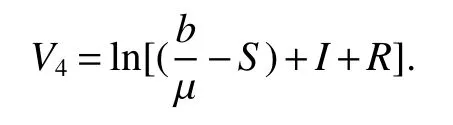
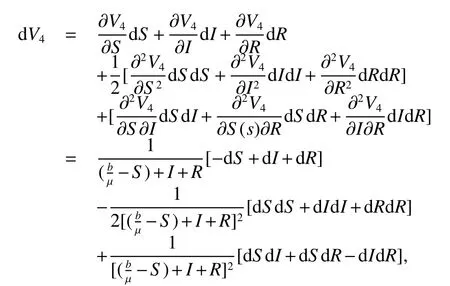

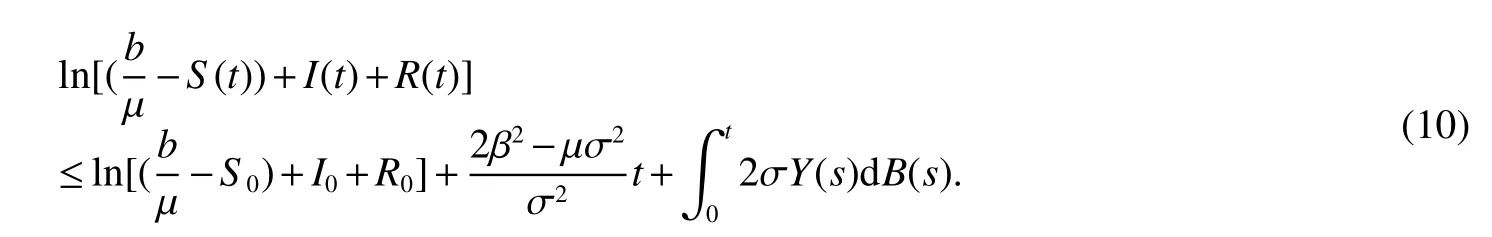


3 Conclusion

