Global Stability of Cellular Neural Networks with Pantograph Delays∗
CHEN Gang,JIANG Hai-jun,HU Cheng
(College of Mathematics and System Sciences,Xinjiang University,Urumqi,Xinjiang 830046,China)
Abstract: In this paper,we study the global stability of the equilibrium point for the cellular neural networks with pantograph delays under parameters uncertainties.By constructing a suitable Lyapunov functional,two new sufficient conditions are derived for the global asymptotic stability of the system.
Key words:Cellular neural network;pantograph delay;Global robust asymptotically stability
0 Introduction
Since L.O.Chua[1,2]put forward cellular neural network(CNNs)theory and since application.Because of its huge potential application,has become a new hot topic research.During the implementation of neural networks,time delays cannot be avoided during the processing and transmission of the signals.In practice,time delays are usually variable with time.Therefore consider delay of cellular neural network more meaningful.1990 by Rosha and Chua put forward time-delay cellular neural network(DCCNs).It has the characteristics of cellular neural network and expand the application fields.As in the CNNs and DCNNs applications usually need there is only one of the global network convergence equilibrium point.So equilibrium point research been concerned.About DCNNs stability of the equilibrium point.Many scholars have made a great deal of research.By often evolve into the situation with time-varying delay,distributed delays the and so on.In recent years,the study on stability of cellular neural networks with time delays has received considerable attention,and varieties of interesting results have been presented in the literatures,see[3∼28],constants delays[8∼10,21,28],time-varying delays[5,6,11,13,16,17,20,22,25∼27],distributed delays[12,14,21,23].
Nowadays,pantograph delays is playing more and more important part in some fields.For example pantograph delay is usually required in Web quality of service(QoS)routing decision.Pantograph delay systems also have important applications in some areas such as physics,biology systems and control theory.However,few authors has taken care of cellular neural networks with pantograph delays.Therefore,it is important and necessary to study the stability of cellular neural network with pantograph delays.
In this paper,we study the global asymptotic stability of the equilibrium point for the neural networks with pantograph delays.This paper proposes new results for the existence,uniqueness and global asymptotic stability of the equilibrium point for cellular neural networks with pantograph delays under parameter uncertainties.By using Lyapunov stability theorem and applying homeomorphism mapping theorem,new delay-independent stability criteria are obtained.The obtained results are in terms of network parameters of the neural system only and therefore they can be easily checked.
In rest of this paper is organized as follows:In section 2,we give the model description and preliminaries.In section 3,by using the homeomorphism mapping,we can obtained the existence and uniqueness results of the equilibrium point.In this section 4,we provide sufficient conditions for global robust asymptotically stability of the equilibrium point of the system 1.Finally,we give the conclusion in section 5.
1 Problem formulation and some preliminaries
In this section,we give some useful facts and results that are important in the context of the this paper.
We consider the following cellular neural network model with pantograph delays:

Whereciis the charging rate for the neuroni.xi(t)is the state vector associated with the neurons.aijandbijdenote the strengths of connectivity between neuronsjandiat timetandqjt,whereqjis constants.0 In order to completely characterize the parameter uncertainties,the quantitiesaijandbijandciin the neural network model(1)are assumed to satisfy the following parameter ranges: In this paper,the activation function is assumed to satisfy the following properties: (H1).fi(xi)(i=1,2,...,n)is bounded and monotonically nondecreasing onRand there exist positive constantlisuch that DenoteL=diag(l1.l2,...,ln),LM=max1≤i≤n(li). For a vectorx=(x1,x2,...,xn)T∈Rn,kxk2denotes the Euclidean norm de fined by(|x1|,|x2|,...,|xn|)Tdenotes the absolute-value vector.For matrixA=(aij)n×n,ATdenotes the transpose;A−1denotes the inverse; λmax(A)and λmin(A)denote the largest eigenvalue and the smallest eigenvalue ofA.|A|=(|aij|)n×ndenotes absolute value matrix.denotes the spectral norm ofA.Idenotes the identity matrix. De finition 1[4]The cellular neural network model(1)with the parameter ranges de fined by(2)is globally robust asymptotically stable,if the unique equilibrium pointx∗=(,,...,)Tof the cellular neural systems is globally asymptotically stable for allC∈CI,A∈AI,B∈BI. Lemma 1[10]Letx=(x1,x2,...,xn)T∈Rn.IfA∈AIthen,for any positive diagonal matrixP,the following inequality holds: Lemma 2[7]If the matrixBin(2)satis fiesB∈[B,B¯],then,the following inequality holds: Lemma 3[8]If the matrixBin(2)satis fiesthen,the following inequality holds: Lemma 4[9]If the matrixBin(2)satis fiesthen,the following inequality holds: Lemma 5[8]H(x):Rn→Rnis a homeomorphism ifH(x)satis fies the following conditions: (1)H(x)is injective, (2)H(x)is proper,i.e.,kH(x)k→+∞as kxk→+∞. In this section,we will derive an improved sufficient condition for the existence and uniqueness of the equilibrium point for cellular neural system(1).Furthermore,we analyze the global robust asymptotically stability of the equilibrium point: Theorem 1Let Assumption(H1)be satis fied,the system(1)has an unique equilibrium point,if there exist positive diagonal matricesP=diag(p1,p2,...,pn)andL=diag(l1,l2,...,ln),such that ProofFirst,we prove the uniqueness of the equilibrium point.we de fined the following mapping associated with(1). To complete the proof,it is sufficient to show thatH(x)is a homeomorphism onRn.For two vectorsx,y∈Rn,x,y,we can write Multiplying both sides of(4)by 2(x−y)TP,we have we know that The woman did everything exactly as she had been told. As soon as the full moon appeared she carried the golden spinning wheel to the bank, and span diligently24 until she was out of flax, and the spool was completely filled with thread. She had scarcely placed the wheel on the bank when there was a more violent motion than before from the water s depth. Then a powerful wave rushed up and carried the wheel away with it. From Lemma 1,we know that and Using(6)and(7)in(5)we can get We know that Λ>0,then Therefore,it directly thatH(x),H(y)for allx,y.i.e,H(x)is injective. From(8),lettingy=0,we have It follows that Since kH(0)k2is finite,it is obvious that kH(x)k2→+∞ as kxk2→+∞.i.e.,H(x)is proper.From Lemma 5,H(x)is a homeomorphism onRn.Which implies that system(1)has a unique equilibrium point We now proceed with the following results: Theorem 2Let Assumption(H1)be satis fied,the system(1)has an unique equilibrium point,if there exist positive diagonal matricesP=diag(p1,p2,...,pn)andL=diag(l1,l2,...,ln),such that whereS=(sij)n×nwith ProofWe know that the following inequalities hold: Using(7)and(9)in(5)we obtain Note that(10)is exactly in the same form as(8).Therefore,if Φ>0 then kH(x)k2→+∞as kxk2→+∞andfor all,implying the existence and uniqueness of the equilibrium point for the system(1). In this section,it will be shown that the conditions obtained in Theorem 1 and 2 also imply the global asymptotic stability of the equilibrium point system 1 under the parameter uncertainties given by(2). Using the transformationzi(t)=zi(t)−one can shift the equilibrium point for system(1)to the origin and put the system into the following form: Sincez→0 implies thatx→x∗,to prove the asymptotic stability ofx∗,it will be sufficient to prove the asymptotic stability of the origin of system(11). Theorem 3Let Assumption(H1)be satis fied,cellular neural network model(1)is globally robust asymptotically stable,if there exist positive diagonal matrixP=diag(l1,l2,...,ln),such that ProofTo prove the global robust asymptotically stability of neural system(1),we consider the following Lyapunov function: The time derivative ofV(t)along the trajectories of system(12)is obtained as we know that We know that Using(14)-(15)and(17)in(13),we have Therefore,under the given condition Λ>0,we haveV˙(y(t))<0,which implies that system(1)is global asymptotically stable.Thus,by De finition 1,system(1)is globally robust asymptotically stable. We now proceed with the following results: Theorem 4Let Assumption(H1)be satis fied,the system(1)is globally robust asymptotically stable,if there exist positive diagonal matrixP=diag(l1,l2,...,ln),such that ProofFrom(9),we can write Using(17)and(19)in(13),we can obtained Therefore,under the given condition Φ>0,we have˙V(z(t))<0,which implies that system(1)is global asymptotically stable.Thus,by De finition 1,system(1)is globally robust asymptotically stable. LettingP=pIbe a positive scalar matrix in Theorem 1,we can obtain the following LMI criterion: Corollary1LetAssumption(H1)besatis fied,neuralnetworkmodel(1)isgloballyrobustasymptoticallystable,if there exist positive constantsp,and positive diagonal matrixL=diag(l1,l2,...,ln),such that Remark 1In system(1),lettingqj=1,j=1,2,...,n.We can easily see that system(1)is the cellular neural network without time delays. Remark 2In system(1),lettingqjt=t−(1−qj)t,j=1,2,...,n.Then the system(1)can be transformed into the cellular neural network with time-varying delays. We have studied the global robust asymptotically stability of the equilibrium point of cellular neural networks with pantograph delays.We conduct a stability analysis by exploiting the stability theory of Lyapunov functionals and the theory of Homomorphic mapping to derive some easily veri fiable sufficient conditions for existence,uniqueness and global asymptotic stability of the equilibrium point.We present two improved sufficient conditions for the existence,uniqueness and global robust asymptotically stability of the equilibrium point for cellular neural networks with pantograph delays.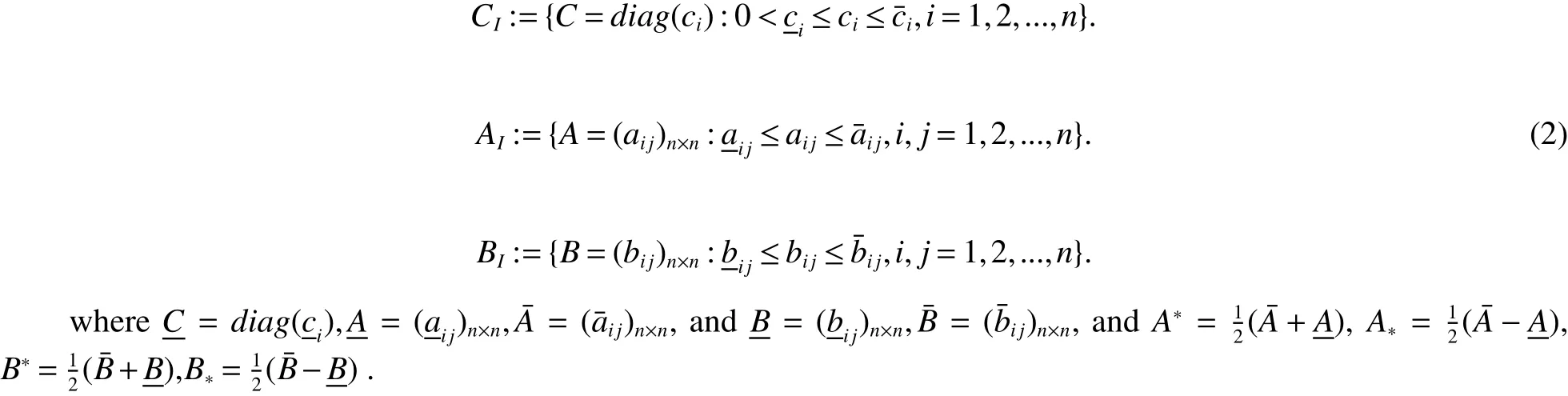

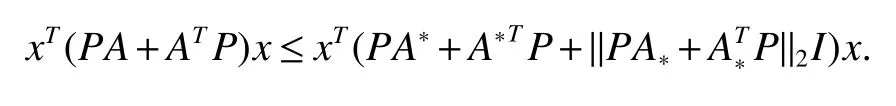



2 Existence and uniqueness analysis of equilibrium point











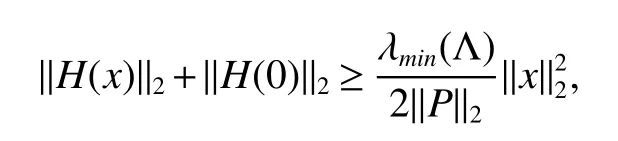



3 Stability analysis of equilibrium point
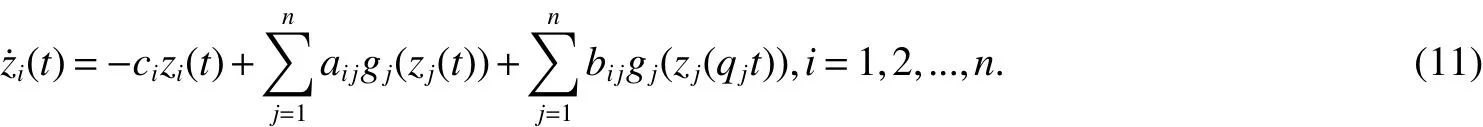
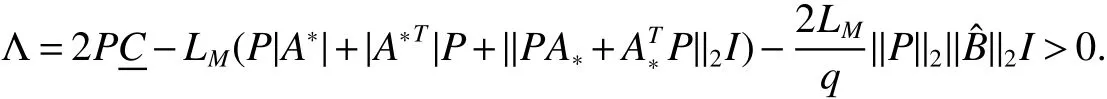

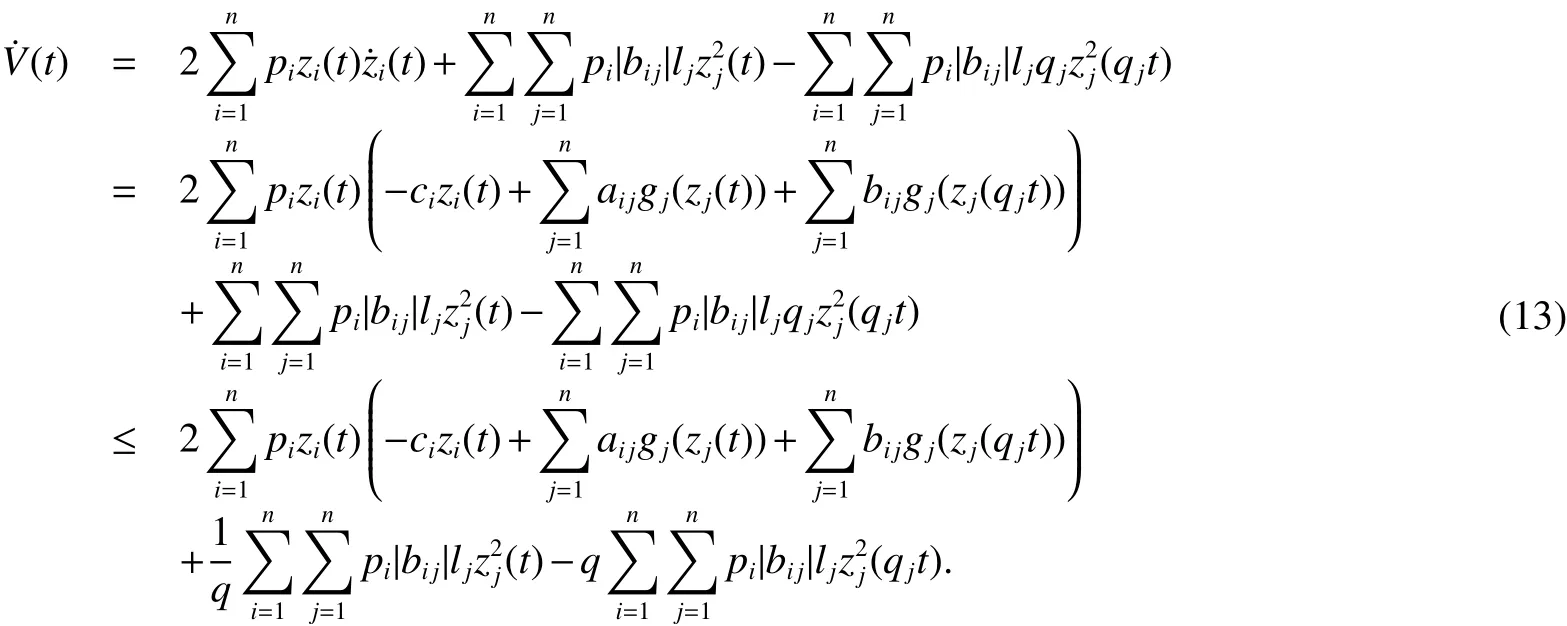

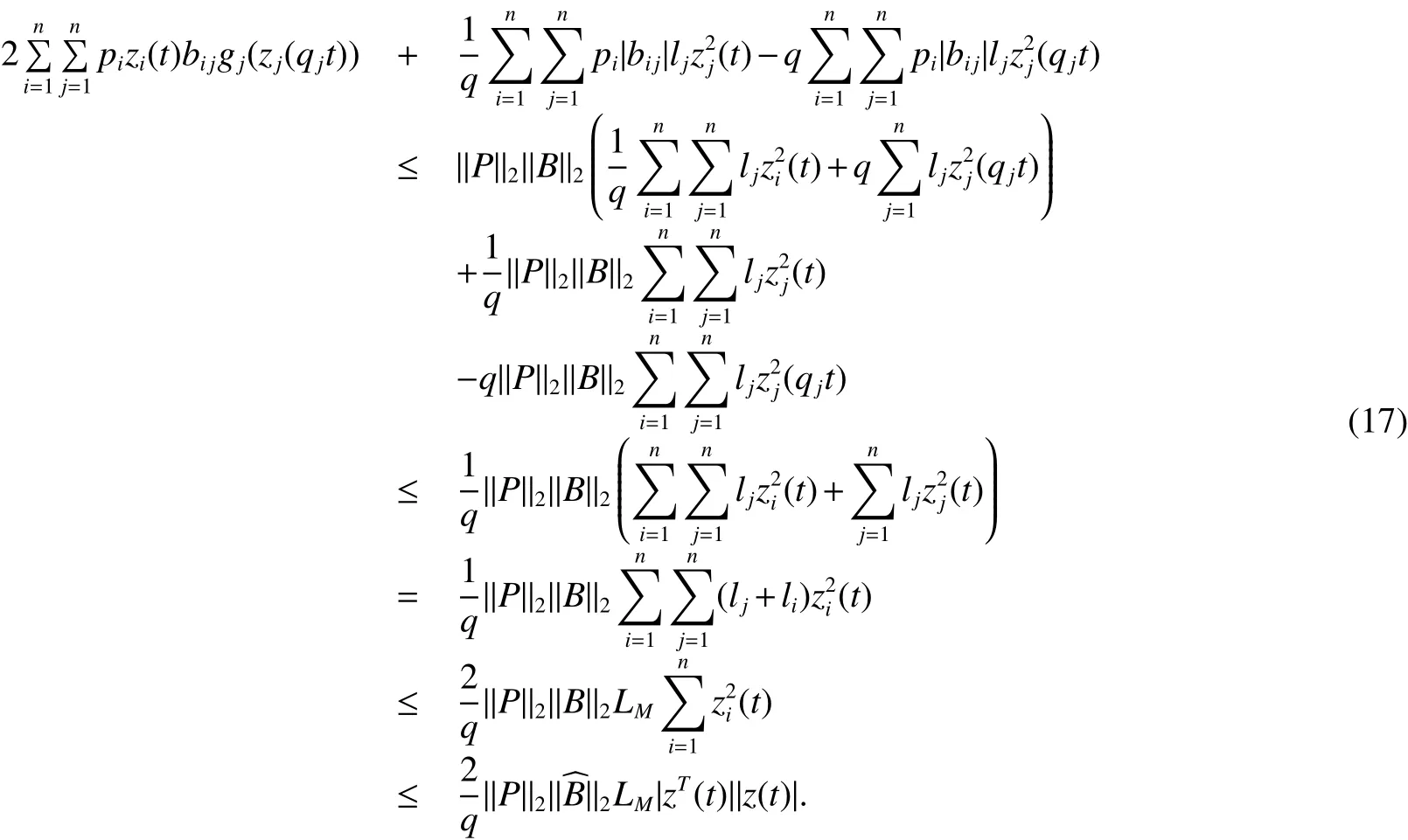
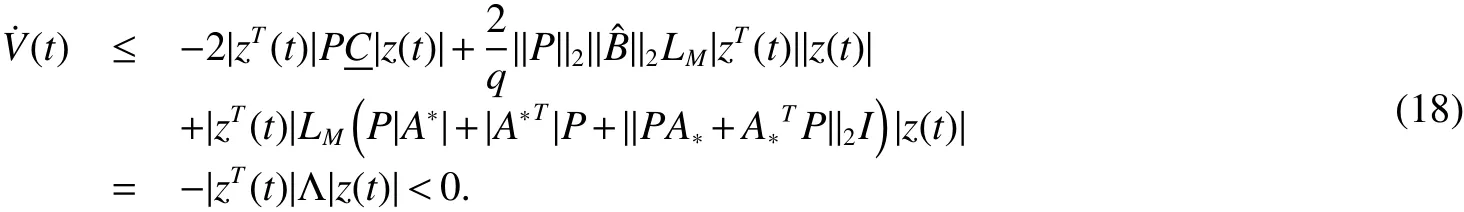


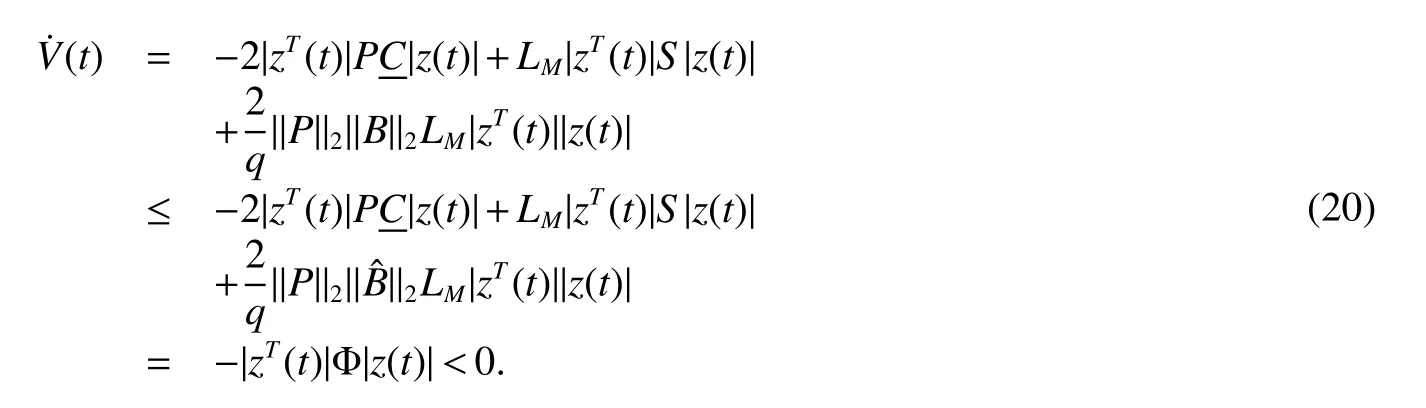

4 Conclusions
- 新疆大学学报(自然科学版)(中英文)的其它文章
- Arc Connectivity of Balanced Half-transitive Digraphs∗
- A Phosphoric Acid Pretreatment of Activated Carbon Supported Pd Catalyst for Acetylene Hydrochlorination∗
- Keyword Language Identi fication in Uighur,Kazakh,Kyrgyz and Chinese Multi-lingual Dictionary System∗
- 塔克拉玛干沙漠腹地克里雅河尾闾圆沙三角洲沙质沉积物粒度特征∗
- 新疆加曼特金矿与阿希金矿的流体包裹体特征对比研究∗
- On the Laplacian Integral of Tricyclic Graphs∗

