双三相感应电动机矢量控制调速系统建模与仿真

张 岳，沈建新

(浙江大学，杭州 310027)

0 引 言

近年来，随着电力电子技术的发展，多相电机驱动系统相比普通三相系统显示出了不少特有的优势，因而越来越广泛地被应用于需要高功率、高可靠运行的场合，如新能源汽车牵引、船舶推进等［1－3］。其中，作为一种常见的多相电机系统，双三相感应电动机具有两套对称的、空间位置互差30°电角度、中心点相互独立的三相星形连接定子绕组［4－5］，制造成本较低。研究表明这种双三相感应电动机不仅能够有效消除转矩脉动中的六次分量，同时也能够通过减少转子电流谐波分量来降低转子损耗［6］。双三相感应电动机系统还能够减少直流母线电流的谐波含量，提高整个系统的稳定性［7］。

针对双三相感应电动机调速系统的研究，目前的文献大多从产生多电平的角度介绍了双三相感应电动机驱动技术［8－9］;或者将电机模型在静止坐标系下进行变换，从而对双三相感应电动机进行控制［10－12］。上述方法虽然能够较好地控制双三相感应电动机的运行性能，但是存在计算模型及相应的控制策略复杂的问题。基于此，本文首先建立双三相感应电动机在静止坐标系下的模型;在此基础上针对该电机的绕组特点，推导了在同步旋转的正交坐标系下的数学模型，在这个旋转坐标系下双三相电机绕组能够实现高性能的解耦控制;研究双三相感应电动机转子磁场定向的矢量控制方法，并建立矢量调速系统的仿真模型。仿真结果表明，本文介绍的双三相感应电动机矢量控制系统具有优良的动态运行性能。

1 双三相感应电动机数学模型

1.1 原坐标系模型

(1)磁链模型

图1 双三相感应电动机定、转子绕组轴线矢量图

双三相感应电动机定、转子绕组轴线矢量关系如图1所示。其中定子绕组分别标记为A－B－C及U－V－W;转子绕组经归算后的等效绕组为a－b－c。则电机定子、转子间的自感和互感具有如下关系。

定子自感:

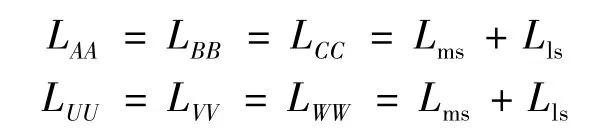
转子自感:

式中:Lms为励磁电感;Lls、Llr分别为定转子绕组漏感。定子绕组间电感(忽略定子绕组间互漏感):

定、转子间互感:

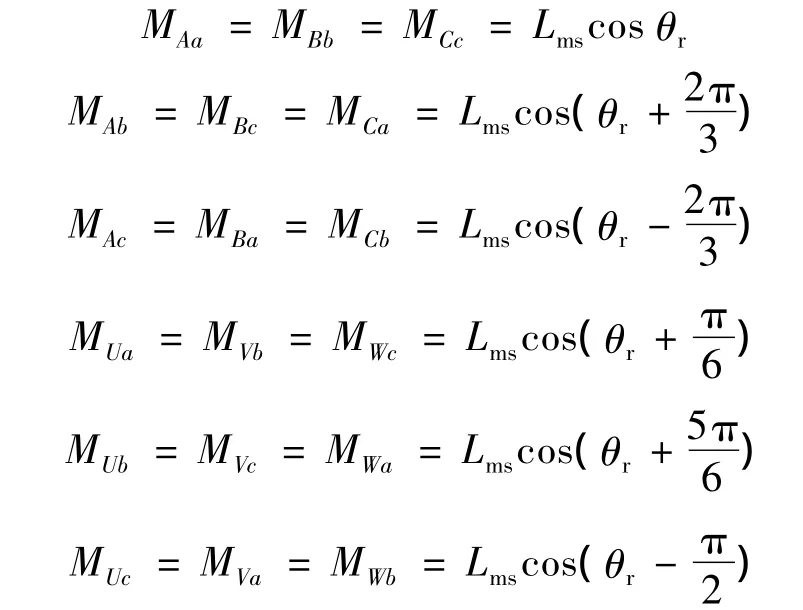
式中:θr为转子位置空间角度，即转子a相绕组与定子A相绕组轴线间的夹角;iA和iU分别为定子绕组A相与U相电流;ia为归算到定子边的转子a相电流，其余以此类推。由此可得电机磁链方程:

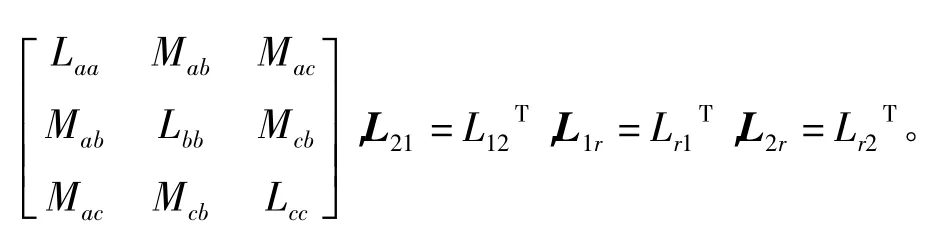
(2)电压方程

双三相感应电动机的电磁转矩为Te，由机电能量转换的原理，电机的电磁转矩等于机械角位移变化时磁共能的变化率，因此双三相感应电动机电磁转矩Te的表达式经整理后:

式中:p为电机极对数。

运动方程:

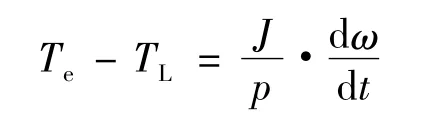
式中:TL为电机的负载与阻尼转矩之和;J为电机转动惯量;Ω为电机的机械转速。

式中:从以上推导的电机模型可以看到，双三相感应电动机是一种非线性、强耦合的系统。从电压方程、磁链方程中看到，不仅存在定子、转子之间的耦合，还存在定子绕组间的交叉耦合;转矩方程中包含状态变量之间的乘积项。这些系统复杂性与高度耦合性都给电机控制带来很大困难。

1.2 双三相感应电动机双dq坐标系下的模型

为了解决双三相电机的耦合问题，文献［10－12］通过一个坐标变换矩阵，将电机分解到三个二维的子坐标系统。考虑到双三相感应电动机的绕组是由两套相互独立的三相绕组构成的特点，可以采用三个三维的坐标变换矩阵，将两套定子绕组和一套转子绕组分别以不同的坐标变换矩阵变换到同一套以同步速旋转的d，q坐标系上，或者说变换后的第一套定子绕组的d轴、第二套定子绕组的d1轴与转子绕组的dr轴是重合的，都位于同步速旋转的d，q坐标系的d轴上，一起以同步速旋转。

在这里假设电机的绕组是对称并且正弦分布的，同时忽略电机互感中的漏感及铁心损耗。电机两套定子绕组的坐标变换矩阵分别如下:

将静止的A，B，C绕组变换到同步速ω旋转的d，q坐标系的变换矩阵:

将静止的U，V，W绕组变换到同步速ω旋转的d，q坐标系变换矩阵:

根据上述坐标变换矩阵，将电机的定、转子矩阵变换到同步速旋转坐标系的d，q轴上。那么经过变换后，电机的磁链方程、电压方程、转矩方程分别如下所示。

磁链方程:

电压方程:

任意速旋转坐标系Ω下的双三相感应电动机电压模型如下:

转矩方程:

只有旋转电势和相应电流的乘积等于与电磁转矩对应的电磁功率，因此经坐标变换推导后，双三相感应电动机的电磁转矩方程:

从式(1)～式(3)可以看到，这种将双三相电机绕组分解到旋转的d，q坐标系上的方法，使得双三相感应电动机电压和磁链方程中的各个量成为与电机转子位置无关的常数。同时，电机电磁转矩成为了与正交坐标系下解耦的定子、转子绕组电流相关的变量，从而实现了双三相电机的解耦，同时大大简化了电机模型，为实现双三相感应电动机的矢量控制打下了良好基础。

2 双三相感应电动机磁链观测模型

根据上节介绍的双三相感应电动机在d，q坐标系下的数学模型，同时考虑到转子采用鼠笼转子的形式，那么udr=uqr=0;同时，以转子磁场矢量的方向作为 d轴，就可以得到:Ψdr=Ψr，Ψqr=0，由此电机转子磁链方程和电压方程:

将式(6)带入式(4)可以得到双三相感应电动机的转子磁链:

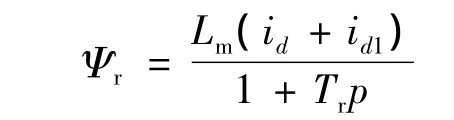
式中:Tr为转子电气时间常数，其定义:

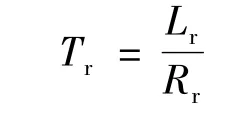
同时本文定义励磁电流:

由式(7)与式(5)经整理后可以得到:

因此双三相感应电动机的转差ωf可以表示:

则转子磁链的相位:

3 双三相感应电动机矢量控制系统仿真

根据上面介绍的双三相感应电动机模型及转子磁链观测的基本方法，针对一台3.6 kW的双三相感应电动机，如表1所示，设计了按转子磁场定向的矢量控制调速系统，控制系统框图如图2所示，其中磁链按照磁链的标么值给定。当电机运行在高速区时，可以通过减小磁链给定值的方法达到弱磁调速的目的;转矩给定值指电机负载转矩。

表1 双三相感应电动机参数

图2 双三相感应电动机调速系统

控制系统采用转速、电流双闭环控制技术，该控制系统的原理如下:首先，电机的给定转速与实际转速反馈值经过转速控制器的PI调节得到转矩给定值，并输入到转矩计算器模块得到q轴电流给定值;磁链给定值经过d轴电流计算模块得到的结果分别输入d轴电流控制器和d轴电流控制器1。d轴电流计算模块与转矩计算器模块均是按照本文介绍的双三相感应电动机在旋转dq轴模型下的数学模型确立的。磁链观测器模块则是根据电机转子磁链观测模型，计算得到了相应时刻转子磁链的空间位置。以上所得的各个电流给定值经过电流控制器模块计算可以得到各自的电压给定值，经过Park变换和Clarke变换(3/2变换)得到了在静止坐标系下电机各相的供电电压。在本文的仿真过程中，电机机械转速给定值为60 rad/s，仿真时间为1.2 s。首先，电机空载起动，在0.4 s时刻负载转矩达到60 N·m;在电机起动后0.8 s时刻电机的负载转矩下降到30 N·m。

在图2的控制方式下，双三相感应电动机的转速、转矩随时间变化的曲线如图3和图4所示;转子磁链标么值随时间变化轨迹及转子磁链圆轨迹分别如图5和图6所示。

图3 起动和负载突变时的转速变化

图4 起动和负载突变时的转矩变化

图5 转子磁链标么值－时间变化曲线

图6 转子磁链圆轨迹

通过以上仿真结果可以看到，电机空载起动，其转速响应在这个过程中超调很小，如图3所示，经过约90 ms的时间，电机转速响应到达了转速给定值60 rad/s;在电机起动0.4 s后，电机负载转矩突增，转矩响应经调整能够迅速达到负载转矩60 N·m;0.8 s时电机的负载转矩下降到30 N·m，转矩响应也能够快速跟踪负载转矩的变化达到新的稳定值。同时，在以上负载转矩切换的过程中，电机的转速响应能够一直稳定在60 rad/s的给定值。图3的转速波形及图4的转矩曲线表明，电机的转速脉动和转矩脉动都比较小，整个调速系统具有较好的动态和静态性能。

4 结 语

根据双三相感应电动机在静止坐标系下的数学模型，通过恰当的坐标变换，将双三相感应电动机的两套定子绕组和转子绕组变换到以同步速旋转的坐标系上;然后以电机转子磁场矢量的方向作为d轴，能够使原静止坐标系下耦合的双三相感应电动机的数学模型在该旋转坐标系上达到解耦的目的;根据上述电机模型，设计了双三相感应电动机矢量控制系统，其仿真结果表明，该调速系统具有良好的动态和稳态性能，适用于对双三相感应电动机的控制。

［1］LEVI E.Multiphase electric machines for variable speed applications［J］.IEEE Transactions on Industrial Electronics，2008，55(5):1893－1909.

［2］PARSA L.On advantages of multi－ Phase machines［J］.Industrial Electronics Society，2005，13(2):1574 －1579.

［3］刘东，黄进，杨家强.多相感应电机转子磁场定向矢量控制策略［J］.浙江大学学报(工学版)，2012，46(8):1498 －1505.

［4］许实章.交流电机的绕组理论［M］.北京:机械工业出版社，1985.

［5］ALFREDO R M，THOMAS A L.Dual stator winding induction machine drive［J］.IEEE Transactions on Industrial Applications，2000，36(5):1369 －1379.

［6］NELSON R H，KRAUSE P C.Induction machine analysis for arbitrary displacement between multiple winding sets［J］.IEEE Transactions on Power Apparatus and Systems，1974，93(3):841 －848.

［7］BOJOI R，TENCONI A，PROFUMO F.Complete analysis and comparative study of digital modulation techniques for dual three－ phase AC motor drives［J］.Power Electronics Specialists Conference，2002，2:851 －857.

［8］GIERSE G，SCHUERMANN W.Microprocessor control for two magnetically coupled three － phase PWM inverters［J］.IEEE Transactions on Power Electronics，1986(3):141 －147.

［9］HADIOUCHE D，BAGHLI L.Space － vector PWM techniques for dual three － phase AC machine:analysis，performance evaluation，and DSP implementation［J］.IEEE Transactions on Power Electronics，2006，42(4):1112 －1122.

［10］ZAIMEDDINE R，UNDELAND T.Direct torque control scheme for Dual Three Phase induction motor［C］//Power Electronics Conference(IPEC)，Sapporo，2010，21 －24:3007 －3014.

［11］LI Shan，XIAO Huihui.Research of SVPWM control technique of double three － phase induction motor［C］//Electrical Machines and System 2005(ICEMS 2005)，2005:109 －114.

［12］BOJOI R，LAZZARI M.Digital field oriented control for dual three phase induction motor drives［J］.IEEE Transactions on Industrial Electronics，2003，39(3):752－760.