(2+1)维破裂孤子方程组的精确解

王振立，刘希强

(2+1)维破裂孤子方程组的精确解

王振立，*刘希强

(聊城大学数学科学学院，山东，聊城 252059)

利用推广的()展开法，并借助于计算机代数系统maple，获得了（2+l）维破裂孤子方程组新的显式解，包括单循环孤立子解、三角周期解、有理函数解等。

(2+1)维破裂孤子方程组；()展开法；显式解；齐次平衡

寻找非线性偏微分方程的精确解在孤立子理论中一直占有重要地位。非线性偏微分方程描述了众多领域的复杂现象，如物理学，生物，化学，工程等。到目前为止已发展了许多不同的求解方法，如Painlevé截尾展开法[1]，双曲函数法[2-4]，Jacobi椭圆函数展开法[5]，Jacobi椭圆函数方法一般化的F-展开法[6]，反散射法[7]，齐次平衡法[8]等。利用这些方法得到许多丰富的精确解，包括孤立波解，周期波解等。

文献[9]中提出了一种新的构造精确行波解()的展开方法。该法的主要思想是：非线性演化方程的行波解可以表示为()的多项式，多项式的次数可由齐次平衡原则确定；多项式的系数可通过解一个非线性代数方程组求得；非线性代数方程组是应用()展开法过程中产生的。该方法具有直接、简洁与基本的优点，已有效地求解了许多非线性演化方程。本文应用()展开法获得了(2+1)维破裂孤子方程组含任意参数的更多的显式行波解。

1 (w/g)展开法

考虑如下偏微分方程

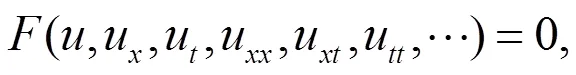
(ii)假设（1.2）有下述形式的解：

(1.3)

关于()的项共有+1项。这里的()满足以下方程

即

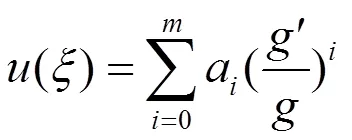
且满足

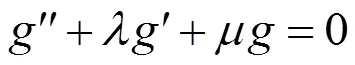
这是我们熟悉的tanh函数展开法[11-12]。

且满足

且满足

2 （2+1）维破裂孤子方程组的行波解

考虑以下方程组

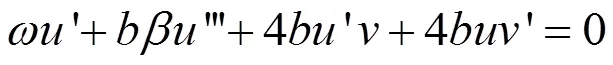
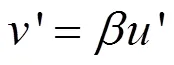
将(2.4)积分一次得

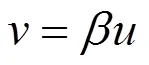
代入(2.3)式积分并置积分常数为零，得

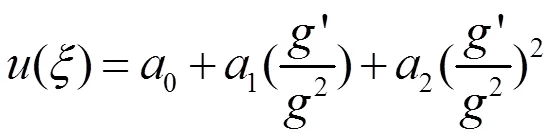
解以上代数方程组得：

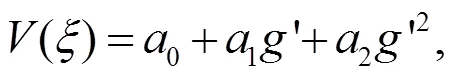
解以上代数方程组得：

注：(1)本文得到方程组显式解比文献[13]中的该类型的解丰富。

(2)本文得到的解均经过maple数学软件检验。

3 结论

()展开法的提出为非线性发展方程(组)的求解又提供了一种强有力的办法。本文将简洁的()展开方法应用于(2+1)维破裂孤子方程组的显式行波解，其中包括孤立波解、三角函数解以及有理函数解。由于参数的任意性, ()展开法可以获得(2+1)维破裂孤子方程组更多的精确解。这些精确解对解释复杂的物理现象有重要的作用。()展开法具有直接、简捷而基本的优点，该方法具有一定的普遍性，可以用来求解其它的非线性发展方程(组)。

[1] Weiss J,Tabor M, Carnevale G . The Painlevé property for partial differential equations[J]. Journal of Mathematical Physics, 1983, 24(3): 522-526．

[2] Parkes E J, Duffy B R. An automated tanh-function method for finding solitary wave solutions to non-linear evolution equations[J]. Computer Physics Communications, 1996, 98(3): 288-300.

[3] Abdusalam Η A. On an improved complex tanh-function method[J]. International Journal of Nonlinear Sciences and Numerical Simulation, 2005, 6(2): 99-106.

[4] Fan E. An algebraic method for finding a series of exact solutions to integrable and nonintegrable nonlinear evolution equations[J]. Journal of Physics A: Mathematical and General, 2003, 36(25): 7009-7016.

[5] Liu S, Fu Z, Liu S, et al. Jacobi elliptic function expansion method and periodic wave solutions of nonlinear wave equations[J]. Physics Letters A, 2001, 289(1): 69-74.

[6] Zhou Y, Wang M, Wang Y. Periodic wave solutions to a coupled KdV equations with variable coefficients[J]. Physics Letters A, 2003, 308(1): 31-36.

[7] Ablowitz M J, Segur H. Solitons and the inverse scattering transform[M]. Philadelphia: Siam, 1981.

[8] Fan E, Zhang H. A note on the homogeneous balance method[J]. Physics Letters A, 1998, 246(5): 403-406.

[9] Li W A, Chen H, Zhang G C. The (ω/g)-expansion method and its application to Vakhnenko equation[J]. Chinese Physics B, 2009, 18(2): 400-404.

[10] Wang M L, Li X, Zhang J.The(′/) -expansion method and travelling wave solutions of nonlinear evolution equations in mathematical physics[J].Physics Letters A,2008, 372(4):417-423.

[11] Fan E. Extended tanh-function method and its applications to nonlinear equations[J]. Physics Letters A, 2000, 277(4):212-218.

[12] Wazwaz A. Exact solutions for the ZK-MEW equation by using the tanh and sine–cosine methods[J]. International Journal of Computer Mathematics, 2005, 82(6): 699-708.

[13] Cao R. Exact Solutions for (2+1) Dimensional Breaking Soliton Equation[J]. University mathematics, 2012, 28(2):34-36.

Explicit Solutions of (2+1)-dimensional Breaking Solition Equations

Wangzhen-li，*LiuXi-qiang

（College of Mathematical Sciences，Liaocheng University, Liaocheng, Shandong 252059,China）

Applying the generalized () -expansion method and with the help of computer algebraic system maple, the explicit travelling solutions of the (2+1)-dimensional breaking solition equations were obtained, which included soliton solution, the trigonometric functions and the rational functions.

(2+1)-dimensional breaking solition equations; the ()-expansion method; explicit solutions; homogeneous balance principle

O175.2

A

10.3969/j.issn.1674-8085.2014.04.005

2014-03-28；

2014-05-15

国家自然科学基金和中国工程物理研究院联合基金项目(11076015)

王振立(1981- )，男，山东枣庄人，硕士生，主要从事非线性偏微分方程解的研究(E-mail: wzl2319668@163.com);

*刘希强(1957- )，男，山东菏泽人，教授，博士，主要从事非线性偏微分方程系统研究(E-mail:liuxiq@sina.com).