基于对数谱射频指纹识别的RFID系统信息监控方法

袁红林，包志华，严燕

(1. 南通大学 电子信息学院，江苏 南通 226019；2. 南通大学 计算机科学与技术学院，江苏 南通 226019)

1 引言

2002年，李衍达院士提出了应从信息的控制观点认识自动化学科的本质及其应用范围，指出网络化、集成化与智能化对自动化学科提出了巨大的挑战，也提供了重大机遇[1]。随着各种技术与应用的飞速发展，文献[1]的观点在很多方面得到了验证，典型实例包括网络的服务质量控制与用户身份认证等。其中，网络的用户身份认证一般基于密码机制与认证协议实现信息的控制。开始通信时，网络通信方通过挑战—应答的认证协议确认对方是否为合法用户，如是，则允许其加入网络并进行后续的信息交互；否则，拒绝其加入。然而，网络用户认证的这种信息控制方法具有以下缺点：1）认证协议本身容易存在中间人攻击等缺陷，从而使非法用户能参与信息交互而不被发现；2）任何获取了认证协议使用密钥的非法用户都有以合法用户身份进入网络而不被发现的可能性；3）仅在通信方入网时进行身份认证，非法用户一旦入网后将不会被发现。因此，传统的基于密码机制与认证协议的信息控制方法存在天然的不足。

作为一种简单的点对点网络，射频识别（RFID,radio frequency identification）系统对信息的控制也存在以上不足。RFID源于第二次世界大战中的敌我电台识别，是一种通过电磁场/波实现无接触信息传递的技术。RFID系统一般由读写器、标签与后台管理系统构成[2]。RFID系统中读写器与标签通过空气媒介进行通信，因此可能面临克隆、篡改、窃听、假冒与重传等攻击。未配备电池的无源RFID标签，通过电磁感应获得电源，可认为是一种辐射源，已广泛应用于身份证、护照及供应链系统等。无源RFID标签的资源极其有限，因此其对信息的控制难度更高。尽管一大批轻量级与超轻量级的密码与安全协议陆续被提出，仍不能改变基于密码与认证协议的信息控制方法的天然不足。

本文提出了无源 RFID标签的对数谱射频指纹变换方法以及基于此的无源 RFID系统的信息监测与控制方法。提出的方法把无源RFID标签作为一种辐射源，采用辐射源识别的方法识别或确认标签身份真伪，并结合RFID系统的应用层协议，实现标签与读写器之间信息流的监控。提出的方法不仅能增强开始通信时标签身份认证的安全性，而且在通信过程中也能对标签假冒事件给出警报，因此，无源RFID系统的信息监控强度与广度得到增强与拓展。

2 方法框架

基于辐射源识别的无源RFID系统信息监控方法的框架如图1所示。

如图1所示，提出方法框架包括无源RFID标签、读写器与射频指纹（RFF,RF fingerpint)[3]识别系统等，其中RFF识别系统由RFF变换、特征提取、识别或确认等构成。RFF变换部分采集无源RFID标签的辐射射频信号，把采集信号变换为体现标签硬件特征的RFF；特征提取部分对RFF进行特征提取；识别或确认部分根据特征对标签身份进行N:1的识别或1:1的确认，得到标签身份真伪结果；RFF、特征与标签身份真伪结果送到读写器的应用层协议与非法标签警报部分；读写器应用层协议融合标签身份真伪结果、RFF或特征实现与标签之间信息流的控制。

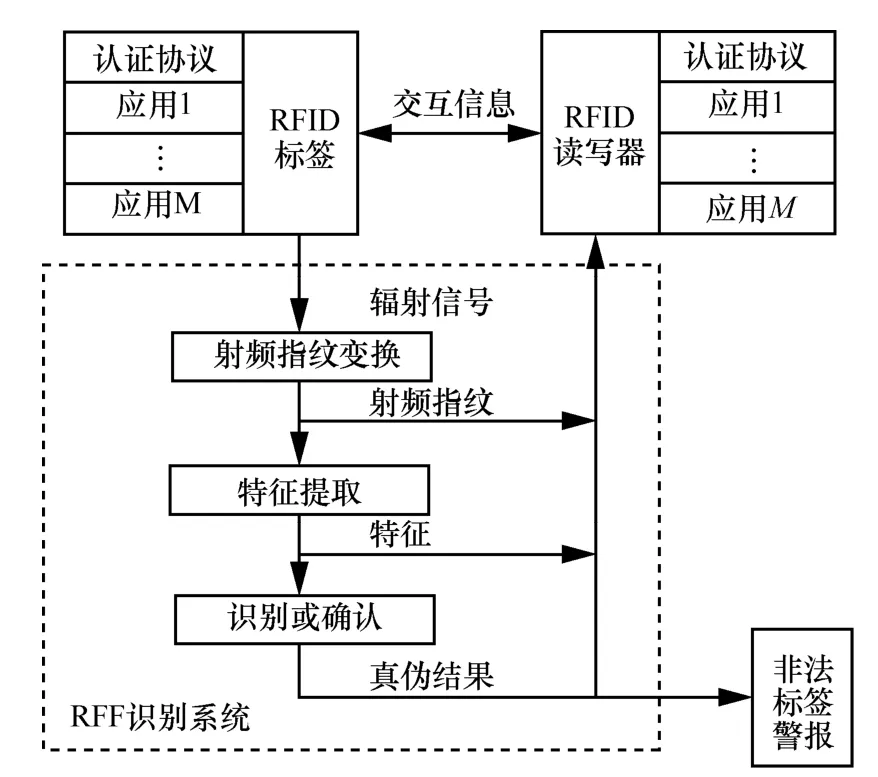
图1 提出方法的框架

3 无源RFID系统

无源RFID系统的标签一般没有供电电源。工作时，读写器发送电磁场，标签通过电磁谐振获得电源；读写器与标签之间通过负载调制进行双向信息传递。标签的附加负载电阻以一定的时钟频率接通和断开，从而在读写器发送频率两侧形成2条副载波谱线，标签基带数据传输通过对副载波进行振幅键控、频移键控或相移键控调制来完成。ISO 14443A是无源RFID系统的主要标准之一，其频谱示意如图2所示。

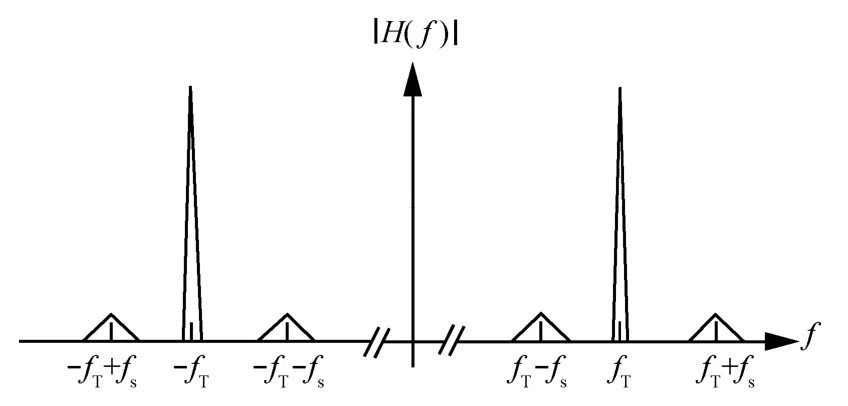
图2 ISO 14443A系统的频谱

图2中， fT=13. 56 MHz为读写器载波频率，fs=847. 5kHz为副载波频率，实际信息包含在2个副载波上、下边带中。ISO 14443A系统的一个实际射频信号及其延迟解调结果如图3所示。

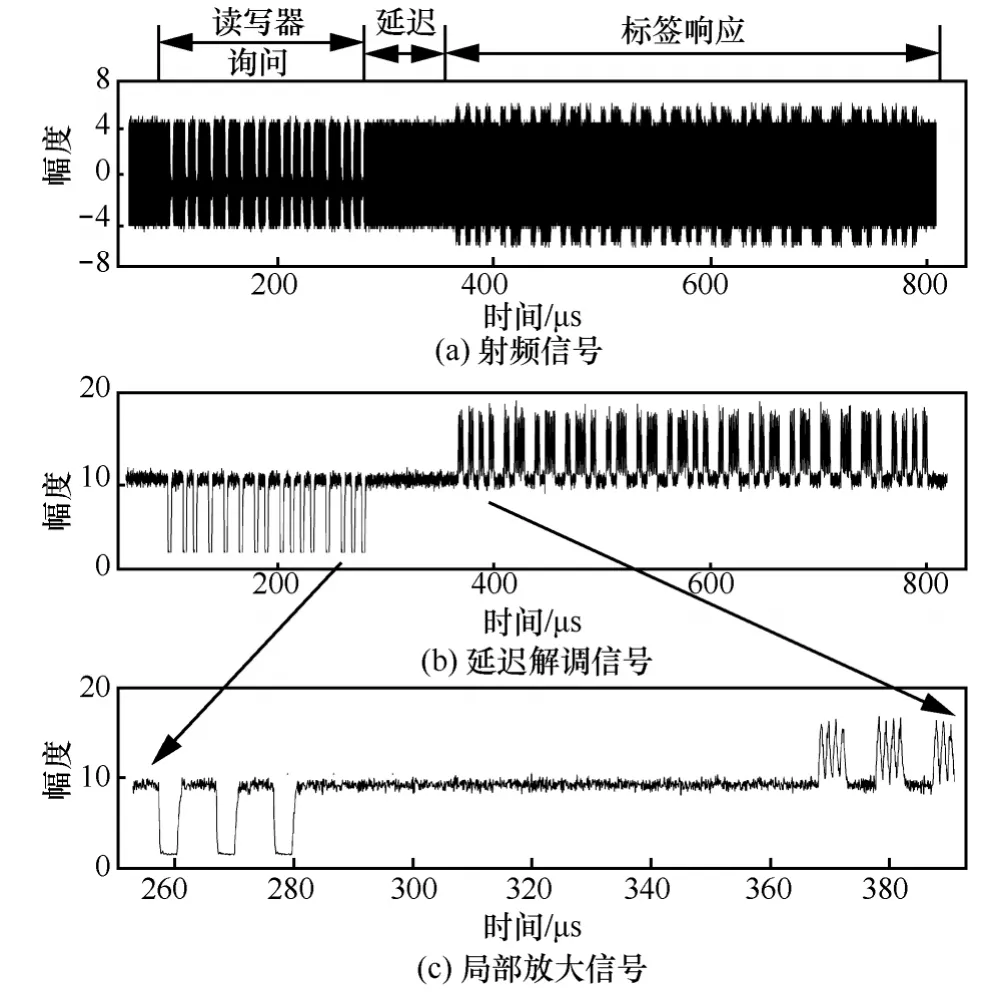
图3 一个ISO 14443A射频信号及其延迟解调实例

根据ISO 14443A标签信号的产生原理与频谱可知，其副载波的下边带或上边带信号可行为级描述为

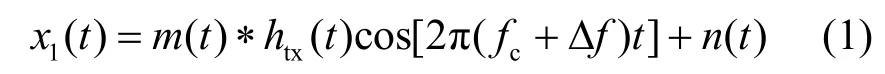
其中，m(t)为RFID标签发送的基带数字信号；htx(t)为标签发送电路的等效冲击响应； fc为标准规定的下边带或上边带频率；Δf为RFID系统实际谐振频率与fc之间的频率差；n(t)为加性高斯白噪声；*表示卷积运算。由图3及以上分析可知，ISO 14443A标签可视为一种辐射源，其辐射信号不仅携带着数字信息，而且携带着自身硬件信息[4]，因此，可变换其辐射信号为体现标签硬件特性的RFF，进而根据RFF实现标签身份的识别或确认。

4 对数谱射频指纹

辐射源RFF也叫辐射源指纹、信号指纹与设备指纹[5～7]，具体的辐射源 RFF包括雷达指纹[8,9]、电台指纹[10,11]、无线网卡指纹[12]与 RFID 标签指纹[3]等。文献[13]首次对基于RFF的RFID标签与无线网卡等无线设备的识别进行了综述；文献[3]基于动态小波指纹与有监督模式分类技术对 RFID标签进行识别，在一定的条件下获得了 99%以上的正确识别率；文献[14]把无源RFID标签不同谐振频点的最小功率响应作为一种RFF，获得了优秀的识别性能。

有关RFF的研究表明，不同RFF体现待识别辐射源的不同硬件信息，使用多种RFF进行融合识别或确认，能够提高辐射源的识别或确认性能[4]。

本部分把无源RFID标签的辐射信号变换为标签的对数谱参量，作为一种新的RFF，称为对数谱RFF，用于 RFID标签的识别，给出了变换方法与相应的数值仿真。

4.1 变换方法

无源RFID标签的对数谱RFF的变换结构如图4所示。

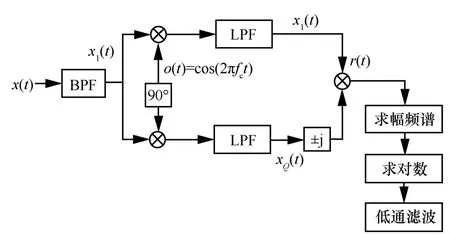
图4 无源RFID标签的对数谱RFF变换结构

图4中，x(t)为近耦合状态下采集的RFID标签的电磁辐射信号；x1(t)为经过带通滤波器 BPF后的副载波下边带或上边带信号；x1(t)经数字载波o(t)正交下变频并低通滤波(LPF)后构成复信号

式(2)中复信号r(t)的傅立叶变换表示为

其中，M(f)与Htx(f)分别为m(t)与htx(t)的傅立叶变换，N1(f)为噪声傅立叶变换项。对于一个确定的RFID读写器，式(1)中RFID标签的等效冲击响应htx(t)与频偏Δf由待识别标签的电路结构与其构件参数的实际值确定；由于构件容差等因素的存在，即使结构与构件标称值相同的同一型号不同标签的htx(t)与Δf也各不相同。因此，htx(t)与Δf为体现标签硬件性质的参量。

式(3)可表示为

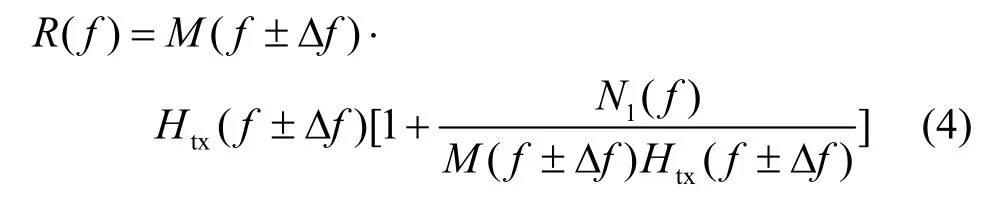
对式(4)进行求模与对数运算，结果为

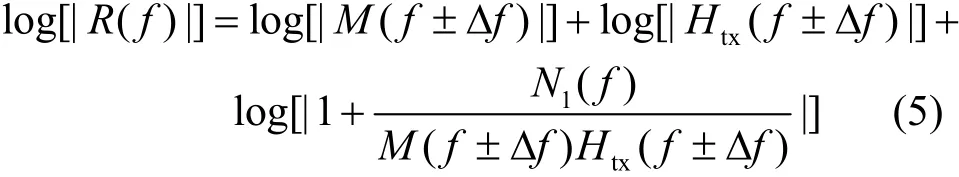
由式(1)可知，标签发送基带数字信号可等效表示为

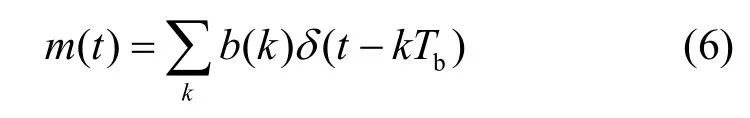
由上文可知，式(7)由RFID标签等效冲击响应htx(t)与频偏 Δf唯一确定。因此，L PF{log[|R(f)|]}可作为一种 RFF用于标签硬件的识别，LPF{log[|R(f)|]}即无源RFID标签的对数谱RFF。

无源RFID标签的对数谱RFF变换步骤总结如下。

步骤1 相对位置固定状态下，采集无源RFID系统的电磁感应射频信号。

步骤2 对射频信号进行带通滤波，截取下边带或上边带副载波信号。

步骤3 对副载波边带信号进行基于标准规定频率的正交下变频，并构成复信号。

步骤4 求复信号的幅度谱、对数，并进行低通滤波。

结果即无源RFID标签的对数谱RFF。由建模分析可知，对数谱RFF与基带数字信息无关，主要由RFID标签的硬件物理性质决定，对信号起始点检测精度不敏感，因而具有稳健性与时间平移不变性。

4.2 数值仿真

对无源RFID标签的对数谱RFF变换方法进行数值仿真。在Matlab环境下，根据式(1)产生x1(t)信号，基于图4所示的变换原理，按照对数谱RFF变换方法对x1(t)进行处理。其中发送基带数字信号m(t)的比特率为847.5 bit/s，标签发送电路的等效冲击响应htx(t)为21阶，滚降因子为0.5的滤波器，fT-fs为ISO 14443A标准规定的下边带中心频率12.7125 MHz，Δf为84.75 kHz，信噪比为0 dB，系统采样频率为127.125 Msample/s。一次仿真的部分结果如图5所示。

按照图5仿真条件进行50次蒙特卡罗仿真，每次仿真进行了如下操作：1)随机生成发送基带数字信号m(t)；2)在m(t)头部增加均匀分布的随机延迟，模拟采集的标签辐射信号起始时刻检测误差；3)加入不同的高斯噪声。仿真结果如图6所示。

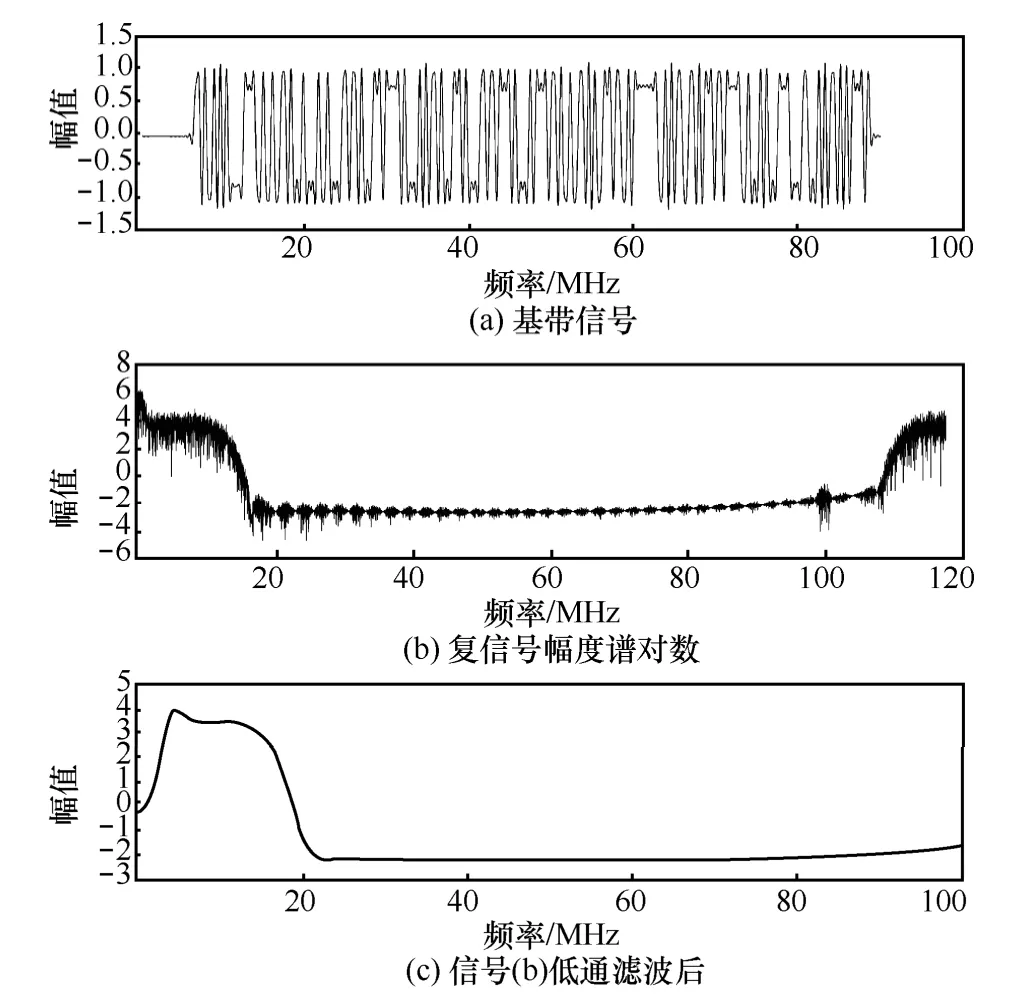
图5 一次对数谱RFF仿真

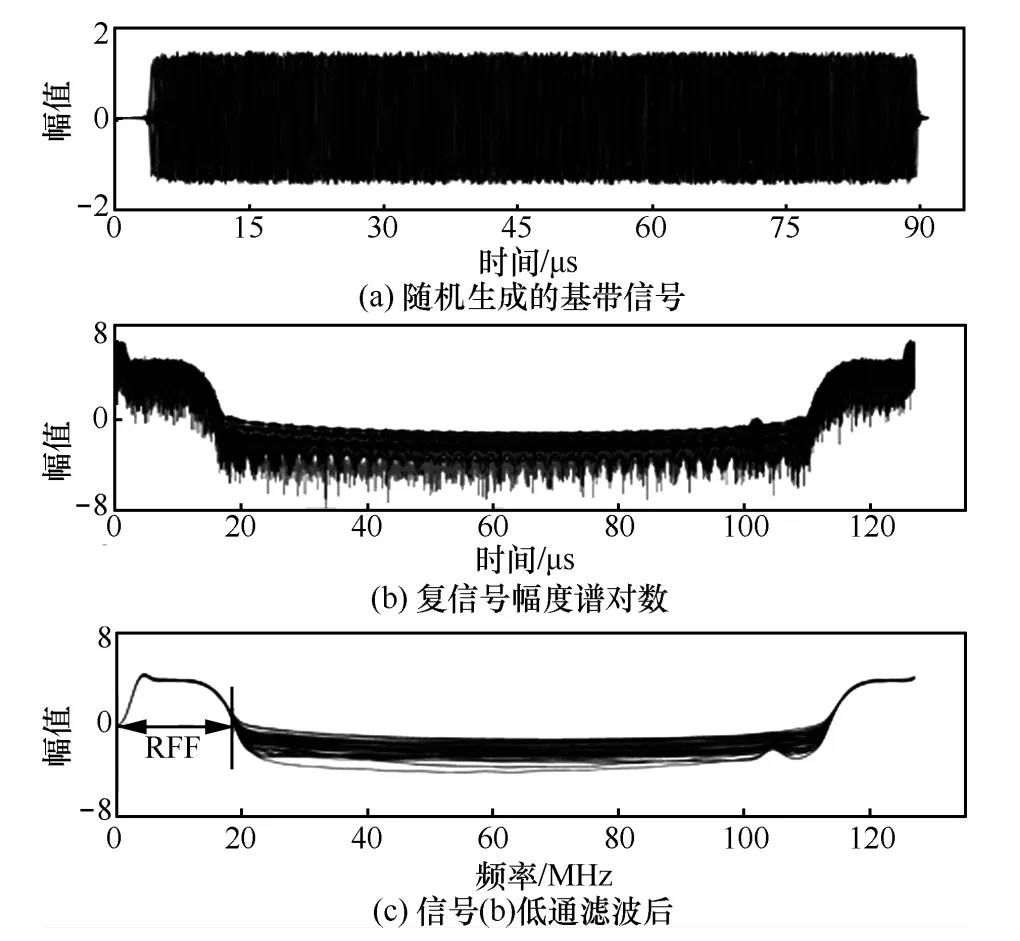
图6 对数谱RFF的蒙特卡罗仿真

图6中各子图对应图5中各子图。由图5(c)可知，复信号幅度谱的对数低通滤波后信号的能量主要集中在正幅值部分，并且其稳定性高；因此，截取其正幅值部分作为对数谱RFF。由图6可知，在信噪比较低（0 dB）的情况下，对数谱RFF仍具有消除基带数字信号影响，对信号起始点检测精度不敏感等优点，因此具备时间平移不变性与稳健性。

本部分对提出的无源RFID标签的对数谱RFF变换方法进行了建模分析与数值仿真，验证了其正确性与优点。

5 实验

本部分采用实验的方法对对数谱 RFF变换方法及后续的特征提取与分类进行研究，其中的特征提取与分类采用成熟的方法进行。

5.1 实验系统

ISO 14443A RFID系统的信号采集与标签的对数谱RFF实验系统如图7所示，包括RFID读写器、标签、示波器、计算机与天线等。

图7 RFID标签的对数谱RFF实验系统

图7中，计算机对ISO 14443A RFID读写器进行控制；射频示波器为带宽2 GHz的力科432，采样率为250 Msample/s，外接13.56 M天线线圈，射频示波器采集的信号通过有线网络送至计算机进行处理。实验时，读写器与标签的相对位置保持不变，并且对实验环境进行了电磁屏蔽与温度控制。

5.2 对数谱射频指纹变换

按照对数谱 RFF变换方法对采集的标签辐射信号进行实验。其中下边带带宽取950 kHz，下变频载波频率为12.72 MHz。一次标签对数谱RFF变换实验中间结果的局部信号如图8所示。

由图8(d)可知，其包含丰富的快变分量；图8(e)为log[|R(f)|]的低通滤波后信号，截取其正幅值部分，即无源RFID标签对数谱RFF。

5.3 特征提取

选取同一厂家同一系列的5个ISO 14443A标签，记为class 1至class 5，进行标签的对数谱RFF变换与RFF的特征提取实验。

每个标签采集50个射频信号样本，采集时间跨度为3个月，并分别变换为对数谱RFF LPF{log [|R(f)|]}。对每个 LPF{log[|R(f)|]}进行基于相似因子的特征提取[16]，即把 LPF{log[|R(f)|]}对矩形基与三角形基的投影Cr1与Cr2（0≤Cr1≤1，0≤Cr2≤ 1）作为特征矢量[Cr1,Cr2]，Cr1与Cr2分别体现了LPF{log[|R(f)|]}形状与矩形及三角形形状的相似程度。5个标签的250个[Cr1,Cr2]分布如图9所示。

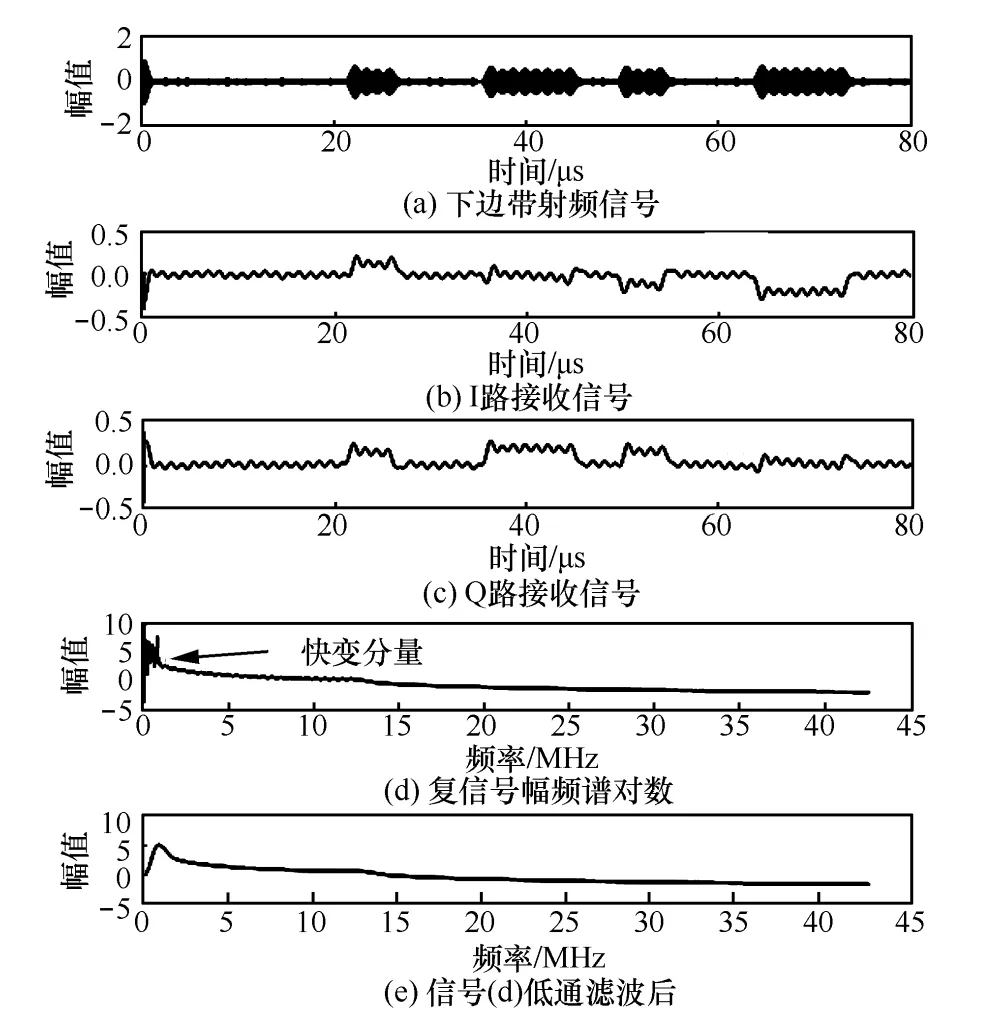
图8 一次标签对数谱RFF变换实验中间结果的局部信号

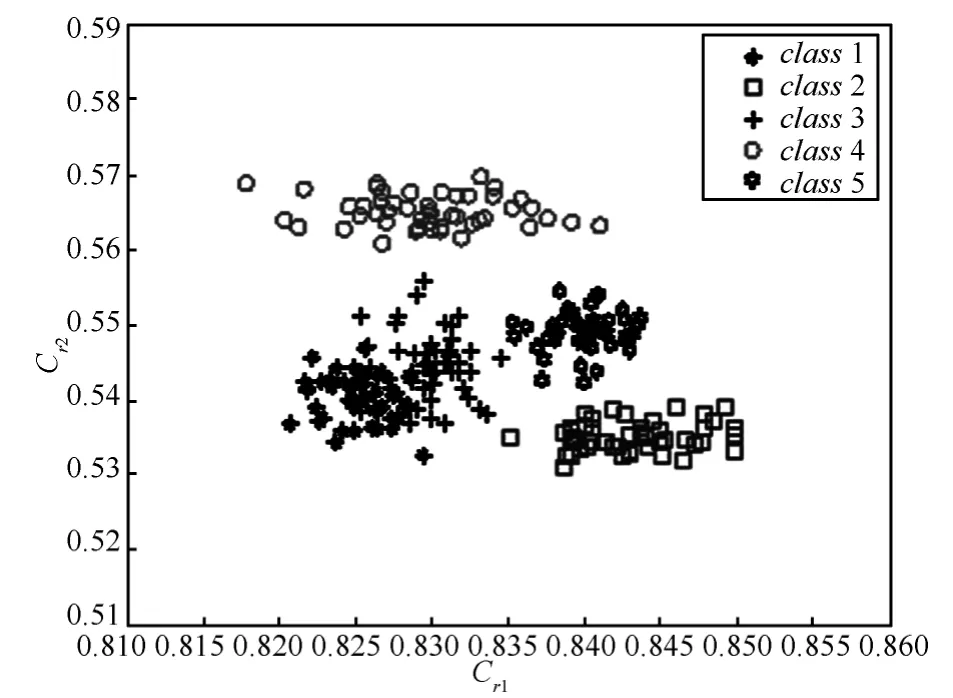
图9 5个标签的[Cr1,Cr2]分布

由图9可知，大部分标签的对数谱RFF的相似因子特征具有好的可分性。

5.4 分类

基于最小二乘支持向量机(SVM,support vector machines)对5个ISO 14443A标签的对数谱RFF的相似因子特征进行分类实验。最小二乘SVM(LS—SVM)把解二次规划问题转化为求解线性方程组问题，提高了求解问题的速度和收敛精度。

使用 LS-SVMlab工具箱[17]对 5个标签的相似因子特征进行分类，每个标签为一个类。实验中，从每个标签的相似因子特征中随机选取k=25,…,3 0个特征作为训练集，剩余50-k个特征作为测试集。利用网格搜索与交叉寻优对正则化参数γ和核参数σ2进行优化，并且使用最小分类输出方案对数据集进行编码，以达到多类分类目的，3次分类实验结果如表1所示。

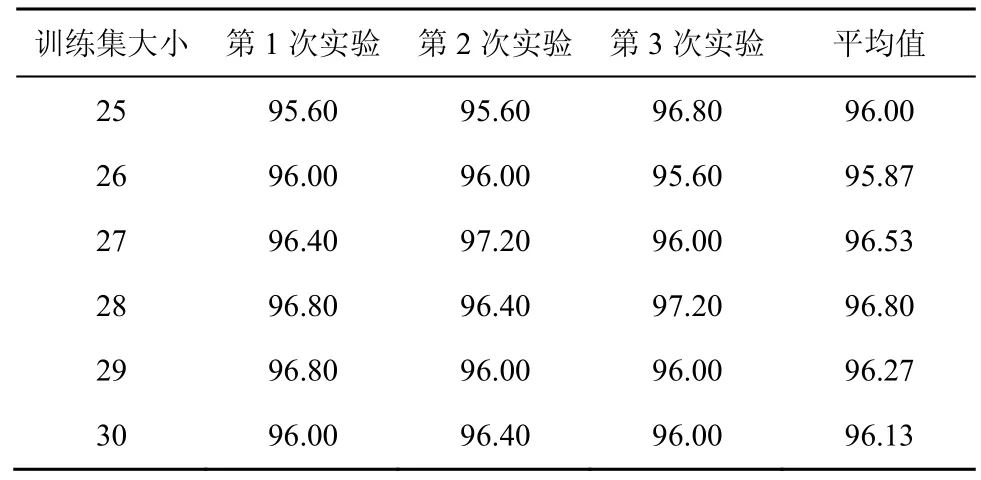
表1 5个标签的相似因子特征分类结果/%

表1中，由于不同分类实验中网格搜索与交叉择优得到的参数不同，因此分类结果具有随机性。由表1可知，采用提出RFF与其相似因子特征，当训练样本从25增加到30时，SVM分类器的结果没有大的改变，总体来看，该5个标签的正确识别率高。

尽管本文仅选用了5个ISO 14443A标签进行实验，然而，有关RFF唯一性的研究表明，RFF具有哲学意义上的唯一性。本文实验体现了提出方法的可行性。

6 融合射频指纹的RFID挑战—应答认证协议

RFID认证协议一般涉及读写器、标签与后台数据库三方，其中，读写器与后台数据库之间认为是安全信道。RFID认证协议的核心是通过挑战—应答机制实现读写器与标签之间的身份认证。本部分介绍经典的挑战—应答认证协议，给出融合提出RFF的RFID挑战—应答认证协议实例。

6.1 经典的挑战-应答认证协议

needham-schroeder公钥认证协议[18]是著名的挑战—应答认证协议，该协议在运行多年后被发现存在中间人攻击的缺陷，其改进版本克服了这种攻击，称为needham-schroeder-lowe协议，新协议仍由3条消息构成，如图10所示。

图10中，A与B为通信主体；在一次A与B的认证会话中，A与 B仅能申请到双方的公钥 Ka与Kb；Na与Nb分别为A与B产生的新鲜随机数；表示Na与A经Kb加密后消息；类似地，也是加密后消息；横线表示通信方之间的消息；竖线表示通信方进程。如图10所示，A产生Na，生成并发送至B发起认证；B用 Kb解密消息后，产生 Nb，生成并返回；A用Ka解密后，得到Na，从而确信对方就是B，因为只有B能解密消息获得Na，而 Na正是己方在上一条消息中发送出去的；A生成并发送，B收到消息后解密得到Nb，从而确信对方就是A，因为只有A能解密消息获得Nb，而Nb正是己方在上一条消息中发送出去的。这样，双方认证了对方身份，并且建立了双方共享的秘密Na与Nb，Na与Nb可用于后续通信中的消息认证。

图10 needham-schroeder-lowe认证协议

以上 needham-schroeder-lowe协议中，如果攻击者 P获得了通信一方的包括公钥在内的所有信息，则P可以假冒为该通信方通过另一方的认证，从而实现身份假冒攻击，这种由于密钥泄露导致的认证失败问题至今仍是一个难以解决的公开问题。

6.2 融合提出射频指纹的RFID needham-schroederlowe认证协议

融合提出RFF的RFID needham-schroeder-lowe认证协议如图11所示。

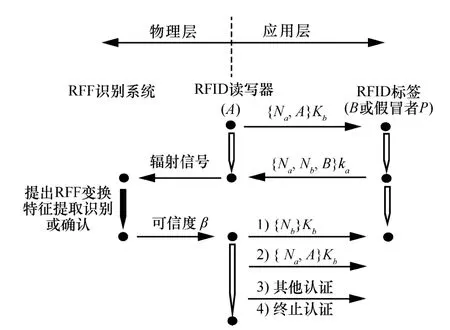
图11 融合提出RFF的RFID needham-schroeder-lowe认证协议

如图 11所示，新协议由应用层消息与物理层信号两部分构成；其中的RFID读写器即原协议的A通信方，RFID标签即原协议的 B通信方，RFF系统即图1提出方法框架中的RFF识别系统。新协议分为初始化与运行2个阶段。在协议初始化阶段，RFF系统获取目标RFID标签的多个辐射射频信号样本，变换为对数谱RFF，并进行对数谱RFF的特征提取，把得到的特征矢量集作为训练样本集存储在RFF系统中。

由第4部分的实验研究可知，基于ISO 14443A RFID标签的对数谱RFF、相似因子特征与SVM分类器，选取的5个标签的正确识别率达到95.60%～97.20%；当该 5个标签参与以上融合对数谱 RFF的RFID needham-schroeder-lowe认证协议时，一次认证中，合法标签能以高概率通过认证，而假冒标签能以高概率被检出并终止认证。

因此，融合了RFF的RFID needham-schroederlowe认证协议具有实现标签高强度认证的潜力，有助于抵抗有关标签假冒的绝大部分攻击，包括 克隆、重放、侦听、拒绝服务等，并且有助于进行密钥泄露检测，实现RFID系统信息流的控制。

尽管基于挑战—应答的其他RFID认证协议不一定与 needham-schroeder-lowe认证协议相同，但都可以采用以上方法融合标签的 RFF进行其身份的高强度认证。 另外，采用以上方法，图 1所示提出方法框架中RFID读写器的其他应用也可集成标签的RFF、特征或标签身份真伪结果，实现RFID系统通信过程中的标签身份认证与信息流控制。

7 结束语

本文提出了无源RFID标签的对数谱射频指纹变换方法，以及基于此的无源RFID系统的信息监控方法。提出的对数谱RFF主要由标签的硬件物理属性决定，与基带数字信号无关，具有对接收信号起始点检测精度不敏感，在低信噪比时仍具备稳健性的优点；提出的无源RFID系统的信息监控方法融合了通信应用层消息与物理层硬件信息，具有增强标签认证强度的特点，并且在通信过程中也能对标签身份真伪进行监控；给出了融合RFF的RFID挑战—应答认证协议实例。提出的标签 RFF以及RFID系统的信息监控方法可作为其他网络安全手段的一种有效补充，用于包含网络所有层的跨层整合与网络电子取证等；本文提出的融合RFF的通信方认证方法对于解决密钥泄漏检测公开问题也具有一定贡献。

与其他辐射源识别类似，RFID标签的正确识别或确认率不一定总能达到 100%。然而，可以使用多种RFF进行单个标签身份的融合识别或确认，这是进一步的研究工作。另外，本文仅采用了一种特征提取与分类方法，融合多种特征与多种分类方法具有提高识别率的潜力，这也是进一步的研究工作。现阶段的应用中，正如第6节介绍的融合RFF的挑战—应答认证协议实例所示，可通过发起多次认证提高可靠性，当然，新方法不可避免地增加了系统开销。

本文提出方法仅对 RFID标签 RFF进行了研究，也可获取RFID读写器的射频信号并进行类似的RFF变换、特征提取与分类等，从而实现对RFID读写器的高强度认证与信息流监控，提出方法及应用也可推广到其他的无线或有线通信系统中。

[1]李衍达. 从信息的控制观点看自动化的机遇与挑战[J]. 自动化学报,2002,28(s1):4-6.LI Y D. The opportunity and challenge for automation from the information control point of view[J]. Acta Automatica Sinica,2002,28(s1):4-6.

[2]王远哲,毛陆虹,刘辉等. 基于参考标签的射频识别定位算法研究与应用[J]. 通信学报,2010,31(2):86-92.WANG Y Z,MAO L H,LIU H,et al. Research and application of RFID location algorithm based on reference tags[J]. Journal of Communication,2010,31(2):86-92.

[3]BERTONCINI C,RUDD K,NOUSAIN B,et al. Wavelet fingerprinting of radio-frequency identification (RFID)tags[J]. IEEE Transactions on Industrial Electronics,2012,59(12):4843-4850.

[4]YUAN H L,BAO Z H,HU A Q. Power ramped-up preamble RF fingerprints of wireless transmitters[J]. Radio Engineering,2011,20(3):703-709.

[5]蔡忠伟,李建东. 基于双谱的通信辐射源个体识别[J]. 通信学报,2007,28(2):75-79.CAI Z W,LI JID. Study of transmitter individual identification based on bispectra[J]. Journal on Communications,2007,28(2):75-79.

[6]蒋鹏. 雷达信号细微特征分析与识别[D]. 哈尔滨: 哈尔滨工程大学,2012.JIANG P. Subtle Characteristic Analysis and Recognition of Radar Signals[D]. Harbin: Harbin Engineering University,2012.

[7]韩韬,周一宇. 雷达信号的扩散特征及其在特定辐射源识别中的应用[J]. 电子学报,2013,41(3):502-507.HAN T,ZHOU Y Y. Diffusion features in radar specific emitter identification[J]. Acta Electronica Sinica,2013,41(3):502-507.

[8]王磊,史亚,姬红兵. 基于多集典型相关分析的雷达辐射源指纹识别[J].西安电子科技大学学报,2013,40(2):164-171.WANG L,SHI Y,JI H B. Specific radar emitter identification using multiset canonical correlation analysis[J]. Journal of Xidian University,2013,40(2):164-171.

[9]刘海军,柳征,姜文利等. 基于联合参数建模的雷达辐射源识别方法[J]. 宇航学报,2011,32(1):142-149.LIU H J,LIU Z,JIANG W L,et al. A joint-parameter modeling based radar emitter identification method[J]. Journal of Astronautics,2011,32(1):142-149.

[10]唐智灵,杨小牛,李建东. 基于顺序统计的窄带通信辐射源指纹特征抽取方法[J]. 电子与信息学报,2011,33(5):1224-1228.TANG Z L,YANG X N,LI J D. A novel method based on order statistics for extracting fingerprint of narrow band emitter[J]. Journal of Electronics & Information Technology,2011,33(5):1224-1228.

[11]钱祖平,许渊,邵尉等. 基于高阶谱和时域分析的电台稳态特征提取算法[J].电子与信息学报,2013,35(7):1599-1605.QIAN Z P,XU Y,SHAO W,et al. Extraction algorithm of radio steady state characteristics based on high order spectrum and time-domain analysis[J]. Journal of Electronics & Information Technology,2013,35(7):1599-1605.

[12]黄光泉,王丰华,黄知涛. 一种基于分形维数的无线网卡信号指纹特征提取方法[J]. 电子对抗,2012,(5):25-27.HUANG G Q,WANG F H,HUANG Z T. A method of fingerprints extraction for WLAN cards based on fractal dimensions[J]. Electronicwarfare,2012,(5):25-27.

[13]DANEV B,ZANETTID,CAPKUN S. On physical-layer identification of wireless devices[J]. Acm Computing Surveys,2012,45(1): 1-31.

[14]PERIASWAMY S C G,THOMPSON D R,DI J. Fingerprinting RFID tags[J]. IEEE Transactions on Dependable and Secure Computing,2011,8(6):938-943.

[15]SCHAFER R W. Echo Removal By Discrete Generalized Linear Filtering[D]. Massachusefts Institute of Technology,1969.

[16]ZHANG G X,JIN W D,HU L Z. Resemblance coefficient based intrapulse feature extraction approach for radar emitter signals[J].Chinese Journal of Electronics,2005,14(2):337-340.

[17]SUYKENS J,MOOR B D,VANDEWALLE J. Least squares-support vector machines Matlab/C toolbox[EB/OL]. http://www.esat.kuleuven.be/sista/lssvmlab/,2013.

[18]张玉清,王磊,肖国镇等. Needham-Schroeder公钥协议的模型检测分析[J].软件学报,2000,11(10):1348-1352.ZHANG Y Q,WANG L,XIAO G Z,et al. Model checking analysis of needham-schroeder public-key protocol[J]. Journal of Software,2000,11(10):1348-1352.