推荐冲刷深度计算公式的应用浅析

高 波

（陕西水环境工程勘测设计研究院 陕西 西安 710018）

1 前言

河流是人类的重要自然资源，然自古实践证明，河流在自然状态下很难满足人类活动的需要。河道整治就是通过一定的措施，按照人类不同的需求，改变河流的某些自然状态，以期变水害为水利，从而实现为人类服务的目的。河道整治是治理河流的综合措施之一，按其目的可分为：①以防洪为目的的河道整治；②以改善航运条件为目的的河道整治；③以引水灌溉、工业及生活用水为目的的河道整治等。

堤防是沿河流、湖泊、海洋的岸边或蓄滞洪区、水库库区的周边修筑的挡水建筑物，它是人类自古以来广泛采用的一种重要的工程防洪措施，主要用于洪水整治。

综上所述，堤防工程应隶属于河道整治的范畴，是河道整治的一项工程措施。基于此，在《堤防工程设计规范》GB50286-2013（以下简称《堤防规范》）及《河道整治规范》GB50707-2011（以下简称《河道规范》）中均推荐了顺坝或平顺护岸的冲刷深度计算公式，笔者认为，两个规范中所推荐的公式尽管形式不同，但可通用。然而在具体的工程设计中，亦发现两个公式计算结果又有差别，以下是对两个规范所推荐公式的探讨和分析，希望能对工程设计提供一定参考。

2 公式探析

2.1 《河道整治规范》推荐公式

在《河道规范》附录B.2节推荐了冲刷深度计算公式，具体如下：

（1）B.2.1水流平行于防护工程产生的冲刷深度可按下式计算：

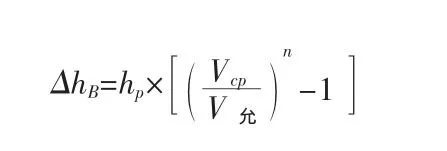
式中，ΔhB——局部冲刷深度（m）；

hP——冲刷处冲刷前的水深（m）；

Vcp——平均流速（m/s）；

V允——河床面上允许不冲流速（m/s）；

n——与防护岸坡在平面上的形状有关，可取n=1/4。

（2）B.2.2水流斜冲防护工程产生的冲刷深度可按下式计算：

式中，α——水流流向与岸坡交角（度）；

hp——从河底算起的局部冲深（m）；

m——防护建筑物迎水面边坡系数；

d——坡脚处土壤计算粒径（m）。对于非粘性土，取大于15%（按重量计）的筛孔直径，对于粘性土按照规范要求取当量粒径值；

Vj——水流的局部冲刷流速（m/s）。

（3）B 2.3水流的局部冲刷流速Vj的计算应符合下列要求：

若为滩地河床，Vj可按下式计算：

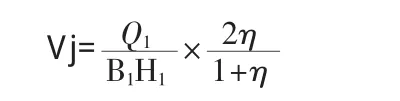
式中，B1——河滩宽度，从河槽边缘至坡脚距离（m）；

Q1——通过河滩部分的设计流量（m3/s）；

H1——河滩水深（m）；

η——水流流速分配不均匀系数，根据α角按表B.2.3采用。

若是无滩地河床，Vj可按下式计算：

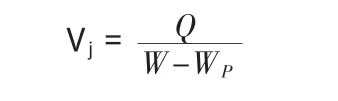
式中，Q——设计流量（m3/s）；

W——原河道过水断面面积（m2）；

WP——河道缩窄部分的断面面积（m2）。

在以上各式中：公式B.2.1来源于《水力计算手册》，其最初是用来计算建桥或渡槽后的桥（槽）墩冲刷深度的。n的取值则是参照《公路设计手册》——路基一书中有关桥墩平面形态与水流主流主向交角的关系，认为岸坡防护建筑物（顺坝或平顺护岸）在平面上的形状，近似为半流线形桥墩，故近似取n=1/4。公式在应用中存在的主要问题是：公式反映的指标较少，且指数“n”的取值和意义也还值得商榷。然而该公式在多年的实践中应用中，计算结果基本能够反映河道冲刷的实际情况，是目前实践应用最广泛的公式。

公式B.2.2最早的中文描述源于安德列耶夫、亚罗斯拉采夫合写的“桥渡建筑物所在河段的河床变形”一文中，从文中可推断公式B 2.2是从桥渡冲刷公式演化而来的。根据在我国实际运用的经验，上世纪60年代末就对亚罗斯拉夫采夫公式从理论上和实际运用上进行过评价：公式系根据没有泥沙进入冲刷坑的情况下导出的。在应用中存在着受水流流速及河床粒径d影响较大的弊端，具有一定的局限性。

2.2 《堤防设计规范》推荐公式

在《堤防规范》附录D.2节推荐了冲刷深度计算公式，具体如下：

D.2.2顺坝及平顺护岸冲刷深度计算可按下列公式计算：

表1 水流流速不均匀系数

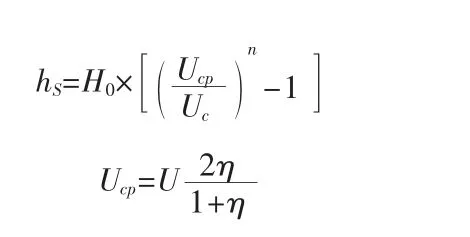
式中，hs——局部冲刷深度（m）；

H0——冲刷处的水深（m）；

Ucp——近岸垂线平均流速（m/s）；

Uc——床面上泥沙的起动流速（m/s），对于粘性与砂质河床可采用张瑞瑾公式计算；

n——与防护岸坡在平面上的形状有关，取1/4～1/6；

U——行近流速（m/s）；

η——同公式B.2.2中η意义。

对比《河道规范》公式B.2.1和公式《堤防规范》D.2.2，两个公式形式相同，各个计算参数的意义也相同，相应的两个公式出处亦相同。但公式D.2.2将水流平冲与斜冲计算合二为一，将斜冲与平冲用流速分配系数区别，在实践应用中更加直观，便于理解和操作。另该公式给出了UC的计算公式，相对于《河道规范》的不冲流速V允更具准确性。

3 公式计算结果对比分析

为了对比上述两规范所推荐公式对河道水流冲刷计算结果的差异，特选取两个典型工程，分别采用不同公式进行计算，分析其不同。

3.1 陕西省太白县石头河桃川镇杨下村段防洪工程

该工程位于太白县石头河桃川镇杨下村，设计为新修护岸工程，本文所选工程两个典型断面0+578和2+078分别位于工程区的水流平冲段和斜冲段，两处断面均为无滩单一断面，工程冲刷处河床质为漂（卵）石，其中河床质d50为4cm，d85为20cm。

3.2 陕西省绥德县义合河义合镇段防洪工程

该工程位于绥德县义合河义合镇，设计为新修堤防工程。本文所选工程两个典型断面0+720和0+250分别位于工程区的水流平冲段和斜冲段，两处断面均为无滩单一断面，工程处设计堤基为砂砾石，其中河床质d50为0.3cm，d85为15cm。

两处工程计算对比表具体见表2～4。

经过以上三表对比可见，在水流与堤岸夹角小于15°时，在《堤防规范》中水流分配不均匀系数η均取1，相当于《河道规范》中顺流冲刷计算公式，此时两个规范公式中其冲刷计算结果均取决于水流行近流速和河床质的不冲流速。故两个公式的计算结果基本相同。

当水流与堤岸夹角大于15°时，在《堤防规范》中采用η值来分配水流的斜冲流速，计算公式不变。而《河道规范》中采用B.2.2公式计算，在此公式中，河床对水流的抗冲能力概化为f(d)=30 d，导致该公式具有一定的局限性，当d较大或者较小时都可能出现异常的计算结果。正如前述实例计算所示，在石头河工程段取d=20cm时，计算结果出现了-0.9 m，相当于河道不会冲刷，而在绥德县义合河工程段取d=15cm时，计算结构出现了4.87 m的冲刷深，亦与工程区调查的多年平均冲刷深3.0 m有较大的出入。

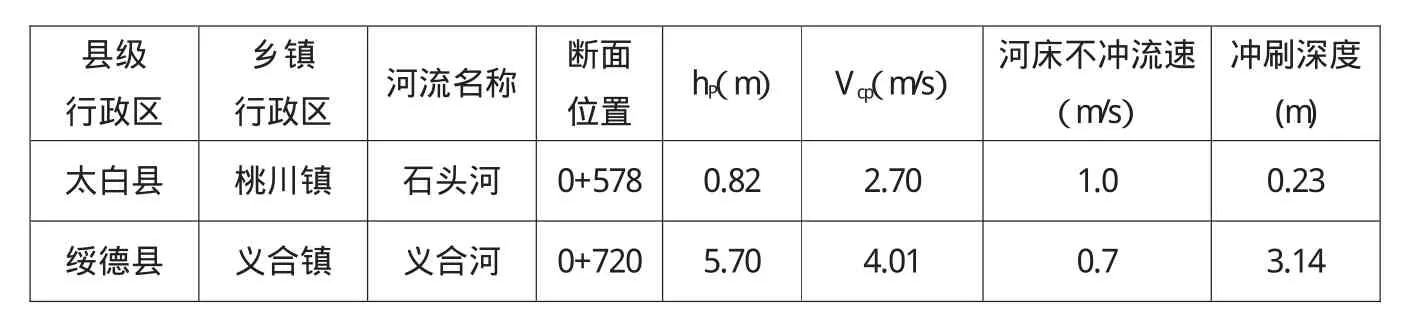
表2 《河道规范》顺流冲刷深度计算成果表

表3 《河道规范》斜流冲刷深度计算成果表

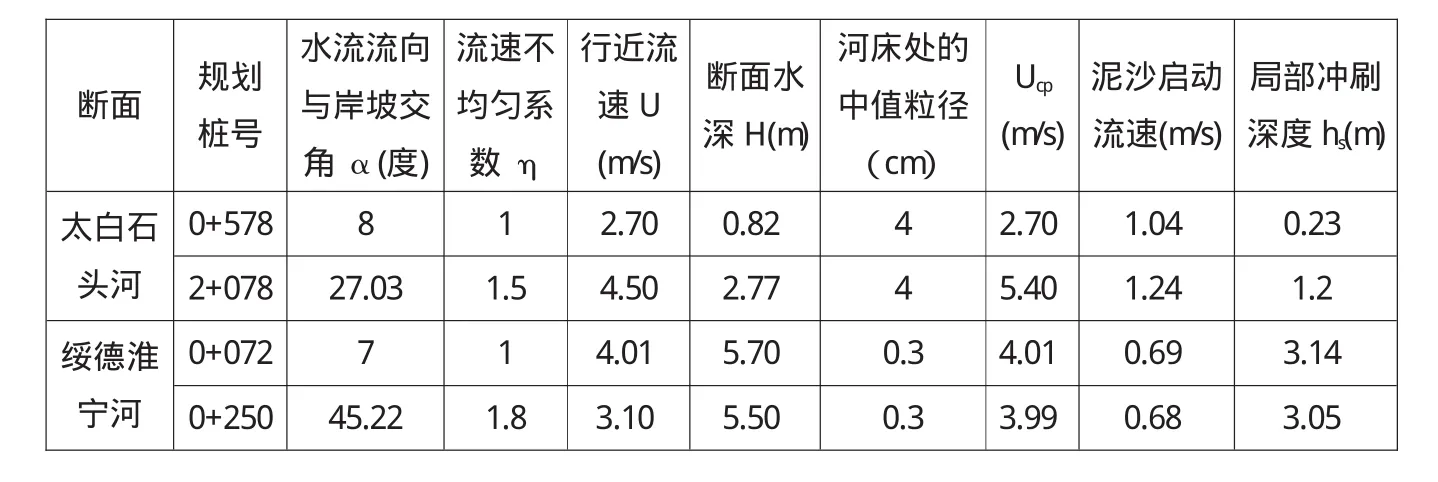
表4 《堤防规范》冲刷深度计算成果表

综上所述，两个规范公式在计算顺流冲刷时，公式反映的意义及考虑的参数基本相同，计算结果差别不大。而在河道斜冲河段，由于两个公式考虑的因素不同，计算结果往往不同。分析原因，主要是《河道规范》公式用30 d来反映河床的抗冲能力，具有一定的局限性。《堤防规范》计算公式主要受Ucp与Uc比值的影响，当河床质d50选定后，Ucp与Uc呈正比例变化，计算结果不会出现负值等不正常数据，根据作者以往的计算经验，认为《河道规范》公式应用于河床泥沙颗粒粒径在0.1 m～0.01 m范围内时，公式的稳定性较好。《堤防规范》公式则可应用于所有河段，具有更广阔的应用性。

4 公式应用的注意事项

目前，两个规范推荐公式都在水利部门应用普遍，如果在实践中运用其进行冲刷计算，需注意以下几点：

（1）无论应用《堤防规范》还是《河道规范》计算公式，在计算时均应注意对工程河段河势的分析，注意结合河道河势多年的变化趋势及工程修建后的河势预估，准确判断工程地处滩地段还是河槽段，滩地是假滩还是多年形成的稳定河滩等，从而准确应用公式及计算结果，确定建筑物基础的埋置深度，避免因河势判断不清而导致的基础埋置过浅或过深。

（2）注意对公式中各参数意义的理解，作者认为，在应用中存在的主要问题包括以下几个计算参数：①河床粒径d，《堤防规范》中d的取值为d50对应数值，而《河道规范》中d的概念为大于15%（按重量计）的筛孔直径，取值应为颗分曲线中d85对应数值。②《堤防规范》公式中在计算河床启动流速时，河道断面水深为计入行近流速的水深，在计算中很多人往往会忽视行近水头，而实际上，该水头对计算结果是有一定影响的。

（3）要注意对河道水流趋势的判断，一般当河道洪峰流量较大、水流流速大时，水流取直趋势较强；当洪水流量接近造床流量时，河床变形强烈，主流摆动较大，可能形成较大的迎冲角；另外，应注意分析建筑物对河道水流的影响作用，判断是否会形成折冲水流等。

[1]堤防工程设计规范GB50286-98[S].1998.

[2]堤防工程设计规范GB50286-2013[S].2013.

[3]河道整治规范GB50707-2011[S].2011.

[4]李晓庆，唐新军.对《堤防工程设计规范》推荐冲刷深度公式的探析[J].水资源与水工程学报，2006.04.

[5]武汉水利电力学院.水力计算手册[M].北京：中国水利水电出版社，1983.

[6]交通部第二公路勘察设计院.公路设计手册——路基（第二版）[M].北京：人民交通出版社，1996.

[7]武汉水利电力学院.河流泥沙动力学（下册）[M].北京：水利水电出版社，1982.

[8]水利电力部黄河水利委员会.河道整治[M].郑州：黄河水利出版社，1985.

[9]武汉大学.治河防洪工程[M].北京：中国水利水电出版社，2004.

[10]高波，刘彬侠等.陕西省太白县石头河重点段防洪工程初步设计[R].西安：陕西水环境工程勘测设计研究院，2011.06.

[11]高波，吕永乐等.陕西省绥德县义合河义合镇、满堂川乡集镇防洪工程初步设计[R].西安：陕西水环境工程勘测设计研究院，2012.06.