朗伯圆锥激光二维距离像仿真
宫彦军
(湖南科技学院 电子工程系,湖南 永州 425199)
引 言
目标一维距离成像最早是在雷达微波波段开展研究工作[1]。当雷达的距离分辨单元远小于目标尺寸时,目标会占据雷达的多个分辨单元,测量的雷达信号能反映目标在雷达径向上的投影,即距离剖面图(range profile),也称为一维距离像[1,2]。它能反映出目标沿雷达径向方向的精密几何结构分布。1989 Knight F.K 等人[3]通过一维距离分辨雷达数据重构二维图像。1999年Youmans D.G.等人[4]研究了利用二维距离像进行目标识别。国内关于激光雷达测距研究,中国科学院上海天文台首次建立了一套白天卫星激光测距系统[5]。2007年 Blanquer E.[6]通过二维距离像(2D range image)仿真了坦克的三维像。Johan C.van den Heuvel 2005年实现了舰船的激光距离像[7],并在 2009年分析了海上目标的激光距离成像[8]。
以上对于距离像的研究基本都是实验,关于距离像的理论计算模型见到的公开报道很少,瑞典军方[9]在 2008年对平板、球和圆锥的一维距离像进行了理论和实验的研究。国内关于激光距离成像的研究较少,大部分集中在激光雷达测距研究。西安电子科技大学对激光单站一维距离成像做了理论分析并进行了原理性实验研究[2,10-12]。王明军等[13]进行平板脉冲回波的实验。王彪、吴振森和宫彦军[14]研究目标表面材料特征对激光三维像影响的理论研究。
1 圆锥的二维距离像成像算法
1.1 坐标变换
激光二维散射强度像是平面波激光成的二维像,对于脉冲激光产生的二维强度像是随着脉冲波的传播而发生变化,是随时间变化的,时间对应着脉冲传播的距离,所以脉冲激光的二维散射强度像,称其为激光二维距离像,计算目标的激光二维距离像,需要计算在成像面上各个接收单元的散射强度,需要计算目标上的微元在成像面的成像单元接收的强度,设入射激光在目标坐标系下入射方向的入射天顶角为θ,入射方位角 φ,是指入射方向反方向在目标坐标下的方位角和天顶角(见图1所示)。建立成像坐标系,需要把目标坐标系变换到成像坐标系。二维散射强度像的示意图见图1所示。目标坐标系坐标 xyz,入射方向反方向为成像坐标系Z轴,成像坐标系坐标为XYZ,选择X轴、Y轴,坐标原点相同,满足如下的坐标变换。

1.2 脉冲激光雷达方程
对于一个雷达接收系统,在忽略各种损耗的情况下,雷达方程给出的接收功率表达式如下[15]:

Pt为发射机功率,K是一个与发射天线的增益、接收天线的增益、发射天线和接收接收天线与目标的距离有关的物理量,σ为目标的激光雷达散射截面[16]。当发射机功率 Pt为脉冲形式的入射功率 S(t),S(t)从光源发出,对于扩展目标,目标上每一可照射面元(x,y,z)后向散射功率如下[15]
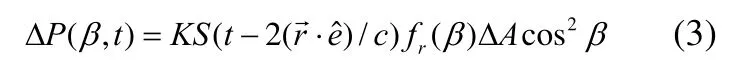
fr(β)为目标表面材料的后向双向反射分布函数,与本地入射角β和表面材料有关,当圆锥体为朗伯体时,fr(β)在圆锥上的任何微元处都相同,是常数,fr(β)=ρ/π,ρ是表面材料的半球反射率,不同的朗伯表面存在差异。Δ A为面元的面积。因为圆锥是凸体,所以对于圆锥上的点,满足cosβ>0就是可照射点。fr(β)可以测量,也可以理论建模,有的模型直接包含有面材料的介电特性、粗糙程度信息[15]。

图1 成像原理示意图
1.3 朗伯圆锥二维距离像计算模型
1.3.1 光强公式
对于朗伯表面,则式(3)变为如下的形式:
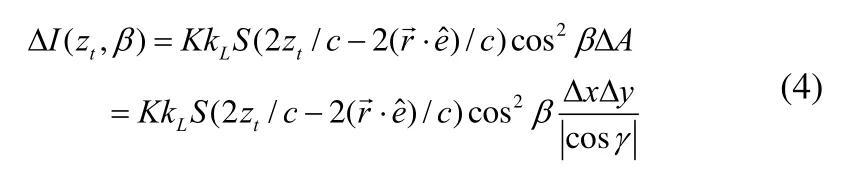
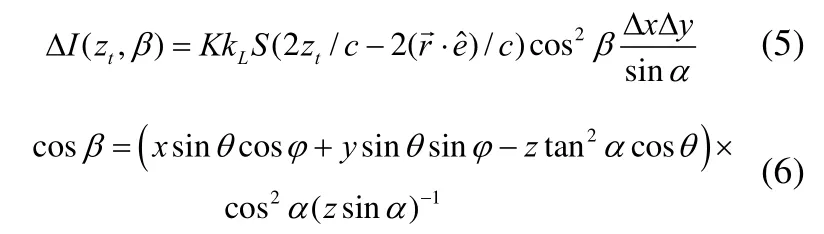
1.3.2 成像映射公式
光强公式计算出的是圆锥体表面的总光强。通过引入矩形函数可以计算出成像面上对应的成像单元的像的强度值。
矩形函数的具体表达如下:

在成像面上(XiiY)的强度如下:

Xi, Yi表示成像面上面元坐标,X,Y表示通过坐标变换变换到成像坐标系上面元的坐标。
2 仿真结果与讨论
我们根据公式(6)-(8)利用C++语言编写代码,给出朗伯圆锥的二维距离像的仿真结果。下面给出入射脉冲宽度、天顶角、圆锥的高度、圆锥的半锥角等对成像的影响。
2.1 脉冲宽度和激光入射方向的影响
图2-图4给出朗伯圆锥的高度h=0.5m,半锥角α=10o,激光入射方位角 θ=180o,脉冲宽度 T0分别为 1ns、0.5ns、0.1ns和0.01ns的二维距离像。这里ns为时间单位是纳秒,为10-9秒。

图2 h=0.5m,α=10o,θ=180o,T0=1ns的二维距离像
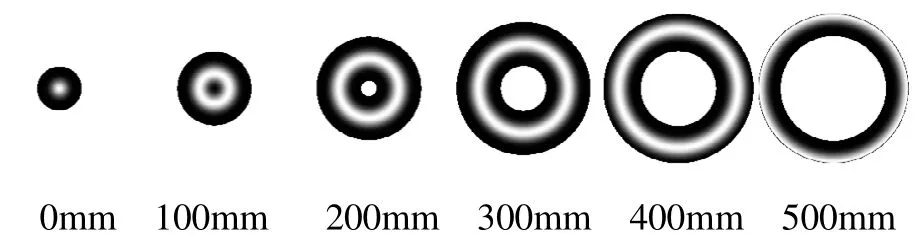
图3 h=0.5m,α=10o,θ=180o,T0=0.5ns的二维距离像
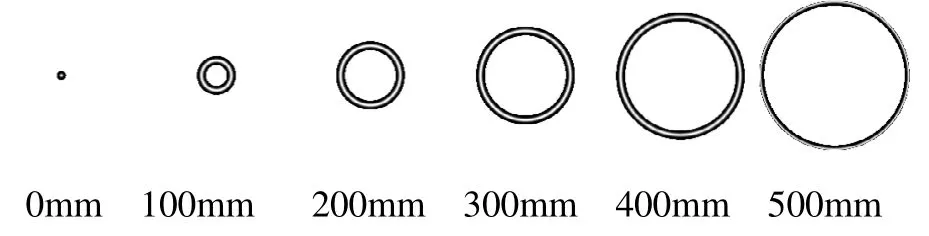
图4 h=0.5m,α=10o,θ=180o,T0=0.01ns的二维距离像
图2-图4给出的是从圆锥的尖端沿着轴的方向入射,图像是圆周对称,可以看出,随着脉冲宽度的增加,所成的二维距离像,变得越来越窄,这是因为随着脉冲宽度的减小,脉冲占据目标的单元越少,目标的成像范围变窄,因此图像越来越窄,距离分辨增加。
图5-图8给出朗伯圆锥的高度h=0.5m,半锥角α=10o,激光入射方位角θ=160o,脉冲宽度T0分别为0.01ns、0.1ns、1ns、10ns、20ns的二维距离像。

图5 h=0.5m,α=10o,θ=160o,T0=0.01ns的二维距离像

图6 h=0.5m,α=10o,θ=160o,T0=0.1ns的二维距离像

图7 h=0.5m,α=10o,θ=20o,T0=1ns的二维距离像
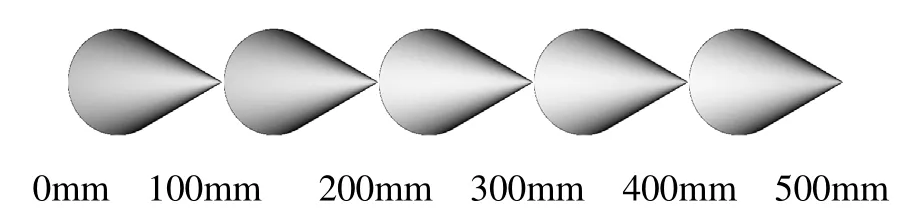
图8 h=0.5m,α=10o,θ=160o,T0=10ns的二维距离像
图5-图8给出的与前面的图2-图4的激光的入射方向不同,激光从圆锥的尖端入射,入射方向与圆锥的轴的夹角为20o,脉冲宽度从0.01ns变化到10ns,二维距离像逐渐变成二维像,这是因为随着脉冲宽度的增加,脉冲激光逐渐逼近平面波激光。
其中图5中在距离500mm处的图像数据放大了100104.9陪。其中图6中在距离500mm处的图像放数据大了2570陪。把其图形的几何尺寸放大如图9所示。从图9可以看出有2条短线。对于图5中在距离500mm处的图像,因为此时的脉冲宽度为0.01ns,很小,脉冲很窄,这时脉冲中心已经远离圆锥,覆盖在圆锥的脉冲激光的强度很小,所以成像的强度很小,其中图6中在距离500mm处的图像也很小,但比图5中在距离500mm处的图像要大,这时因为图6中的脉冲宽度是图5中10倍,相对于图5中的已经很宽了,但是和其它图的脉冲宽度比还是比较小。

图9 图5中在距离500mm处的图像的几何放大
2.2 半锥角的影响
图10给出朗伯圆锥的高度h=0.5m,半锥角α=20o,激光入射方位角θ=20o,脉冲宽度T0为0.01ns的二维距离像。其中图10中在距离500mm处的图像数据放大了6.3陪。
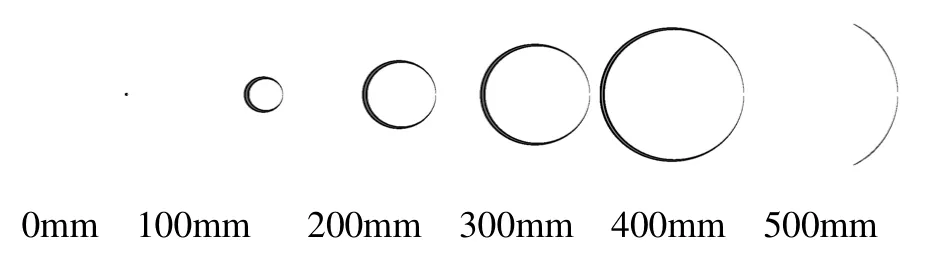
图10 h=0.5m,α=20o,θ=160o,T0=0.01ns的二维距离像
图10和图5相比只是半锥角不同,像存在差异。
2.3 高度的影响
图11给出朗伯圆锥的高度h=0.8m,半锥角α=20o,激光入射方位角θ=20o,脉冲宽度T0为0.01ns的二维距离像。
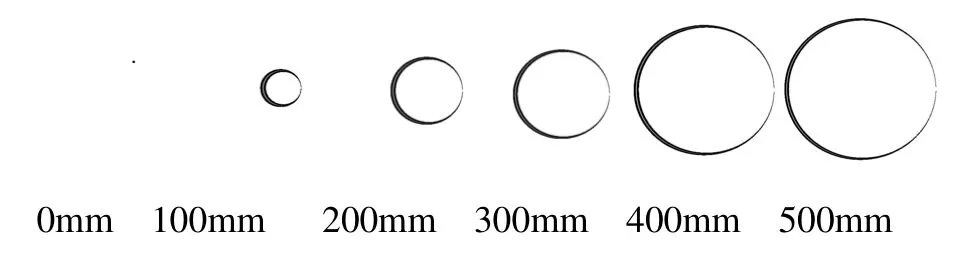
图11 h=0.8m,α=20o,θ=160o,T0=0.01ns的二维距离像
图11和图10相比,圆锥的高度增加,所以距离像距离范围增加,图11中500mm处比图10中500mm处的图像大一些。
3 结论
本文推导了朗伯二维距离像的计算公式,给出了仿真结果。分析了脉冲宽度、激光入射方向和圆锥的夹角、圆锥高度和圆锥半锥角对圆锥二维距离像的影响,随着脉冲宽度的减小,图像的距离分辨增加。随着入射方向的不同,二维距离像存在差异,能反映出目标的姿态信息。目标的高度不同,其二维距离像在距离成像上存在差异,高度越高,距离像的个数多。
[1]Donald L.Snyder.High resolution radar imaging,Washington: Washington University, 1981.
[2]陈辉.粗糙物体高斯波束散射及在激光一维距离成像中的应用[D].西安:西安电子科技大学,2004.
[3]Frederick K.Knight, David Klick, Danette P.Ryan-Howard,et al.Laser radar reflective tomography utilizing a streak camera for precise range resolution[J].APPLIED OPTICS,1989, 28(12): 2196-2198.
[4]V Galdi,DA Castaon, LB Felsen.Multifrequency reconstruction of moderately rough interfaces via quasi-ray Gaussian beams[J].IEEE Transactions on Geoscience and Remote Sensing, 2002, 40(2): 453-460.
[5]杨福民,陈婉珍.白天卫星激光测距系统的设计和实测结果[J].中国科学: A 辑, 1998, 28(011): 1048-1056.
[6]E Blanquer.LADAR proximity fuze-system study[D];Stockholm, Sweden, 2007.
[7]G.J.Kunz,H.H.P.T.Bekman,K.W.Benoist,et al.Detection of small targets in a marine environment using laser radar[J].Prco.SPIE, 2005, 5885: 58850F.
[8]J.C.Van den Heuvel, R.M.Schoemaker, R.H.M.A.Schleijpen.Identification of air and sea-surface targets with a laser range profiler[J].Prco.SPIE, 2009,7323:73230Y.
[9]O.Steinvall,L.Sj qvist,M.Henriksson,et al.High resolution ladar using time-correlated single-photon counting[J].Proc.of SPIE, 2008, 6950: 695002(1-13).
[10]Yan Hui Li,Zhen Sen Wu.Targets recognition using subnanosecond pulse laser range profiles[J].Optics Express,2010,18(16):16788-16796.
[11]李艳辉,吴振森,宫彦军,等.目标激光脉冲一维距离成像研究[J].物理学报, 2010, 59(10): 6985-6990.
[12]Yan Hui Li,Zhen Sen Wu,Yan Jun Gong.Laser range profile of the sphere[J].Proc.of SPIE, 2010, 7850: 78501J.
[13]王明军,李应乐,董群峰,等.窄脉冲激光一维高分辨回波特征实验测量[J].咸阳师范学院学报, 2010, 25(2): 19-21.
[14]B.Wang,Z.S.Wu,Y.J.Gong.Influence of surface material characteristics on laser radar 3D imaging of targets[J].Proc.of SPIE, 2010, 7855: 78551Z.
[15]宫彦军,吴振森.转动圆柱和圆锥的激光距离多普勒像分析模[J].物理学报, 2009, 58(9): 6227-6235.
[16]于文英,安里千,张志,等.朗伯圆锥激光后向二维散射成像仿真[J].湖南科技学院学报, 2012, (12): 16-19.

