ICP 加速度传感器信号失真调整方法研究❋

陈玉青，雷智强，刘会倩

（1.中北大学 机械工程与自动化学院，山西 太原 030051；2.中国人民解放军66336部队92分队，河北 高碑店 074000；3.长城汽车股份有限公司，河北 保定 071000）

0 引言

目前结构的健康状态监测与故障诊断技术越来越得到重视。能否真实地检测到足够精确的并能充分反映结构动态特性的激励信号，直接决定着后续诊断技术的使用效果及精度。在振动信号的采集过程中，经常使用到的是ICP加速度传感器。由于传感器粘合不恰当、外界环境的影响等因素，会导致采集信号的失真，有时会严重影响对信号的后续分析。在某单位的高速自动机射击实验平台上完成射击实验时，采集到的振动信号出现了失真。本文重点讨论消除加速度传感器失真的方法。

1 振动信号预处理的方法——消除趋势项

在某单位的高速自动机射击实验平台上完成射击实验时，采集到的振动信号出现了失真，如图1所示。

常用的消除趋势项的方法是多项式最小二乘法，这是一种用解析表达式来对实测数据进行数值计算拟合的算法，通过它能获得在最小平方差意义上的测试数据与数学模型的最佳拟合。最小二乘法既可以消除数字信号中的线性趋势项，又可消除非线性高阶多项式趋势项。

本文采用最小二乘法进行多项式趋势项消除，如图2所示，尝试了从2次多项式到20次多项式的多项式趋势项消除。从图2中可以看出，从9次多项式开始，才有一些明显的调整效果，但是在调整信号失真的同时也出现了波动。可见，其对此信号的失真处理效果不是很理想。

图1 采集到的失真信号和正常信号对比

2 EMD方法

EMD算法是一种信号的全新分析技术，它将信号按照时间尺度从大到小的顺序分解成多个I MF和一个余量的组合，即先分解高频再分解低频。

图3是对失真信号的EMD分解。

从图3可以看出，分量I MF1，I MF2，I MF3，I MF4是原信号的主要成分，属于原始信号的优势频段，其他的I MF是实验仪器的漂零或者信号的微弱变化趋势（见图4）。EMD作为一种新的主成分分析方法，其按照频率从高到低提取信号本身所固有的全部模态函数，并且分解出来的几个I MF分量包含了原始信号中最显著的信息，可以通过I MF的重构和余项的消除来实现信号失真的还原（见图4

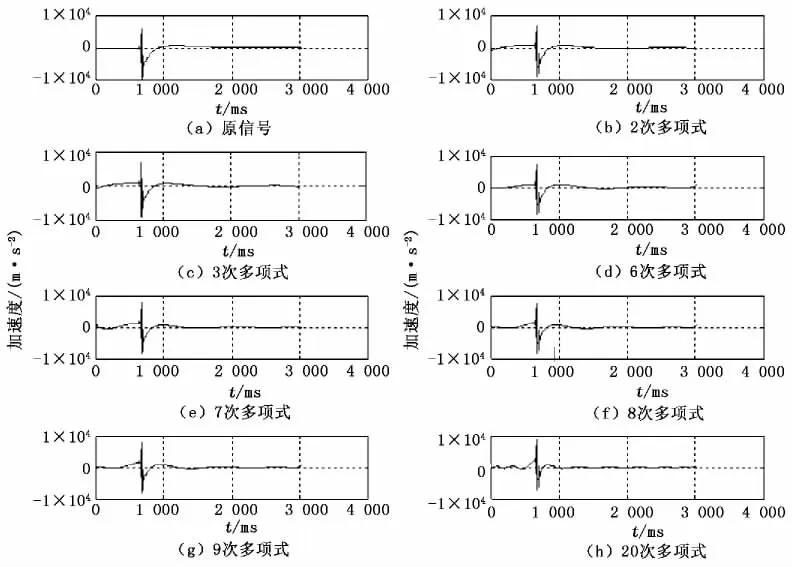
图2 多项式最小二乘法消除趋势项

图3 失真信号的EMD分解

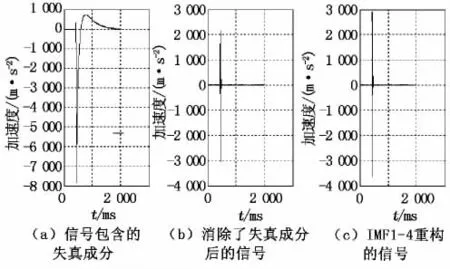
图4 消除失真后的信号

3 结束语

针对信号的失真处理，本文尝试了很多方法，最后找到了基于EMD的冲击信号的失真还原办法。从处理的效果可以看出，该方法大大提高了数据的可靠性和真实性。本文也从侧面再次验证了EMD算法应用的广泛性和有效性。

［1］张义平，李夕兵，左宇军.爆破振动信号的HHT分析与应用［M］.北京：冶金工业出版社，2008.

［2］白超，杨建慧.基于多元EMD方法的遥感图像融合［J］.激光与红外，2012，42（7）：837-840.

［3］王济，胡晓.MATLAB在振动信号处理中的应用［M］.北京：中国水利水电出版社，知识产权出版社，2006.

［4］肖立波，任建亭，杨海峰.振动信号预处理方法研究及其MATLAB实现［J］.计算机仿真，2010，27（8）：330-333.

［5］梁善勇，王江安，石晟玮，等.基于水下激光探测的高速瞬态光信号获取技术［J］.激光与红外，2008，38（6）：569-572.

［6］吴涵，冯伟杰.基于EMD的冲击信号提取方法及其在设备故障诊断中的应用［J］.现代制造工程，2001（4）：104-106.