若干基本定理的新角度证明

李玉龙

【摘要】在本科数学的教学中，高等代数和数学分析是最基本最重要的内容，其中矩阵和微积分的思想是十分绚丽且深刻的思想，能够深刻地掌握其思想精髓，灵活地运用才是目的.

【关键词】矩阵的秩定理;有限开覆盖定理;欧拉定理;可数集;隐函数组定理

然而在教学中不是一件容易的事，在本科教学中有好多学生对一些基本定理的理解显然不足，没有自己的看法和思路，甚至勉强承认书本中的逻辑式的证明，对定理的本质没有一点“感觉”，很难转化为自己的东西.为此在比较了中西方许多教科书之后，针对其中的一些基本定理，摈弃一些传统的固定模式的证明，从新角度给予阐释，目的在于把命题的本质“自然”“看得见的”呈现在读者面前，弄清楚是什么，是怎么回事，一旦明白了本质，证明只是一件简单严格叙述的事情罢了，从而帮助本科生更好地理解学习.

1.矩阵的秩定理

矩阵的行秩和列秩相等.

这是高等代数里非常基本的性质定理之一，大部分教材是通过客观的证明行秩小于等于列秩，列秩小于等于行秩来证明行秩与列秩相等.我们通过矩阵本身最基本的初等变换，给出一种自然的看法.

让我们先看看最简单的一般形式的梯形矩阵吧.

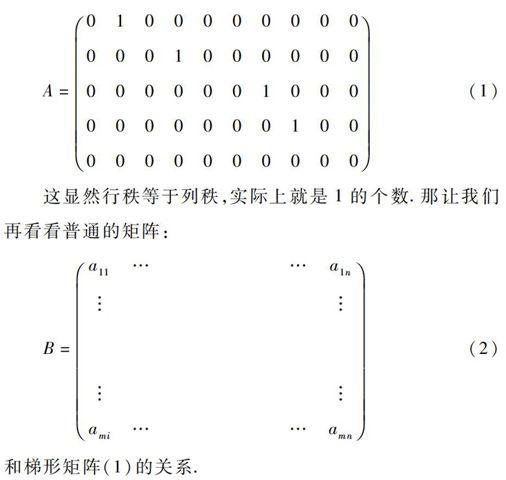
A=0100000000

0001000000

0000001000

0000000100

0000000000（1）

这显然行秩等于列秩，实际上就是1的个数.那让我们再看看普通的矩阵：

B=a11……a1n

ami……amn（2）

和梯形矩阵（1）的关系.

很显然，任何一个矩阵（2）都可以通过有限次初等变换变成（1）.

那反过来呢？因为初等变换的过程是可逆的，所以由相对应的（1）反过来可以经过有限次初等变换成原来的（2）.

因为梯形矩阵（1）的行秩与列秩是相等的，故我们只需验证初等变换不改变行秩与列秩就可以了.下面给出简单的证明.

2.有限开覆盖定理

若为闭区间上的一个开覆盖，则存在有限开覆盖.

这是数学分析教材里最基本的定理之一，也是实数完备性定理之一.实数的完备性可以说是数学中基础的基础.正确地理解实数的完备性无疑是本科生的重点和难点.但是一般的教材里的证明都让学生感觉很生涩，如果理解不到位还会让学生感觉只是逻辑的堆砌，完全看不出生活中实数的自然性，也不理解这样做的原因.大部分教材如《数学分析》（华东师范大学出版社）里的证明一般都是用分割的方法，我们考虑另一种形象的看法，然后给出一个自然的证明.

实际上我们搞清楚定理在说什么就可以了.什么是一个开覆盖？条件说存在一个开覆盖，承认存在开覆盖的同时实际上也承认了什么？

既然闭区间存在开覆盖，那当然区间里任一点都存在相应的开区间覆盖它，从而这个点和覆盖它的开区间的右边端点有个距离，比如，从点a开始，任取一个覆盖它的开区间，有个距离. 我们取所有这些距离里最大的，也就上确界，记为，如果点仍落在闭区间内，可以接着进行下去取最长的距离，依次类推.这时候只需注意到条件说存在开覆盖，也就意味着这些不断取到的点总可以超过点b（想想为什么？如果永远都到达不了点b，又怎么会有开覆盖呢？因为这已经是按照最大方式接近点b了），从而当然一定有限！也就是说实际上这些暗含的信息是等价的，搞清楚这些剩下的就是严格叙述的事了.

3.可数个可数集的并是可数集

设一组集合，若每个为可数集，则为可数集.

这个命题是实变函数教材里最基本的命题之一，关乎学生以后对分析的理解和运用.虽然很简单，但是事实是仍然有好多学生对集合论感觉很玄乎，比如选择公理之类的，以至于对这个命题也感觉可对可错.这种想法实际上是不对的.此命题是严格正确的，证明方法有很多，比如Rudin的数分析原理里的证明就是用下标标号法，实际上还可以更直接的去看待这个问题，可以“看得见的”去证明.

可数集的概念我们是用自然数集N来定义的，那就直接考虑是否和N对等就行了.下面有个很自然的看法.

4.欧拉定理

V+F-E=X（P），V是多面体P的顶点个数，F是多面体P的面数，E是多面体P的棱的条数，X（P）是多面体P的欧拉示性数.如果P可以同胚于一个球面（可以通俗地理解为能吹胀成一个球面），那么X（P）=2.特别的，P为凸多面体时，X（P）=2.

一般的教材中有很多证明，比如《整体微分几何初步》（沈一兵），用到微积分、微分形式等.针对凸多面体，下面给出一种自然的初等的看法.

【参考文献】

[1]常庚哲，史济怀.数学分析教程.第三版.高等教育出版社.

[2]王萼芳，石生明.高等代数.第三版.高等代数出版社.

[3]华东师范大学数学组.数学分析.第三版.华东师范大学出版社.

[4]Walter Rudin.The Principles Of Mathematics.Third Edition.机械工业出版社.

[5] 沈一兵.整体微分几何初步.第一版.高等教育出版社.

[6]Artin.algebra.

[7]Vladimir A.Zorich.Mathematical AnalysisI.Springer，2010（3）.

[8]Zberhard Zeidler.Applied Functional Analysis：Applications to Mathematical Physics.Spriner Third Edition.

[9]張恭庆，林源渠.泛函分析讲义.北京大学出版社，2010.