更高的交通流量,更低的交通风险,源自有效的交通规则
刘磊 徐志鹏 徐金鹏

一、背 景
在诸如中国、美国等大多数国家地区,实行靠右行驶规则.在多车道公路上,也经常要求司机靠着最右边的车道行驶,除非他们打算超车.当超车时,要从左边车道超车,之后需要再次回到原来的车道上.
尽管关于交通流量和交通风险的研究有很多,却少有研究在靠右行驶规则下,两种因子的综合影响.因此,仍然不能准确地知道一种交通规則如何影响交通情况,特别在高低负荷(车辆密度很高或很低,参考世界标准)时.与现有的靠右行驶规则相比,也许存在着更好的一种规则.
二、问题分析
调查表明,实行靠右行驶,从左超车规则的国家的比例约为66%.要了解这样一种规则的表现,需要建立一个综合评价指数来进行考量.
实际交通系统极其复杂,同时考虑所有车辆有较大困难,而考虑单辆车是方便的.因此可以从局部到整体分析,先选择一辆代表性的车进行研究,在此基础上过渡到系统研究.
在评价工程系统好坏时,比如武器装备、桥梁和房屋,常常采用安全系数进行考量.对于文中讨论的问题,可利用对应风险系数来描述.
在不同的国家,由于文化差异以及思考问题的角度影响,交通流量和风险系数在人们心中所占的权重是不一样的.因此,在分析不同国家的情况时,这样的权重影响应当被考虑.
三、模型假设与变量定义
1.模型假设
(1)在双车道中,右车道用于车辆正常行驶,左车道作为超车道(车辆只能从左车道超车).右行规则则以此为基础.
(2)天气状况良好,车道平坦且无紧急情况发生.因此,车速为正常速度且不会发生突变.
(3)每位司机的超车想法以及驾驶水平是相同的.因此,可以认为人为对车辆的影响相同.
(4)车辆间距为规定的安全车距.因此,可以根据车速来估计车辆间距.
(5)风险系数受到超车影响,且由超车视距决定.因此,RI的确定能够符合国际相关风险系数评估标准.
(6)车辆以公路设计速度进行超车.因此,可以方便地计算出修正的平均车速.
2.变量定义
vi:正常速度(m/s) a:制动加速度(m/s2)
Lio:车辆间距(m)
tr:反应时间(s,典型值:0.55 s)
tb:制动时间(s,典型值:0.56 s)
Lip:停车安全距离(m,典型值:5 m)
Di:超车视距(m)
Lv:车辆长度(m,典型值:4 m)
RIi:风险系数
vd:公路设计速度(m/s)
b,c,d:GD参量
m:超车率
ρ:车流密度(puc/km)
w:风险权重
q:交通流量
λ:相对指数
η:超车时间因子
E:综合评价指数
四、方法简介
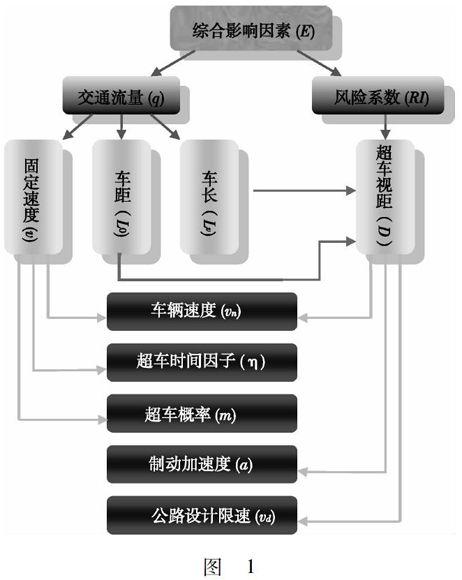
通过层次分析法,建立起相关基本模型.各层间关系如图1所示.基于这些关系,建立起流量q,风险系数RI和综合评价指标模型.原始数据来自于参考文献和相关模拟实验.基于模拟数据,对模型进一步地进行了完善,并将右行规则和自由驾驶规则进行对比.考虑到在不同的国家,流量及风险的权重是不同的,在评价指数中引入了影响因子k.
图 1
五、模型设计
1.流量模型
交通流量通常是受速度和车距影响.首先,考虑超车现象建立速度模型.由于很难找到关于超车的相关数据,故使用CA来模拟交通流和超车现象,文献[6]中的模拟数据如表1:
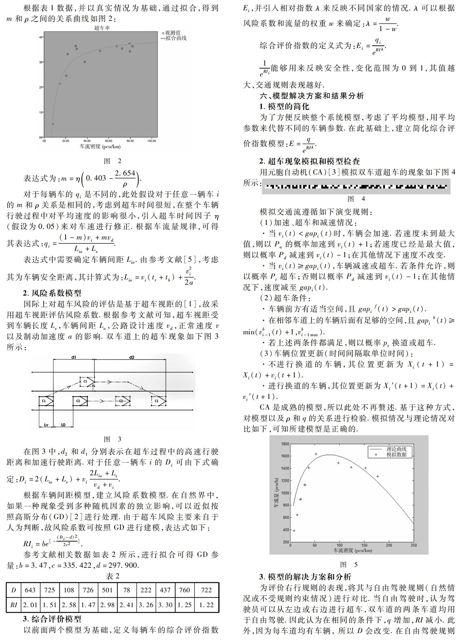
根据表1数据,并以真实情况为基础,通过拟合,得到m和ρ之间的关系曲线如图2:
图 2
表达式为:m=η0.403-2.654ρ.
对于每辆车的qi是不同的,此处假设对于任意一辆车i的m和ρ关系是相同的,考虑到超车时间很短,在整个车辆行驶过程中对平均速度的影响很小,引入超车时间因子η(假设为0.05)来对车速进行修正.根据车流量规律,可得其表达式:
qi=(1-m)vi+mvdLio+Lv.
表达式中需要确定车辆间距Lio.由参考文献[5],考虑其为车辆安全距离,其计算式为:
Lio=vi(tr+tb)+v2i2a.
2.风险系数模型
国际上对超车风险的评估是基于超车视距的[1],故采用超车视距评估风险系数.根据参考文献可知,超车视距受到车辆长度Lv,车辆间距Lo,公路设计速度vd,正常速度v以及制动加速度a的影响.双车道上的超车现象如下图3所示:
图 3
在图3中,d2和d1分别表示在超车过程中的高速行驶距离和加速行驶距离.对于任意一辆车i的Di可由下式确定:
Di=2(Lio+Lv)+vi2Lio+Lvvd+vi.
根据车辆间距模型,建立风险系数模型.在自然界中,如果一种现象受到多种随机因素的独立影响,可以近似按照高斯分布(GD)[2]进行处理.由于超车风险主要来自于人为判断,故风险系数可按照GD进行建模,表达式如下:
RIi=be[-(Di-d)22c2].
参考文献相关数据如表2所示,进行拟合可得GD参量:b=3.47,c=335.422,d=297.900.
3.综合评价模型
以前面两个模型为基础,定义每辆车的综合评价指数Ei,并引入相对指数λ来反映不同国家的情况.λ可以根据风险系数和流量的权重w来确定:
λ=w1-w.
综合评价指数的定义式为:
Ei=qieRIλ.
1eRIi能够用来反映安全性,变化范围为0到1,其值越大,交通规则表现越好.
六、模型解决方案和结果分析
1.模型的简化
为了方便反映整个系统模型,考虑了平均模型,用平均参数来代替不同的车辆参数.在此基础上,建立简化综合评价指数模型:
E=qeRIλ.
2.超车现象模拟和模型检查
用元胞自动机(CA)[3]模拟双车道超车的现象如下图4所示:
图 4
模拟交通流遵循如下演变规则:
(1)加速、超车和减速情况:
·当vi(t) ·当vi(t)≥gapi(t),车辆减速或超车.若条件允许,则以概率Pt超车;否则以概率Pd减速到vi(t)-1;在其他情况下,速度减至gapi(t). (2)超车条件: ·车辆前方有适当空间,且gapif(t)>gapi(t). ·在相邻车道上的车辆后面有足够的空间,且gapib(t)≥min(vbi-1(t)+1,vbi-1max). ·若上述两条件都满足,则以概率pt换道或超车. (3)车辆位置更新(时间间隔取单位时间): ·不进行换道的车辆,其位置更新为Xi(t+1)=Xi(t)+vi(t+1). ·进行换道的车辆,其位置更新为Xi′(t+1)=Xi(t)+vi′(t+1). CA是成熟的模型,所以此处不再赘述.基于这种方式,对模型以及ρ和q的关系进行检验.模拟情况与理论情况对比如下,可知所建模型是正确的. 图 5 3.模型的解决方案和分析 为评价右行规则的表现,将其与自由驾驶规则(自然情况或不受规则约束情况)进行对比.当自由驾驶时,认为驾驶员可以从左边或右边进行超车,双车道的两条车道均用于自由驾驶.因此认为在相同的条件下,q增加,RI减小.此外,因为每车道均有车辆, 所以D会改变.在自由驾驶规则下,双车道超车现象如图6所示: 图 6 自由驾驶规则模型为:E=qeRIλ, D=Lo+Lv+v2d-v22a,RI=1.5be-(D-d)22c2,q=1.2vLo+Lv, ρ=1000qv. 该规则与右行规则比较结果如图7(认为流量和风险指数的权重相同,所以λ是1): 图 7 根据上图可知: (1)车流密度正常,即道路处于一般负荷情况下,两种规则都合适,E处于最大值左右; (2)车流密度正常,即道路处于低负荷情况下,右行规则的表现比自由驾驶规则交通更好,且当ρ在100 pcu/km (“pcu”为车辆单位)附近时, E会达到最大值; (3)车流密度较小,即道路处于低负荷情况下,两个规则的表现是类似的且E较小; (4)车流密度很大,即道路处于高负荷情况下,右行规则表现不如自由驾驶规则. 4.改良规则 基于之前的分析,提出改良规则,目的在于改善道路高负荷或低负荷下的情况.根据右行驾驶习惯,新规则及示意图如下: ·两车道都被用于机动车道; ·右车道是慢车道,其限制速度低于普通限制速度; ·左车道是快车道且设计普通上限速度,同时增加设计速度下限; ·慢车道上的车辆可加速进入快车道,但快车道的车上不能进入慢车道; ·两条车道的限制速度之间有关联. 图 8 为建立改良规则模型,假定速度差为20公里/ 小时.根据上图,得到改善规则模型表达式: E=qeRIλ,D=Lo+Lv+v22-v212a,RI=0.8be-(D-d)22c2, q=v1(1-m)Lo+Lv+v2(1+m)L′o+Lv,ρ=1000Lo+Lv+1000L′o+Lv. 将三种规则(右行规则、自由驾驶规则、改良规则)的综合评价指数曲线对比如图9: 图 9 由上图可知,改进的规则取得了预期的效果:在高负荷和低负荷情况下E显著增加,且在正常负荷下,E增加更为显著. 5.结 论 基于以上模型,可以作如下总结: (1)右行规则很适合正常交通负载情况,而对于低负荷或高负荷却不是很适用; (2)改良规则可以提高交通流量,并且当交通系统是低负荷和高负荷时都很适用,此外,尤其适用于正常负载情况. 七、模型的改进 1.q和RI的权重 文中考虑的是交通流的权重和风险指数相同的情况,事实上在不同的国家和城市,两者对交通的整体影响是不同的.可以猜测,在发达国家和城市,人们更重视安全,风险系数权重会较大;而在发展中国家,交通是否畅通更重要,交通流的权重可能会更大.因此,当讨论不同的区域,需要分析w变化.分别改变λ为1.1和0.9来反映交通流量和风险指标权重不同的情况,前者表示发达国家或城市的情况,而后者表示发展中国家的情况.结果如下: 图 10 圖 11 可以从图中看出,在不同的地区,需要不同的交通规则. 2.多车道情况 在我们的生活中,有许多种多车道的.为了更好地使模型适应实际情况,可以考虑在双车道模型分析的基础上,进一步讨论多车道的情况. 3.CA CA通常是用于交通状况的仿真,但不是很准确的.事实上,有很多专业软件可以更准确逼真地模拟交通状况,如VISSIM,Emme和TransCAD,可以用这些软件来提高模型的准确度.

