演绎“长河落日圆”之意蕴 呈现数学教学之精彩

潘炎

《义务教育课程标准（2011年版）》指出：“教材中学习素材的选择，图片、情景、实例与活动栏目等的设置，拓展内容的编写，以及其他课程资源的利用，都应当与所安排的数学内容有实质性联系，有利于提高学生对数学实质的理解，有利于提高学生对所学内容的兴趣.”其中之义，要求数学教学必须“以学生为主体”，根据学生的认知力和兴趣点，实现对课程资源的有效整合，以提升学生的数学分析能力和文化涵养.本文以“直线与圆的位置关系”为例，通过融入人文意蕴，呈现数学教学之精彩.

一、本节课的设计理念

“大漠孤烟直，长河落日圆.”是唐朝边塞诗人王维对于黄河落日之“残红之美”的意境写照，然此种“落日之美”仅应用于语文对学生人文美感的化育略显可惜，毋庸置疑，“直线与圆的位置关系”的数学教学与“落日之美”适用性和匹配度极高，并对学生理解“直线与圆的位置关系”带来“正能量”.

在“直线与圆的位置关系”学习之前，学生对于平面几何的一些与圆相关的知识已经有所掌握，比如直线与圆的知识、圆锥曲线的知识等等，通过对这些知识的认知，学生已经能够解答一些基本的题型，对于平面几何中一些常用的解题方法也比较熟练.但基于初中生的记忆力角度来看，可能有些已经淡忘，特别是哪些比较难理解的内容更是模糊不清了.

本设计在对本堂课教学内容进行深入分析的基础上，对内容的本质与联系进行了较深的研究，同时又考虑到学生接受能力、思维发展的状况以及学生的知识基础，力求在教学过程中做到通俗易懂、自然流畅、快乐学习的效果.在教学的方法上，做到自主“探究式”教学，引导学生去发现问题、理解问题、解决问题，加强与学生之间的交流，通过现代多媒体技术，运用讲解、演示等方式來完成，在此过程中强调“教需得法”的理念，力求灵活变化.在教学目标上，注重基本的解题方法与解题基本规律的总结，以突出解析思想为主，融知识与技能、过程与方法、情感与体验为一体，力求多元价值取向.

为引起学生的好奇心，激活学生的学习兴趣，通过再现语文课本中《使至塞上》这首诗对于落日的描写，并让学生欣赏图片，让学生通过回忆、看图、分析，从而找出从圆心到切线的距离和圆的半径之间的关系，从而认识直线与圆的位置关系.此外，通过展现直线与圆的几种不同的位置关系，让学生感受运动变化的直线与圆的位置关系，培养学生运动辩证的观点.通过这些过程的呈现，学生对于直线与圆的位置关系就会得到强化和加深，有的学生甚至会把它转化到代数方程的内容之中，培养学生借助直观解决抽象问题的能力，也就是由数到形、由形到数、由直观到抽象、由抽象到直观的转化能力.

二、教学片段重现

通过回顾王维的《使至塞上》这首诗来创设一种与圆有关的意境，以此来达到激发学生兴趣的目的，通过教师与学生之间、学生与学生之间讨论，得出直线与圆的三种位置关系，即相离、相切、相交.通过一些简单的练习使学生对直线与圆的三种关系加深认识，再通过典型例题的分析，使学生的能力进一步加深，而后是课堂练习的环节，使学生学会举一反三，知识得到升华，最后是教师与学生共同归纳的环节，让学生体验本堂课给自己的愉悦感、成功感.

（一）问题情境导入

设计意图：体现“以学生为中心”的教学理念，树立起学生学习的自信心和主动性.在讲正式内容之前采用问题情境导入法，不仅加深学生的印象，还激发学生的热情.

为了激发学生的好奇心，提高学生学习的热情，本堂课将围绕主题引用学生非常熟悉的王维的《使至塞上》里面的“大漠孤烟直，长河落日圆”作为情景导入，并让学生欣赏图片.具体过程如下：

师：同学们，大家还记得唐代诗人王维的《使至塞上》这首诗吗？里面有一句名句：大漠孤烟直……

生：长河落日圆.

师：很好！大家能不能简单地描绘一下“长河落日圆”的画面呢？

生：太阳在河面上缓缓落下.

师：这幅画便是“长河落日圆”的写照，给我们展现了黄河映衬着落日的残红之美.

师：在数学中，我们可以把远处横卧的长河视为一条……

生：直线.

师：临近河面逐渐下沉的一轮落日可以被看作是一个……

生：圆.

师：那么，当落日逐渐下落的时候，这个“圆”与“直线”的交点的个数会出现几种不同的情形呢？

生：有3种.

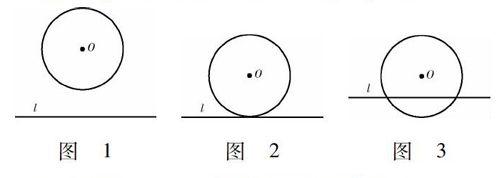
师：分别是怎样的3种？能画出草图吗？

图 1 图 2 图 3

（二）揭示课题——直线与圆的位置关系

问题：在前面课堂的学习中，我们已经掌握了关于直线的方程和圆的方程，那当我们讲到直线与圆的位置关系时，能否也用方程来表示呢？如果可以的话，又该如何表示呢？

设计意图：从已有的知识经验出发，建立新旧知识之间的联系，构建学生学习的最近发展区，不断加深对问题的理解.

（三）直线与圆的位置关系的判断

问题：方法一是用平面几何知识判断直线与圆的位置关系，你能根据直线与圆的方程判断它们之间的位置关系吗？

设计意图：引导学生用直线与圆的方程判断直线与圆的位置关系，体验坐标法的思想方法.

问题：这是利用圆心到直线的距离d与半径r的大小关系判断直线与圆的位置关系.请问用这种方法的一般步骤如何？

设计意图：对判断直线与圆的位置关系步骤进行小结，对知识进行梳理，使学生有“操作规范”，培养归纳能力，同时也渗透了算法思想.

三、教学的思考与感悟

（一）转变观念，培养学生的“参与意识”

数学家毕达哥拉斯曾经说过：“在数学的天地里，重要的不是我们知道什么，而是我们怎么知道什么.”“知道什么”指的是知识的含量，而“怎么知道什么”指的是获得知识的方法，众所周知，知识是不断地更新的，然获得知识的方法却能在知识更新的过程中发挥重要效能.实际上，通过何种教学方法来推动学生获取知识，并实现“举一反三”正是数学教学的核心所在.本堂课正是从系统论的角度着手，建立起人文知识与数学知识的逻辑联系，让学生在已有知识的储备下，更容易理解“直线与圆的位置关系”.首先在导入环节让学生感受“大漠孤烟直，长河落日圆”的人文意境，为学生了解直线与圆相切、相交、相离的几种关系从语文角度进行引入.其次是开展探究性教学，从学生的最近发展区出发，通过问题的设置，让学生层层深入地探究直线与圆的位置关系.最后是坚持以学生为主体，对本堂课的教学目标比较明确，采用“以学生为主体”的教学理念，对教学活动的过程进行了精心的设计.在教学过程中，实现了教师与学生之间的互动交流，充分挖掘学生的潜力，充分运用现代多媒体技术，提高学生课堂参与度，提升了教学效果.

（二）灵光闪现，激活学生的“探究意识”

康托尔说过：“数学的本质在于它的自由.”开展有益的课堂探究是实现数学自由的外在表现，本堂课在教学设计中充分表达了探究性教学的理念，让学生能够“伸一伸手”“动一动脑”便能获取知识.比如，在探究“直线与圆之间的位置关系”时，教师让学生根据落日之美的意境画出来，这时学生便可以从平时对落日的观察中，了解相交、相离、相切这三种关系.苏霍姆林斯基说过：“真正的教育智慧在于教师保护学生的表现力和创造力，经常激发他们体验学习快乐的愿望.”在教师所营造的探究性教学氛围下，学生的表现力和创造力得到了显示的机会，画出了草图，建构起新旧知识的关系.

《新课标（2011年版）》指出：“课程内容要反映社会的需要、数学的特点，要符合学生的认知规律.”本堂课的教学设计正是切合了这一点，从学生的原有知识结构出发，从“学生已经知道了什么”这一影响教学的最重要因素出发，并以此来开展教学，避免了以往课堂教学“僵尸化”“刻板化”，并从系统论的角度，重构课堂，给学生以新鲜的学习体验，实现快乐教学、快乐学习，进而提升教学的效果.

【参考文献】

[1]中华人民共和国教育部制定.义务教育数学课程标准（2011年版）[M].北京：北京师范大学出版社，2012.

[2]余莉，陈志华.“以学定教”的教学课例与评析——以“直线与圆的位置关系”为例[J].数学学习与研究，2013（4）.

[3]杨晓彬， 王磊.基于系统思维下的课堂教学再塑——“探索三角形相似的条件”教学设计的重组与反思[J].中学数学（初中版），2014（2）.