牛顿第二定律为什么不写成而是F＝ma

霍良平

（旬阳中学，陕西 旬阳 725700）

牛顿第二定律是研究质点在合力作用下，其运动状态如何变化的问题.在大学物理教程和高中物理教材中都是以实验为基础总结出的实验结论，对研究力和运动起到了决定性的作用，由于在高中教材中对牛顿第二定律的推导过程主要是在实验的基础上以国际单位为主线得出结论或F∝ma，而在具体的做题当中都是以F∝ma的形式出现，不写成的原因究竟是为什么？本文结合大学物理教程和高中物理教材做一比对分析.

大学教程［1］中：设质量为m的质点M，某时刻的速度为v，动量为mv，某时刻质点动量对时间的变化率等于该时刻作用在质点上所有力的合力R＝∑iFi实验表明：

牛顿第二定律给出了力和动量变化之间的定量关系.当质点的质量可以看做是常量时，上式可写为

这就是大家熟悉的牛顿第二定律的表示形式.实验表明，当质点的质量随时间变化时，式（2）已不再成立，但式（1）仍然成立，说明用动量形式表示的牛顿第二定律具有更大的普遍性.

高中教材［2］中：分别采用控制质量和力的前提下，通过实验探究加速度与力、质量的关系，得出实验结论：物体的加速度跟受到的作用力成正比，跟物体的质量成反比.数学公式表示为

将上式写成等式，得

式中的k是比例系数，取国际单位（规定1N是使质量为1kg的物体产生1m／s2加速度的力），k＝1，上式可写为F合＝ma.

（1）从单位制角度讲，最早物理学中使质量为1kg的物体产生1m／s2的加速度所需要的力叫做千克力，后来将千克力改用为牛，即使质量为1kg的物体产生1m／s2的加速度所需要的力为1牛.从单位分类来看牛是导出单位，可表示为1N＝1kg·m／s2，因此将牛顿第二定律表示为F＝ma体现了单位的导出过程.

（3）牛顿第二定律的内容当中并没有具体要求研究对象只能为一个质量一定的物体或加速度相同的物体系，即可理解为对变质量的物体、加速度不同的多个物体系也应在它的研究范围内.

设有n个相互作用的物体质量一定，分别为m1、m2、..mn，产生的加速度分别为a1、a2、..an，m1受到的作用力分为F1内（m2，..mn对m1施加的力的合力）、F1外（除m2，..mn对m1施加力之外的力的合力），同理m2受到的作用力分为F2内、F2外，mn受到的作用力分为Fn内、Fn外.根据牛顿第二定律得

F1外＋F1内＝m1a1. （1）

F2外＋F2内＝m2a2. （2）

……

Fn外＋Fn内＝mnan. （n）

据牛顿第三定律得F1内＋F2内＋…＋Fn内＝0，则式（1）＋式（2）＋…＋式（n）得

F1外＋F2外＋…＋Fn外＝m1a1＋m2a2＋…＋mnan.

如果取m1，m2，…mn系统为研究对象，有

F合外＝m1a1＋m2a2＋…＋mnan.

结合力的正交分解思想，上式可写为

Fx＝m1a1x＋m2a2x＋…＋mnanx，

Fy＝m1a1y＋m2a2y＋…＋mnany，

式中的Fx和Fy是系统在x轴、y轴方向上的合外力.若牛顿第二定律写成将无法列出系统的牛顿第二定律方程，即只能局限于解决单个物体或可视为单体的多个物体系（加速度相同）的力学问题，在学生应用牛顿第二定律解决力学问题时存在很大的局限性，甚至会使学生曲解为牛顿第二定律只能解决单体定质量问题.

例题.一个斜面光滑质量为M的三角劈放在粗糙的地面上，一个质量为m的滑块从斜面顶端静止释放，在滑块的下滑过程中，三角劈始终不动，那么三角劈所受地面的摩擦力的大小和方向怎样？支持力又有多大？

解析：分别以三角劈和滑块为研究对象作受力分析，如图2（a）、（b）所示.

图1

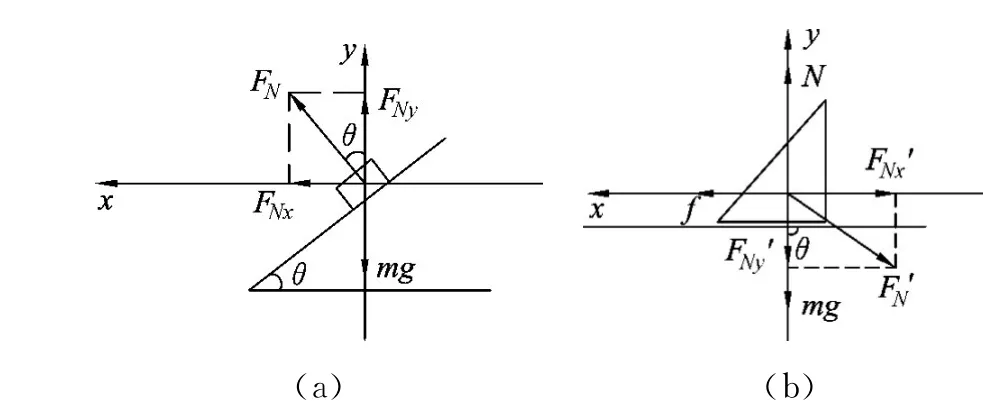
图2

x轴方向：当M和m一定时，取水平向左为正方向，滑块的加速度为a1＝gsinθ，三角劈的加速度为a2＝0.

对滑块：

FNx＝FNsinθ＝ma1x. （1）

对三角劈：

f-FN′sinθ＝Ma2x. （2）

y轴方向：取竖直向下为正方向.

对滑块：

mg-FNcosθ＝ma1y. （3）

对三角劈：

Mg＋FN′cosθ-N＝Ma2y. （4）

FN＝FN′.（数值相等） （5）

如果采用单体分析法，先有（1）式算出FN＝mgcosθ，代入（2）式得出f＝mgsinθcosθ，代入（4）式得出

N＝（M＋m）g-mgsin2θ.

系统分析法.

x轴方向：f＝ma1x＋Ma2x.

y轴方向：mg＋Mg-N＝ma1y＋Ma2y.于是直接可得f＝mgsinθcosθ，且方向水平向左，N＝（M＋m）g-mgsin2θ.

1 吴百诗.大学物理（新版）［M］.北京：科学出版社，2001.

2 束炳如，何润伟.物理（共同必修1）［M］.上海：上海科技出版社，2004.